CSI 312 Computer Organization Lecture 6 Logic Arithmetic

CSI 312 - Computer Organization Lecture 6 - Logic & Arithmetic 2011 Homework: p: 229: 3. 1, 3. 2, 3. 3, 3. 4, 3. 5, 3. 6 p: 231: 3. 27 ORACLE Arithmetic Unit Image Source: Oak Ridge National Laboratory

Roadmap for the Term: Major Topics 4 Computer Systems Overview 4 Technology Trends 4 Instruction Sets (and Software) 4 Logic and Arithmetic 3 4 Performance 4 Processor Implementation 4 Memory Systems 4 Input/Output Lecture 6 - Logic & Arithmetic 2

Arithmetic & Logic Unit 4 Perform the calculations 4 Everything else in the computer is there to serve this unit 4 Handles integers 4 May handle floating point numbers 4 May be separate (math co-processor) 3

Outline - Logic & Arithmetic 4 Review: Numbers & Arithmetic 3 4 Positional Number Systems 4 Signed Number Representation 4 Review: Addition & Subtraction 4 ALU Design Lecture 6 - Logic & Arithmetic 4

Review: Positional Notation of Numbers 4 Example: Binary (base 2) numbers 4 Base = 2 4 Digits = {0, 1} Note “bit” == “Binary digit” 4 N = 1001 two = 1 X 20 + 0 X 21 + 0 X 22 + 1 X 23 = 1 ten + 8 ten = 9 ten 4 Example: Hexadecimal (base 16) numbers 4 Base = 16 4 Digits = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} 4 N = 1 A 3 Fhex = 15 X 160 + 3 X 161 + 10 X 162 + 1 X 163 = 15 ten + 48 ten + 2560 ten + 4096 ten = 6719 ten = 0001101000111111 two Lecture 6 - Logic & Arithmetic 5

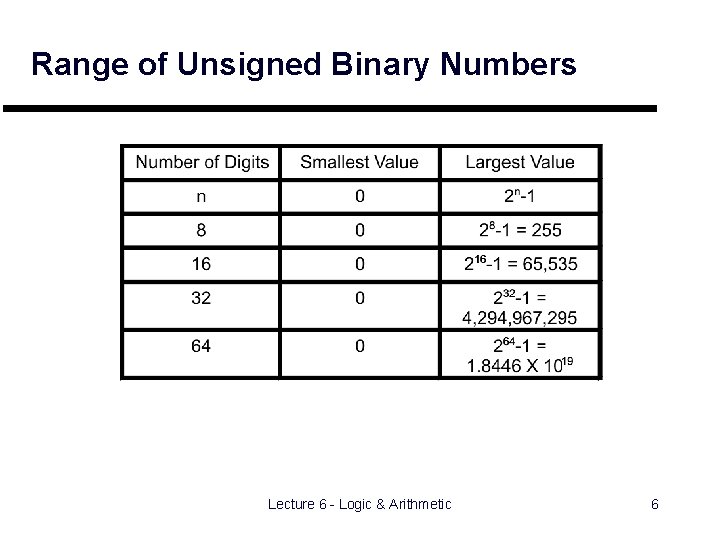
Range of Unsigned Binary Numbers Lecture 6 - Logic & Arithmetic 6

Review: Unsigned vs. Signed Numbers 4 Basic binary - allows representation of non-negative numbers only In C, Java, etc: unsigned int x; Useful for unsigned quantities like addresses 4 Most of us need negative numbers, too! In C, Java, etc: int x; How can we do this? … Use a signed representation Lecture 6 - Logic & Arithmetic 7

Signed Number Representations 4 Sign/Magnitude 4 Two’s Complement - the one almost everyone uses 4 One’s Complement 4 Biased - used for exponent sign in Floating Point Lecture 6 - Logic & Arithmetic 8

Sign/Magnitude Representation 4 Approach: Use binary number and added sign bit 1 0 0 1 Sign Magnitude = -25 4 Problems: 4 Two values of zero 4 Difficult to implement in hardware - consider addition • Must first check signs of operands • Then compute value • Then compute sign of result Lecture 6 - Logic & Arithmetic 9

Two’s Complement Representation 4 Goal: make the hardware easy to design 4 Approach: explicitly represent result of “borrow” in subtract 4 Borrow results in “leading 1’s” 4 Weight leftmost “sign bit” with -2 n-1 4 Use sign bit to represent “last borrow” N = 1111 tc = 1 X 20 + 1 X 21 + 1 X 22 + 1 X-23 = 7 ten + -8 ten = -1 ten N = 1001 tc = 1 X 20 + 0 X 21 + 0 X 22 + 1 X-23 = 1 ten + -8 ten = -7 ten N = 0101 tc = 1 X 20 + 0 X 21 + 1 X 22 + 0 X-23 = 1 ten + 4 ten = 5 ten 4 All negative numbers have a “ 1” in the sign bit 4 Single representation of zero Lecture 6 - Logic & Arithmetic 10

Range of Two’s Complement Numbers Lecture 6 - Logic & Arithmetic 11

Negating Two’s Complement Numbers 4 Important shortcut 4 Invert the individual bits 4 Add 1 4 Result: two’s complement representation of negated number! 4 Examples (with 4 bits): - (0111) = 1000+1 = 1001 -7 - (1100) = 0011+1 = 0100 +4 - (1111) = 0000+1 = 0001 +1 Lecture 6 - Logic & Arithmetic 12

Other Signed Binary Representations 4 One’s Complement 4 Use one’s complement (inverted bits) to represent negated numbers +1 = 0001 -1 = Invert(0001) = 1110 4 Problem: two values of zero (0000, 1111) Lecture 6 - Logic & Arithmetic 13

Sign Extension 4 To convert a “narrower” signed number to a “wider” one: 4 Copy the bits of the narrower number into the lower bits 4 Copy the sign bit from the narrower number into all of the remaining bits of the result 4 Example: Converting signed 8 -bit byte to 32 -bit word: 11111010 Orignal byte: -6 111111111111010 Result word: -6 00101011 Orignal byte: 45 000000000000 00101011 Result word: 45 Lecture 6 - Logic & Arithmetic 14

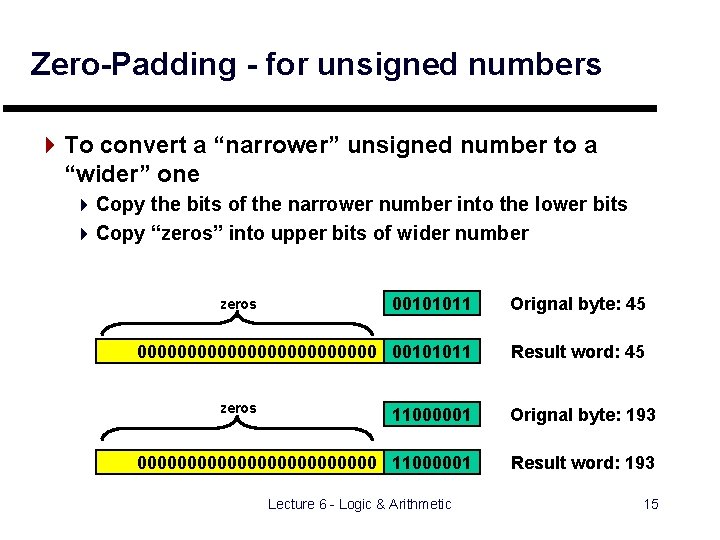
Zero-Padding - for unsigned numbers 4 To convert a “narrower” unsigned number to a “wider” one 4 Copy the bits of the narrower number into the lower bits 4 Copy “zeros” into upper bits of wider number 00101011 Orignal byte: 45 000000000000 00101011 Result word: 45 zeros 11000001 Orignal byte: 193 000000000000 11000001 Result word: 193 Lecture 6 - Logic & Arithmetic 15

Sign Extension in MIPS 4 Load-byte (lb) instruction 4 Loads an 8 -bit signed number from memory 4 Performs sign extension before placing in 32 -bit register 4 Load-byte unsigned (lbu) 4 Loads an 8 -bit unsigned number (e. g. , ASCII character) from memory 4 No sign extension - places byte with leading “ 0’s” in 32 -bit register Lecture 6 - Logic & Arithmetic 16

Sign Extension in MIPS I-Format Instructions 4 I-Format Instructions have 16 -bit immediate field 4 MIPS operations are defined on 32 -bit registers 4 Sign extension performed on immediate operands “when it makes sense” 4 Sign extension used for addi, beq, bne, . . . 4 Zero-padding used for andi, ori, . . . Lecture 6 - Logic & Arithmetic 17

Outline - Logic & Arithmetic 4 Review: Numbers & Arithmetic 4 Positional Number Systems 4 Signed Number Representation 4 Review: Addition & Subtraction 3 4 Carry Lookahead: Making Addition Fast 4 ALU Design 4 Shifters 4 Summary Lecture 6 - Logic & Arithmetic 18

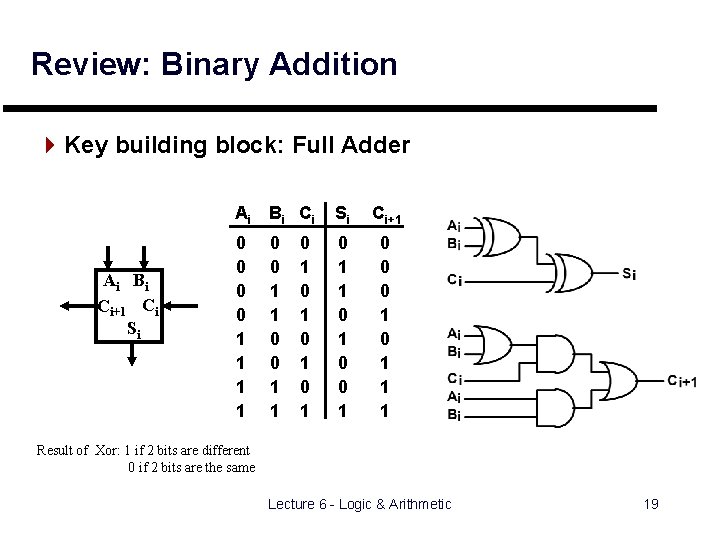
Review: Binary Addition 4 Key building block: Full Adder Ai B i Ci+1 Ci Si Ai Bi Ci Si Ci+1 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 1 1 0 1 0 1 Result of Xor: 1 if 2 bits are different 0 if 2 bits are the same Lecture 6 - Logic & Arithmetic 19

Binary Arithmetic ° Add up to 3 bits at a time per place value • A and B • “carry in” ° Output 2 bits at a time carry-in bits A bits B bits + sum bits carry-out bits • sum bit for that place value 1 1 0 0 1 0 1 1 1 0 B A • “carry out” bit (becomes carry-in of next bit) ° Can be done using a function with 3 inputs, 2 outputs 1 carry out FA sum carry in

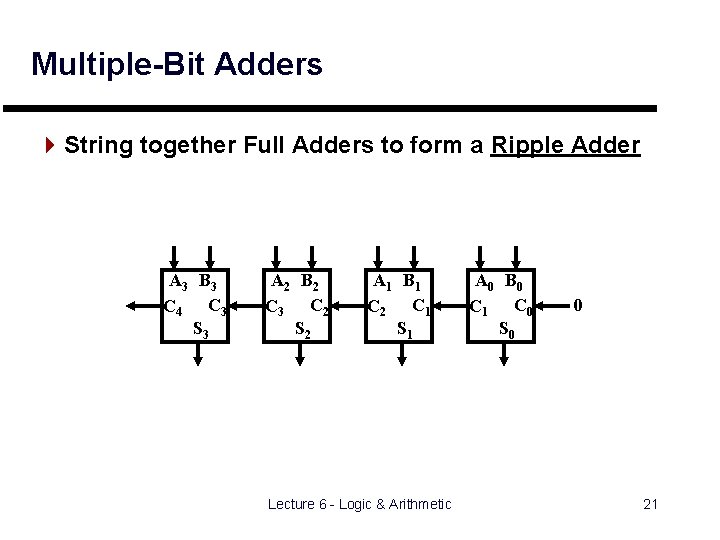
Multiple-Bit Adders 4 String together Full Adders to form a Ripple Adder A 3 B 3 C 4 C 3 S 3 A 2 B 2 C 3 C 2 S 2 A 1 B 1 C 2 C 1 S 1 Lecture 6 - Logic & Arithmetic A 0 B 0 C 1 C 0 S 0 0 21

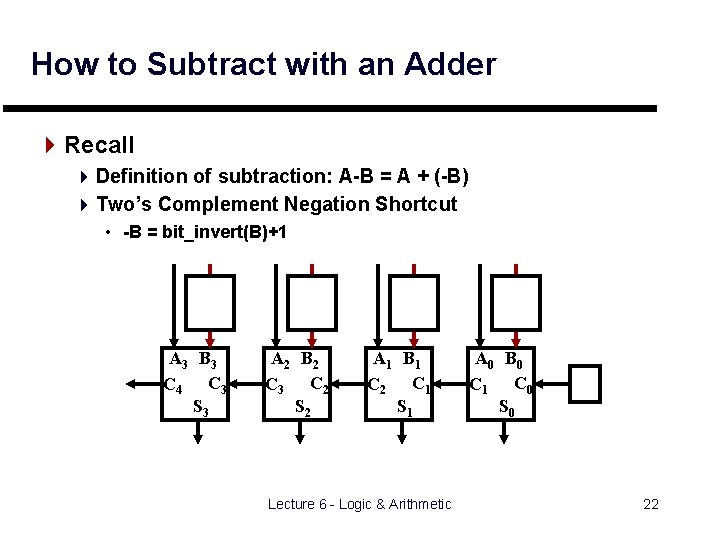
How to Subtract with an Adder 4 Recall 4 Definition of subtraction: A-B = A + (-B) 4 Two’s Complement Negation Shortcut • -B = bit_invert(B)+1 A 3 B 3 C 4 C 3 S 3 A 2 B 2 C 3 C 2 S 2 A 1 B 1 C 2 C 1 S 1 Lecture 6 - Logic & Arithmetic A 0 B 0 C 1 C 0 S 0 1 22

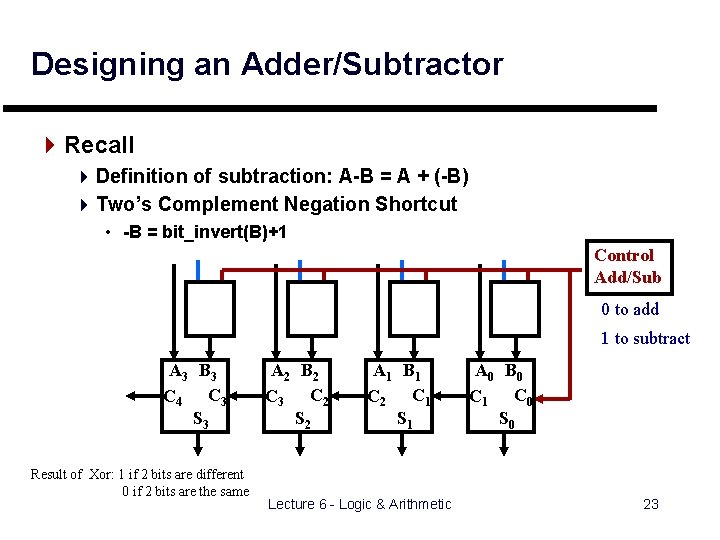
Designing an Adder/Subtractor 4 Recall 4 Definition of subtraction: A-B = A + (-B) 4 Two’s Complement Negation Shortcut • -B = bit_invert(B)+1 Control Add/Sub 0 to add 1 to subtract A 3 B 3 C 4 C 3 S 3 Result of Xor: 1 if 2 bits are different 0 if 2 bits are the same A 2 B 2 C 3 C 2 S 2 A 1 B 1 C 2 C 1 S 1 Lecture 6 - Logic & Arithmetic A 0 B 0 C 1 C 0 S 0 23

Overflow in addition & subtraction 4 Overflow - occurs when not enough bits are available to represent the result 4 Example: unsigned 32 -bit result ≥ 232 4 Example: signed 32 -bit result < -231 or ≥ 231 4 Detecting overflow - look for different signs in operands vs. result: Operation Operand A Operand B Result A+B ≥ 0 <0 A+B <0 <0 ≥ 0 A-B ≥ 0 <0 <0 A-B <0 ≥ 0 Lecture 6 - Logic & Arithmetic 24

What to do when overflow occurs? 4 In some languages (e. g. , C, Java) - nothing (“responsibility left to the programmer”) 4 In other languages (e. g. Ada, Fortran) - “notify programmer” through runtime exception 4 How MIPS handles overflow: 4 add, sub, addi - runtime exception on overflow 4 addu, subu, addiu - no runtime exception on overflow Lecture 6 - Logic & Arithmetic 25

Outline - Logic & Arithmetic 4 Review: Numbers & Arithmetic 4 Positional Number Systems 4 Signed Number Representation 4 Review: Addition & Subtraction 4 Carry Lookahead: Making Addition Fast 4 ALU Design 3 4 Shifters 4 Summary Lecture 6 - Logic & Arithmetic 26

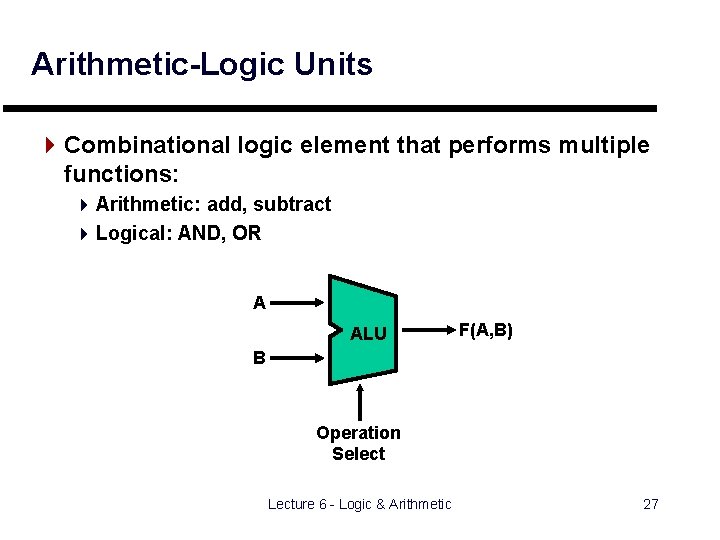
Arithmetic-Logic Units 4 Combinational logic element that performs multiple functions: 4 Arithmetic: add, subtract 4 Logical: AND, OR A ALU F(A, B) B Operation Select Lecture 6 - Logic & Arithmetic 27

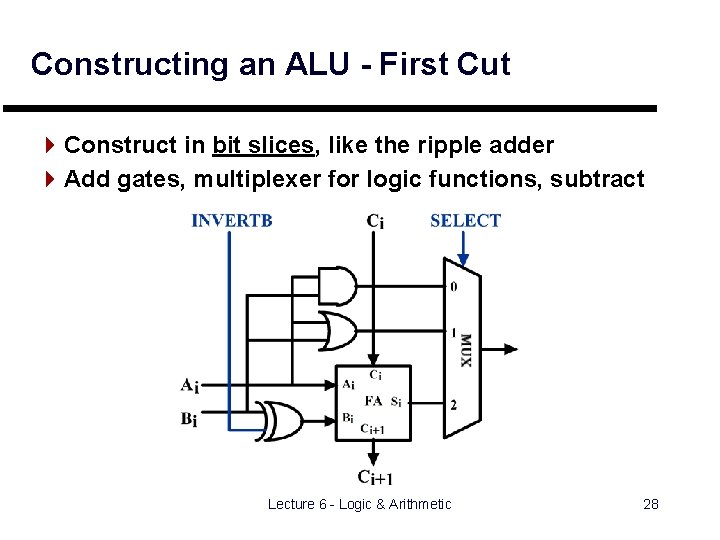
Constructing an ALU - First Cut 4 Construct in bit slices, like the ripple adder 4 Add gates, multiplexer for logic functions, subtract Lecture 6 - Logic & Arithmetic 28

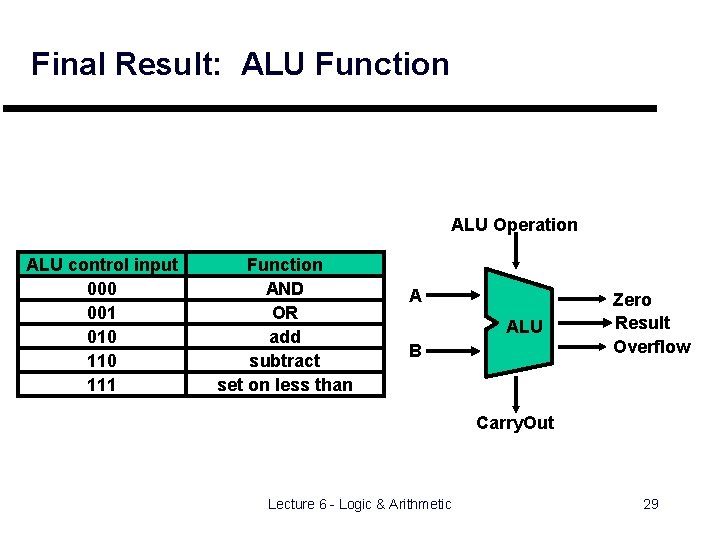
Final Result: ALU Function ALU Operation ALU control input 000 001 010 111 Function AND OR add subtract set on less than A ALU B Zero Result Overflow Carry. Out Lecture 6 - Logic & Arithmetic 29

Outline - Multiplication and Division 4 Multiplication 4 Review: Shift & Add Multiplication 4 Review: Booth’s Algorithm 4 Combinational Multiplication 4 MIPS Multiplication Instructions 3 4 Division 4 Summary Lecture 8 - Mult. & Division 30

Multiplication 4 Basic algorithm analogous to decimal multiplication 4 Break multiplier into digits 4 Multiply one digit at a time; shift multiplicand to form partial products 4 Create product as sum of partial products Multiplicand Multiplier Product 0110 X 0011 0110 0000 00010010 (6) (3) Partial Products (18) 4 n bit multiplicand X m bit multiplier = (n+m) bit product Lecture 8 - Mult. & Division 31

Multiplier Hardware 4 Sequential 4 Combinational Lecture 8 - Mult. & Division 32

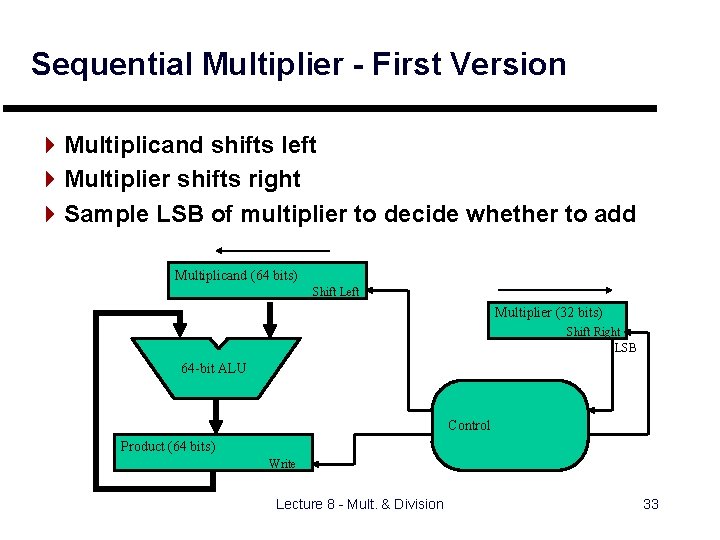
Sequential Multiplier - First Version 4 Multiplicand shifts left 4 Multiplier shifts right 4 Sample LSB of multiplier to decide whether to add Multiplicand (64 bits) Shift Left Multiplier (32 bits) Shift Right LSB 64 -bit ALU Control Product (64 bits) Write Lecture 8 - Mult. & Division 33

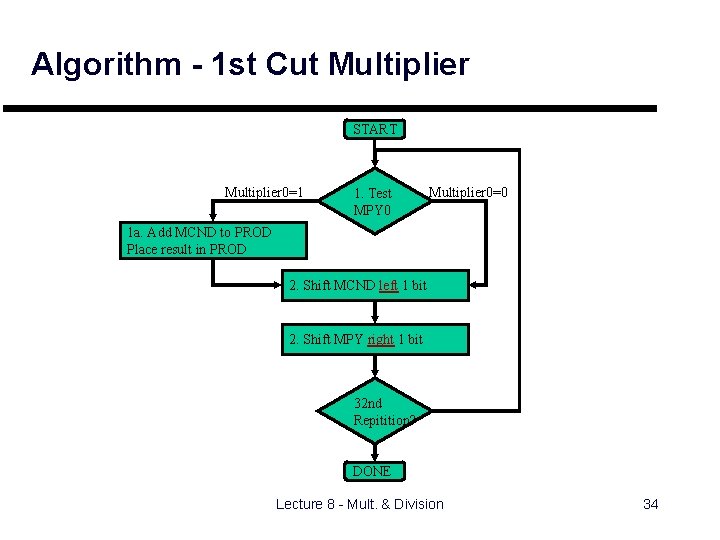
Algorithm - 1 st Cut Multiplier START Multiplier 0=1 1. Test MPY 0 Multiplier 0=0 1 a. Add MCND to PROD Place result in PROD 2. Shift MCND left 1 bit 2. Shift MPY right 1 bit 32 nd Repitition? DONE Lecture 8 - Mult. & Division 34

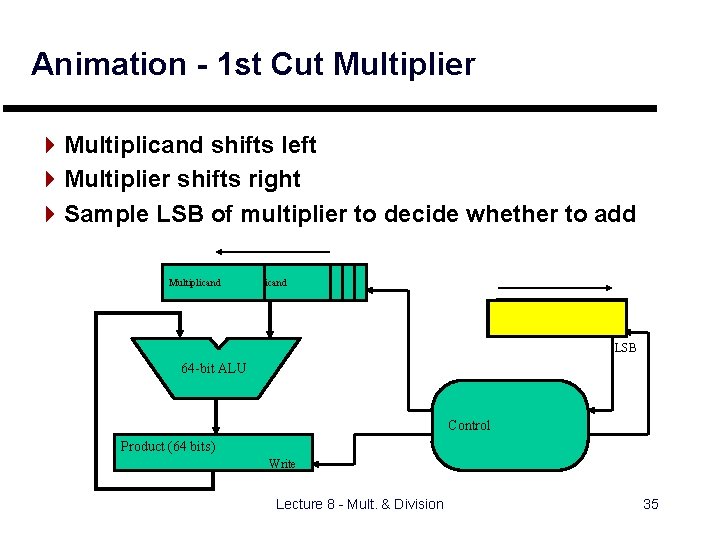
Animation - 1 st Cut Multiplier 4 Multiplicand shifts left 4 Multiplier shifts right 4 Sample LSB of multiplier to decide whether to add Multiplicand Multiplicand Multiplier LSB 64 -bit ALU Control Product (64 bits) Write Lecture 8 - Mult. & Division 35

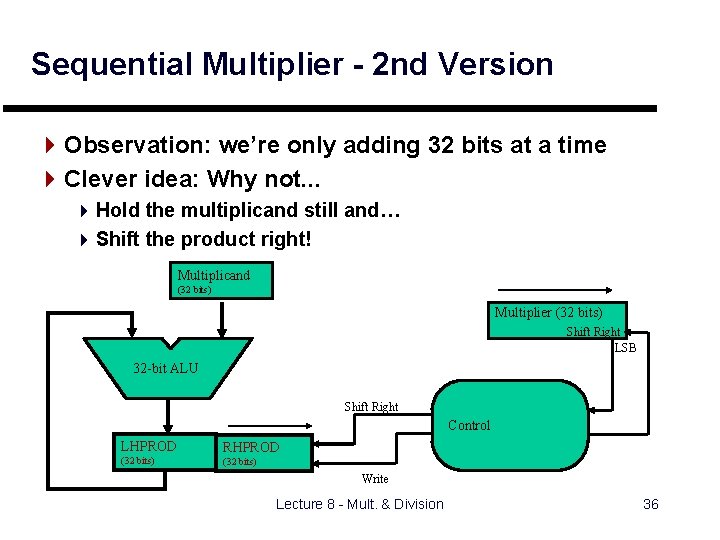
Sequential Multiplier - 2 nd Version 4 Observation: we’re only adding 32 bits at a time 4 Clever idea: Why not. . . 4 Hold the multiplicand still and… 4 Shift the product right! Multiplicand (32 bits) Multiplier (32 bits) Shift Right LSB 32 -bit ALU Shift Right Control LHPROD Product RHPROD (32 (64 bits) (32 bits) Write Lecture 8 - Mult. & Division 36

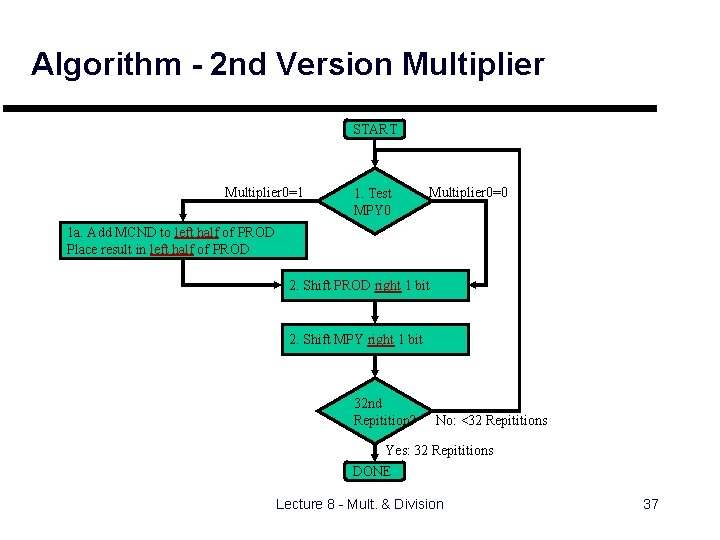
Algorithm - 2 nd Version Multiplier START Multiplier 0=1 1. Test MPY 0 Multiplier 0=0 1 a. Add MCND to left half of PROD Place result in left half of PROD 2. Shift PROD right 1 bit 2. Shift MPY right 1 bit 32 nd Repitition? No: <32 Repititions Yes: 32 Repititions DONE Lecture 8 - Mult. & Division 37

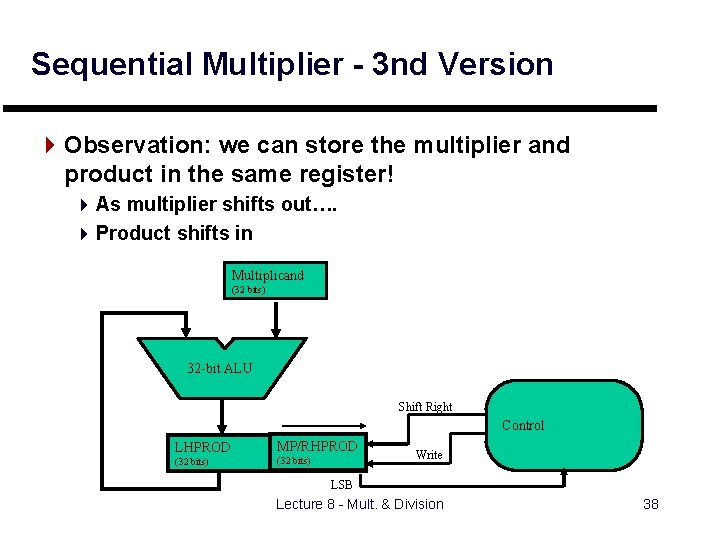
Sequential Multiplier - 3 nd Version 4 Observation: we can store the multiplier and product in the same register! 4 As multiplier shifts out…. 4 Product shifts in Multiplicand (32 bits) 32 -bit ALU Shift Right Control Product LHPROD MP/RHPROD MPY (initial) (64 bits) (32 bits) Write LSB Lecture 8 - Mult. & Division 38

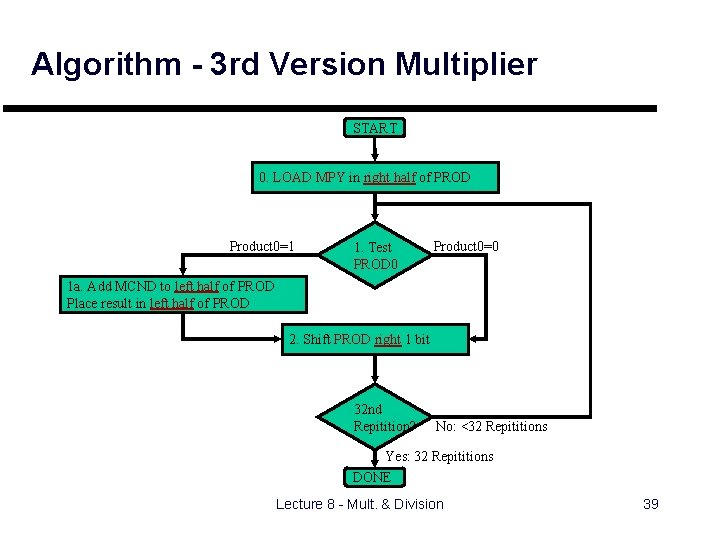
Algorithm - 3 rd Version Multiplier START 0. LOAD MPY in right half of PROD Product 0=1 1. Test PROD 0 Product 0=0 1 a. Add MCND to left half of PROD Place result in left half of PROD 2. Shift PROD right 1 bit 32 nd Repitition? No: <32 Repititions Yes: 32 Repititions DONE Lecture 8 - Mult. & Division 39

Outline - Multiplication and Division 4 Multiplication 4 Review: Shift & Add Multiplication 4 Review: Booth’s Algorithm 3 4 MIPS Multiplication Instructions 4 Division 4 Summary Lecture 8 - Mult. & Division 40

Signed Multiplication with Booth’s Algorithm 4 Originally proposed to reduce addition steps 4 Bonus: works for two’s complement numbers 4 Multiply negative numbers 4 Uses shifting, addition, and subtraction Lecture 8 - Mult. & Division 41

Booth’s Algorithm 4 Observation: if we can both add and subtract, there are multiple ways to create a product 4 Example: multiply 2 ten by 6 ten (0010 two X 0110 two) 4 Product = (2 X 2) + (2 X 4) OR 4 Product = (2 X -2) + (2 X 8) Regular Algorithm X + + 0010 0110 0000 0010 00001100 Booth’s Algorithm X shift + add shift + 0010 0110 0000 0010 00001100 Lecture 8 - Mult. & Division shift + subtract shift + add 42

Booth’s Algorithm Continued 4 Question: 4 How do we know when to subtract? 4 When do we know when to add? 4 Answer: look for “runs of 1 s” in multiplier 4 Example: 001110011 4 Working from Right to Left, any “run of 1’s” is equal to: - value of first digit that’s one +value of first digit that’s zero 4 Example : 001110011 • First run: -1 + 4 = 3 • Second run: -16 + 128 = 112 • Total: 112 + 3 = 115 Lecture 8 - Mult. & Division 43

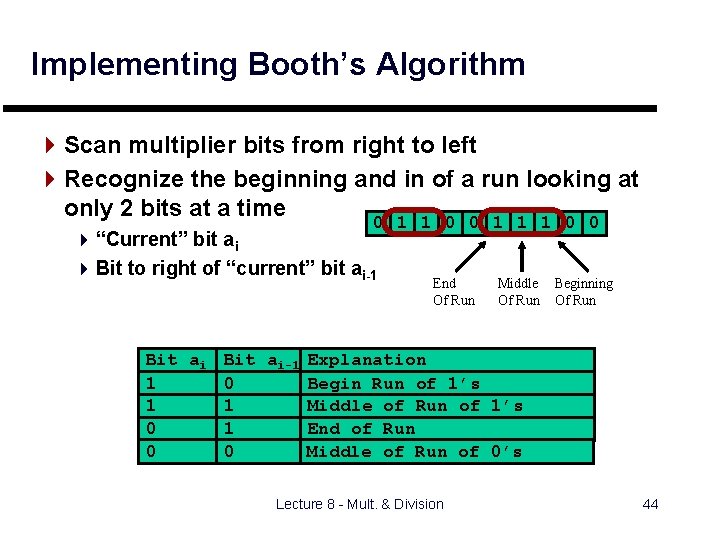
Implementing Booth’s Algorithm 4 Scan multiplier bits from right to left 4 Recognize the beginning and in of a run looking at only 2 bits at a time 0 1 1 0 0 1 1 1 0 0 4 “Current” bit ai 4 Bit to right of “current” bit ai-1 Bit ai 1 1 0 0 Bit ai-1 0 1 1 0 End Of Run Middle Of Run Beginning Of Run Explanation Begin Run of 1’s Middle of Run of 1’s End of Run Middle of Run of 0’s Lecture 8 - Mult. & Division 44

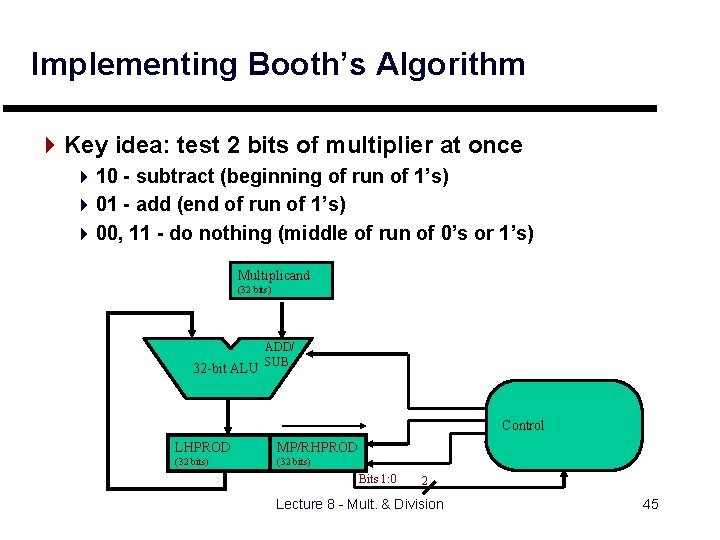
Implementing Booth’s Algorithm 4 Key idea: test 2 bits of multiplier at once 4 10 - subtract (beginning of run of 1’s) 4 01 - add (end of run of 1’s) 4 00, 11 - do nothing (middle of run of 0’s or 1’s) Multiplicand (32 bits) 32 -bit ALU ADD/ SUB Control Product LHPROD Shift Left MP/RHPROD (64 bits) (32 bits) Write Bits 1: 0 2 Lecture 8 - Mult. & Division 45

ECE 313 Fall 2006 Lecture 8 - Mult. & Division 46

Outline - Multiplication and Division 4 Multiplication 4 Review: Shift & Add Multiplication 4 Review: Booth’s Algorithm 4 MIPS Multiplication Instructions 3 4 Division 4 Summary Lecture 8 - Mult. & Division 47

Multiply Instructions in MIPS 4 MIPS adds new registers for product result: 4 Hi - upper 32 bits of product 4 Lo - lower 32 bits of product 4 MIPS multiply instructions 4 mult $s 0, $s 1 4 multu $s 0, $s 1 4 Accessing Hi, Lo registers 4 mfhi $s 1 4 mflo $s 1 Lecture 8 - Mult. & Division 48

Outline - Multiplication and Division 4 Multiplication 4 Review: Shift & Add Multiplication 4 Review: Booth’s Algorithm 4 Combinational Multiplication 4 MIPS Multiplication Instructions 4 Division Algorithms 3 4 MIPS Division Instructions 4 Summary Lecture 8 - Mult. & Division 49

Division Overview 4 Grammar school algorithm: long division 4 Subtract shifted divisor from dividend when it “fits” 4 Quotient bit: 1 or 0 4 Question: how can hardware tell “when it fits? ” 1001 Quotient Divisor 1000 1001010 -1000 10 Dividend Remainder Dividend = Quotient X Divisor + Remainder Lecture 8 - Mult. & Division 50

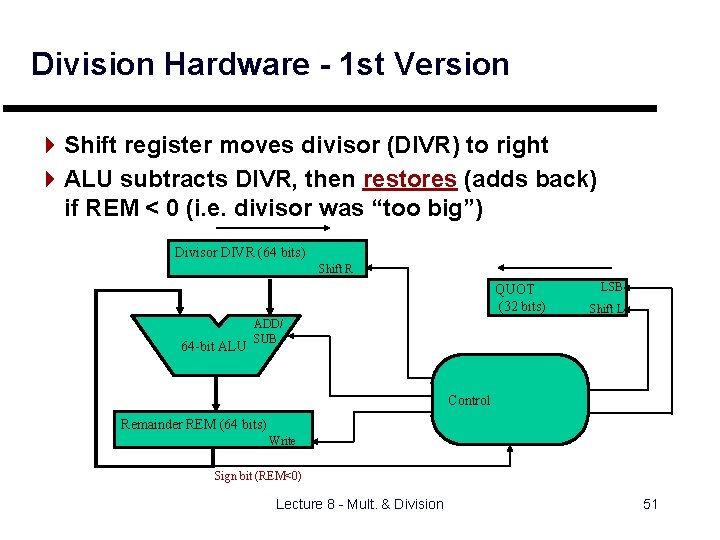
Division Hardware - 1 st Version 4 Shift register moves divisor (DIVR) to right 4 ALU subtracts DIVR, then restores (adds back) if REM < 0 (i. e. divisor was “too big”) Divisor DIVR (64 bits) Shift R QUOT (32 bits) 64 -bit ALU LSB Shift L ADD/ SUB Control Remainder REM (64 bits) Write Sign bit (REM<0) Lecture 8 - Mult. & Division 51

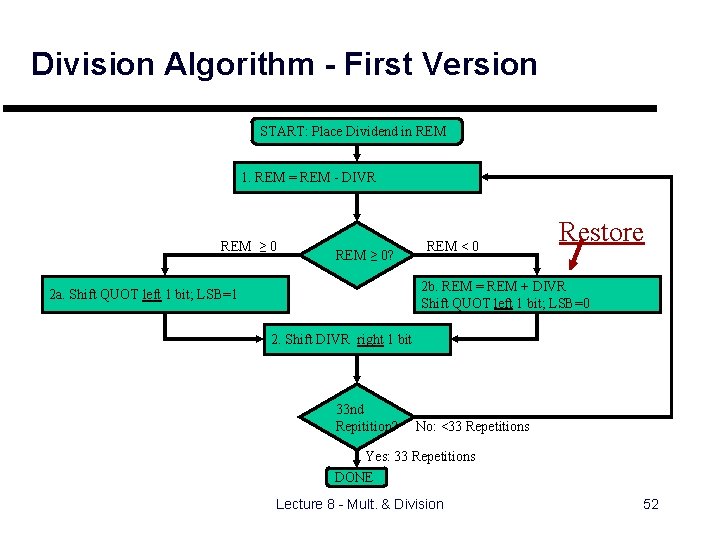
Division Algorithm - First Version START: Place Dividend in REM 1. REM = REM - DIVR REM ≥ 0? REM < 0 Restore 2 b. REM = REM + DIVR Shift QUOT left 1 bit; LSB=0 2 a. Shift QUOT left 1 bit; LSB=1 2. Shift DIVR right 1 bit 33 nd Repitition? No: <33 Repetitions Yes: 33 Repetitions DONE Lecture 8 - Mult. & Division 52

Divide 1 st Version - Observations 4 We only subtract 32 bits in each iteration 4 Idea: Instead of shifting divisor to right, shift remainder to left 4 First step cannot produce a 1 in quotient bit 4 Switch order to shift first, then subtract 4 Save 1 iteration Lecture 8 - Mult. & Division 53

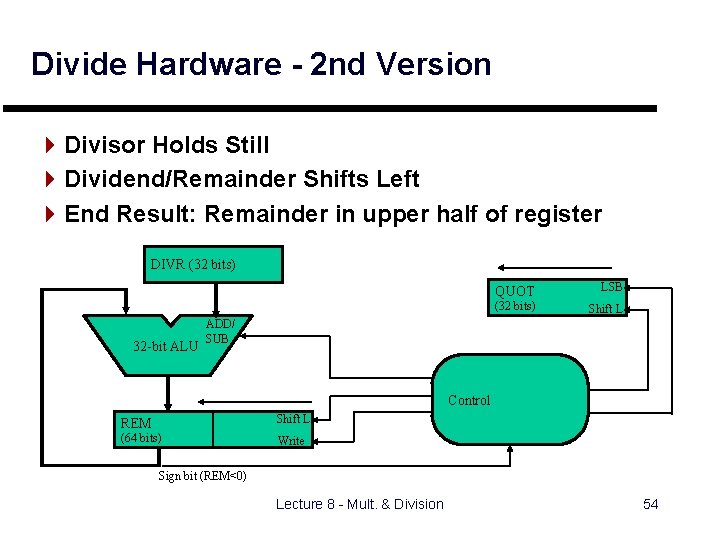
Divide Hardware - 2 nd Version 4 Divisor Holds Still 4 Dividend/Remainder Shifts Left 4 End Result: Remainder in upper half of register DIVR (32 bits) 32 -bit ALU QUOT LSB (32 bits) Shift L ADD/ SUB Control REM Shift L (64 bits) Write Sign bit (REM<0) Lecture 8 - Mult. & Division 54

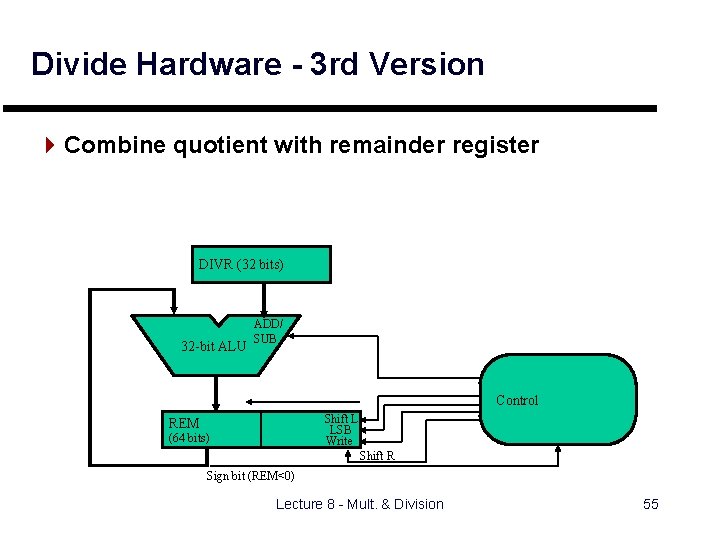
Divide Hardware - 3 rd Version 4 Combine quotient with remainder register DIVR (32 bits) 32 -bit ALU ADD/ SUB Control Shift L LSB Write REM (64 bits) Shift R Sign bit (REM<0) Lecture 8 - Mult. & Division 55

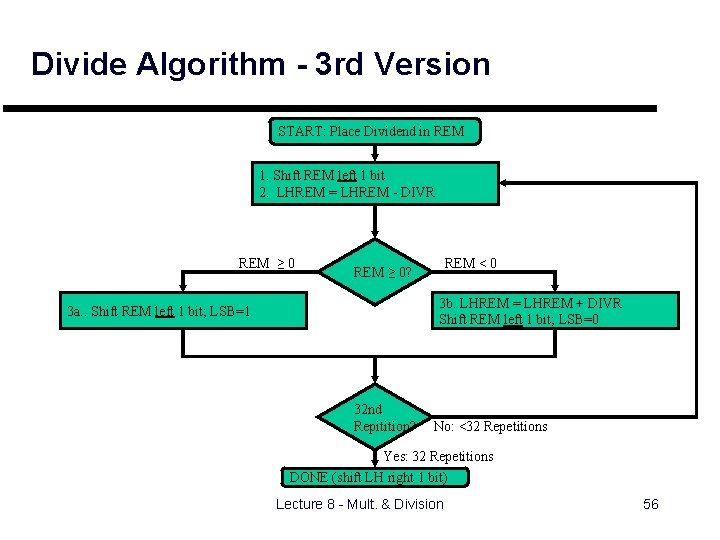
Divide Algorithm - 3 rd Version START: Place Dividend in REM 1. Shift REM left 1 bit 2. LHREM = LHREM - DIVR REM ≥ 0 REM < 0 REM ≥ 0? 3 b. LHREM = LHREM + DIVR Shift REM left 1 bit; LSB=0 3 a. . Shift REM left 1 bit; LSB=1 32 nd Repitition? No: <32 Repetitions Yes: 32 Repetitions DONE (shift LH right 1 bit) Lecture 8 - Mult. & Division 56

Dividing Signed Numbers 4 Check sign of divisor, dividend 4 Negate quotient if signs of operands are opposite 4 Make remainder sign match dividend (if nonzero) Lecture 8 - Mult. & Division 57

Outline - Multiplication and Division 4 Multiplication 4 Review: Shift & Add Multiplication 4 Review: Booth’s Algorithm 4 Combinational Multiplication 4 MIPS Multiplication Instructions 4 Division Algorithms 4 MIPS Division Instructions 3 4 Summary Lecture 8 - Mult. & Division 58

MIPS Divide Instructions 4 Results in Lo, Hi registers 4 Hi: remainder 4 Lo: quotient 4 Divide pseudoinstructions 4 div $s 3, $s 2, $s 1 4 divu $s 3, $s 2, $s 1 # $s 3 = $s 2 / $s 1 4 Software must check for overflow, divide-by-zero Lecture 8 - Mult. & Division 59

Outline - Multiplication and Division 4 Multiplication 4 Review: Shift & Add Multiplication 4 Review: Booth’s Algorithm 4 Combinational Multiplication 4 MIPS Multiplication Instructions 4 Division Algorithms 4 MIPS Division Instructions 4 Summary 3 Lecture 8 - Mult. & Division 60