CSE 575 Computer Arithmetic Spring 2003 Mary Jane

CSE 575 Computer Arithmetic Spring 2003 Mary Jane Irwin (www. cse. psu. edu/~mji) Computer Arithmetic CSE 575 Residue Arithmetic. 1 © MJIrwin, PSU, 2003

Residue Number System l l l Positional - value of symbol is position dependent Mixed radix - the number is represented by the residues wrt k pairwise relatively prime moduli (bases) mk-1 > … m 1 > m 0 (e. g. , 8 > 7 > 5 > 3) Digit set - for the ith position is [0, mi -1] xi = X mod mi = (X)mi l Range - number of distinct values is the product M of the k pairwise moduli RNS(8|7|5|3) gives 840 distinct values Computer Arithmetic CSE 575 Residue Arithmetic. 2 © MJIrwin, PSU, 2003

RNS Machine Representation l In practice, each residue is encoded in binary = 11 bits mod 8 l mod 7 mod 5 mod 3 So the representational efficiency is much less than with binary 840/2048 = 41% Computer Arithmetic CSE 575 Residue Arithmetic. 3 © MJIrwin, PSU, 2003

RNS(8|7|5|3) Examples (0|0|0|0)RNS(8|7|5|3) (1|1|1|1)RNS(8|7|5|3) (2|2|2|2)RNS(8|7|5|3) (0|1|3|2)RNS(8|7|5|3) (5|0|1|0)RNS(8|7|5|3) (0|1|4|1)RNS(8|7|5|3) represents 0 or 840 or … represents 1 or 841 or … represents 2 or 842 or … represents 8 or 848 or … represents 21 or 861 or … represents 64 or 904 or … (2|0|0|2)RNS(8|7|5|3) represents -70 or 770 or … (7|6|4|2)RNS(8|7|5|3) represents -1 or 839 or … Computer Arithmetic CSE 575 Residue Arithmetic. 4 © MJIrwin, PSU, 2003

Representing Negative Numbers l l l Since (-X)mi = (M - X)mi can shift the range from 0 to M to –M/2 to M/2 – 1 or any other interval of M consecutive integers Negative numbers are represented using a complement system with the complementation constant M Given the RNS of X, the representation of –X can be found by complementing each of the digits xi wrt its moduli mi (0 digits unchanged) Computer Arithmetic CSE 575 Residue Arithmetic. 5 © MJIrwin, PSU, 2003

RNS(5|3|2) Complement Coding M = 5 x 3 x 2 = 30 distinct values that can be mapped to 0 to 29 or – 15 to +14 421 000 111 220 310 -1 0 +1 -2 +2 201 301 -3 +3 increment 120 -4 +4 410 … +5 021 … -13 221 -14 -15+14 420 110 +13 = 3 | 1 001 -13 = Computer Arithmetic CSE 575 Residue Arithmetic. 7 5 -3 | 3 -1 | 2 -1 = 2 | 1 © MJIrwin, PSU, 2003

Residue Arithmetic l Negation » Independently complementing each of the moduli digits (e. g. , mi – xi) 1 = (1|1|1|1)RNS(8|7|5|3) then -1 = (8 -1|7 -1|5 -1|3 -1)RNS(8|7|5|3) = (7|6|4|2)RNS(8|7|5|3) l Similarly, addition, subtraction, and multiplication are performed by independently operating on each moduli digit » Since each digit is a relatively small number, digit operations are quite fast and simple in RNS Computer Arithmetic CSE 575 Residue Arithmetic. 8 © MJIrwin, PSU, 2003

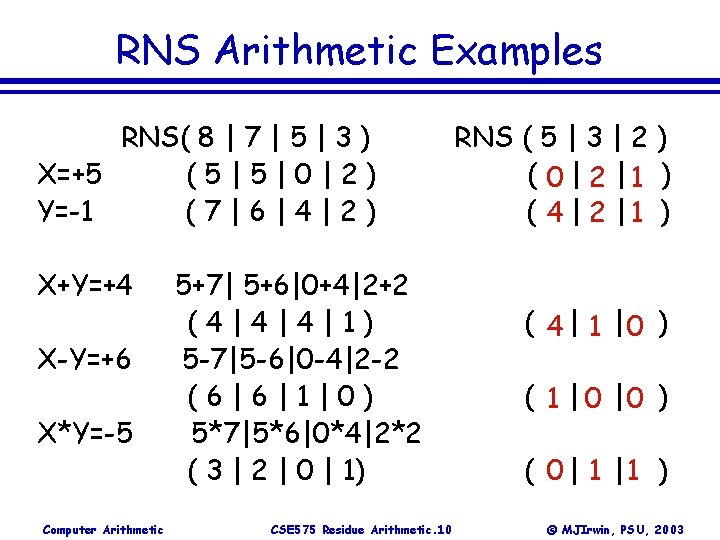
RNS Arithmetic Examples RNS( 8 | 7 | 5 | 3 ) X=+5 (5|5|0|2) Y=-1 (7|6|4|2) X+Y=+4 X-Y=+6 X*Y=-5 Computer Arithmetic 5+7| 5+6|0+4|2+2 (4|4|4|1) 5 -7|5 -6|0 -4|2 -2 (6|6|1|0) 5*7|5*6|0*4|2*2 ( 3 | 2 | 0 | 1) CSE 575 Residue Arithmetic. 10 RNS ( 5 | 3 | 2 ) ( 0 | 2 |1 ) ( 4 | 1 |0 ) ( 1 | 0 |0 ) ( 0 | 1 |1 ) © MJIrwin, PSU, 2003

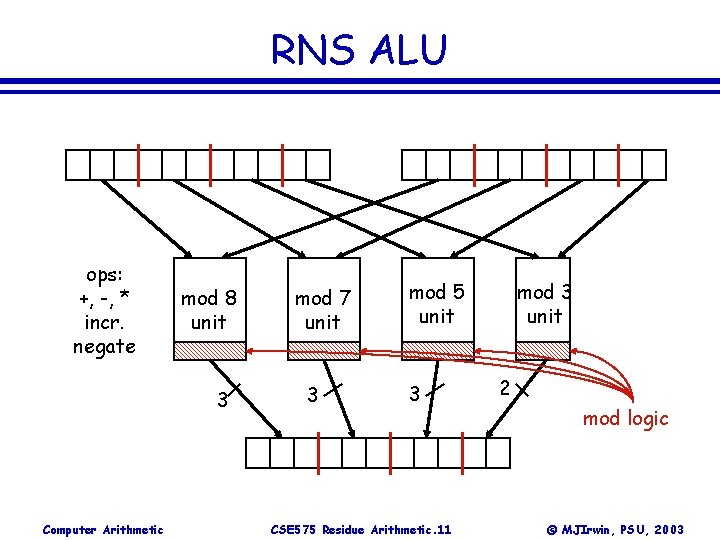
RNS ALU ops: +, -, * incr. negate mod 8 unit 3 Computer Arithmetic mod 7 unit 3 mod 5 unit 3 CSE 575 Residue Arithmetic. 11 mod 3 unit 2 mod logic © MJIrwin, PSU, 2003

Residue Arithmetic, Con’t l Unfortunately, the complexity of division and auxiliary operations like sign test, magnitude comparison, and overflow detection can nullify gains (7|2|2|1)RNS(8|7|5|3) (2|5|0|1)RNS(8|7|5|3) » which are negative? , which is larger? , does (1|0|2|2)RNS(8|7|5|3) represent their true sum as opposed to the residue of their sum modulo 840 (i. e. , overflow)? Computer Arithmetic CSE 575 Residue Arithmetic. 12 © MJIrwin, PSU, 2003

Selecting the Moduli l All moduli must be relatively prime » powers of any two prime numbers are relatively prime l Product of the moduli determines the range of the system » so bigger moduli increase the range l Largest module dictates the speed of arithmetic operations (worst case carry) » try for moduli close to together so that all moduli positions take about the same time to do an arithmetic operation Computer Arithmetic CSE 575 Residue Arithmetic. 13 © MJIrwin, PSU, 2003

Selecting the Moduli, Con’t l Moduli with powers-of-2 (mi = 2 k) give the most efficient encoding into binary » k bits can encode exactly 2 k distinct values l Arithmetic units with mi = 2 k or mi = 2 k - 1 are easiest to design » can use simple 2 s’c and 1 s’c binary adders/subtractors/ multipliers » don’t have to do the trailing mod operations (hardware does it automatically !) Computer Arithmetic CSE 575 Residue Arithmetic. 14 © MJIrwin, PSU, 2003

Picking Good Moduli l Any list of relatively prime numbers ak-2 > … a 1 > a 0 can be the basis of the k modulus RNS(2 ak-2|2 ak-2 -1| …| 2 a 1 -1| 2 a 0 -1) l To maximize the dynamic range, the even modulus is chosen to be as large as possible Computer Arithmetic CSE 575 Residue Arithmetic. 15 © MJIrwin, PSU, 2003

Some Good Moduli Choices RNS(23| 23 -1| 22 -1) (8|7|3) M = 168; 8 b RNS(24| 24 -1| 23 -1) (16|15|7) M = 1680; 11 b RNS(25| 25 -1| 23 -1|22 -1|) (32|31|7|3) M = 20, 832; 15 b RNS(25| 25 -1| 24 -1|23 -1|) (32|31|15|7) M = 104, 160; 17 b RNS(26| 26 -1| 25 -1) (64|63|31) M = 124, 992; 17 b RNS(27| 27 -1| 26 -1|25 -1|) (128|127|63|31) M = 31, 747, 968; 25 b Computer Arithmetic CSE 575 Residue Arithmetic. 16 © MJIrwin, PSU, 2003

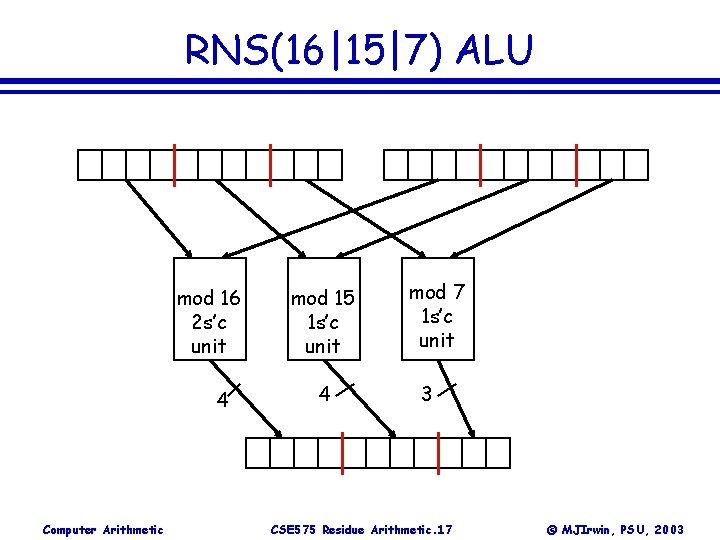
RNS(16|15|7) ALU mod 16 2 s’c unit 4 Computer Arithmetic mod 15 1 s’c unit 4 mod 7 1 s’c unit 3 CSE 575 Residue Arithmetic. 17 © MJIrwin, PSU, 2003

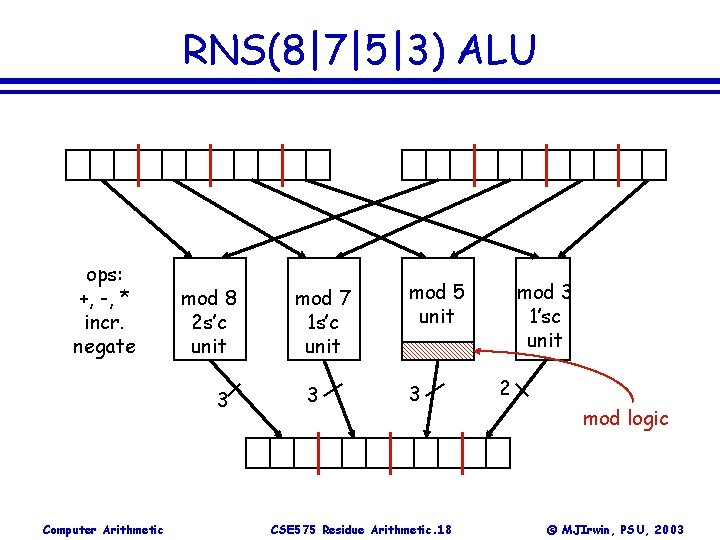
RNS(8|7|5|3) ALU ops: +, -, * incr. negate mod 8 2 s’c unit 3 Computer Arithmetic mod 7 1 s’c unit 3 mod 5 unit 3 CSE 575 Residue Arithmetic. 18 mod 3 1’sc unit 2 mod logic © MJIrwin, PSU, 2003

RNS Conversion l Conversion from binary/decimal to RNS » Given a number y, find its residues with respect to the moduli mi, 0 i k-1 » Can use some table lookup short cuts to avoid the divisions l Conversion from RNS to binary/decimal » Makes use of the Chinese remainder theorem Computer Arithmetic CSE 575 Residue Arithmetic. 19 © MJIrwin, PSU, 2003

RNS Suitable Applications ASIC parts that don’t have to conform to the floating point standard l 1, 000’s of operations after input conversion before output conversion is necessary l Never have to do sign detect, overflow detect, comparison, division l Some signal processing operations (e. g. , filters) l Computer Arithmetic CSE 575 Residue Arithmetic. 20 © MJIrwin, PSU, 2003

Key References Garner, The Residue Number System, IRE Trans. Electronic Computers, Vol. 8, pp. 140 -147, June 1959. Jenkins, Finite Arithmetic Concepts, in Handbook for Digital Signal Processing, pp. 611 -675, Wiley, 1993. Parhami, Computer Arithmetic, Oxford Univ. Press, 1999. Soderstrand, Jenkins, Jullien, Taylor, Residue Number System Arithmetic, IEEE Press, 1986. Szabo, Tanaka, Residue Arithmetic and Its Applications to Computer Technology, Mc. Graw-Hill, 1967. Computer Arithmetic CSE 575 Residue Arithmetic. 21 © MJIrwin, PSU, 2003