CSE 554 Lecture 7 Deformation II Fall 2011

CSE 554 Lecture 7: Deformation II Fall 2011 CSE 554 Deformation II Slide 1

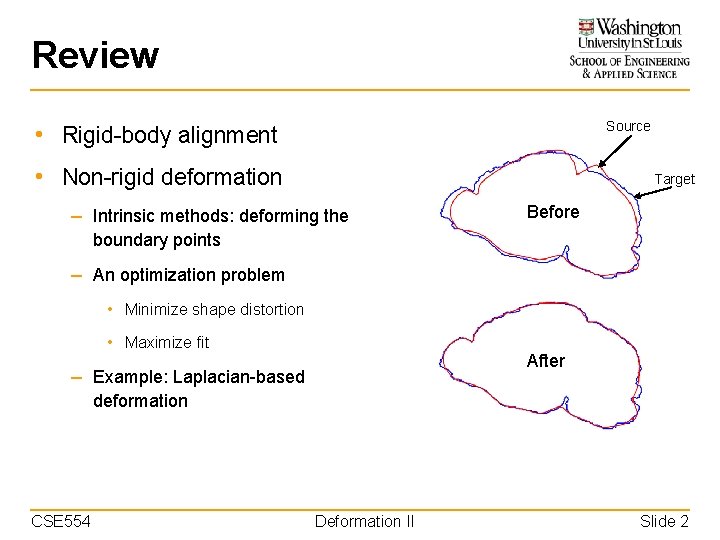
Review Source • Rigid-body alignment • Non-rigid deformation Target – Intrinsic methods: deforming the Before boundary points – An optimization problem • Minimize shape distortion • Maximize fit After – Example: Laplacian-based deformation CSE 554 Deformation II Slide 2

Extrinsic Deformation • Computing deformation of each point in the plane or volume – Not just points on the boundary curve or surface Credits: Adams and Nistri, BMC Evolutionary Biology (2010) CSE 554 Deformation II Slide 3

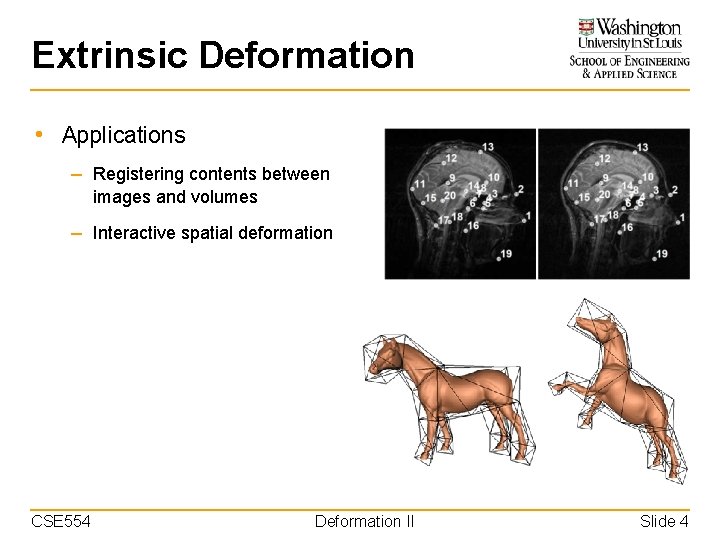
Extrinsic Deformation • Applications – Registering contents between images and volumes – Interactive spatial deformation CSE 554 Deformation II Slide 4

Techniques • Thin-plate spline deformation • Free form deformation • Cage-based deformation CSE 554 Deformation II Slide 5

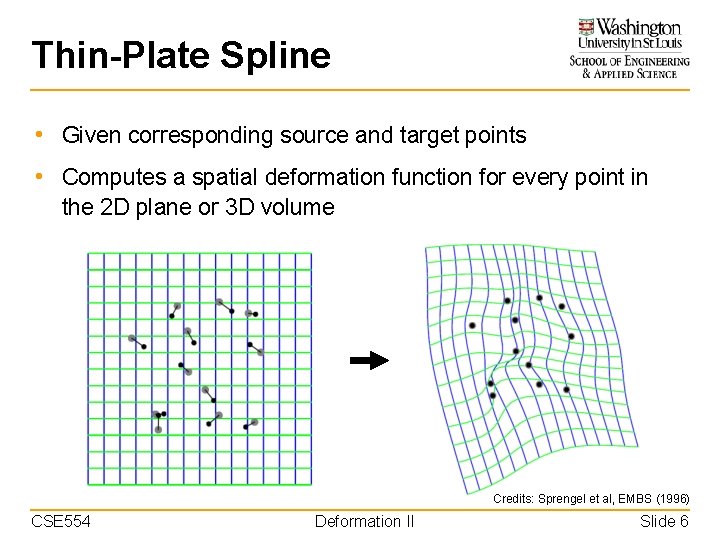
Thin-Plate Spline • Given corresponding source and target points • Computes a spatial deformation function for every point in the 2 D plane or 3 D volume Credits: Sprengel et al, EMBS (1996) CSE 554 Deformation II Slide 6

Thin-Plate Spline • A minimization problem – Minimizing distances between source and target points – Minimizing distortion of the space (as if bending a thin sheet of metal) • There is a closed-form solution – Solving a linear system of equations CSE 554 Deformation II Slide 7

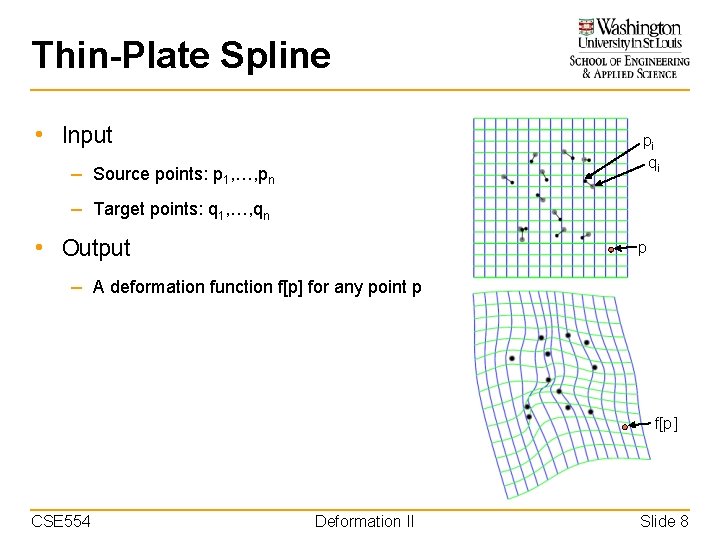
Thin-Plate Spline • Input pi qi – Source points: p 1, …, pn – Target points: q 1, …, qn • Output p – A deformation function f[p] for any point p f[p] CSE 554 Deformation II Slide 8

Thin-Plate Spline • Minimization formulation – Ef: fitting term • Measures how close is the deformed source to the target – Ed: distortion term • Measures how much the space is warped – : weight • Controls how much non-rigid warping is allowed CSE 554 Deformation II Slide 9

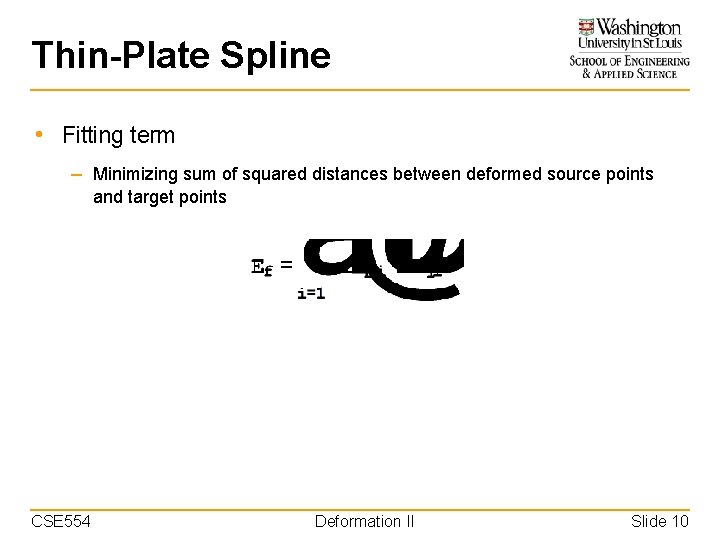
Thin-Plate Spline • Fitting term – Minimizing sum of squared distances between deformed source points and target points CSE 554 Deformation II Slide 10

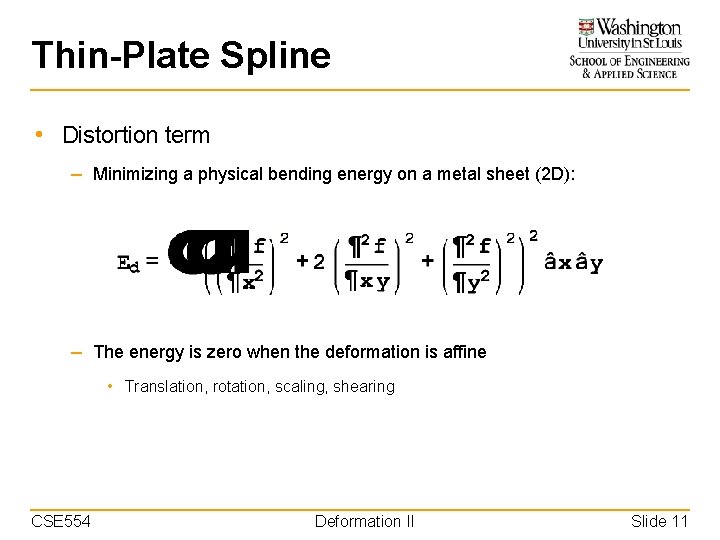
Thin-Plate Spline • Distortion term – Minimizing a physical bending energy on a metal sheet (2 D): – The energy is zero when the deformation is affine • Translation, rotation, scaling, shearing CSE 554 Deformation II Slide 11

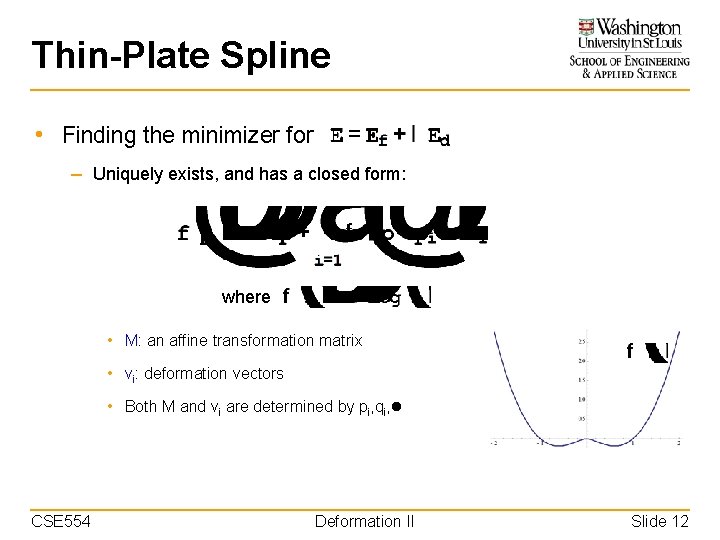
Thin-Plate Spline • Finding the minimizer for – Uniquely exists, and has a closed form: where • M: an affine transformation matrix • vi: deformation vectors • Both M and vi are determined by pi, qi, CSE 554 Deformation II Slide 12

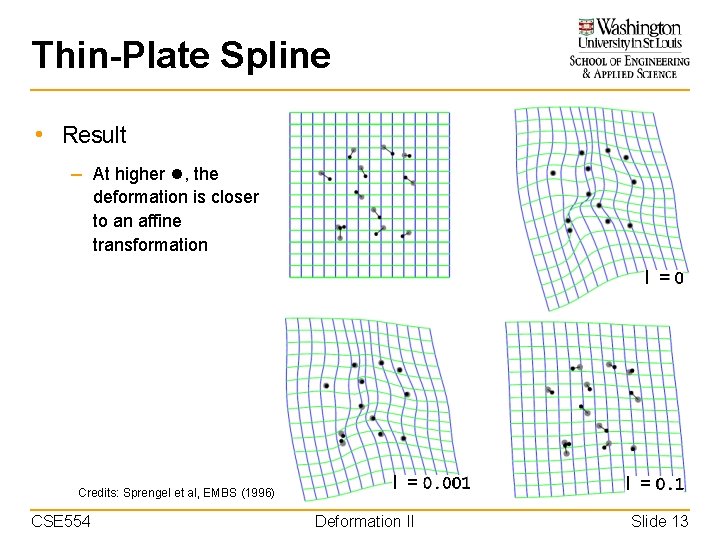
Thin-Plate Spline • Result – At higher , the deformation is closer to an affine transformation Credits: Sprengel et al, EMBS (1996) CSE 554 Deformation II Slide 13

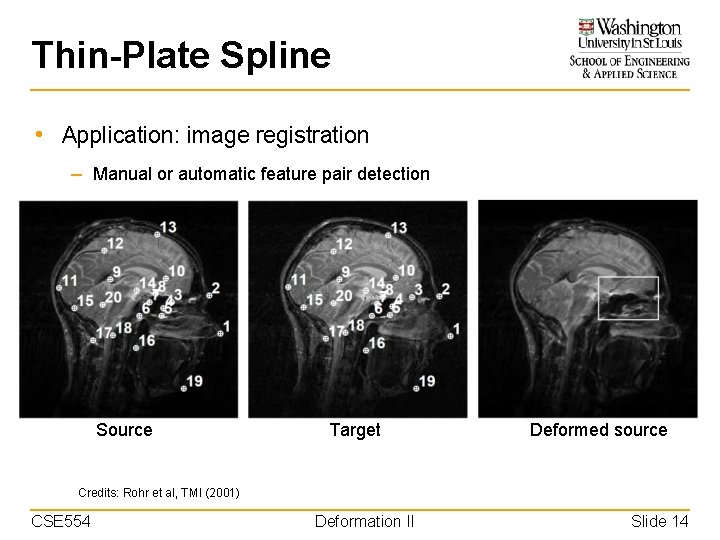
Thin-Plate Spline • Application: image registration – Manual or automatic feature pair detection Source Target Deformed source Credits: Rohr et al, TMI (2001) CSE 554 Deformation II Slide 14

Thin-Plate Spline • Advantages – Smooth deformations, with physical analogy – Closed-form solution – Few free parameters (no tuning is required) • Disadvantages – Solving the equations still takes time (hence cannot perform “Interactive” deformation) CSE 554 Deformation II Slide 15

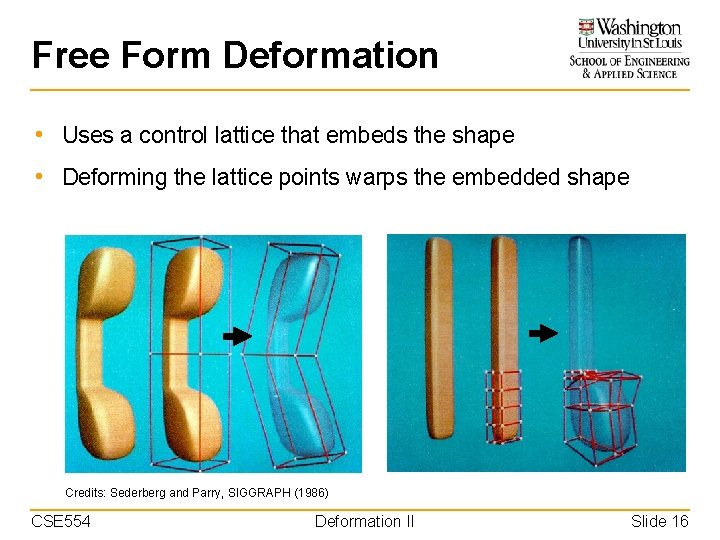
Free Form Deformation • Uses a control lattice that embeds the shape • Deforming the lattice points warps the embedded shape Credits: Sederberg and Parry, SIGGRAPH (1986) CSE 554 Deformation II Slide 16

Free Form Deformation • Warping the space by “blending” the deformation at the control points – Each deformed point is a weighted sum of deformed lattice points CSE 554 Deformation II Slide 17

Free Form Deformation • Input – Source lattice points: p 1, …, pn – Target lattice points: q 1, …, qn • Output – A deformation function f[p] for any p f[p] point p in the lattice grid: pi qi • wi[p]: determined by relative position of p with respect to pi CSE 554 Deformation II Slide 18

Free Form Deformation • Desirable properties of the weights wi[p] – Greater when p is closer to pi • So that the influence of each control point is local – Smoothly varies with location of p • So that the deformation is smooth p f[p] – • So that f[p] = wi[p] qi is an affine combination of qi pi qi – • So that f[p]=p if the lattice stays unchanged CSE 554 Deformation II Slide 19

Free Form Deformation • Finding weights (2 D) – Let the lattice points be pi, j for i=0, …, k and j=0, …, l – Compute p’s relative location in the grid (s, t) • Let (xmin, xmax), (ymin, ymax) be the range of grid p 0, 2 t p 1, 2 p 2, 2 p 3, 2 p p 0, 1 p 1, 1 p 2, 1 p 3, 1 p 0, 0 p 1, 0 p 2, 0 p 3, 0 s CSE 554 Deformation II Slide 20

Free Form Deformation • Finding weights (2 D) – Let the lattice points be pi, j for i=0, …, k and j=0, …, l – Compute p’s relative location in the grid (s, t) – The weight wi, j for lattice point pi, j is: p 0, 2 t p 1, 2 p 2, 2 p 3, 2 p p 0, 1 p 1, 1 p 2, 1 p 3, 1 p 0, 0 p 1, 0 p 2, 0 p 3, 0 s • i, j: importance of pi, j • B: Bernstein basis function: CSE 554 Deformation II Slide 21

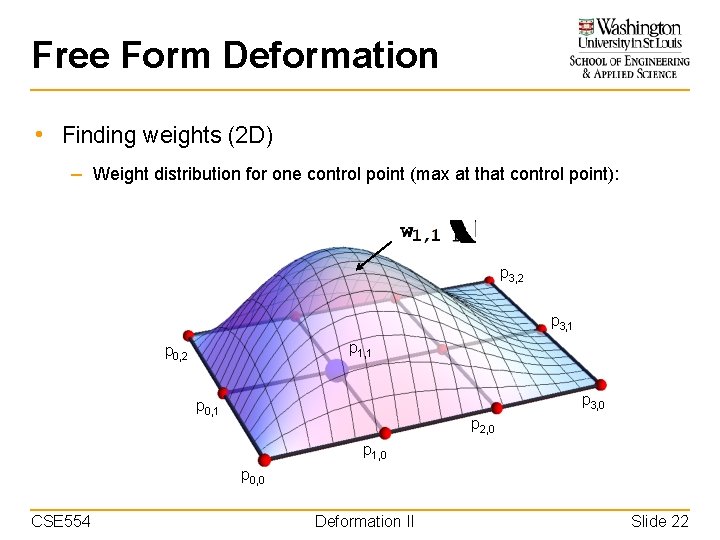
Free Form Deformation • Finding weights (2 D) – Weight distribution for one control point (max at that control point): p 3, 2 p 3, 1 p 1, 1 p 0, 2 p 3, 0 p 0, 1 p 2, 0 p 1, 0 p 0, 0 CSE 554 Deformation II Slide 22

Free Form Deformation • A deformation example CSE 554 Deformation II Slide 23

Free Form Deformation • Registration – Embed the source in a lattice – Compute new lattice positions over the target – Fitting term • Distance between deformed source shape and the target shape • Agreement of the deformed image content and the target image – Distortion term • Thin-plate spline energy • Non-folding constraint • Local rigidity constraint (to prevent stretching) CSE 554 Deformation II Slide 24

Free Form Deformation • Registration example Deformed w/o rigidity Source Deformed with rigidity Target Credits: Loeckx et al, MICCAI (2004) CSE 554 Deformation II Slide 25

Free Form Deformation • Advantages – Smooth deformations – Easy to implement (no equation solving) – Efficient and localized controls for interactive editing – Can be coupled with different fitting or energy objectives • Disadvantages – Too many lattice points in 3 D – The lattice structure is not suitable for organic, non-cubical shapes CSE 554 Deformation II Slide 26

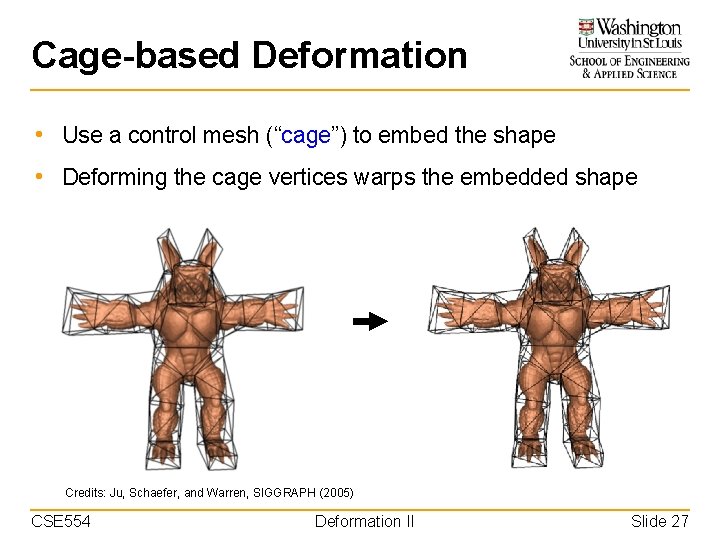
Cage-based Deformation • Use a control mesh (“cage”) to embed the shape • Deforming the cage vertices warps the embedded shape Credits: Ju, Schaefer, and Warren, SIGGRAPH (2005) CSE 554 Deformation II Slide 27

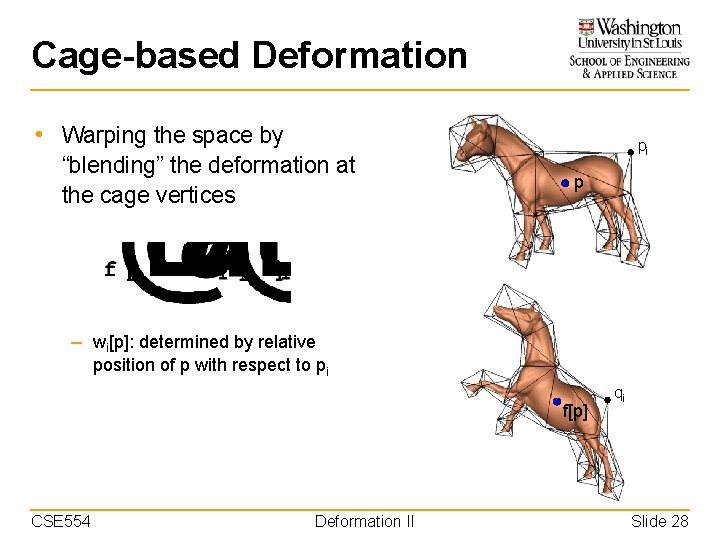
Cage-based Deformation • Warping the space by “blending” the deformation at the cage vertices pi p – wi[p]: determined by relative position of p with respect to pi f[p] CSE 554 Deformation II qi Slide 28

Cage-based Deformation • Finding weights (2 D) – Problem: given a closed polygon (cage) with vertices pi and an interior point p, find weights wi[p] such that: • 1) pi • 2) p • 3) They vary smoothly with p CSE 554 Deformation II Slide 29

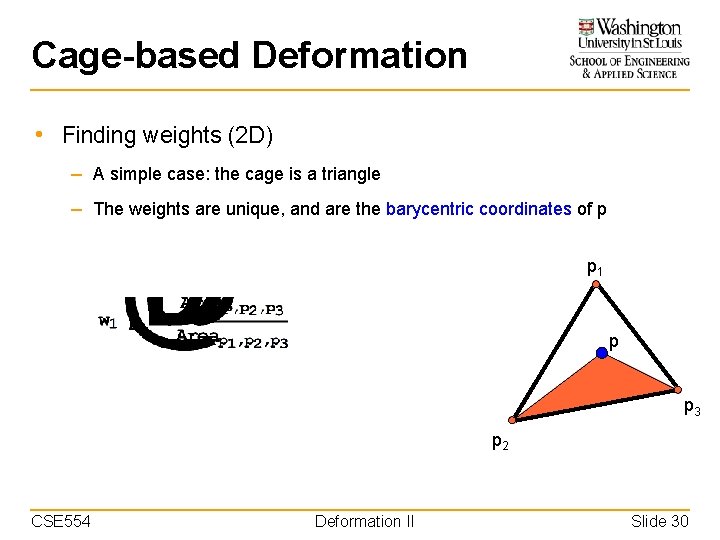
Cage-based Deformation • Finding weights (2 D) – A simple case: the cage is a triangle – The weights are unique, and are the barycentric coordinates of p p 1 p p 3 p 2 CSE 554 Deformation II Slide 30

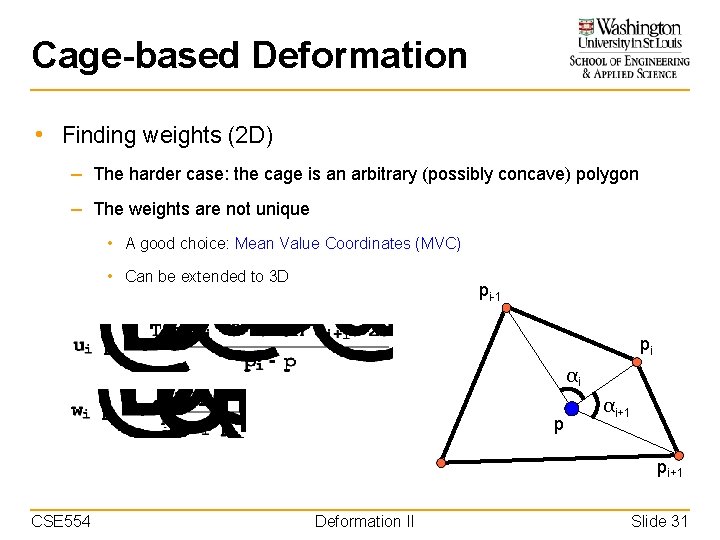
Cage-based Deformation • Finding weights (2 D) – The harder case: the cage is an arbitrary (possibly concave) polygon – The weights are not unique • A good choice: Mean Value Coordinates (MVC) • Can be extended to 3 D pi-1 pi αi p αi+1 pi+1 CSE 554 Deformation II Slide 31

Cage-based Deformation • Finding weights (2 D) – Weight distribution of one cage vertex in MVC: pi CSE 554 Deformation II Slide 32

Cage-based Deformation • Application: character animation – Using improved weights: Harmonic Coordinates CSE 554 Deformation II Slide 33

Cage-based Deformation • Registration – Embed source in a cage – Compute new locations of cage vertices over the target • Minimizing some fitting and energy objectives • Not seen in literature yet… future work! CSE 554 Deformation II Slide 34

Cage-based Deformation • Advantages over free form deformations – Much smaller number of control points – Flexible structure suitable for organic shapes • Disadvantages – Setting up the cage can be time-consuming – The cage needs to be a closed shape • Not as flexible as point handles CSE 554 Deformation II Slide 35

Further Readings • Thin-plate spline deformation – “Principal warps: thin-plate splines and the decomposition of deformations”, by Bookstein (1989) – “Landmark-Based Elastic Registration Using Approximating Thin-Plate Splines”, by Rohr et al. (2001) • Free form deformation – “Free-Form Deformation of Solid Geometric Models”, by Sederberg and Parry (1986) – “Extended Free-Form Deformation: A sculpturing Tool for 3 D Geometric Modeling”, by Coquillart (1990) • Cage-based deformation – “Mean value coordinates for closed triangular meshes”, by Ju et al. (2005) – “Harmonic coordinates for character animation”, by Joshi et al. (2007) – “Green coordinates”, by Lipman et al. (2008) CSE 554 Deformation II Slide 36