CSE 522 Modelbased Development 1 Computer Science Engineering

CSE 522 Model-based Development (1) Computer Science & Engineering Department Arizona State University Tempe, AZ 85287 Dr. Yann-Hang Lee yhlee@asu. edu (480) 727 -7507 Some of the slides were based on lectures by Lee & Seshia (UC Berkeley) and Fainekos (ASU)

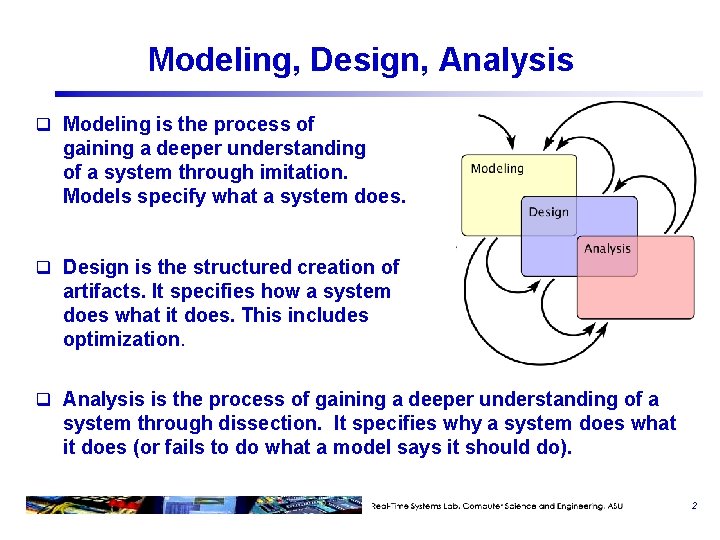
Modeling, Design, Analysis q Modeling is the process of gaining a deeper understanding of a system through imitation. Models specify what a system does. q Design is the structured creation of artifacts. It specifies how a system does what it does. This includes optimization. q Analysis is the process of gaining a deeper understanding of a system through dissection. It specifies why a system does what it does (or fails to do what a model says it should do). 2

What is Modeling? q A mathematical model in the form of a set of definitions and mathematical formulas. v Use mathematical objects to describe the (dynamical or static) properties and behavior of the system v Developing insight about a system, process, or artifact through imitation. v The artifact that imitates the system, process, or artifact of interest. q Mathematical models can help us v understand the system behavior v predict the system behavior v analyze the system behavior v identify system parameters 3

What is Model-Based Design? q Create a mathematical model of all the parts of the embedded system v Physical world v Control system v Software environment v Hardware platform v Network v Sensors and actuators q Construct the implementation from the model v Construction may be automated, like a compiler v More commonly, portions are automatically constructed 4

When is a Design of a System “Correct”? q A design is correct when it meets its specification (requirements) in its operating environment q “A design without specification cannot be right or wrong, it can only be surprising!” q Simply running a few tests is not enough! q Many embedded systems are deployed in safety-critical applications (avionics, automotive, medical, …)

Specification, Verification, and Control Specification A mathematical statement of the design objective (desired properties of the system) Verification Synthesis Does the designed system achieve its objective in the operating environment? Given an incomplete design, synthesize a strategy to complete the system so that it achieves its objective in the operating environment

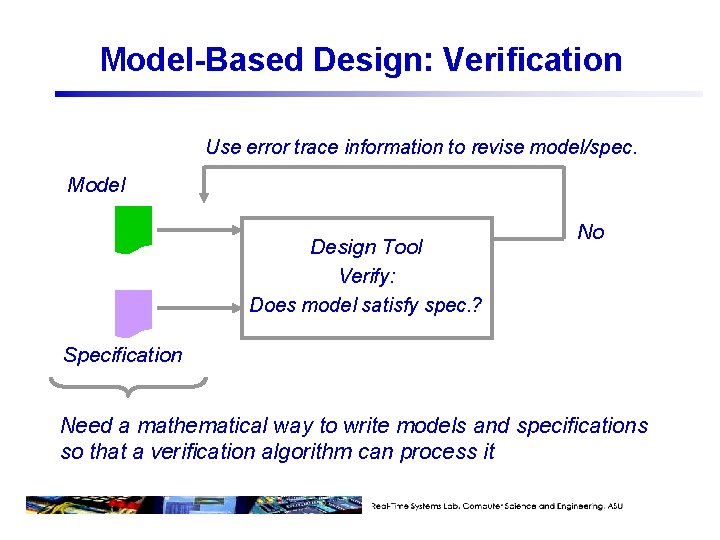
Model-Based Design: Verification Use error trace information to revise model/spec. Model Design Tool Verify: Does model satisfy spec. ? No Specification Need a mathematical way to write models and specifications so that a verification algorithm can process it

Model-Based Design: Synthesis Partial Description of the Model Automatic Model Synthesis Tool Specification Automatic code synthesis for specific platform Need a mathematical way to write models and specifications so that an algorithm can process it

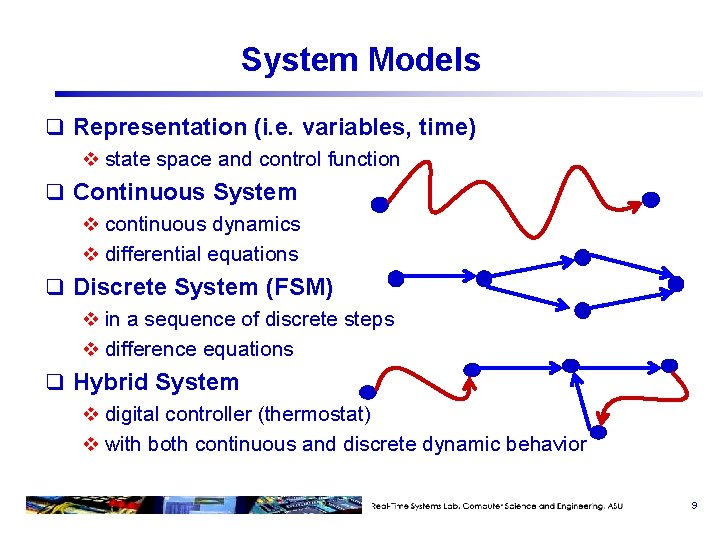
System Models q Representation (i. e. variables, time) v state space and control function q Continuous System v continuous dynamics v differential equations q Discrete System (FSM) v in a sequence of discrete steps v difference equations q Hybrid System v digital controller (thermostat) v with both continuous and discrete dynamic behavior 9

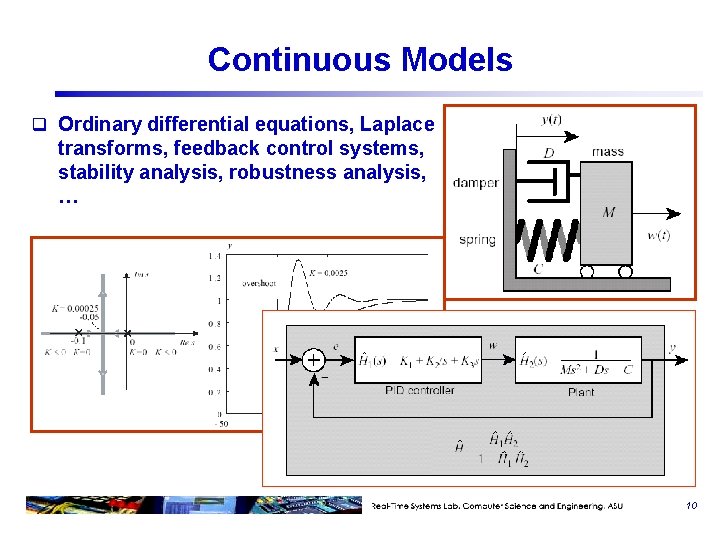
Continuous Models q Ordinary differential equations, Laplace transforms, feedback control systems, stability analysis, robustness analysis, … 10

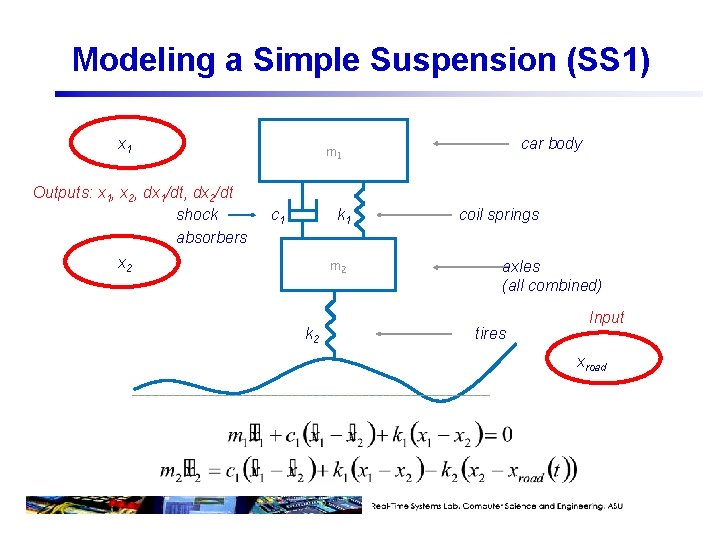
Modeling a Simple Suspension (SS 1) x 1 Outputs: x 1, x 2, dx 1/dt, dx 2/dt shock absorbers car body m 1 c 1 k 1 x 2 m 2 k 2 coil springs axles (all combined) tires Input xroad

Modeling a Simple Suspension (SS 1) q Recall: let us set and q Then where

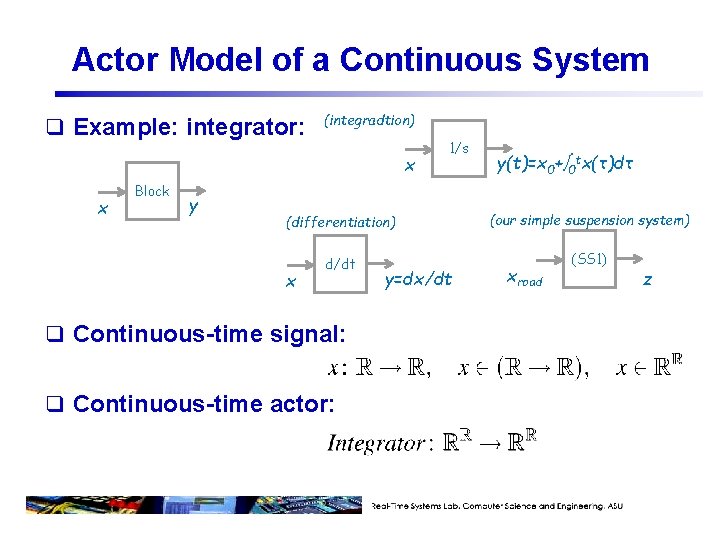
Actor Model of a Continuous System q Example: integrator: (integradtion) x x Block y 1/s y(t)=x 0+ 0 tx(τ)dτ (differentiation) (our simple suspension system) d/dt (SS 1) x q Continuous-time signal: q Continuous-time actor: y=dx/dt xroad z

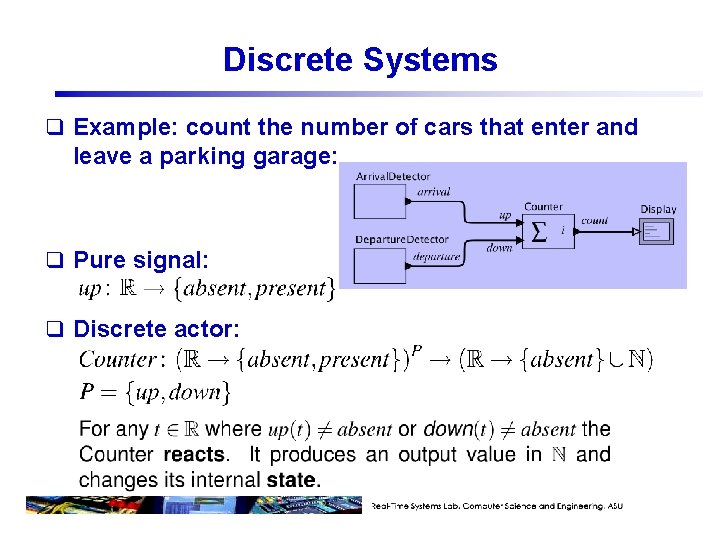
Discrete Systems q Example: count the number of cars that enter and leave a parking garage: q Pure signal: q Discrete actor:

Discrete Time Signals Consider a signal x : R + {absent} x R, where R is some range and let T be the points in time that it is present T = {t R + | x(t) absent}. Then, x is discrete if there exists 1 -1 function f : T N which is order preserving. The system is event triggered. present absent up : N + {absent, present} t

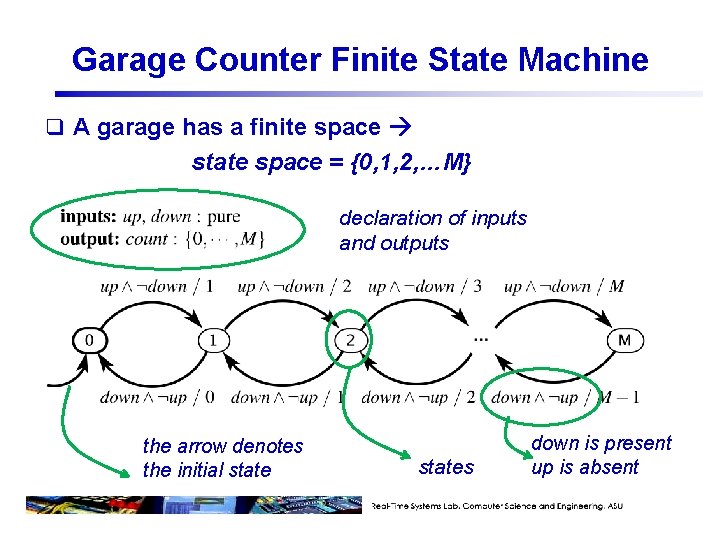
Garage Counter Finite State Machine q A garage has a finite space state space = {0, 1, 2, …M} declaration of inputs and outputs the arrow denotes the initial states down is present up is absent

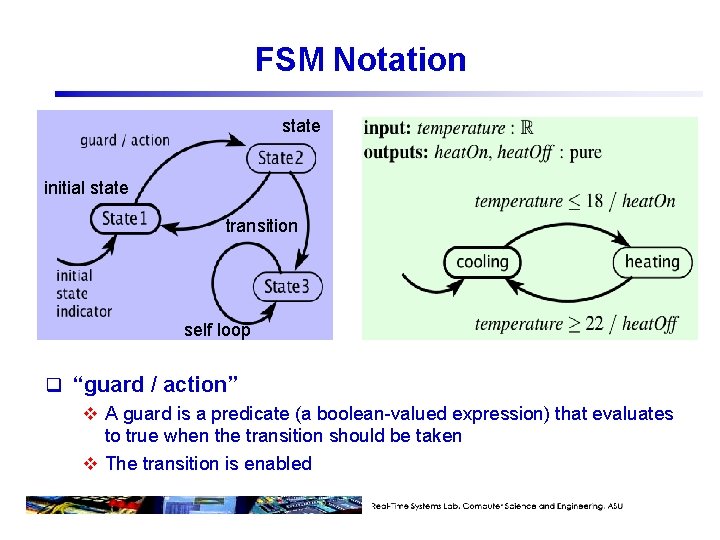
FSM Notation state initial state transition self loop q “guard / action” v A guard is a predicate (a boolean-valued expression) that evaluates to true when the transition should be taken v The transition is enabled

Formal Definition of FSM q An FSM (finite state automaton) is a 5 -tuple (states, inputs, outputs, update, initialstate) where v States is a finite set of states v Inputs is a set of input valuations v Outputs is a set of output valuations v update : States x Inputs States x Outputs is an update function, mapping a state and input valuation to a next state and an output valuation v initial. State is the initial state

Garage Counter Mathematical Model The picture above defines the update function.

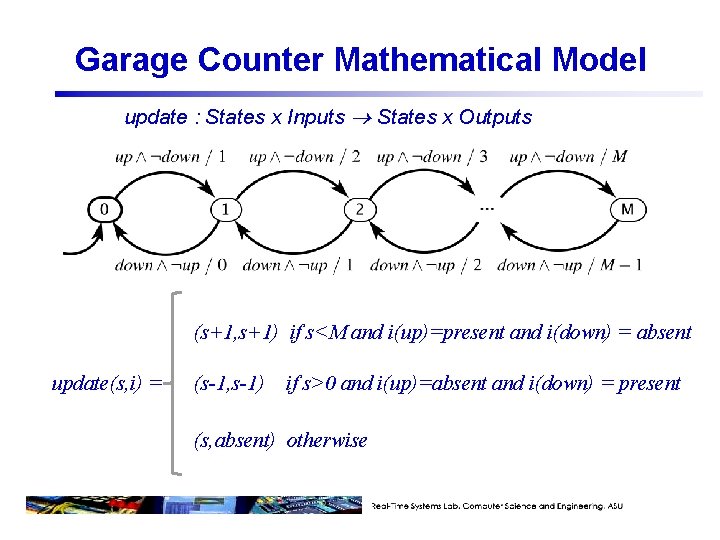
Garage Counter Mathematical Model update : States x Inputs States x Outputs (s+1, s+1) if s<M and i(up)=present and i(down) = absent update(s, i) = (s-1, s-1) if s>0 and i(up)=absent and i(down) = present (s, absent) otherwise

FSM Execution q The dynamics of a discrete system can be described by a sequence of reactions v We ignore how much time has passed between each reaction q For each reaction the FSM moves from the current state to the next state v s : N S is the state of FSM for each reaction q We can number the visited states (0 for the initial) q Input & output valuations x : N Inputs and y : N Ouputs q The FSM dynamics are (s(n+1), y(n)) = update(s(n), x(n))

FSM Behavior q Each port p, for each reaction will take a value from Vp {absent}, generating a sequence (or function) sp : N Vp {absent} q Behavior: the assignment of signals to each input port such that an output sequence can be produced v v Observable trace ((xi, yi))i N Execution trace ((xi, si, yi))i N q The set of all behaviors of an FSM M is called the language of M and it is denoted by L(M) 22

Garage Counter: Behavior: sup = (present, absent, present, …) sdown = (present, absent, …) scount = (absent, 1, 0, 1, …) Note if scount was something else, then this might not have been a behavior of the system.

Extended State Machines q A default transition is enabled if no non-default transition is enabled and it either has no guard or the guard is true. q Extended state machines augment the FSM model with variables that may be read or written. Question: What is the size of the state space?

Definitions q Stuttering transition: Implicit default transition that is enabled when inputs are absent and that produces absent outputs. q Receptiveness: For any input values, some transition is enabled. Our structure together with the implicit default transition ensures that our FSMs are receptive. q Determinism: In every state, for all input values, exactly one (possibly implicit) transition is enabled, i. e. next possible state is uniquely determined. q Non-deterministic: If for any state of a state machine, there are two distinct transitions with guards that can evaluate to true in the same reaction.

Example: Nondeterministic FSM q Nondeterministic model of pedestrians arriving at a crosswalk: q Formally, the update function is replaced by a function

Behaviors and Traces q FSM behavior is a sequence of (non-stuttering) steps. q A trace is the record of inputs, states, and outputs in a behavior. q A computation tree is a graphical representation of all possible traces. q FSMs are suitable formal analysis. For example, safety analysis might show that some unsafe state is not reachable.

Uses of Nondeterminism q Modeling unknown aspects of the environment or system v Such as: how the environment changes the i. Robot’s orientation q Hiding detail in a specification of the system v We will see an example of this later q More compact than deterministic FSMs v For a fixed input sequence: v A deterministic system exhibits a single behavior v A non-deterministic system exhibits a set of behaviors . . .

What we will be able to do with FSMs q FSMs provide: v A way to represent the system for: Ø Mathematical analysis Ø So that a computer program can manipulate it v A way to model the environment of a system. v A way to represent what the system must do and must not do – its specification. v A way to check whether the system satisfies its specification in its operating environment.

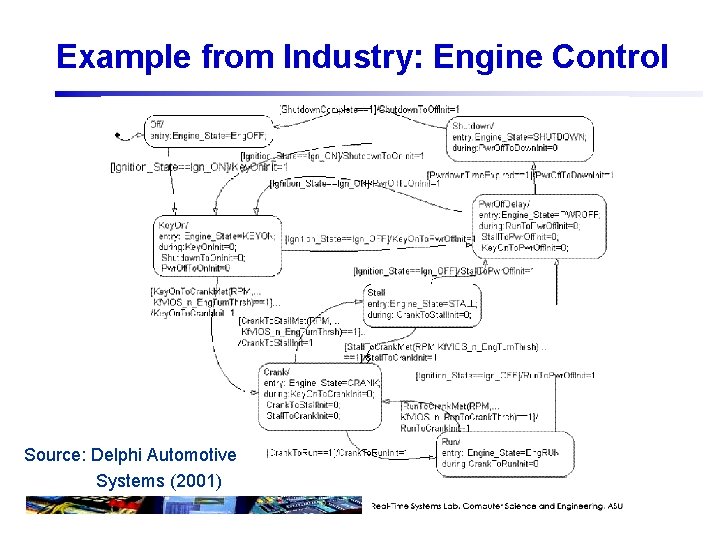
Example from Industry: Engine Control Source: Delphi Automotive Systems (2001)

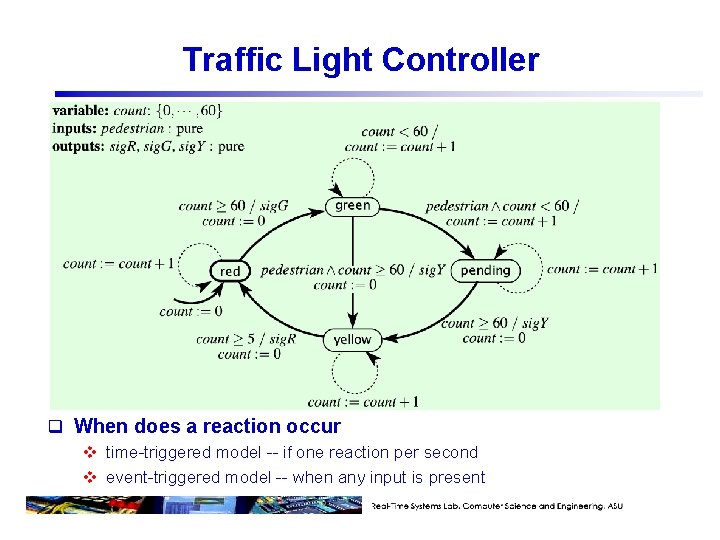
Traffic Light Controller q When does a reaction occur v time-triggered model -- if one reaction per second v event-triggered model -- when any input is present