CSE 471 Project 3 Regression Planner using A

CSE 471 -Project 3 Regression Planner using A* Sreelakshmi Vaddi

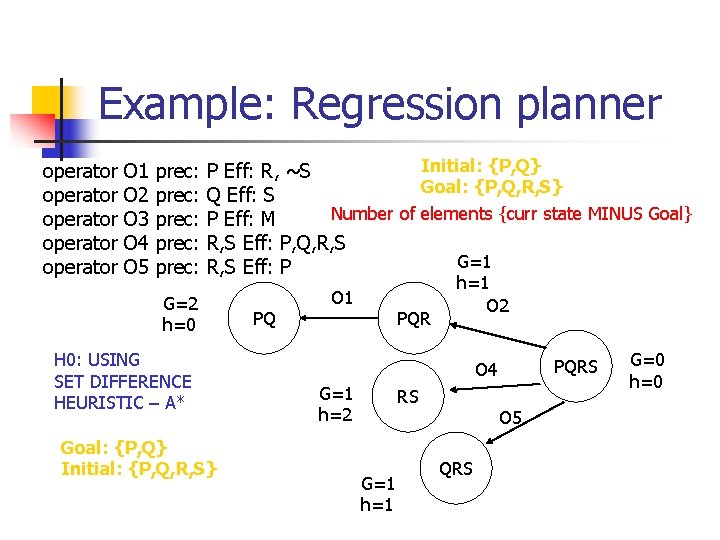
Example: Regression planner operator operator O 1 O 2 O 3 O 4 O 5 prec: prec: Initial: {P, Q} P Eff: R, ~S Goal: {P, Q, R, S} Q Eff: S Number of elements {curr state MINUS Goal} P Eff: M R, S Eff: P, Q, R, S G=1 R, S Eff: P G=2 h=0 H 0: USING SET DIFFERENCE HEURISTIC – A* Goal: {P, Q} Initial: {P, Q, R, S} PQ O 1 PQR h=1 O 2 PQRS O 4 G=1 h=2 RS G=1 h=1 O 5 QRS G=0 h=0

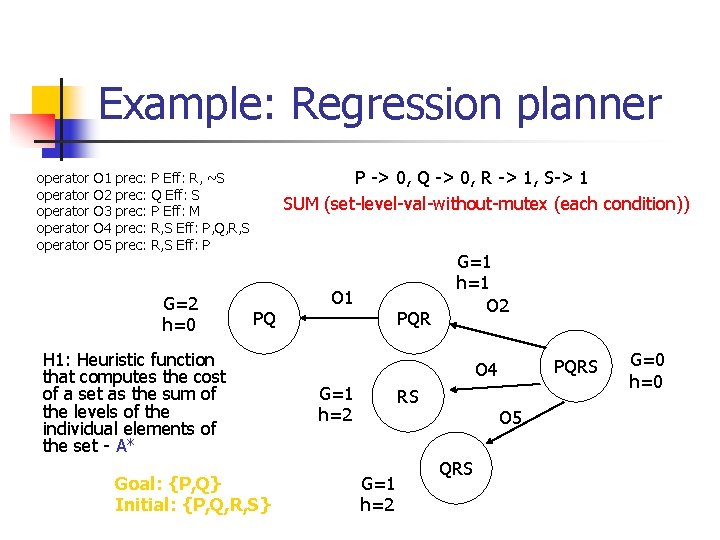
Example: Regression planner operator operator O 1 O 2 O 3 O 4 O 5 prec: prec: P -> 0, Q -> 0, R -> 1, S-> 1 SUM (set-level-val-without-mutex (each condition)) P Eff: R, ~S Q Eff: S P Eff: M R, S Eff: P, Q, R, S Eff: P G=2 h=0 PQ H 1: Heuristic function that computes the cost of a set as the sum of the levels of the individual elements of the set - A* Goal: {P, Q} Initial: {P, Q, R, S} O 1 PQR G=1 h=1 O 2 PQRS O 4 G=1 h=2 RS G=1 h=2 O 5 QRS G=0 h=0

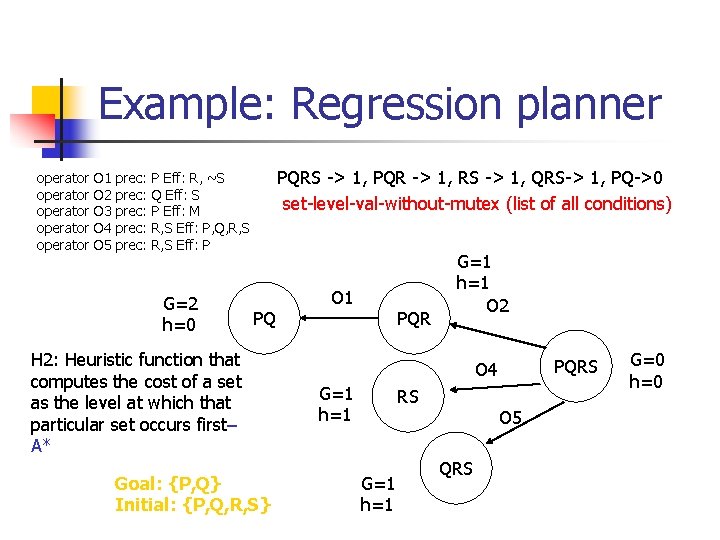
Example: Regression planner operator operator O 1 O 2 O 3 O 4 O 5 prec: prec: PQRS -> 1, PQR -> 1, RS -> 1, QRS-> 1, PQ->0 set-level-val-without-mutex (list of all conditions) P Eff: R, ~S Q Eff: S P Eff: M R, S Eff: P, Q, R, S Eff: P G=2 h=0 PQ H 2: Heuristic function that computes the cost of a set as the level at which that particular set occurs first– A* Goal: {P, Q} Initial: {P, Q, R, S} O 1 PQR G=1 h=1 O 2 PQRS O 4 G=1 h=1 RS G=1 h=1 O 5 QRS G=0 h=0

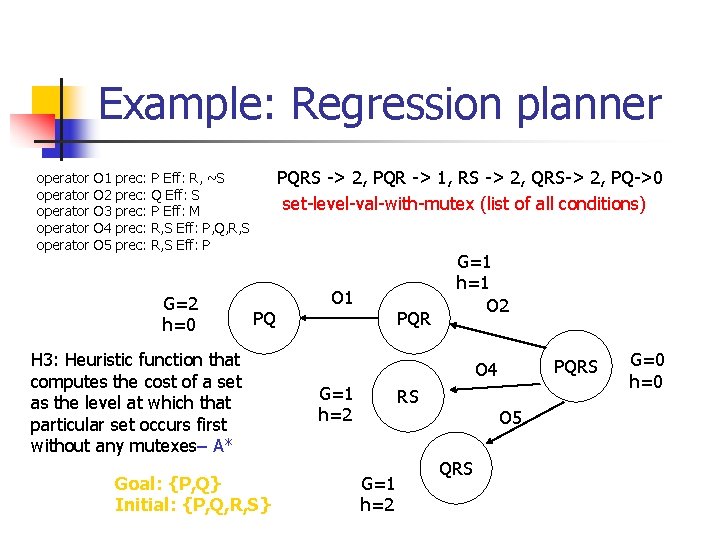
Example: Regression planner operator operator O 1 O 2 O 3 O 4 O 5 prec: prec: PQRS -> 2, PQR -> 1, RS -> 2, QRS-> 2, PQ->0 set-level-val-with-mutex (list of all conditions) P Eff: R, ~S Q Eff: S P Eff: M R, S Eff: P, Q, R, S Eff: P G=2 h=0 PQ H 3: Heuristic function that computes the cost of a set as the level at which that particular set occurs first without any mutexes– A* Goal: {P, Q} Initial: {P, Q, R, S} O 1 PQR G=1 h=1 O 2 PQRS O 4 G=1 h=2 RS G=1 h=2 O 5 QRS G=0 h=0

What you need to get started n Load the code given to you on Allegro n n n You need not touch/modify this code at all Loading instructions on project webpage : problems file + graph plan code You will need from Project 1 – A* search n n n n Node structure Children function A* main function Trace path Display stats part Puzzle children F-value fn NEW FUNCTIONS: Heuristics: H 0, H 1, H 2, H 3 Goalp: (Actually initialp)

Heuristics and Goalp functions H 0: Number of elements {curr state MINUS Goal} H 1: SUM (set-level-val-without-mutex (each condition)) H 2: set-level-val-without-mutex (list of all conditions) H 3: set-level-val-with-mutex (list of all conditions) Goalp: find if current state is equal to the goal state Eg: {PQR} = {PQ} FALSE

Puzzle Children Function n n Generates the children of current state, by checking if there is an operator applicable to current state When can you apply an op to state s? None of effects of op negate conditions in S (Reason why we don’t apply O 1 in Eg) n At least one effect of op is in S Negative literals (Reason why we don’t apply O 3 in Eg)Op-adds, op-deletes n And May be more conditions n

Puzzle Children Function Contd n New state generation? n op-preconditions U (parent state – op-effects) IMPORTANT: Handling negative literals n n n ‘P is (: NOT (P)) (So check car of every condition to see if its negative literal and then *special*) Op-deletes, op-adds can be useful than op-effects PQR on o 1 ? (operator O 1 prec: P Eff: R, ~S) {p} U {{p, q, r}-{r, ~s}}={p, q}

Useful functions-Graph Plan code n n n (get-ground-operators ‘Eg-problem) : returns O 1. . O 5 (op-name op 1) : returns (UNSTACK A A) (op-preconditions op 1) n n (op-effects op 1) n n ((HOLDING A) (CLEAR A) (: NOT (CLEAR A)) (: NOT (ARM-EMPTY)) (: NOT (ON A A))) (op-adds op 1) n n ((ON A A) (CLEAR A) (ARM-EMPTY)) ((HOLDING A) (CLEAR A)) (op-deletes op 1) n ((CLEAR A) (ARM-EMPTY) (ON A A))

Useful functions-Graph Plan code n (problem-init 'class-problem) : Initial state of the problem n ((OBJECT A) (OBJECT B) (ON-TABLE A) (ON-TABLE B) (CLEAR A) (CLEAR B) (ARM-EMPTY)) n (problem-goal 'class-problem) : Goal state of the problem n n n ((: NOT (CLEAR B)) (ARM-EMPTY)) Heuristic Functions (Compute-pg problem) : Has to be called in the beginning of every problem so that you can call the above functions as well as heuristic functions.

Other functions n Lisp set operations (list 1 list 2 : test #’equal) n n n Set Difference Union Intersection

Possible Program Flow n n n Call compute-gp, get-ground-operators, problem-init, problem-goal Make goal node from problem-init Call A*(list goal-node, goalp, …) n n n Change puzzle-children function as discussed above Write Goalp function Write heuristic functions calling set-level functions from the given code

Progression Planner - Simpler n When an OP can apply to state S? n n New child state n n n S contains OP-preconditions (S Union OP-effects) Rest remain same And don’t forget to change the compute-pg code part as said by Dr. Rao in project description

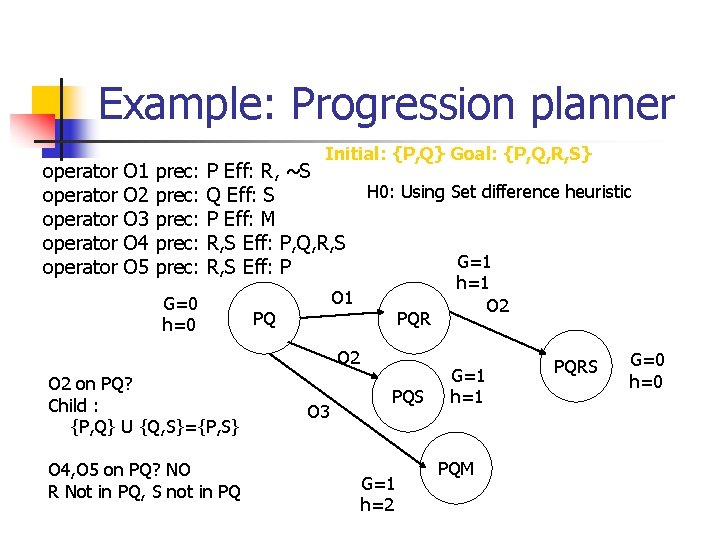
Example: Progression planner operator operator O 1 O 2 O 3 O 4 O 5 prec: prec: Initial: {P, Q} Goal: {P, Q, R, S} P Eff: R, ~S Q Eff: S P Eff: M R, S Eff: P, Q, R, S Eff: P G=0 h=0 H 0: Using Set difference heuristic O 1 PQ PQR O 2 on PQ? Child : {P, Q} U {Q, S}={P, S} O 4, O 5 on PQ? NO R Not in PQ, S not in PQ O 3 PQS G=1 h=2 G=1 h=1 O 2 G=1 h=1 PQM PQRS G=0 h=0