CSE 416 DIGITAL CONTROL Lecture 02 Sampling Reconstruction

CSE 416: DIGITAL CONTROL Lecture 02: Sampling, Reconstruction, Emulation Dr. Ahmed Mahmoud, 2/11/2020

Sampled-Data Control Systems (1) 2/11/202020 CSE 416: Digital Control, Lec 02 2

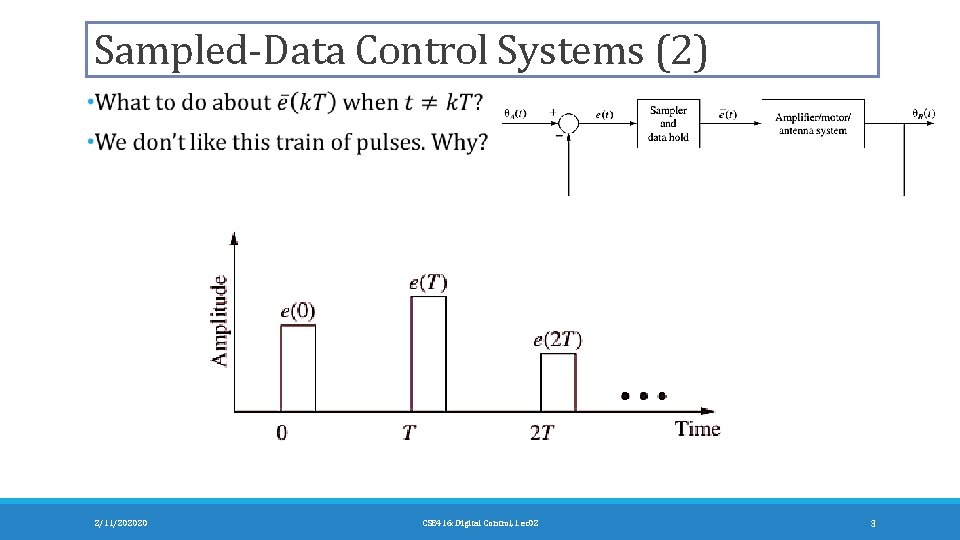
Sampled-Data Control Systems (2) 2/11/202020 CSE 416: Digital Control, Lec 02 3

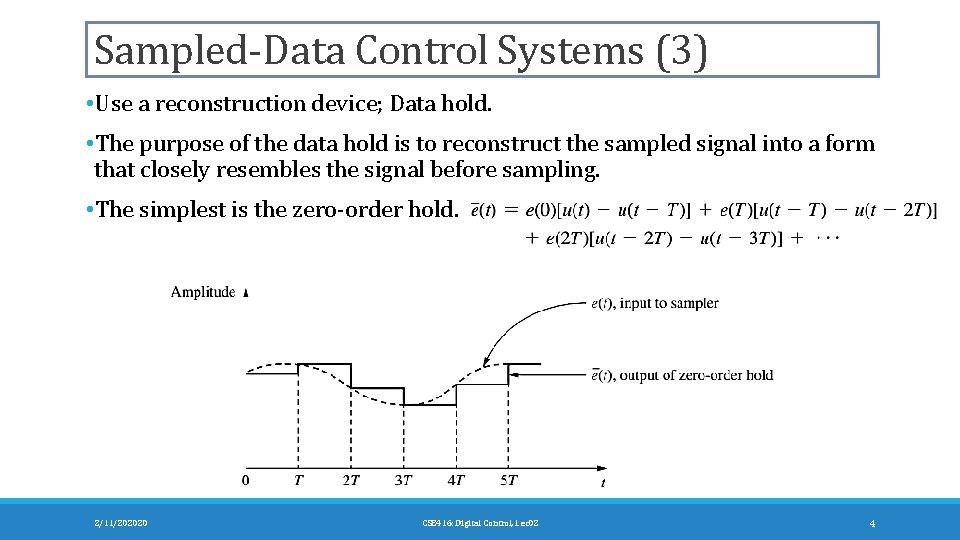
Sampled-Data Control Systems (3) • Use a reconstruction device; Data hold. • The purpose of the data hold is to reconstruct the sampled signal into a form that closely resembles the signal before sampling. • The simplest is the zero-order hold. 2/11/202020 CSE 416: Digital Control, Lec 02 4

Sampler and Zero-Order Hold • The Laplace transform of the error function after the sample and hold: • The starred function: 2/11/202020 CSE 416: Digital Control, Lec 02 5

2/11/202020 CSE 416: Digital Control, Lec 02 6

The Ideal Sampler 2/11/202020 CSE 416: Digital Control, Lec 02 7

Definition of Sampler/Hold Operation • The output signal of the ideal sampler: • The zero-order hold transfer function: • The correct sampler/hold function is modelled by: 2/11/202020 CSE 416: Digital Control, Lec 02 8

2/11/202020 CSE 416: Digital Control, Lec 02 9

2/11/202020 CSE 416: Digital Control, Lec 02 10

2/11/202020 CSE 416: Digital Control, Lec 02 11

2/11/202020 CSE 416: Digital Control, Lec 02 12

Results from Fourier Transform 2/11/202020 CSE 416: Digital Control, Lec 02 13

2/11/202020 CSE 416: Digital Control, Lec 02 14

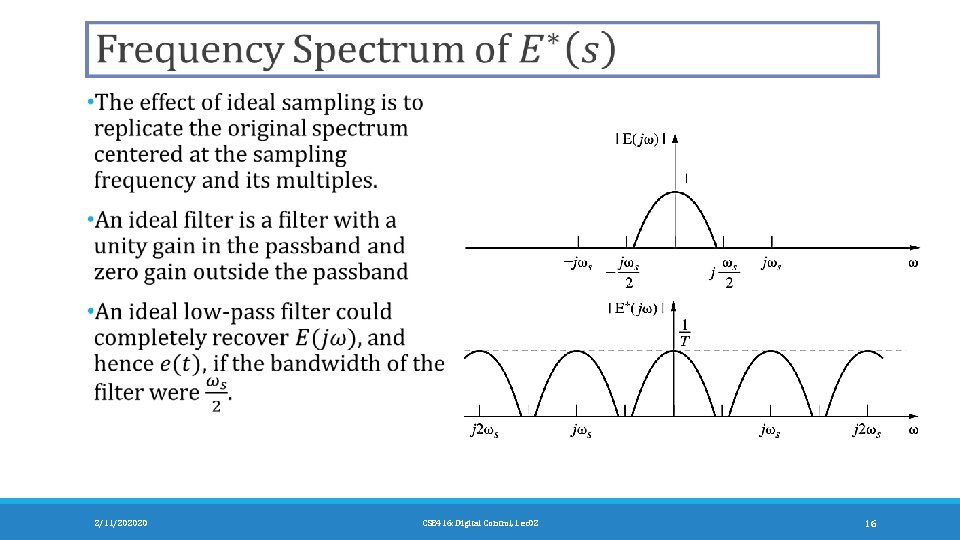
2/11/202020 CSE 416: Digital Control, Lec 02 15

2/11/202020 CSE 416: Digital Control, Lec 02 16

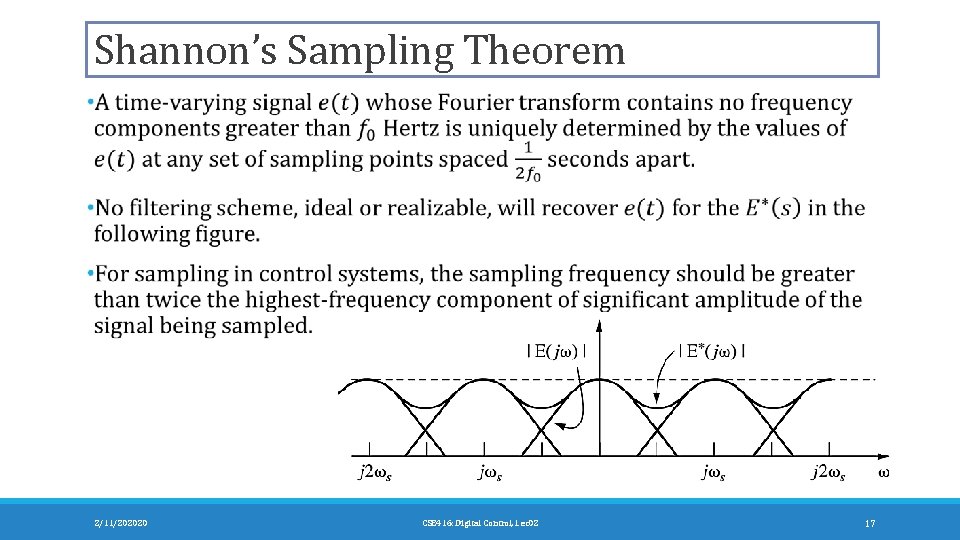
Shannon’s Sampling Theorem 2/11/202020 CSE 416: Digital Control, Lec 02 17

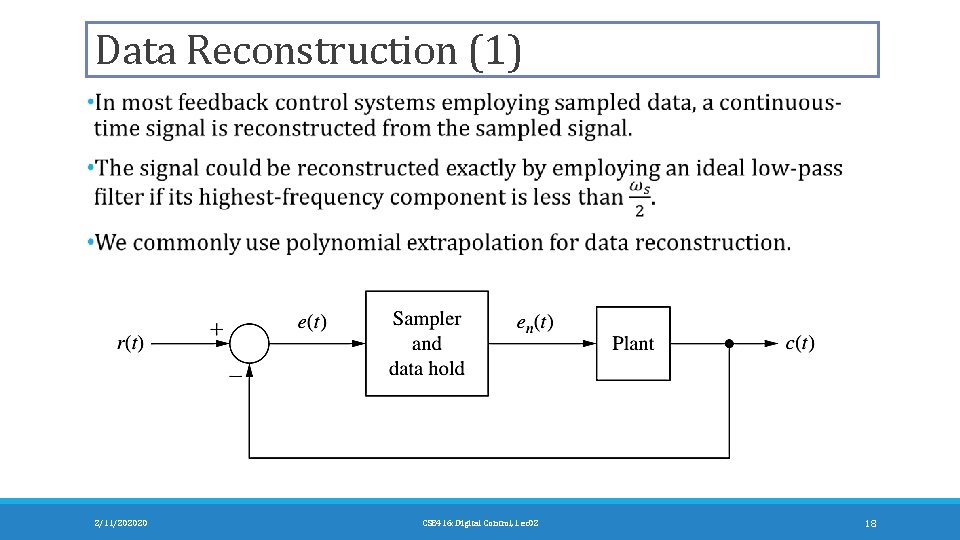
Data Reconstruction (1) 2/11/202020 CSE 416: Digital Control, Lec 02 18

Data Reconstruction (2) 2/11/202020 CSE 416: Digital Control, Lec 02 19

Zero-Order Hold 2/11/202020 CSE 416: Digital Control, Lec 02 20

• Example: 2/11/202020 CSE 416: Digital Control, Lec 02 21

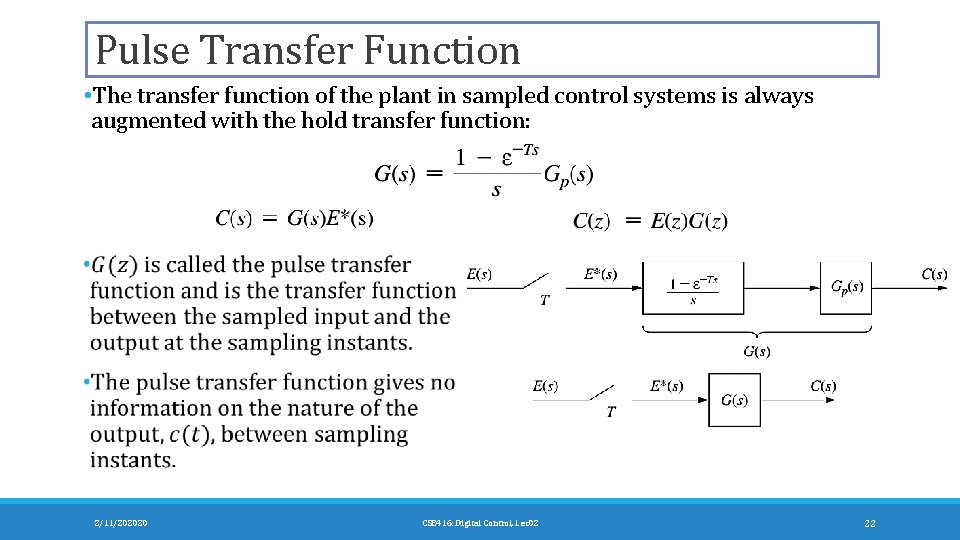
Pulse Transfer Function • The transfer function of the plant in sampled control systems is always augmented with the hold transfer function: 2/11/202020 CSE 416: Digital Control, Lec 02 22

Starred Function Derivations (1) • Given any function as: • Hence, 2/11/202020 CSE 416: Digital Control, Lec 02 23

Starred Function Derivations (2) • Example: Find the Z transform of: 2/11/202020 CSE 416: Digital Control, Lec 02 24

Starred Block Diagrams (1) 2/11/202020 CSE 416: Digital Control, Lec 02 25

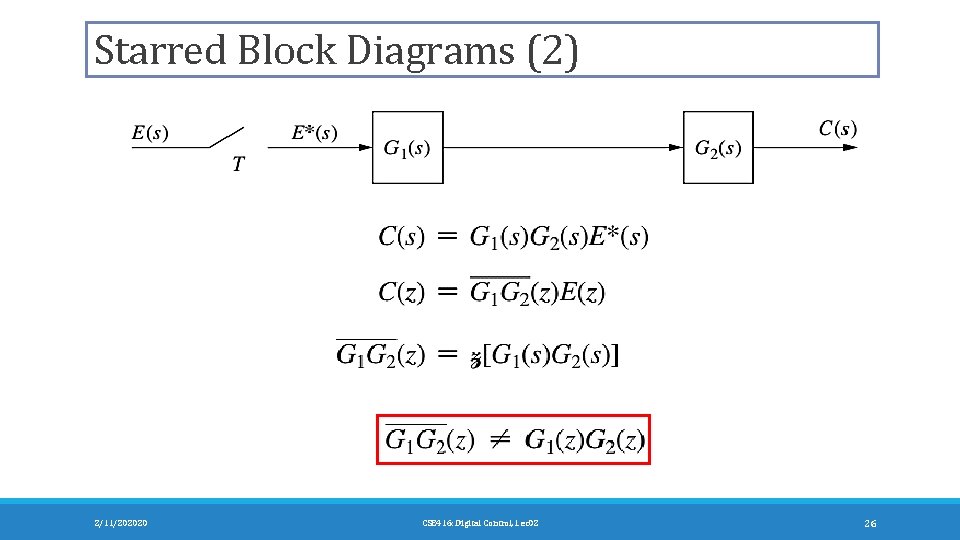
Starred Block Diagrams (2) 2/11/202020 CSE 416: Digital Control, Lec 02 26

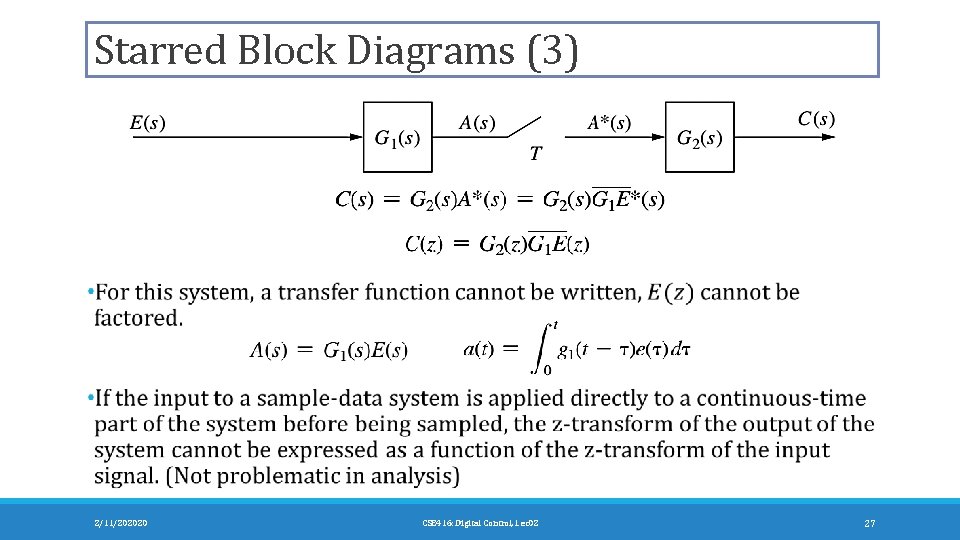
Starred Block Diagrams (3) 2/11/202020 CSE 416: Digital Control, Lec 02 27

Controller Emulation 2/11/202020 CSE 416: Digital Control, Lec 02 28

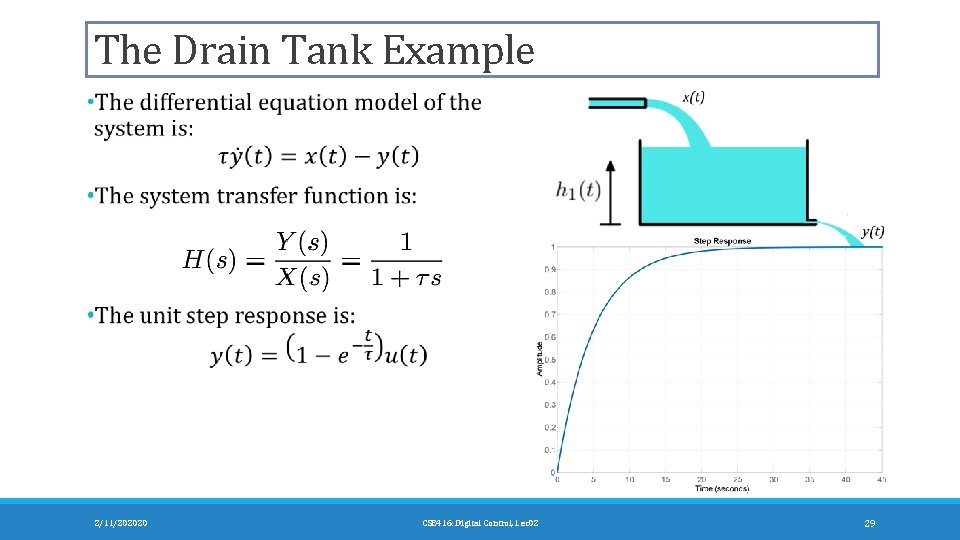
The Drain Tank Example 2/11/202020 CSE 416: Digital Control, Lec 02 29

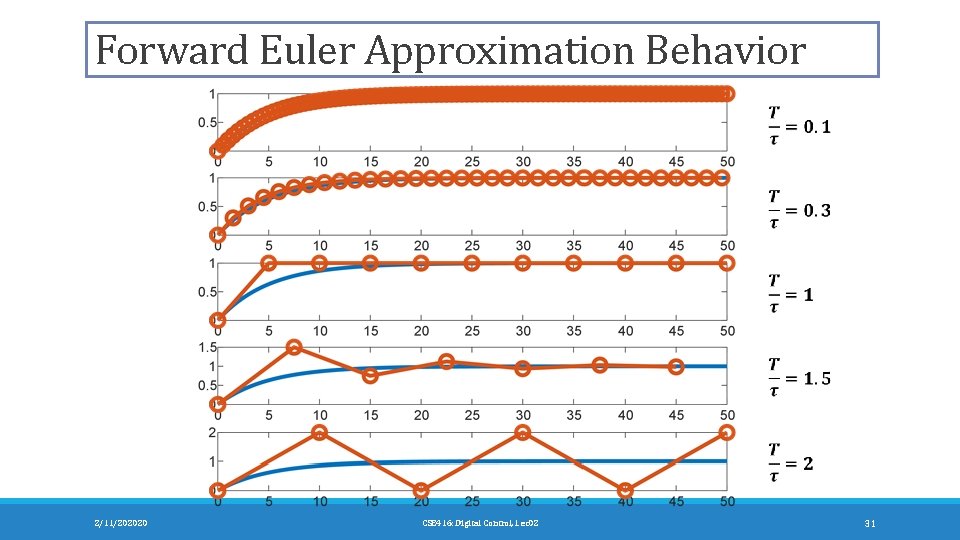
Forward Euler Approximation • Forward Euler rule approximate derivate by: • Approximate the drain tank DE: • The approximated difference equation model is: 2/11/202020 CSE 416: Digital Control, Lec 02 30

Forward Euler Approximation Behavior 2/11/202020 CSE 416: Digital Control, Lec 02 31

Z-Transform of Forward Euler 2/11/202020 CSE 416: Digital Control, Lec 02 32

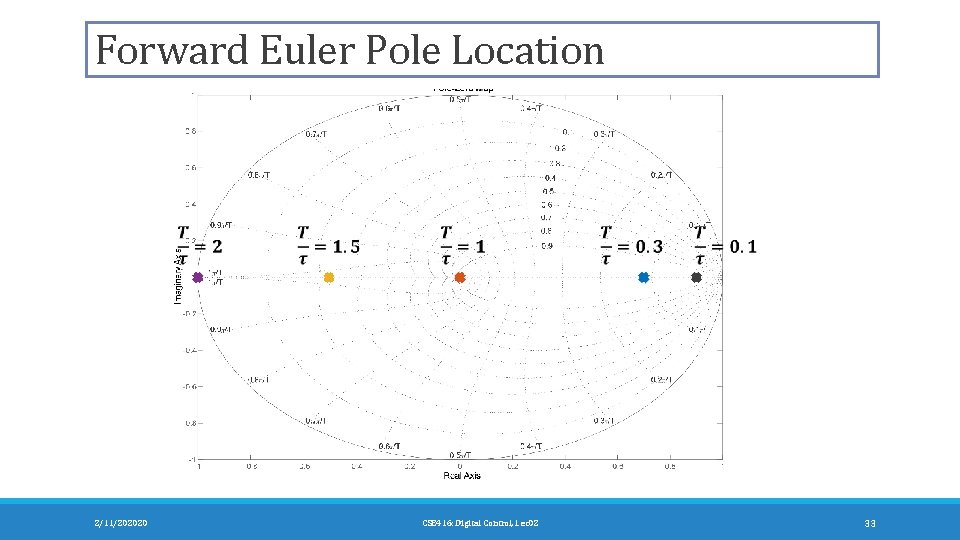
Forward Euler Pole Location 2/11/202020 CSE 416: Digital Control, Lec 02 33

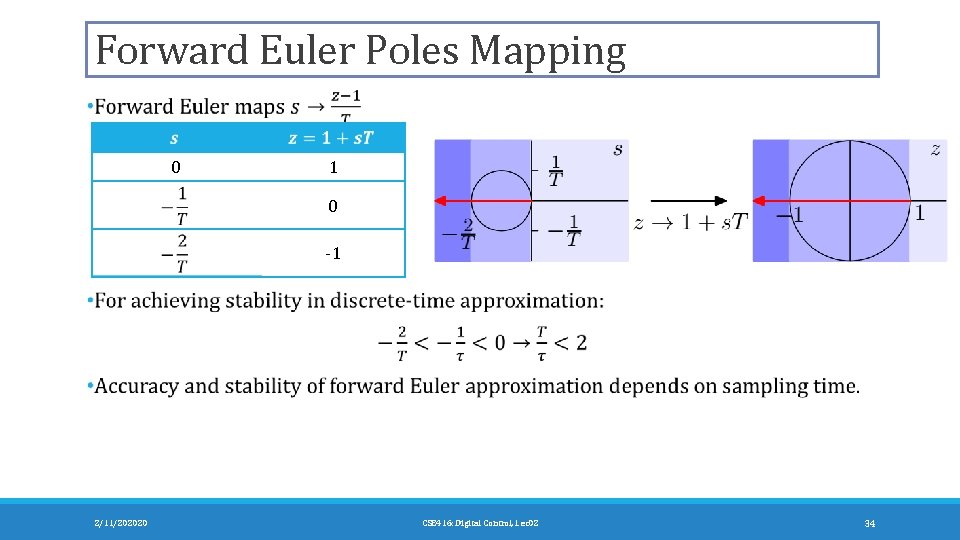
Forward Euler Poles Mapping 0 1 0 -1 2/11/202020 CSE 416: Digital Control, Lec 02 34

Backward Euler Approximation • Backward Euler rule approximates derivate by: • Approximate the drain tank DE: • The approximated difference equation model is: 2/11/202020 CSE 416: Digital Control, Lec 02 35

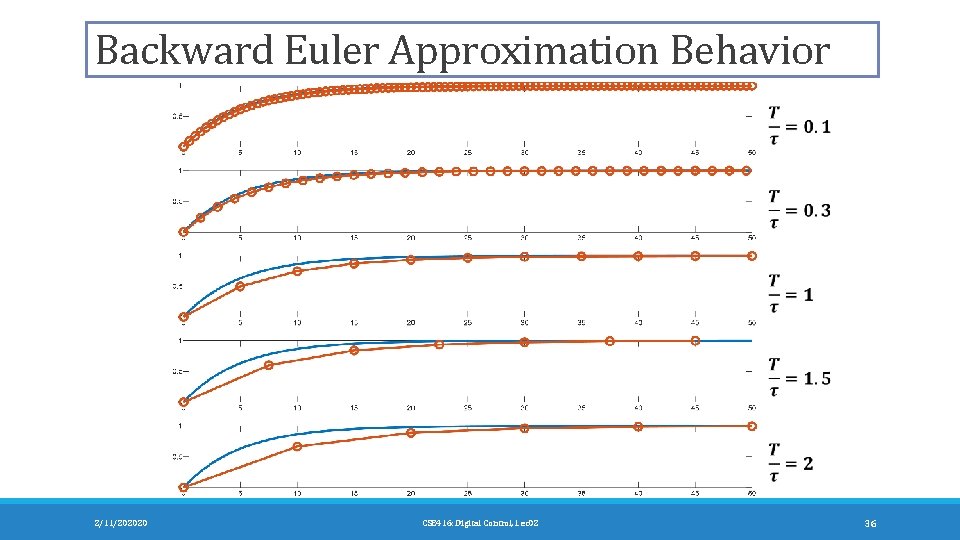
Backward Euler Approximation Behavior 2/11/202020 CSE 416: Digital Control, Lec 02 36

Z-Transform of Backward Euler 2/11/202020 CSE 416: Digital Control, Lec 02 37

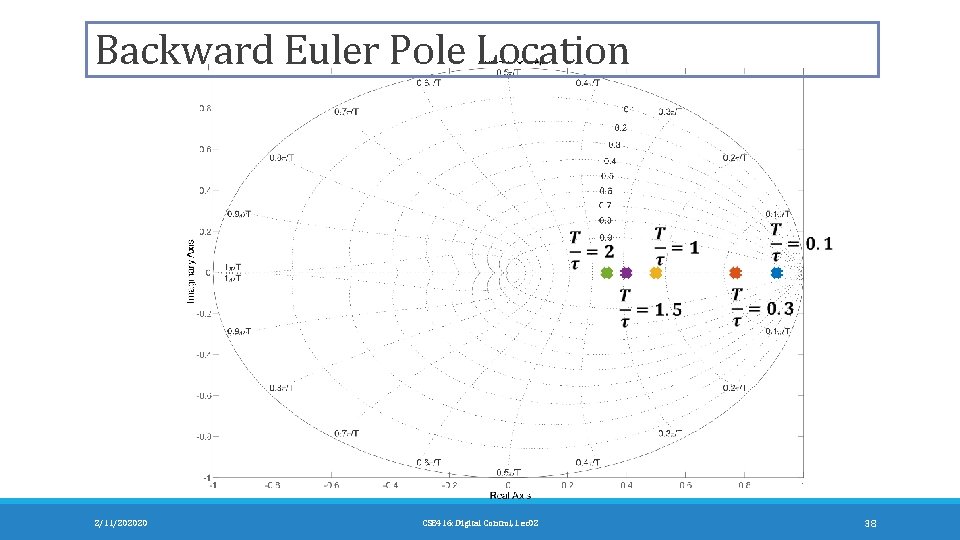
Backward Euler Pole Location 2/11/202020 CSE 416: Digital Control, Lec 02 38

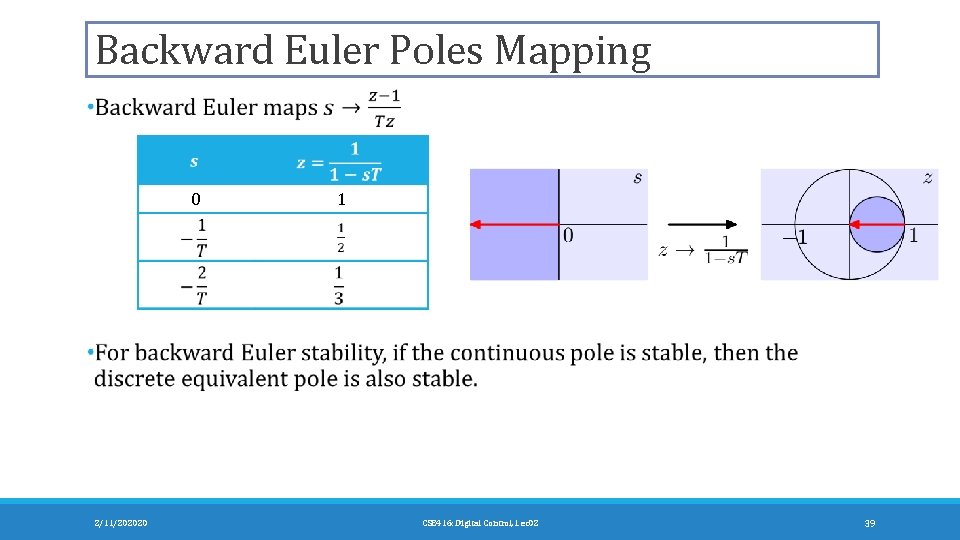
Backward Euler Poles Mapping 0 2/11/202020 1 CSE 416: Digital Control, Lec 02 39

Trapezoidal Rule (Tustin Transformation) 2/11/202020 CSE 416: Digital Control, Lec 02 40

Which to Use for Implementation? • Forward (explicit) Euler approach is numerically not efficient. • Complex algorithms designed for efficient numerical integration are not applicable to real-time control systems. • Tustin transformation is often used in practice to produce a satisfactory closed-loop system behavior. 2/11/202020 CSE 416: Digital Control, Lec 02 41

Example: Emulation of a Lead Controller 2/11/202020 CSE 416: Digital Control, Lec 02 42

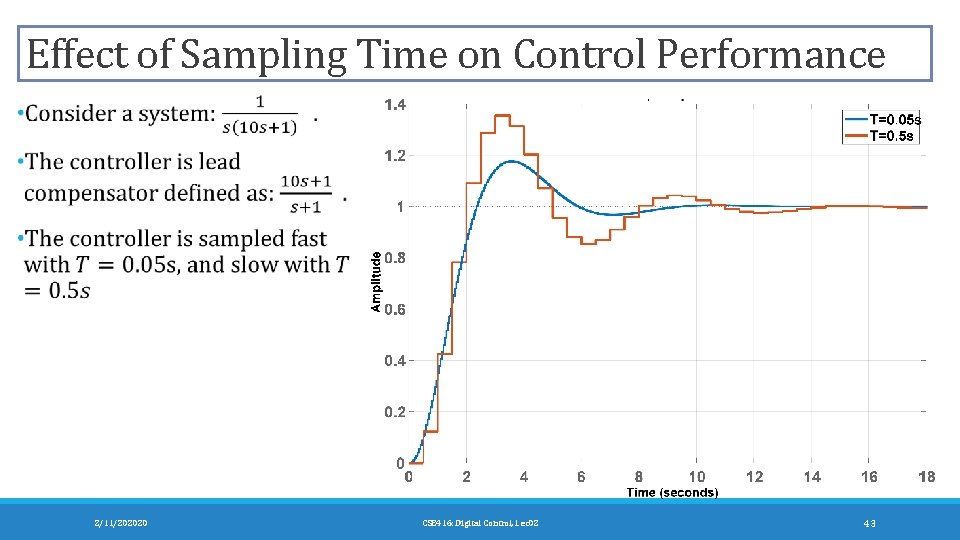
Effect of Sampling Time on Control Performance 2/11/202020 CSE 416: Digital Control, Lec 02 43

Reading • Read Chapter 3. • Read Sections 4. 1 to 4. 4. 2/11/202020 CSE 416: Digital Control, Lec 02 44