CSE 4095 Assymmetric Cryptography 8 1 Recall symmetric

CSE 4095 Assymmetric Cryptography 8 -1

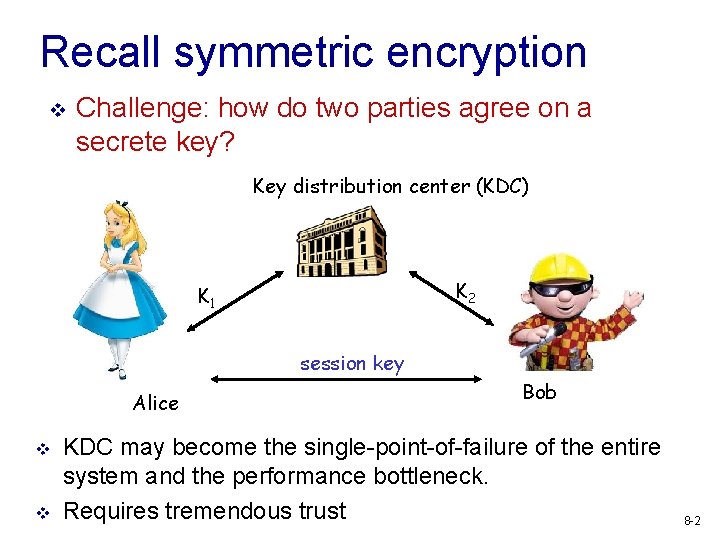
Recall symmetric encryption v Challenge: how do two parties agree on a secrete key? Key distribution center (KDC) K 2 K 1 session key Alice v v Bob KDC may become the single-point-of-failure of the entire system and the performance bottleneck. Requires tremendous trust 8 -2

Why Public-Key Cryptography? v Two difficult problems associated with symmetric cipher: v § Key distribution: How to have secure communications in general without having to trust a KDC with your key? § Digital signature: How to verify that a message comes intact from the claimed sender Whitfield Diffie and Martin Hellman, “New directions in cryptography”, 1976 8 -3

Public Key Cryptography idea symmetric key crypto v requires sender, receiver know shared secret key Should not be obvious that this exists!!! public key crypto radically different v sender, receiver do not share secret key v public encryption key known to all v private decryption key known only to receiver v 8 -4

Public-Key Cryptography v involves the use of two keys: § public-key, which may be known by anybody, and can be used to encrypt messages, and verify signatures § private-key, known only to the recipient, used to decrypt messages, and sign (create) signatures v is asymmetric because § those who encrypt messages or verify signatures cannot decrypt messages or create signatures 8 -5

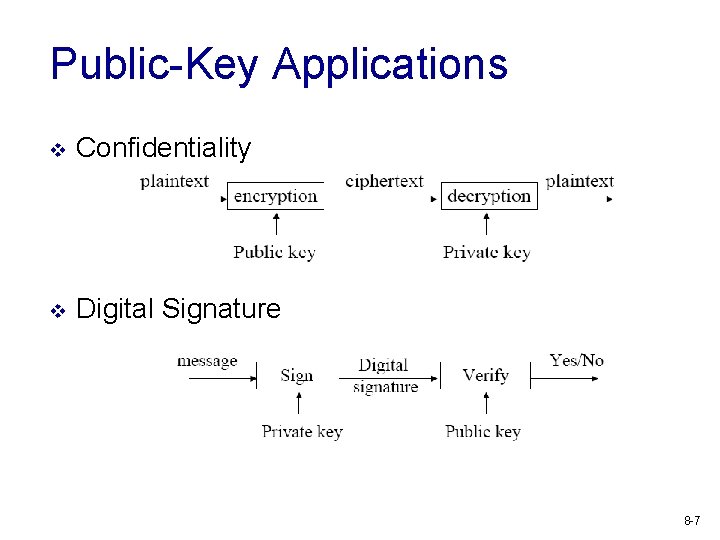
Public-Key Crypto Applications v Encryption/decryption (provide confidentiality) v Digital signatures (provide authentication) v Key exchange (of session keys) v Exercise: how? 8 -6

Public-Key Applications v Confidentiality v Digital Signature 8 -7

Hosting a website using public key cryptography v v v Suppose I host a website and I want my clients communication to be private and integrity protection How do I go about this? Assuming “perfect” cryptography, what problems remain? 8 -8

Public-Key Requirements v v v Computationally easy for a party B to generate a pair (public-key pkb, secret key skb) Computationally easy for a sender A, knowing pkb and m, to generate ciphertext c Computationally easy for B to decrypt c using the skb to recover m Computationally infeasible for an adversary, knowing pkb, to determine skb Computationally infeasible for an adversary, knowing the pkb and c, to learn about m 8 -9

Public-Key Cryptanalysis v Brute-force attack § Countermeasure: use large keys § Key size must be small enough to be practical § Public-key encryption is usually used to setup symmetric keys between parties v Compute the private key given the public key § To date not mathematically proven that this form of attack is infeasible for a particular public-key algorithm (relies on math problems believed to be hard) 8 -10

Rivest-Shamir-Adleman (RSA) Scheme v Developed in 1977 at MIT by Ron Rivest, Adi Shamir & Leonard Adleman § “A Method for Obtaining Digital Signatures and Public. Key Cryptosystems, ” Communications of the ACM, Feb. 1978 v Most widely used public-key encryption v plaintext and ciphertext are integers between 0 and n – 1 for some n § typical size for n: 2048 bits, or 618 decimal digits 8 -11

Prerequisite: modular arithmetic v v x mod n = remainder of x when divide by n facts: [(a mod n) + (b mod n)] mod n = (a+b) mod n [(a mod n) - (b mod n)] mod n = (a-b) mod n [(a mod n) * (b mod n)] mod n = (a*b) mod n v thus (a mod n)d mod n = ad mod n 8 -12

Mod Arithmetic (consider mod 11) x 3 x x 3 1 2 3 4 5 6 7 8 9 10 8 -13

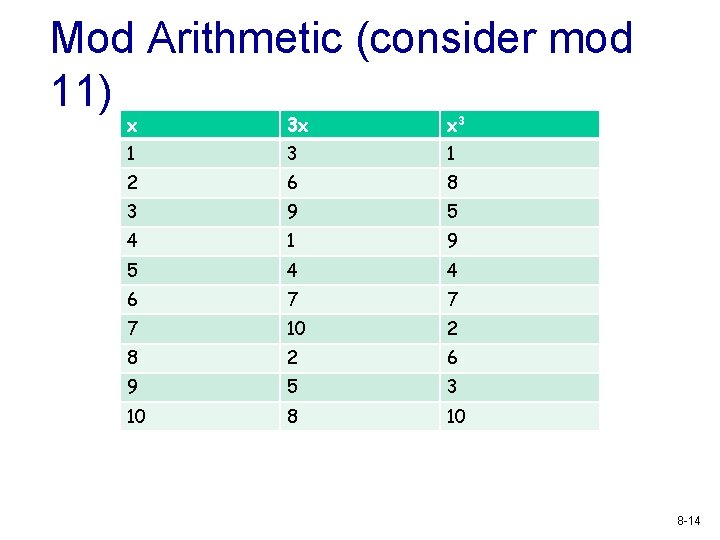
Mod Arithmetic (consider mod 11) x 3 x x 3 1 2 6 8 3 9 5 4 1 9 5 4 4 6 7 7 7 10 2 8 2 6 9 5 3 10 8 -14

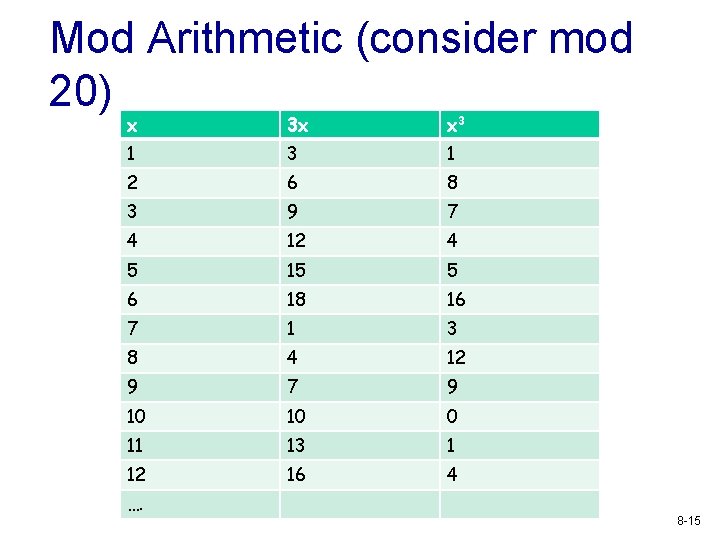
Mod Arithmetic (consider mod 20) x 3 x x 3 1 2 6 8 3 9 7 4 12 4 5 15 5 6 18 16 7 1 3 8 4 12 9 7 9 10 10 0 11 13 1 12 16 4 …. 8 -15

RSA: getting ready v v v message: just a bit pattern can be uniquely represented by an integer number encrypting a message is encrypting a number. example: v v m= 10010001. This message is uniquely represented by the decimal number 145. to encrypt m, we encrypt the corresponding number, which gives a new number (i. e. , ciphertext). 8 -16

RSA: Creating public/private key pair 1. choose two large prime numbers p, q. (e. g. , 1024 bits each) 2. compute n = pq, z = (p-1)(q-1) 3. choose e (with e<n) that has no common factors with z (e, z are “relatively prime”). 4. choose d such that ed-1 is exactly divisible by z. (in other words: ed mod z = 1 ). 5. public key is (n, e). private key is (n, d). 8 -17

RSA: encryption, decryption 0. given (n, e) and (n, d) as computed above 1. to encrypt message m (<n), compute c = me mod n 2. to decrypt received bit pattern, c, compute m = cd mod n magic m = (me mod n) d mod n happens! c 8 -18

RSA example: Bob chooses p=5, q=7. Then n=35, z=24. e=5 (so e, z relatively prime). d=29 (so ed-1 exactly divisible by z). encrypting 8 -bit messages. encrypt: decrypt: bit pattern m me 0000 ll 00 12 24832 c 17 c d 48196857210675091411825223071697 c = me mod n 17 m = cd mod n 12 8 -19

Why does RSA work? v v must show that cd mod n = m where c = me mod n fact: for any x and y: xy mod n = x(y mod z) mod n § where n= pq and z = (p-1)(q-1) v thus, cd mod n = (me mod n)d mod n = med mod n = m(ed mod z) mod n = m 1 mod n =m 8 -20

Recall our definitions of security v Possible goals: § Determine which of two messages was sent § Recover key § Change message being sent § Make message unreadable v Possible capabilities: § See a single ciphertext § See ciphertexts and know plaintext § Choose plaintexts and see ciphertext § Choose plaintext adaptively and see ciphertext § Create ciphertexts and see if decryption works 8 -21

Exercise v v Assuming we don’t know how to factor numbers Assume we aren’t cryptanalysts (if you are great) What kind of security do you think RSA provides? What kind of security does it not provide? 8 -22

Efficient Operation Using the Public Key v Use specific e v The most common choice is 65537 (216 + 1) § Two other popular choices are e=3 and e=17 § Each of these choices has only two 1 bits, so the number of multiplications required to perform exponentiation is minimized § With a very small public key, such as e = 3, RSA becomes vulnerable to a simple attack 8 -26

Efficient Operation Using the Private Key v Decryption uses exponentiation to power d § A small value of d is vulnerable to a bruteforce attack and to other forms of cryptanalysis v Can use the Chinese Remainder Theorem (CRT) to speed up computation § The quantities d mod (p – 1) and d mod (q – 1) can be precalculated § End result is that the calculation is approximately four times as fast as 8 -27

Key Generation v v Determine two prime numbers p and q Select either e or d and calculate the other v Because the value of n = pq will be known to any potential adversary, primes must be chosen from a sufficiently large set § The method used for finding large primes must be reasonably efficient 8 -28

Procedure for Picking a Prime Number v v Pick an odd integer m at random Pick an integer a < m at random Perform the probabilistic primality test with a as a parameter. If m fails the test, reject the value m and go to step 1 If m has passed a sufficient number of tests, accept m; otherwise, go to step 2 8 -29

Using RSA v Use “safe” primes p and q. p-1 and q-1 should have large prime factors. v p and q should not have the same number of digits. v e cannot be too small v Don’t use same n for different e’s. v You should always “pad”: remove structure in m (padding scheme called OEAP) RSA is complicated!!! Don’t implement it yourself!!! 8 -30

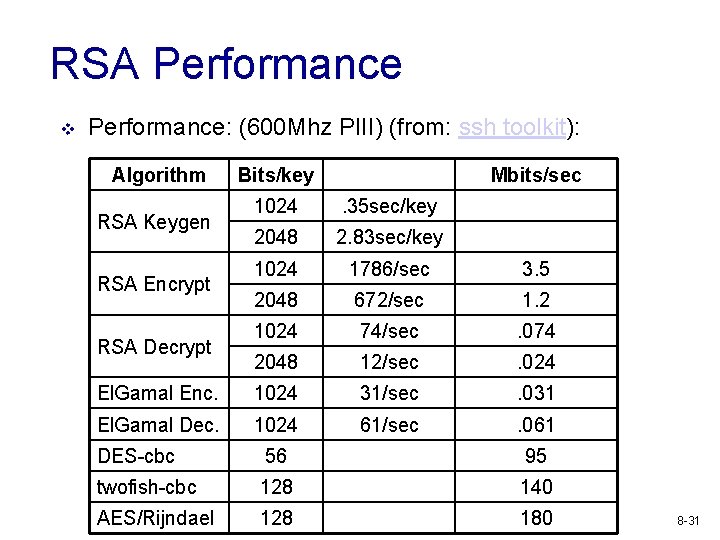
RSA Performance v Performance: (600 Mhz PIII) (from: ssh toolkit): Algorithm Bits/key Mbits/sec 1024 . 35 sec/key 2048 2. 83 sec/key 1024 1786/sec 3. 5 2048 672/sec 1. 2 1024 74/sec . 074 2048 12/sec . 024 El. Gamal Enc. 1024 31/sec . 031 El. Gamal Dec. 1024 61/sec . 061 RSA Keygen RSA Encrypt RSA Decrypt DES-cbc 56 95 twofish-cbc 128 140 AES/Rijndael 128 180 8 -31

Security of RSA v Brute force attack: try all the keys v Mathematic attack: all involve factoring v Timing attack v Chosen ciphertext attack: choose special ciphertext v Hardware fault-based attack 8 -32

Mathematical attack: factoring v Factor n into its two prime factors. This enables calculation of ø(n) = (p – 1)(q – 1), which in turn enables determination of d = e-1 (mod ø(n)) v Determine ø(n) directly without first determining p and q. Again this enables determination of d = e-1 (mod ø(n)) v Determine d directly without first determining ø(n) 8 -33

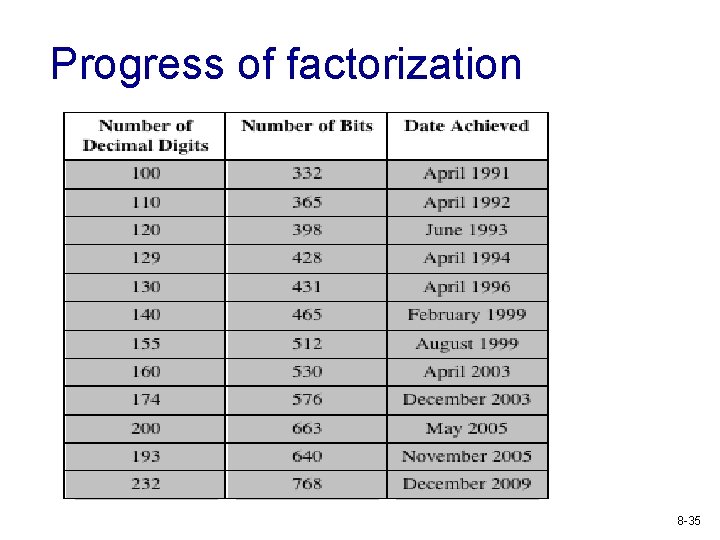
Factoring in the Real World v Quadratic Sieve (QS): v § log n bits in input, superpolynomial time § Used in 1994 to factor a 129 digit (428 -bit) number. 1600 Machines, 8 months. Number field Sieve (NFS): § Used in 1999 to factor 155 digit (512 -bit) number. 35 CPU years. At least 4 x faster than QS § Used in 2003 -2005 to factor 200 digits (663 bits) 75 CPU years ($20 K prize) 8 -34

Progress of factorization 8 -35

RSA Status v v v 1024 bit modulus is nearing end of life RSA has grown increasingly complicated to use (parameters need to be chosen more carefully) If a quantum computer is built it can efficiently factor large numbers § “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer” by Peter Shor 1997 8 -36

Timing Attacks v. A snooper can determine a private key by keeping track of how long a computer takes to decipher messages (by Paul Kocher) v Main idea: different operations take different amount of time v Applicable to other public-key cryptography systems 8 -37

Hardware Fault-Based Attack v An attack on a processor that is generating RSA digital signatures § Induces faults in the signature computation by reducing the power to the processor § Faults cause the software to produce invalid signatures which can then be analyzed by attacker to recover the private key v Requirements § Attacker have physical access to the target machine § Attacker is able to directly control the input power to the processor 8 -38

Public-Key Encryption: True or False v v v Public-key encryption is more secure from cryptanalysis than symmetric encryption Public-key encryption is a general-purpose technique that has made symmetric encryption obsolete Key distribution is trivial when using publickey encryption, compared to the cumbersome handshaking involved with key distribution centers for symmetric encryption 8 -39