CSE 4080 Computer Science Project Advanced Algorithm Design

CSE 4080 Computer Science Project Advanced Algorithm Design and Analysis Student: Supervisor: Gertruda Grolinger Prof. Jeff Edmonds

Topics: § Divide and Conquer: Fast Fourier Transformations § Recursion: Parsing § Greedy Algorithms: Matroids § Dynamic Programming: Parsing CFG § Network Flow: Steepest Assent, Edmonds-Karp, Matching § Classifying problems § NP-completeness: Reductions § Approximation Algorithms: Knapsack § Linear Programming: “What to put in a hotdog? ”

The Pebble Game

The Pebble Game • One player game, played on a DAG • Used for studying time-space trade-off

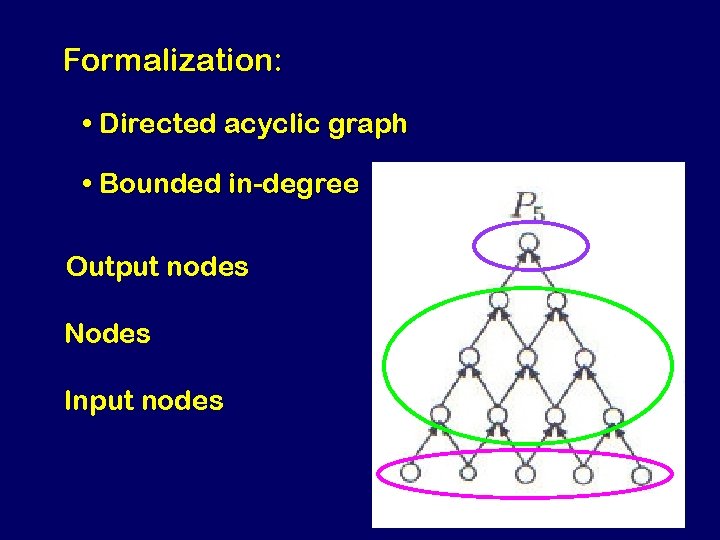
Formalization: • Directed acyclic graph • Bounded in-degree Output nodes Nodes Input nodes

Three main rules: 1. A pebble can be placed on any input node 2. A pebble can be placed on a node v if all predecessors of the node v are marked with pebbles 3. A pebble can be removed from a node at any time Note: a pebble removed from the graph can be ‘reused’

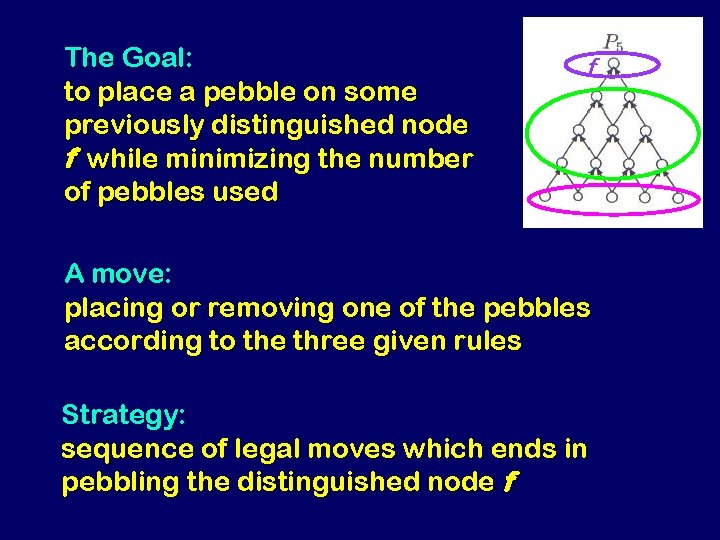
The Goal: to place a pebble on some previously distinguished node f while minimizing the number of pebbles used f A move: placing or removing one of the pebbles according to the three given rules Strategy: sequence of legal moves which ends in pebbling the distinguished node f

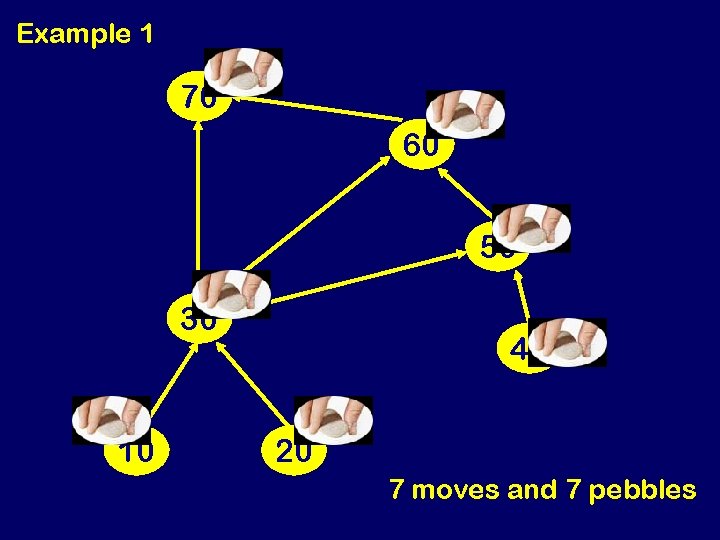
Example 1 70 60 50 30 10 40 20 7 moves and 7 pebbles

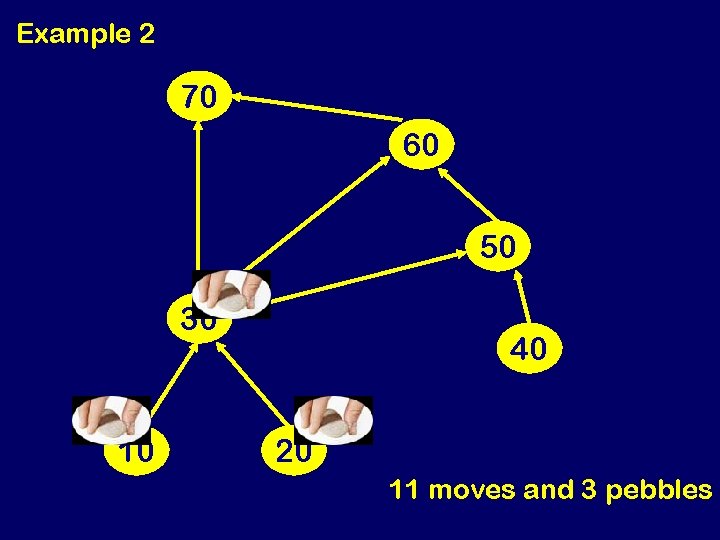
Example 2 70 60 50 30 10 40 20 11 moves and 3 pebbles

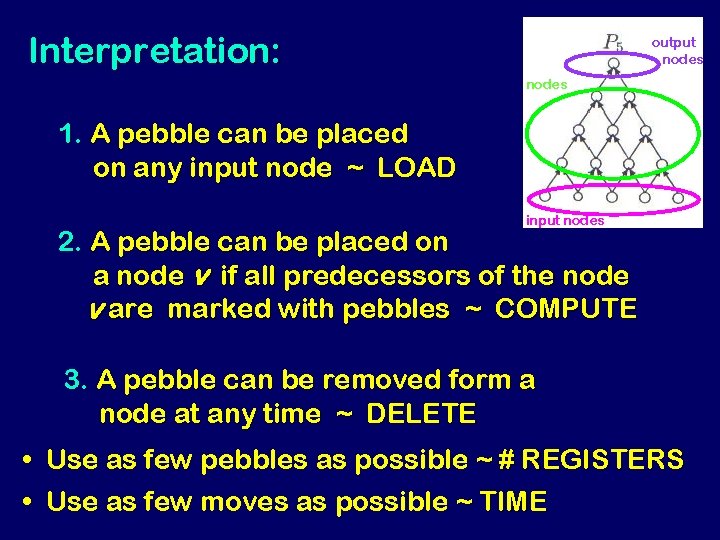
Interpretation: output nodes 1. A pebble can be placed on any input node ~ LOAD input nodes 2. A pebble can be placed on a node v if all predecessors of the node v are marked with pebbles ~ COMPUTE 3. A pebble can be removed form a node at any time ~ DELETE • Use as few pebbles as possible ~ # REGISTERS • Use as few moves as possible ~ TIME

In general: How many pebbles are required to pebble a graph with n nodes?

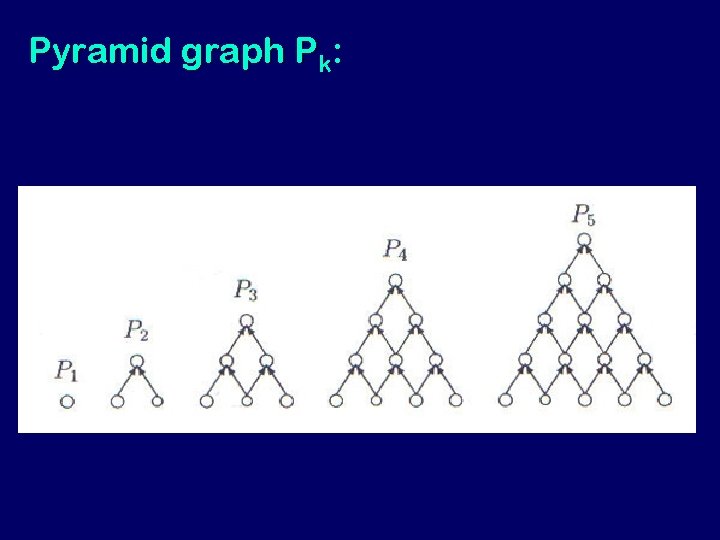
Pyramid graph Pk:

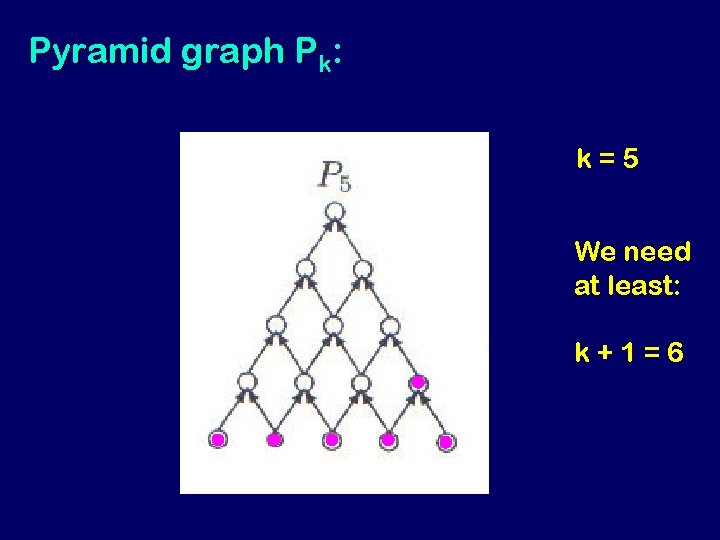
Pyramid graph Pk: Fact 1: Every pebbling strategy for Pk (k > 1) must use AT LEAST k + 1 pebbles. That is Ω( √ n ) pebbles expressed in number of edges n.

Pyramid graph Pk: k=5 We need at least: k+1=6

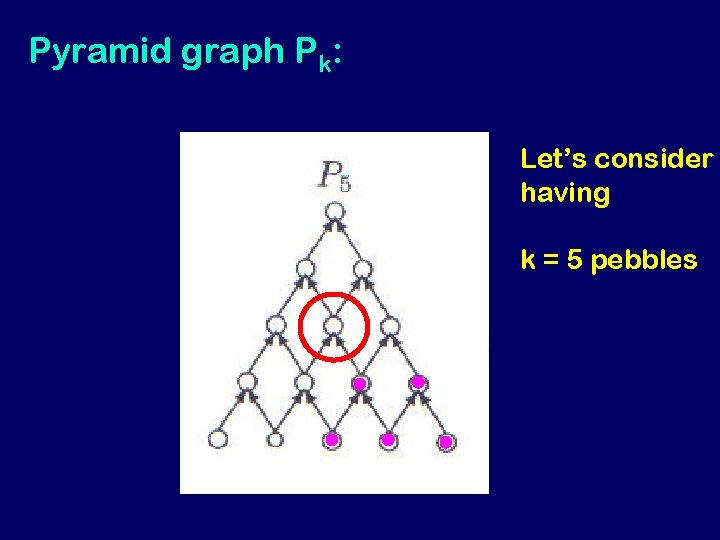
Pyramid graph Pk: Let’s consider having k = 5 pebbles

Arbitrary graph with restricted in-degree (d =2): Fact 2: Every graph of in-degree 2 can be pebbled with O(n/log n) pebbles (n = # nodes in the graph).

Arbitrary graph with restricted in-degree (d =2): O(n/log n) Proof: • Recursive pebbling strategy • Cases • Recursions for each case • Solutions: P(n) = O(n/log n)

A Pebble problem Pebble a DAG that has a rectangle of nodes that is w wide and h high (h <<w). For each node v (not on the bottom row), h d nodes In(v) = {u , …u } there will be 1 2 d on the previous row with edges to v. w v The goal is to put a pebble on any single node on the top row. u u u 1 2 … d

Dynamic Programming 1. Algorithm that uses as many pebbles (memory) as needed, but does not redo any work 2. Loop invariant 3. How much time and how many pebbles?

Dynamic Programming algorithm § Place a pebble on each of the nodes on the bottom row § After the i th iteration: there is a pebble on each node of the i th row from the bottom Loopa. Invariant § Next iteration: place pebble on each node on the (i +1)st row and remove pebbles from the i th row so they can be reused § Exit when i =h Progress made, LI maintained

Time and pebbles (space) needed § Time = O(h *w) § Pebbles = 2 *w = O(w)

Recursive Backtracking § Task: to place a pebble on some node v which is r rows from the bottom § Algorithm (recursive) to accomplish this task that re-does work but uses as few pebbles as possible § Time(r ) and Pebbles(r) are time and pebbles used to place a pebble on one node r rows from the bottom

Recursive Backtracking algorithm § My task is to place a pebble on some node v which is r rows from the bottom § I ask a friend, for each of the d nodes ui Î In(v) to place a pebble on ui § Once there is a pebble on all nodes ui Î In(v), I place a pebble on node v

Time(r ) and Pebbles(r) § Time(r) = d * Time(r-1) + 1 ≈ d * Time(r-1) = = d(r-1) § Pebbles(r ) = Pebbles(r-1) + (d – 1) = = (d - 1) * (r – 1) + 1

Conclusion: time-space trade-off § Time comparison DP: Q(h * w) RB: Q(d (h-1)) § Space comparison DP: Q(w) RB: Q(d * h) where h << w

References: 1. Gems of theoretical computer science U. Schöning, R. J. Pruim 2. Asymptotically Tight Bounds on Time-Space Trade-offs in a Pebble Game T. Lengauer, R. E. Tarjan 3. Theoretical Models 2002/03 P. van Emde Boas

Thank you for your attention Questions ?