CSE 326 Data Structures Topic 16 Multidimensional trees

CSE 326: Data Structures Topic 16: Multi-dimensional trees Luke Mc. Dowell Summer Quarter 2003

Range Query -- Remember skip lists? -- Remember homework #4? How to do this in multiple dimensions? Multi-dimension Search ADT

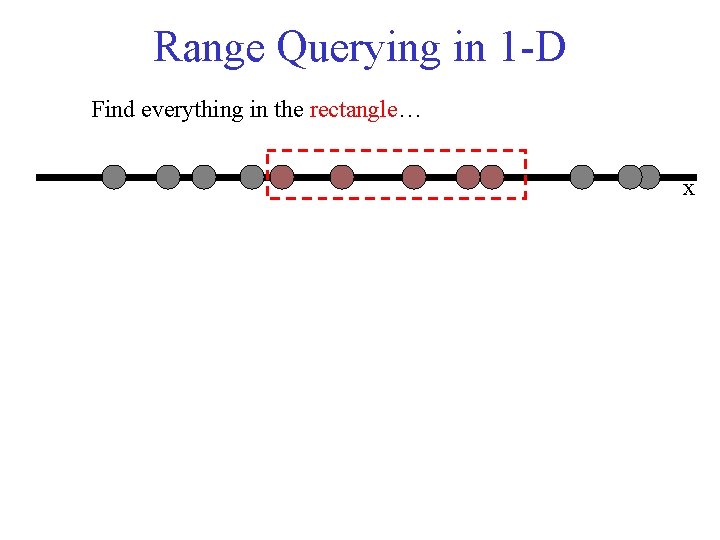
Range Querying in 1 -D Find everything in the rectangle… x

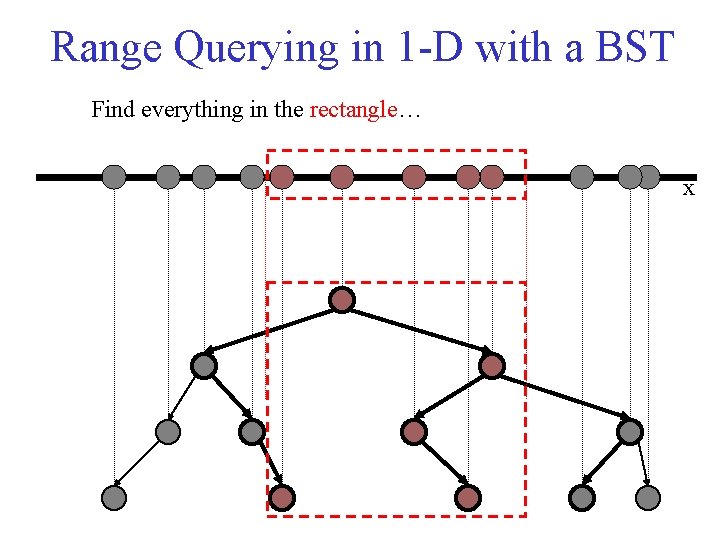
Range Querying in 1 -D with a BST Find everything in the rectangle… x

1 -D Range Query • print. Range(min, max, node) – If (in. Range () ) • Print node – If (min <= node. value) • Print (min, max, node. left) – If (max >= node. value) • Print (min, max, node. right)

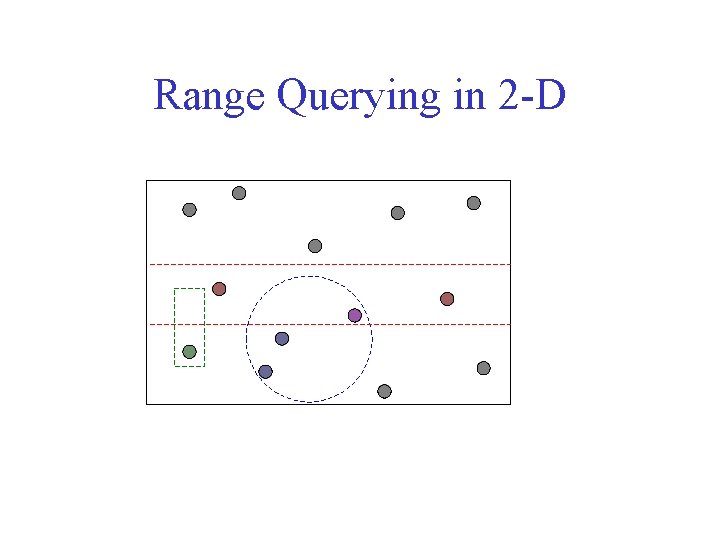
Range Querying in 2 -D

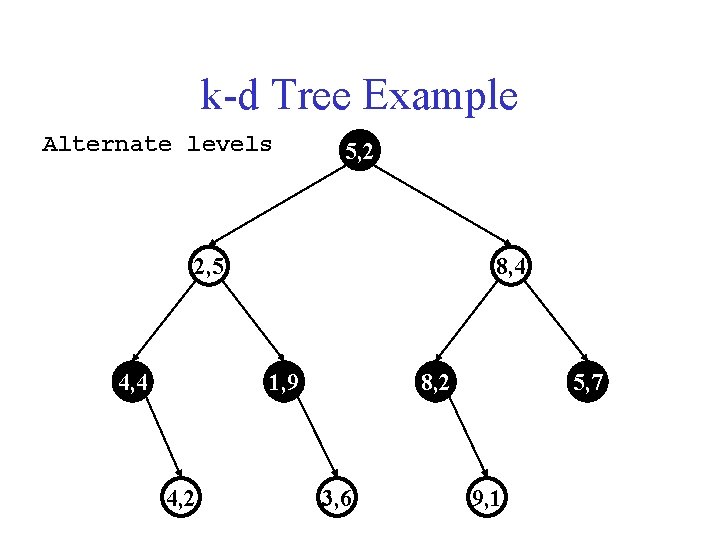
k-d Tree Example Alternate levels 5, 2 2, 5 4, 4 8, 4 1, 9 4, 2 8, 2 3, 6 5, 7 9, 1

Find in a k-d Tree find(<x 1, x 2, …, xk>, root) Alternate levels Runtime? [O (depth) ]

k-d Trees can be unbalanced insert(<5, 0>) insert(<6, 9>) insert(<9, 3>) insert(<6, 5>) insert(<7, 7>) insert(<8, 6>) 5, 0 6, 9 9, 3 6, 5 7, 7 8, 6

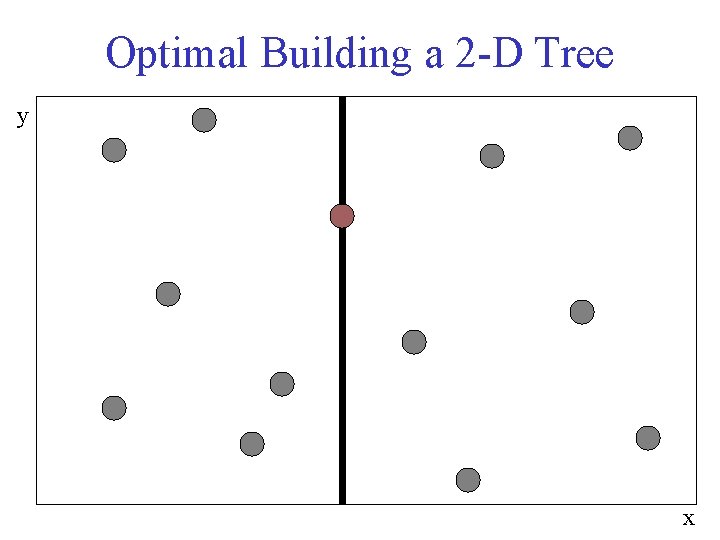
Height of k-d Trees • 1. Could be unbalanced • 2. Random: – O(log N) average – O(N) worst case • 3. If building in batch, choose the median along the current dimension at each level – guarantees O(log. N) height – Total cost O(Nlog. N) to build

Optimal Building a 2 -D Tree y x

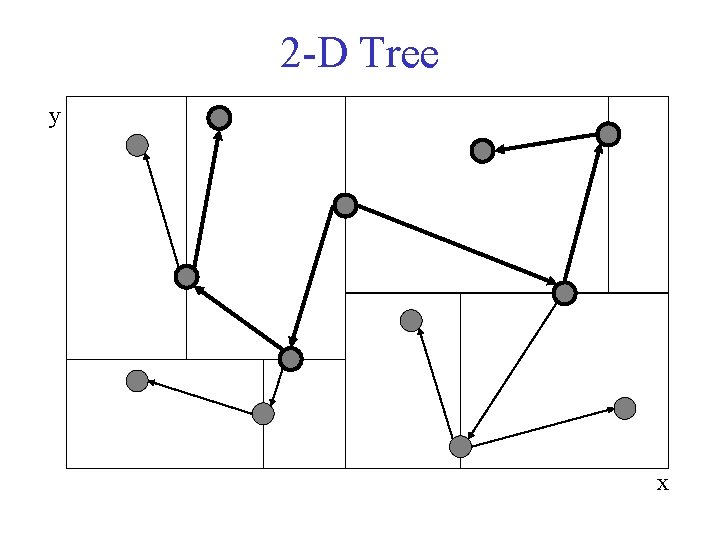
2 -D Tree y x

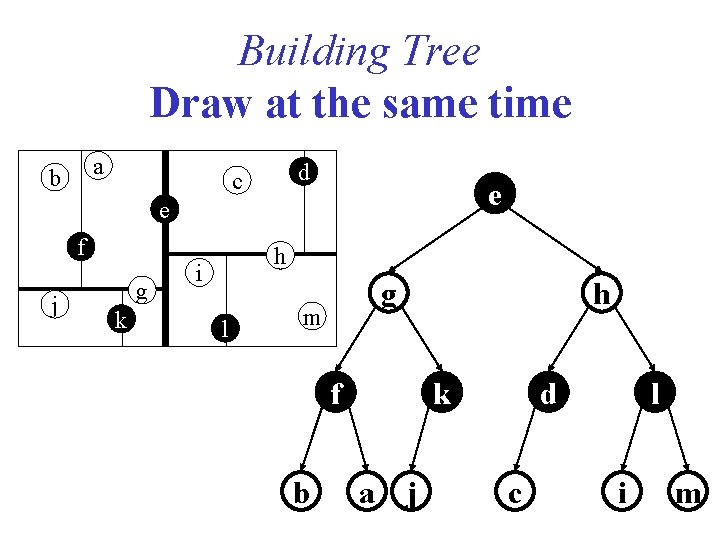
Building Tree Draw at the same time a b d c e e f j g k h i l g m f b h k a j d c l i m

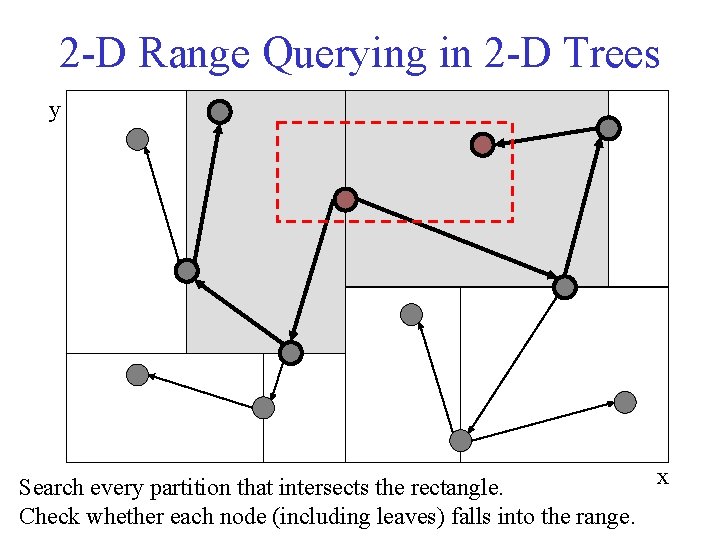
2 -D Range Querying in 2 -D Trees y x Search every partition that intersects the rectangle. Check whether each node (including leaves) falls into the range.

2 -D Range Querying in 2 -D Trees • Runtime: – Depends on balance and # of matches – Perfect balance: O(M + sqrt(N)) worst (M = number of matches) (for 1 -D BST, = O(M + log. N) average

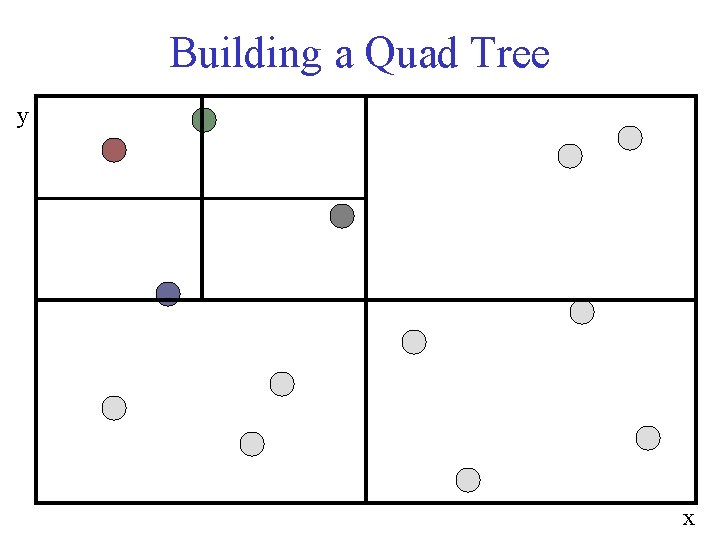
Quad Trees • Split on all (two) dimensions at each level • Split key space into equal size partitions (quadrants) • Add a new node by adding to a leaf, and, if the leaf is already occupied, split until only one node per leaf

Building a Quad Tree y x

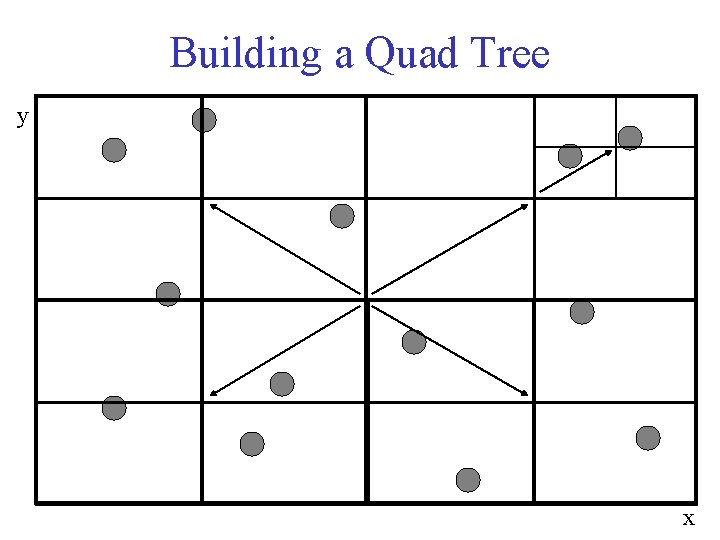
Building a Quad Tree y x

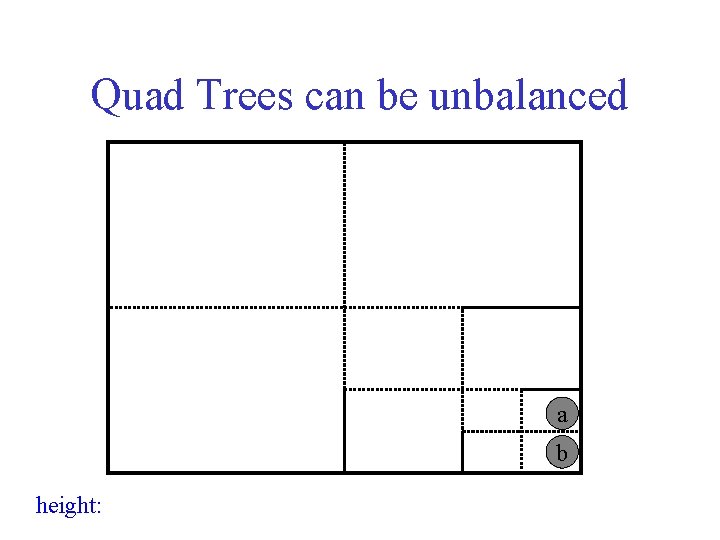
Quad Trees can be unbalanced a b height:

Height of Quad Tree • Height of the tree is O(log n + log ) – is the ratio of the width (or height) of the key space and the smallest distance between two points • Supports insert, delete, find, nearest neighbor, range queries

Quad Trees vs. k-D Trees • k-D Trees – – Density balanced trees Number of nodes is O(n) where n is the number of points Height of the tree is O(log n) with batch insertion Supports insert, find, nearest neighbor, range queries • Quad Trees – Number of nodes is O(n(1+ log( /n))) where n is the number of points and is the ratio of the width (or height) of the key space and the smallest distance between two points – Height of the tree is O(log n + log ) – Supports insert, delete, find, nearest neighbor, range queries