CSE 326 Data Structures Splay Trees Ben Lerner

CSE 326: Data Structures Splay Trees Ben Lerner Summer 2007

Administrivia • Midterm July 16 during lecture – Topics posted, Review next week • Project 2 c posted early next week 2

Self adjustment for better living • Ordinary binary search trees have no balance conditions – what you get from insertion order is it • Balanced trees like AVL trees enforce a balance condition when nodes change – tree is always balanced after an insert or delete • Self-adjusting trees get reorganized over time as nodes are accessed 3

Splay Trees • Blind adjusting version of AVL trees – Why worry about balances? Just rotate anyway! • Amortized time per operations is O(log n) • Worst case time per operation is O(n) – But guaranteed to happen rarely Insert/Find always rotate node to the root! 4

Amortized Complexity If a sequence of M operations takes O(M f(n)) time, we say the amortized runtime is O(f(n)). • Worst case time per operation can still be large, say O(n) • Worst case time for any sequence of M operations is O(M f(n)) Average time per operation for any sequence is O(f(n)) Amortized complexity is worst-case guarantee over sequences of operations. 5

Amortized Complexity • Is amortized guarantee any weaker than worstcase? • Is amortized guarantee any stronger than averagecase? • Is average case guarantee good enough in practice? • Is amortized guarantee good enough in practice? 6

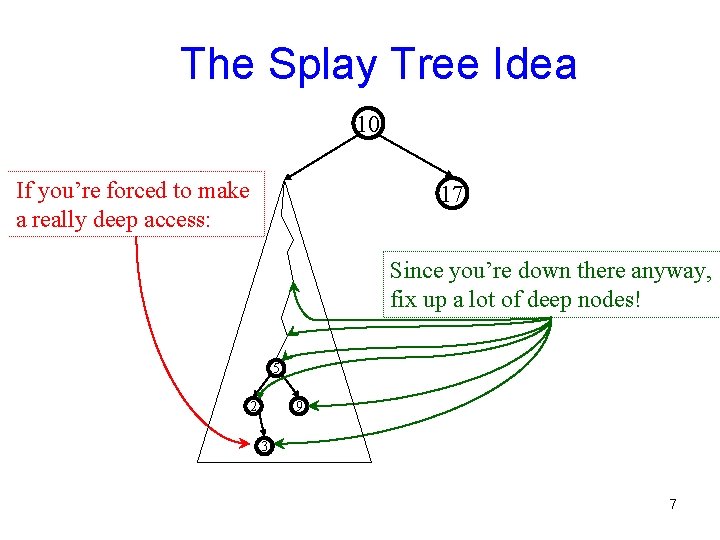
The Splay Tree Idea 10 If you’re forced to make a really deep access: 17 Since you’re down there anyway, fix up a lot of deep nodes! 5 2 9 3 7

Find/Insert in Splay Trees 1. Find or insert a node k 2. Splay k to the root using: zig-zag, zig-zig, or plain old zig rotation Why could this be good? ? 1. Helps the new root, k o Great if k is accessed again 2. And helps many others! o Great if many others on the path are accessed 8

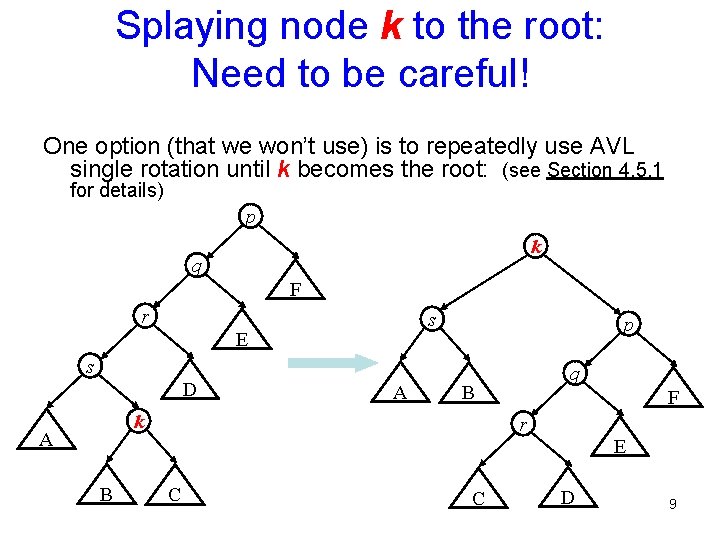
Splaying node k to the root: Need to be careful! One option (that we won’t use) is to repeatedly use AVL single rotation until k becomes the root: (see Section 4. 5. 1 for details) p k q F r s E p s D A B k A q F r E B C C D 9

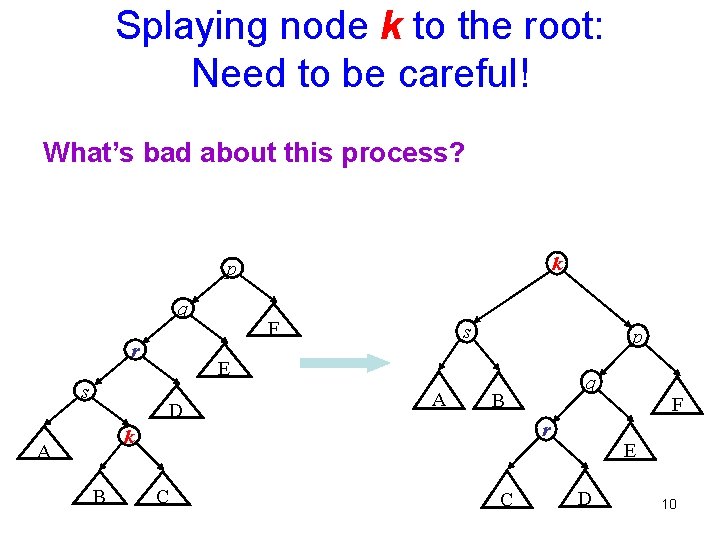
Splaying node k to the root: Need to be careful! What’s bad about this process? k p q r s F s p E D A B B C F r k A q C E D 10

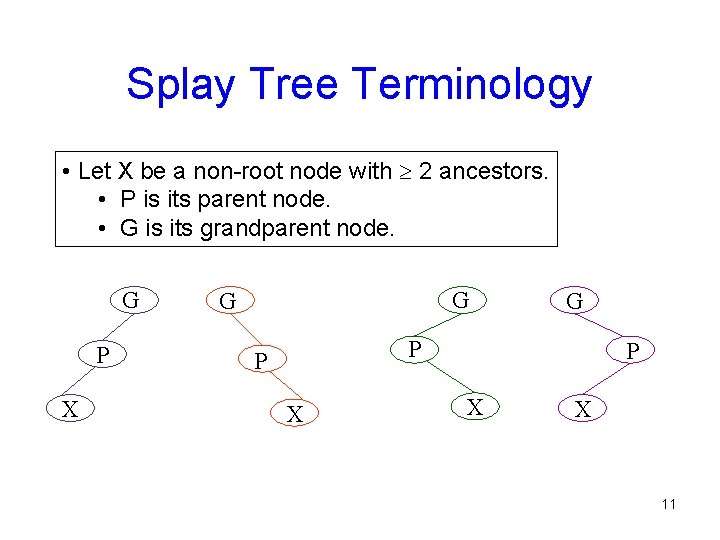
Splay Tree Terminology • Let X be a non-root node with 2 ancestors. • P is its parent node. • G is its grandparent node. G P X G G G P P X X 11

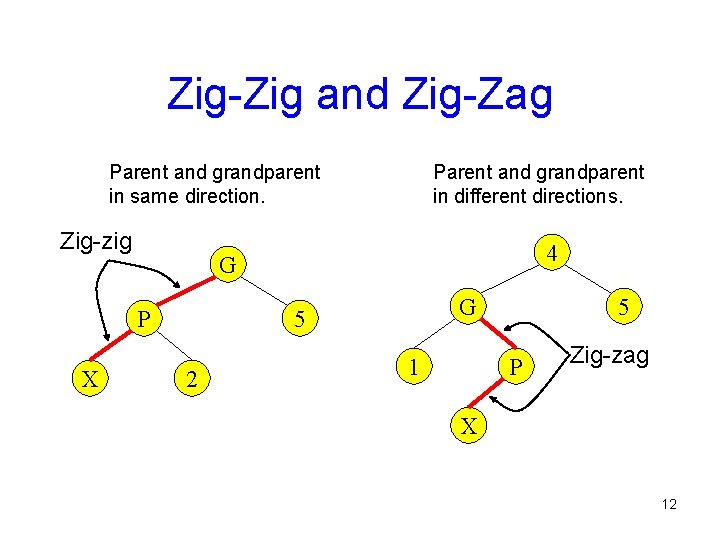
Zig-Zig and Zig-Zag Parent and grandparent in same direction. Zig-zig 4 G P X Parent and grandparent in different directions. G 5 2 1 5 P Zig-zag X 12

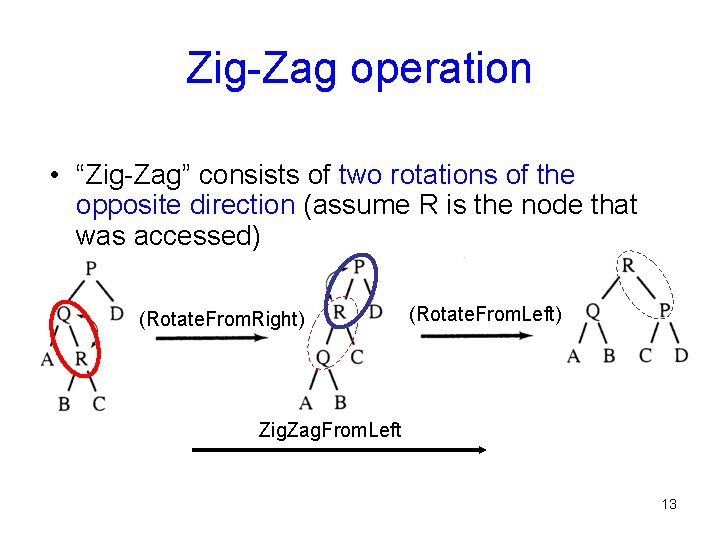
Zig-Zag operation • “Zig-Zag” consists of two rotations of the opposite direction (assume R is the node that was accessed) (Rotate. From. Right) (Rotate. From. Left) Zig. Zag. From. Left 13

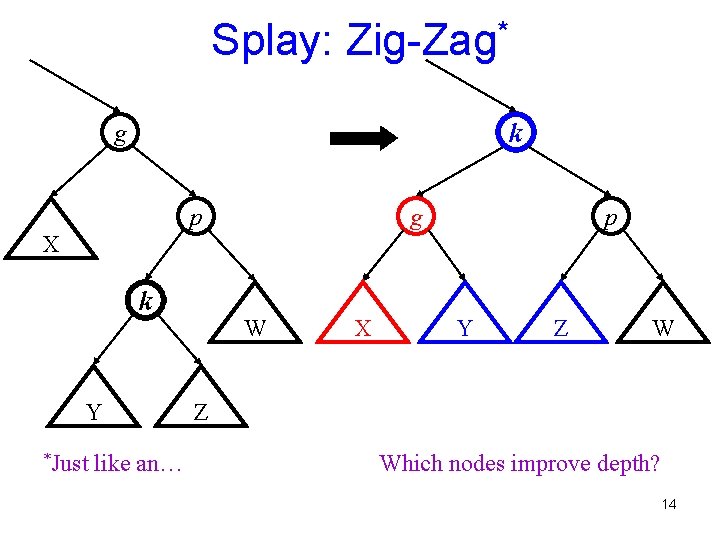
Splay: Zig-Zag* k g p X k Y *Just like an… W X Y Z Which nodes improve depth? 14

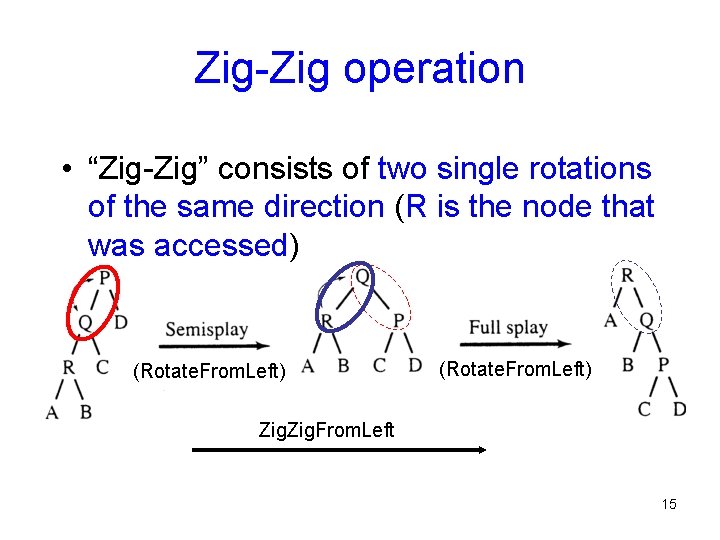
Zig-Zig operation • “Zig-Zig” consists of two single rotations of the same direction (R is the node that was accessed) (Rotate. From. Left) Zig. From. Left 15

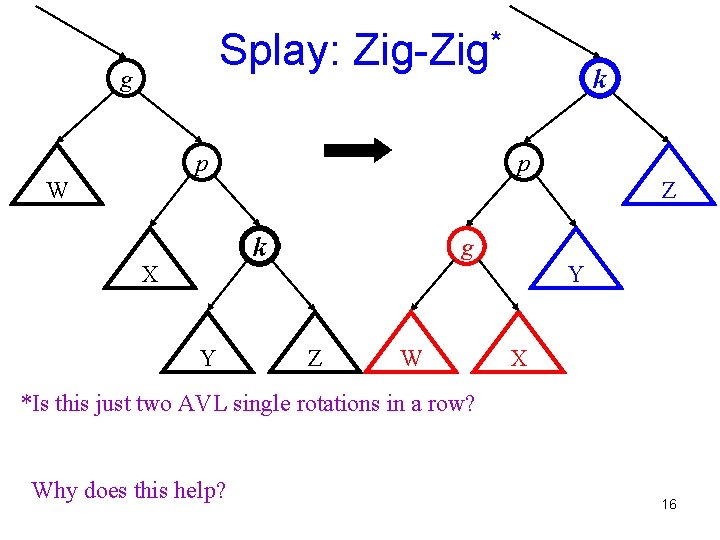
Splay: g * Zig-Zig p k p W Z k X Y g Y Z W X *Is this just two AVL single rotations in a row? Why does this help? 16

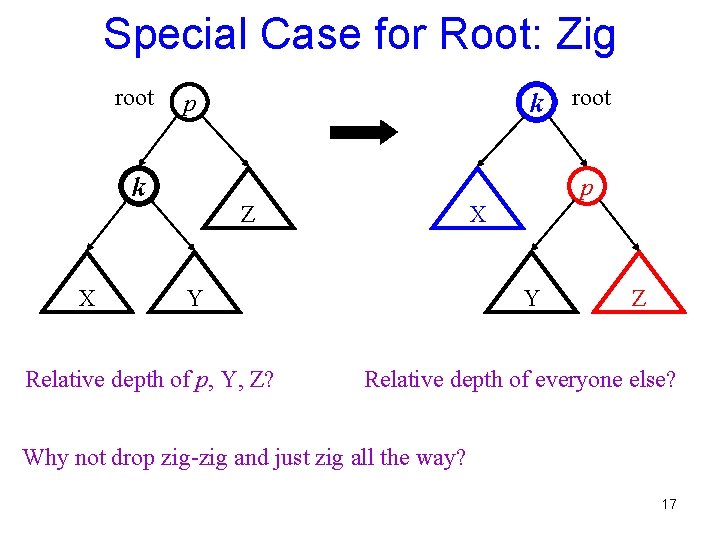
Special Case for Root: Zig root k X k p root p Z X Y Relative depth of p, Y, Z? Y Z Relative depth of everyone else? Why not drop zig-zig and just zig all the way? 17

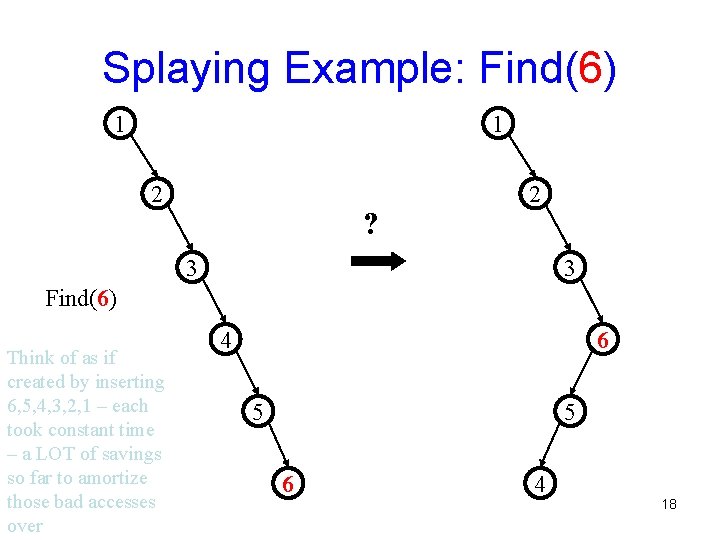
Splaying Example: Find(6) 1 1 2 ? 2 3 3 Find(6) Think of as if created by inserting 6, 5, 4, 3, 2, 1 – each took constant time – a LOT of savings so far to amortize those bad accesses over 4 6 5 5 6 4 18

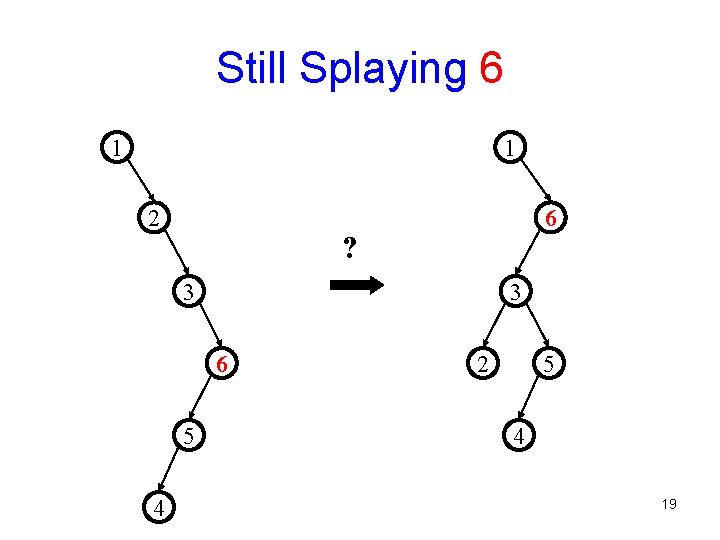
Still Splaying 6 1 1 2 6 ? 3 3 6 5 4 2 5 4 19

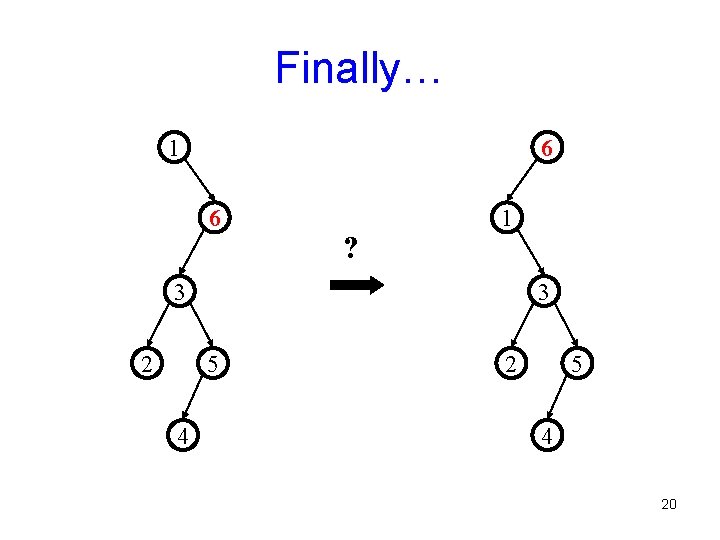
Finally… 1 6 6 ? 1 3 2 3 5 4 20

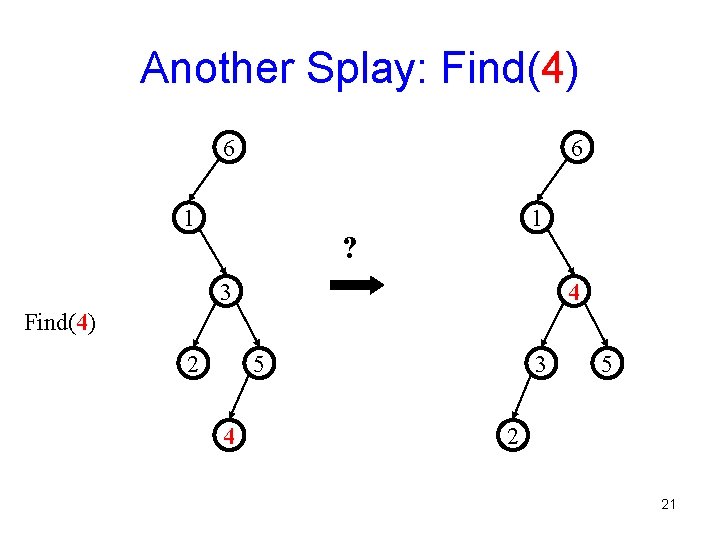
Another Splay: Find(4) 6 6 1 1 ? 3 4 Find(4) 2 5 4 3 5 2 21

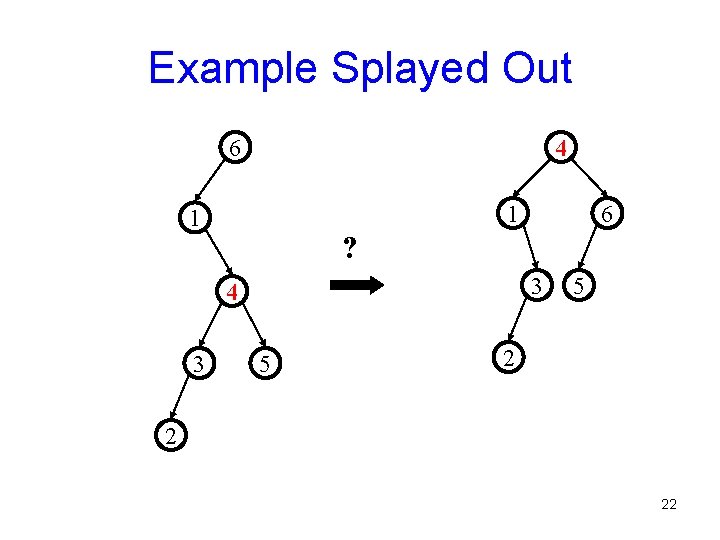
Example Splayed Out 6 4 1 1 ? 3 4 3 6 5 5 2 2 22

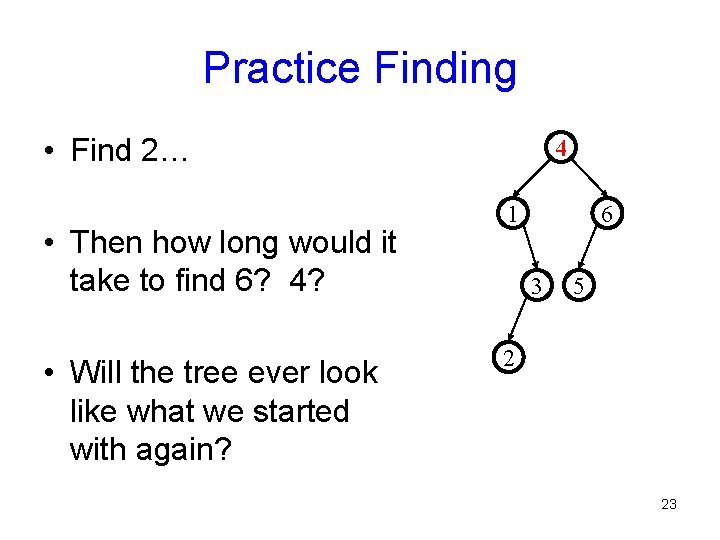
Practice Finding • Find 2… • Then how long would it take to find 6? 4? • Will the tree ever look like what we started with again? 4 1 6 3 5 2 23

But Wait… What happened here? Didn’t two find operations take linear time instead of logarithmic? What about the amortized O(log n) guarantee? 24

Why Splaying Helps • If a node n on the access path is at depth d before the splay, it’s at about depth d/2 after the splay • Overall, nodes which are low on the access path tend to move closer to the root • Splaying gets amortized O(log n) performance. (Maybe not now, but soon, and for the rest of the operations. ) 25

Practical Benefit of Splaying • No heights to maintain, no imbalance to check for – Less storage per node, easier to code • Often data that is accessed once, is soon accessed again! – Splaying does implicit caching by bringing it to the root 26

Splay Operations: Find • Find the node in normal BST manner • Splay the node to the root – if node not found, splay what would have been its parent What if we didn’t splay? 27

Splay Operations: Insert • Insert the node in normal BST manner • Splay the node to the root What if we didn’t splay? 28

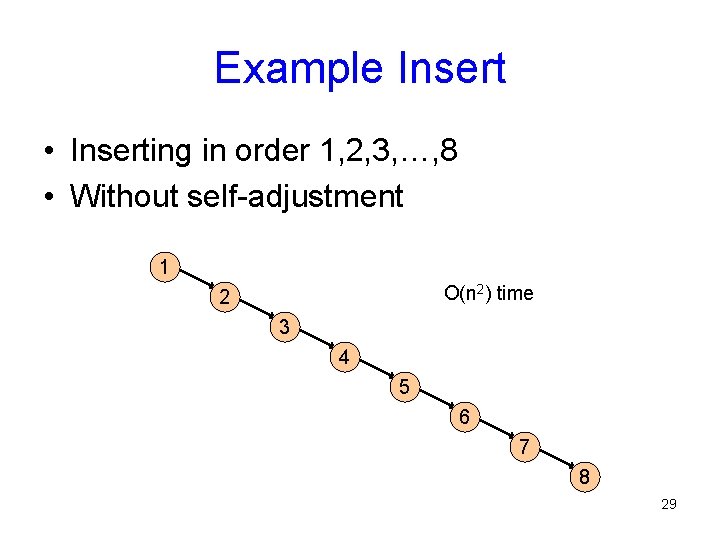
Example Insert • Inserting in order 1, 2, 3, …, 8 • Without self-adjustment 1 O(n 2) time 2 3 4 5 6 7 8 29

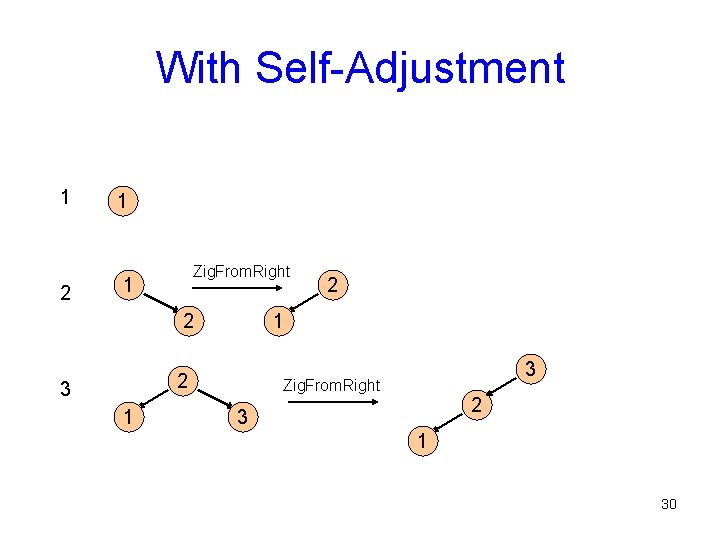
With Self-Adjustment 1 2 1 Zig. From. Right 1 2 3 Zig. From. Right 2 3 1 30

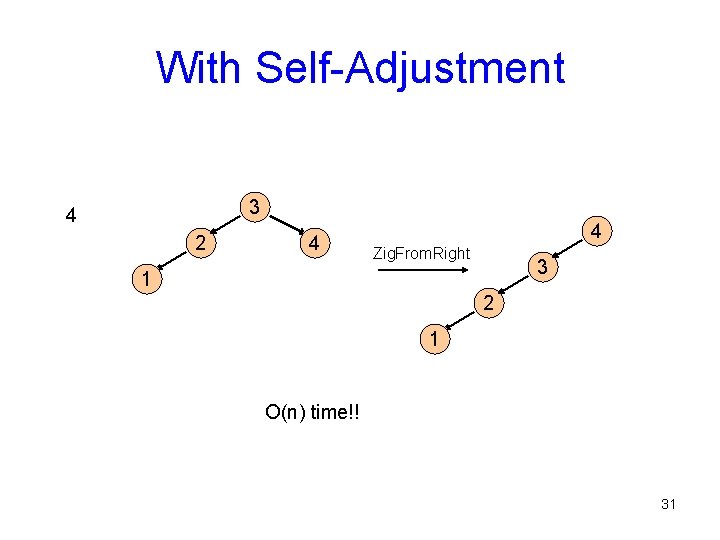
With Self-Adjustment 3 4 2 4 4 Zig. From. Right 3 1 2 1 O(n) time!! 31

Splay Operations: Remove k find(k) delete k L R L <k R >k Now what? 32

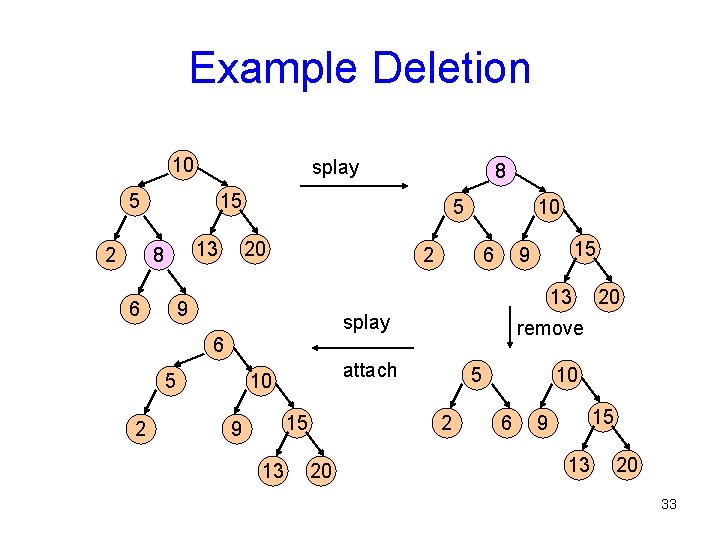
Example Deletion 10 splay 5 2 8 15 13 8 6 5 20 10 2 6 13 9 splay 5 attach 10 15 9 13 5 2 20 20 remove 6 2 15 9 10 6 15 9 13 20 33

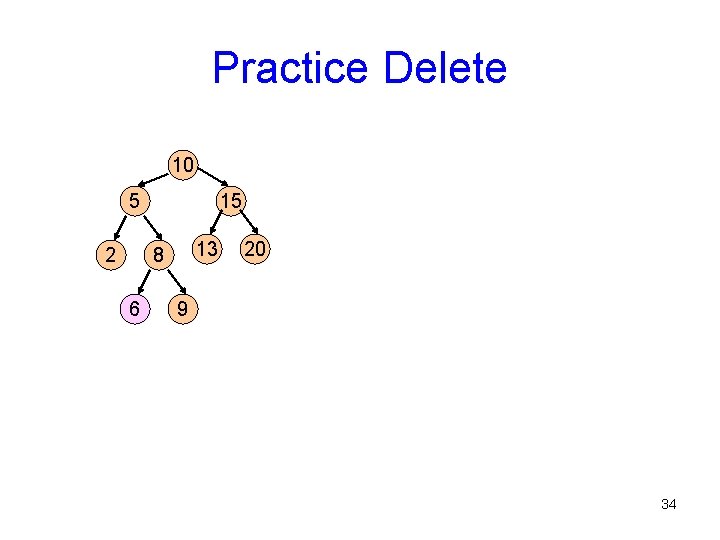
Practice Delete 10 5 2 15 13 8 6 20 9 34

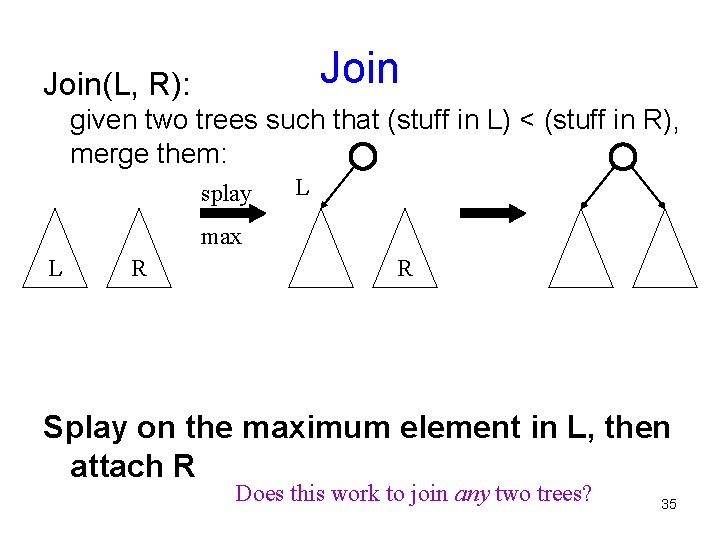
Join(L, R): given two trees such that (stuff in L) < (stuff in R), merge them: splay L max L R R Splay on the maximum element in L, then attach R Does this work to join any two trees? 35

Splay Tree Summary • All operations are in amortized O(log n) time • Splaying can be done top-down; this may be better because: – only one pass – no recursion or parent pointers necessary – we didn’t cover top-down in class • Splay trees are very effective search trees – Relatively simple – No extra fields required – Excellent locality properties: frequently accessed keys are cheap to find 36