CSE 326 Data Structures Lecture 17 Priority Queues

CSE 326: Data Structures Lecture #17 Priority Queues Alon Halevy Spring Quarter 2001

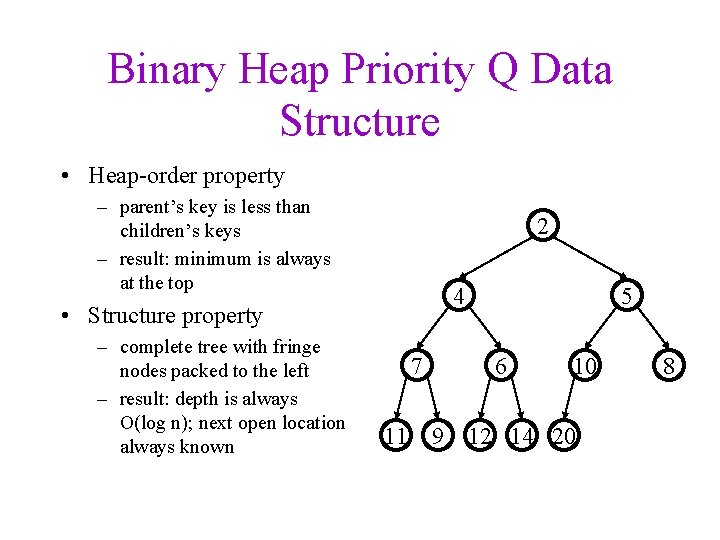
Binary Heap Priority Q Data Structure • Heap-order property – parent’s key is less than children’s keys – result: minimum is always at the top 2 4 • Structure property – complete tree with fringe nodes packed to the left – result: depth is always O(log n); next open location always known 7 11 9 5 6 10 12 14 20 8

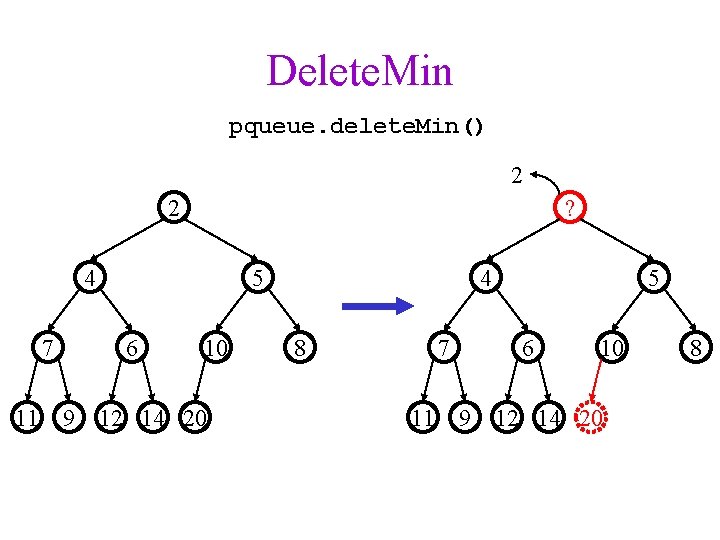
Delete. Min pqueue. delete. Min() 2 2 ? 4 7 11 5 6 10 9 12 14 20 4 8 7 11 9 5 6 10 12 14 20 8

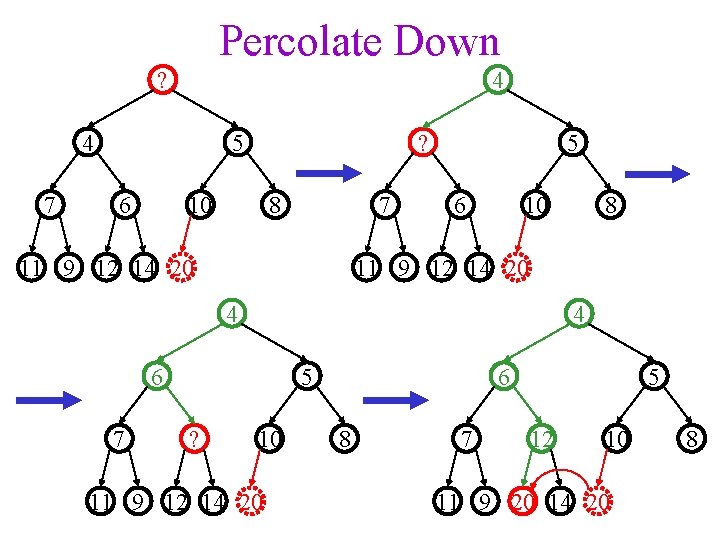
Percolate Down ? 4 4 7 5 6 ? 10 8 7 11 9 12 14 20 5 6 10 11 9 12 14 20 4 4 6 7 5 ? 8 10 11 9 12 14 20 6 8 7 5 12 10 11 9 20 14 20 8

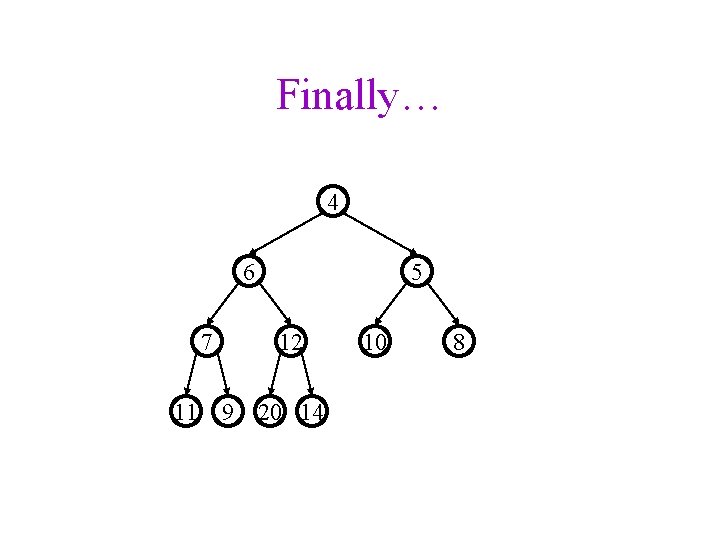
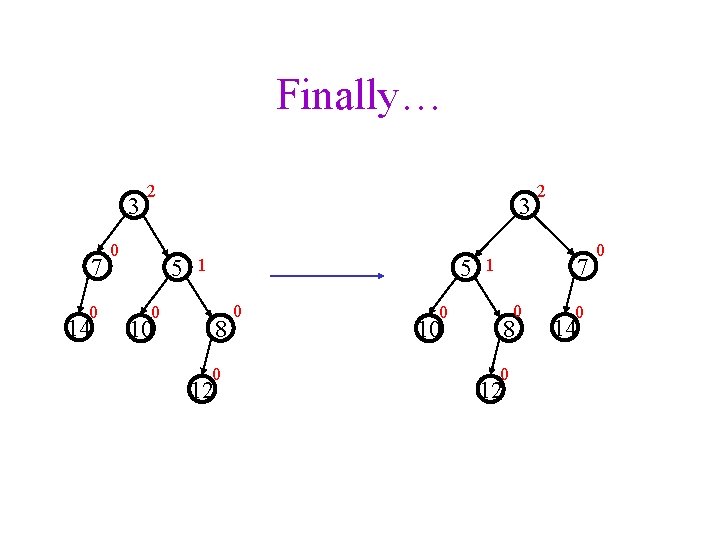
Finally… 4 6 5 7 12 11 9 20 14 10 8

Delete. Min Code Object delete. Min() { assert(!is. Empty()); return. Val = Heap[1]; size--; new. Pos = percolate. Down(1, Heap[size+1]); Heap[new. Pos] = Heap[size + 1]; return. Val; } int percolate. Down(int hole, Object val) { while (2*hole <= size) { left = 2*hole; right = left + 1; if (right <= size && Heap[right] < Heap[left]) target = right; else target = left; if (Heap[target] < val) { Heap[hole] = Heap[target]; hole = target; } else break; runtime: } return hole; }

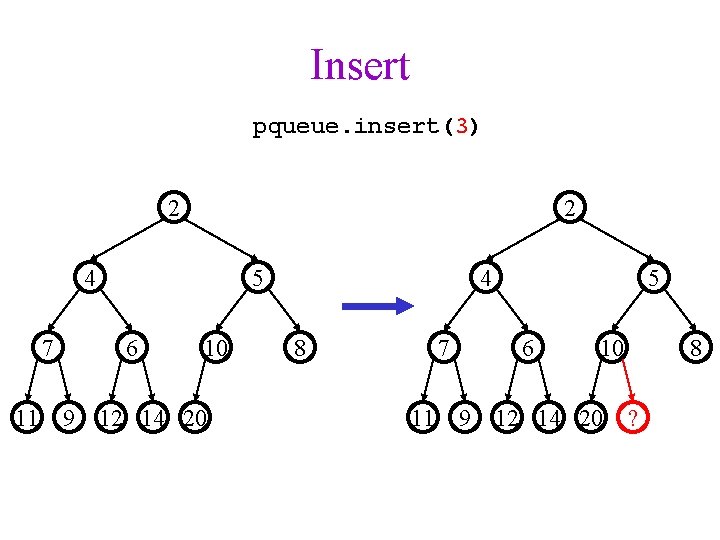
Insert pqueue. insert(3) 2 2 4 7 11 5 6 10 9 12 14 20 4 8 7 11 9 5 6 10 12 14 20 8 ?

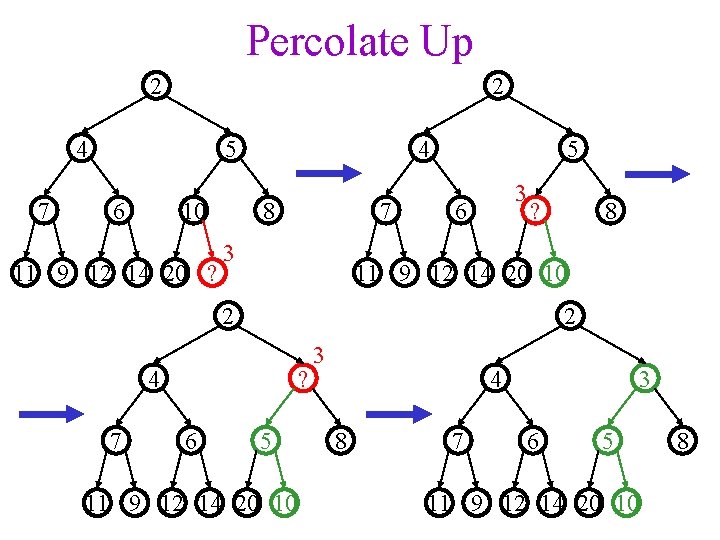
Percolate Up 2 2 4 7 5 6 10 11 9 12 14 20 ? 4 8 7 3 5 3 6 ? 11 9 12 14 20 10 2 2 4 7 ? 6 8 5 11 9 12 14 20 10 3 4 8 7 3 6 5 11 9 12 14 20 10 8

Insert Code void insert(Object o) { assert(!is. Full()); size++; new. Pos = percolate. Up(size, o); Heap[new. Pos] = o; } runtime: int percolate. Up(int hole, Object val) { while (hole > 1 && val < Heap[hole/2]) Heap[hole] = Heap[hole/2]; hole /= 2; } return hole; }

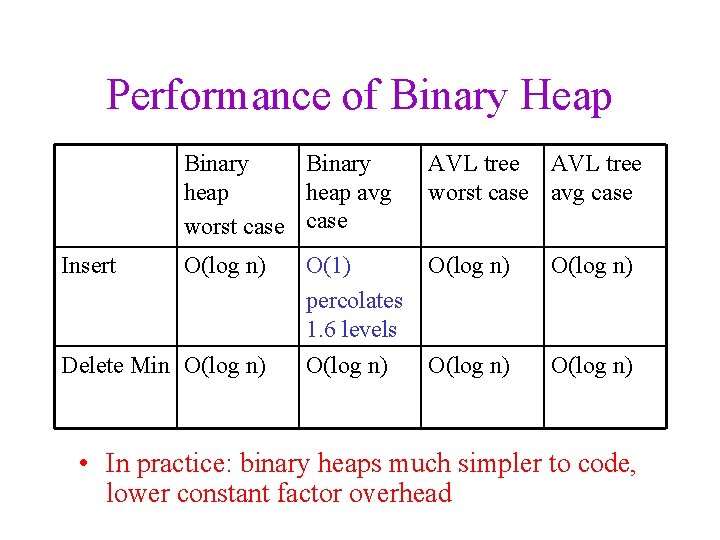
Performance of Binary Heap Insert Binary heap avg worst case AVL tree worst case avg case O(log n) O(1) percolates 1. 6 levels O(log n) O(log n) Delete Min O(log n) • In practice: binary heaps much simpler to code, lower constant factor overhead

Changing Priorities • In many applications the priority of an object in a priority queue may change over time – if a job has been sitting in the printer queue for a long time increase its priority – unix “renice” – Alon’s story • Must have some (separate) way of find the position in the queue of the object to change (e. g. a hash table)

Other Priority Queue Operations • decrease. Key – given the position of an object in the queue, reduce its priority value • increase. Key – given the position of an an object in the queue, increase its priority value • remove – given the position of an object in the queue, remove it • build. Heap – given a set of items, build a heap

Decrease. Key, Increase. Key, and Remove void decrease. Key(int pos, int delta){ temp = Heap[pos] - delta; new. Pos = percolate. Up(pos, temp); Heap[new. Pos] = temp; } void increase. Key(int pos, int delta) { temp = Heap[pos] + delta; new. Pos = percolate. Down(pos, temp); Heap[new. Pos] = temp; } void remove(int pos) { percolate. Up(pos, NEG_INF_VAL); delete. Min(); }

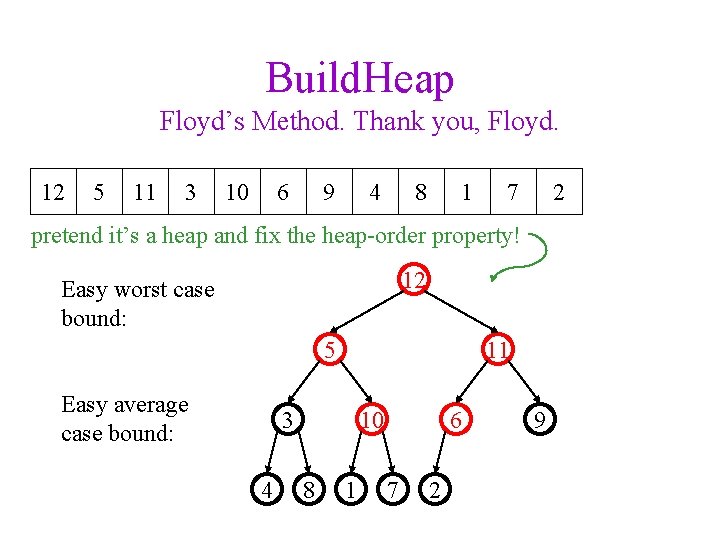
Build. Heap Floyd’s Method. Thank you, Floyd. 12 5 11 3 10 6 9 4 8 1 7 2 pretend it’s a heap and fix the heap-order property! 12 Easy worst case bound: 5 Easy average case bound: 11 3 4 10 8 1 6 7 2 9

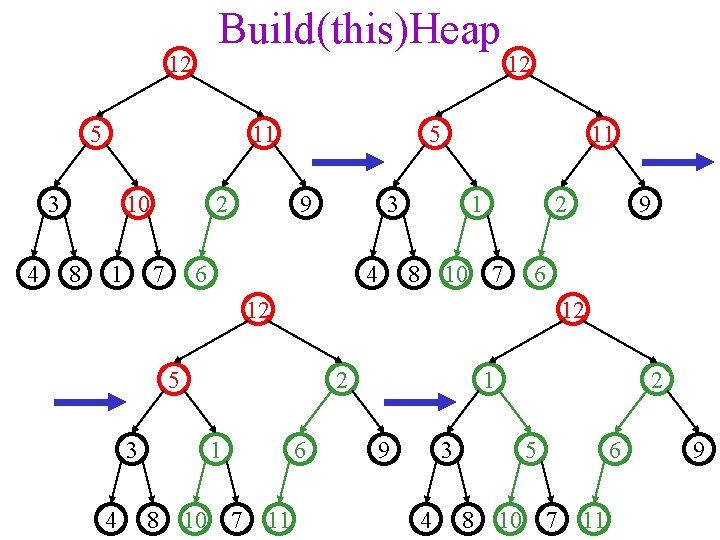
Build(this)Heap 12 5 11 3 4 10 8 1 2 7 12 5 9 11 3 6 4 1 8 2 10 7 6 12 12 5 3 4 2 1 8 10 7 6 11 9 3 4 2 5 8 10 7 6 11 9

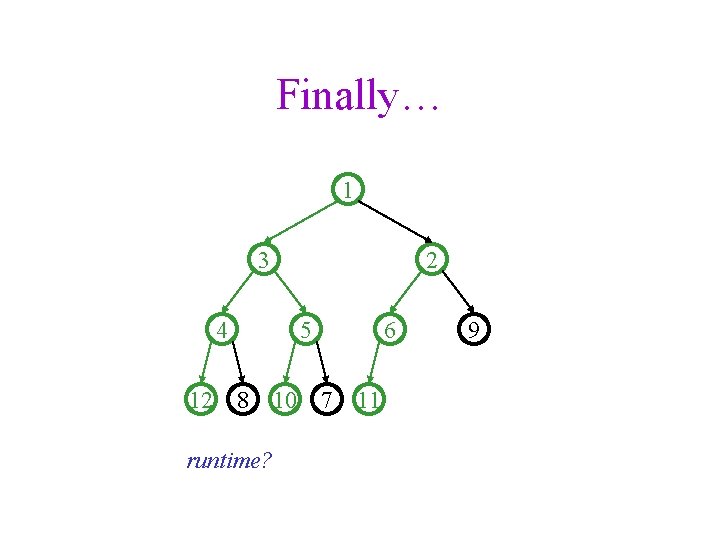
Finally… 1 3 2 4 5 12 8 10 7 runtime? 6 11 9

Complexity of Build Heap • Note: size of a perfect binary tree doubles (+1) with each additional layer • At most n/4 percolate down 1 level at most n/8 percolate down 2 levels at most n/16 percolate down 3 levels… O(n)

Thinking about Heaps • Observations – – finding a child/parent index is a multiply/divide by two operations jump widely through the heap each operation looks at only two new nodes inserts are at least as common as delete. Mins • Realities – division and multiplication by powers of two are fast – looking at one new piece of data terrible in a cache line – with huge data sets, disk accesses dominate

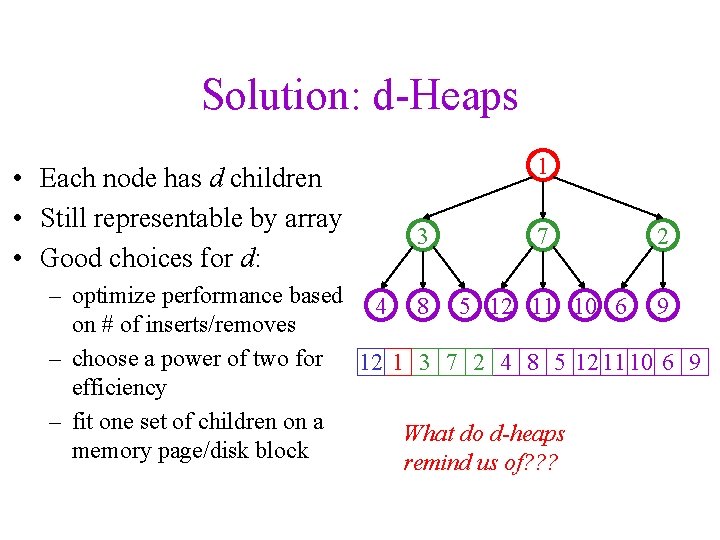
Solution: d-Heaps • Each node has d children • Still representable by array • Good choices for d: 1 3 7 2 – optimize performance based 4 8 5 12 11 10 6 9 on # of inserts/removes – choose a power of two for 12 1 3 7 2 4 8 5 12 11 10 6 9 efficiency – fit one set of children on a What do d-heaps memory page/disk block remind us of? ? ?

New Operation: Merge Given two heaps, merge them into one heap – first attempt: insert each element of the smaller heap into the larger. runtime: – second attempt: concatenate heaps’ arrays and run build. Heap. runtime: How about O(log n) time?

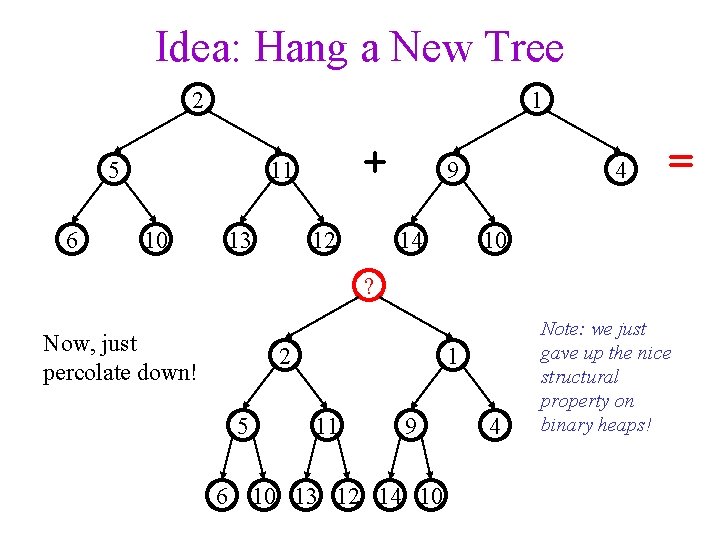
Idea: Hang a New Tree 2 1 5 6 + 11 10 13 12 9 14 4 = 10 ? Now, just percolate down! 2 5 6 1 11 9 10 13 12 14 10 4 Note: we just gave up the nice structural property on binary heaps!

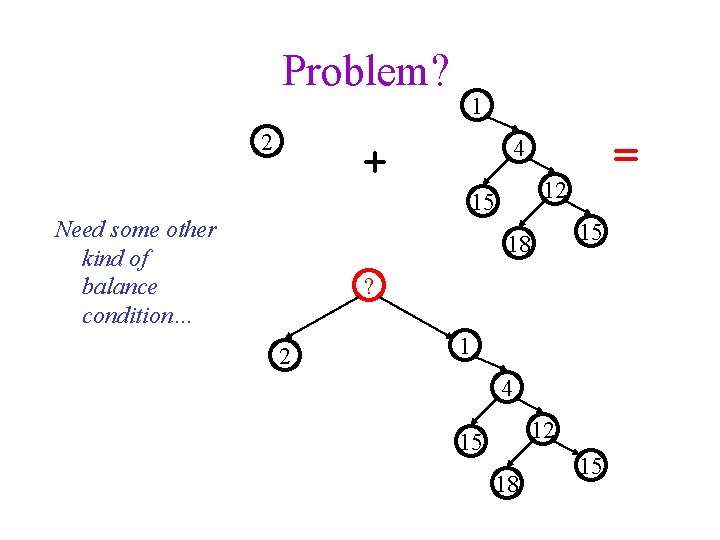
Problem? 2 1 + 12 15 Need some other kind of balance condition… = 4 15 18 ? 2 1 4 12 15 18 15

Leftist Heaps • Idea: make it so that all the work you have to do in maintaining a heap is in one small part • Leftist heap: – almost all nodes are on the left – all the merging work is on the right

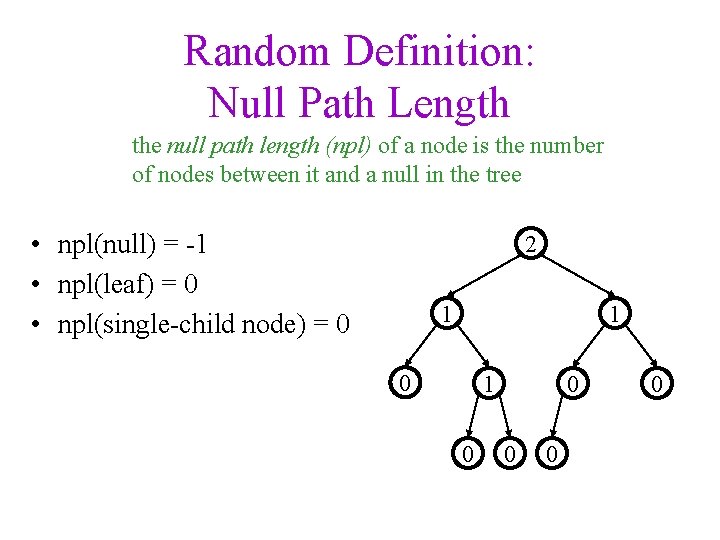
Random Definition: Null Path Length the null path length (npl) of a node is the number of nodes between it and a null in the tree • npl(null) = -1 • npl(leaf) = 0 • npl(single-child node) = 0 2 1 1 0 0 0

Leftist Heap Properties • Heap-order property – parent’s priority value is to childrens’ priority values – result: minimum element is at the root • Leftist property – null path length of left subtree is npl of right subtree – result: tree is at least as “heavy” on the left as the right Are leftist trees complete? Balanced?

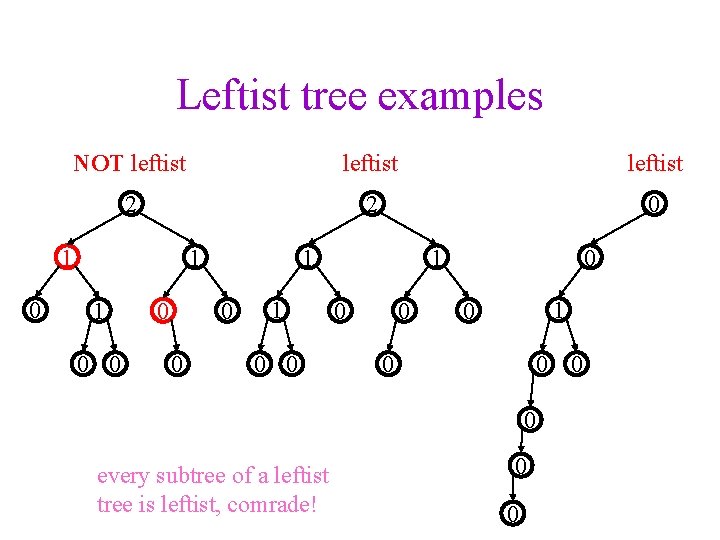
Leftist tree examples NOT leftist 2 2 0 1 1 0 0 0 1 0 0 0 every subtree of a leftist tree is leftist, comrade! 0 0

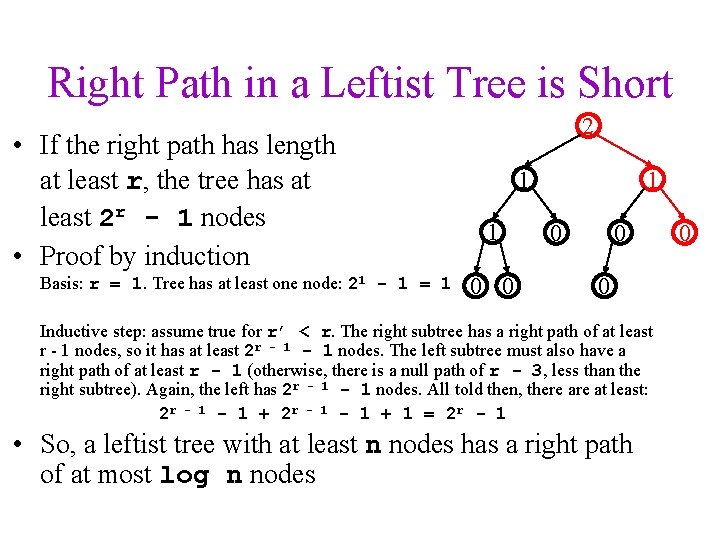
Right Path in a Leftist Tree is Short • If the right path has length at least r, the tree has at least 2 r - 1 nodes • Proof by induction Basis: r = 1. Tree has at least one node: 21 - 1 = 1 2 1 1 0 0 0 Inductive step: assume true for r’ < r. The right subtree has a right path of at least r - 1 nodes, so it has at least 2 r - 1 nodes. The left subtree must also have a right path of at least r - 1 (otherwise, there is a null path of r - 3, less than the right subtree). Again, the left has 2 r - 1 nodes. All told then, there at least: 2 r - 1 + 2 r - 1 + 1 = 2 r - 1 • So, a leftist tree with at least n nodes has a right path of at most log n nodes 0

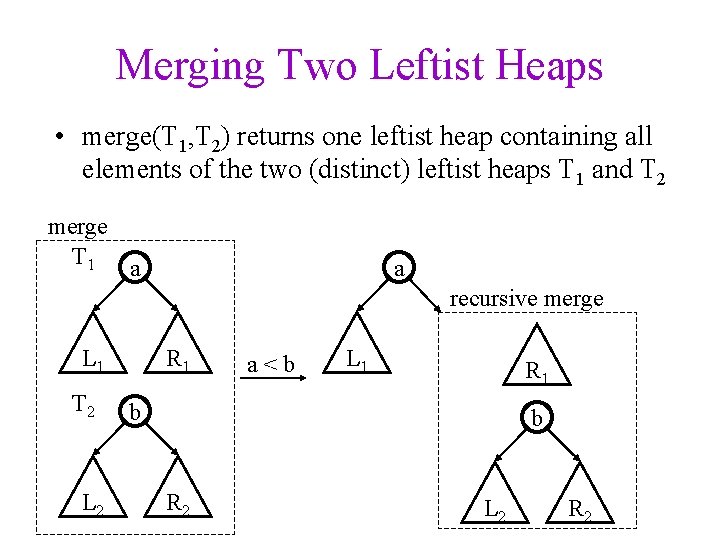
Merging Two Leftist Heaps • merge(T 1, T 2) returns one leftist heap containing all elements of the two (distinct) leftist heaps T 1 and T 2 merge T 1 a a recursive merge L 1 T 2 L 2 R 1 a<b L 1 R 1 b b R 2 L 2 R 2

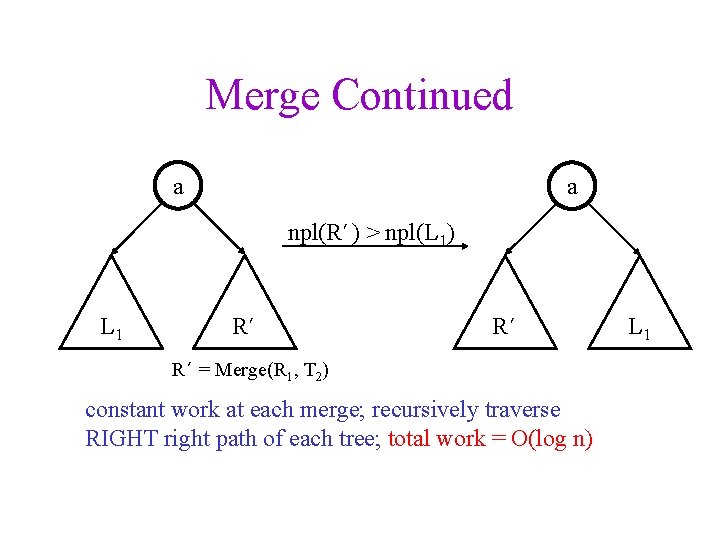
Merge Continued a a npl(R’) > npl(L 1) L 1 R’ R’ R’ = Merge(R 1, T 2) constant work at each merge; recursively traverse RIGHT right path of each tree; total work = O(log n) L 1

Operations on Leftist Heaps • merge with two trees of total size n: O(log n) • insert with heap size n: O(log n) – pretend node is a size 1 leftist heap – insert by merging original heap with one node heap merge • delete. Min with heap size n: O(log n) – remove and return root – merge left and right subtrees merge

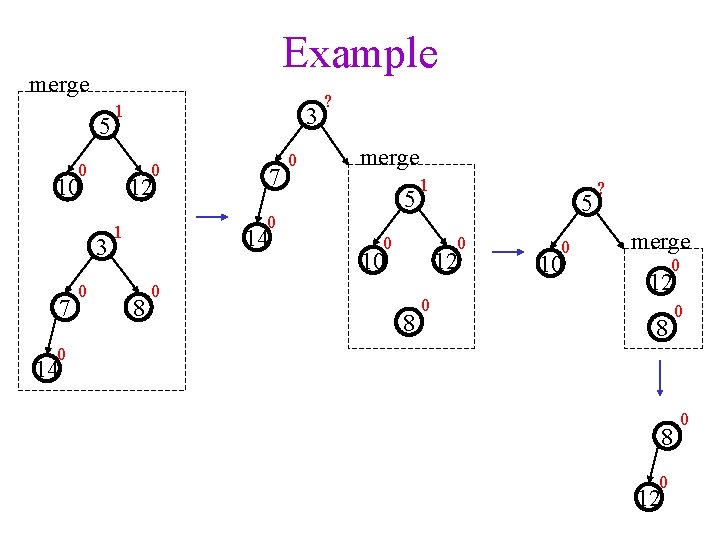
Example merge 5 1 0 0 10 7 7 12 3 0 ? merge 5 0 1 14 8 1 0 5 0 10 12 0 8 0 0 10 ? merge 0 12 8 0 0 14 8 0 12 0

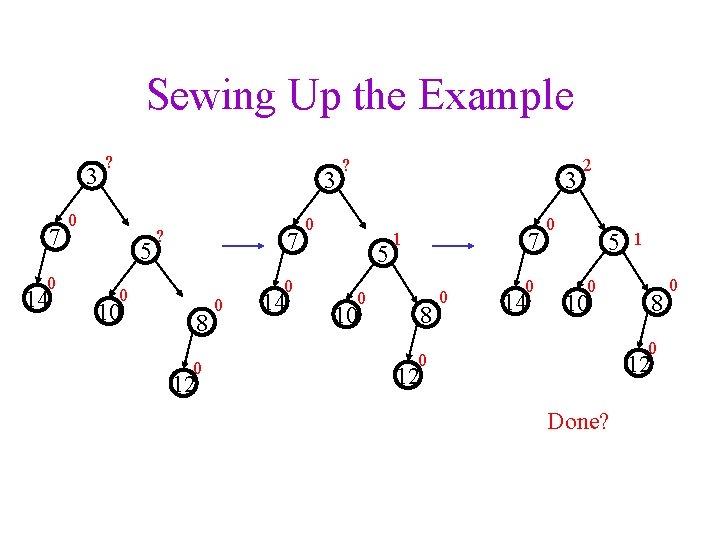
Sewing Up the Example 3 7 0 14 ? 3 0 5 ? 7 0 10 8 0 12 0 0 14 ? 3 0 5 7 1 0 8 10 0 0 14 2 0 5 1 0 8 10 0 12 Done? 0

Finally… 3 7 0 14 2 0 3 5 5 1 0 8 10 0 12 0 2 7 1 0 0 8 10 0 12 0 14 0

Skew Heaps • Problems with leftist heaps – extra storage for npl – two pass merge (with stack!) – extra complexity/logic to maintain and check npl • Solution: skew heaps – – – blind adjusting version of leftist heaps amortized time for merge, insert, and delete. Min is O(log n) worst case time for all three is O(n) merge always switches children when fixing right path iterative method has only one pass What do skew heaps remind us of?

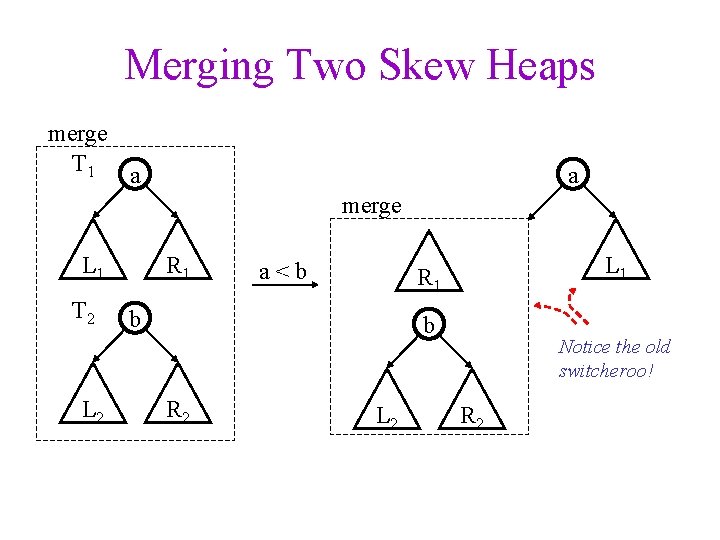
Merging Two Skew Heaps merge T 1 a a merge L 1 T 2 L 2 R 1 a<b L 1 R 1 b b R 2 L 2 Notice the old switcheroo! R 2

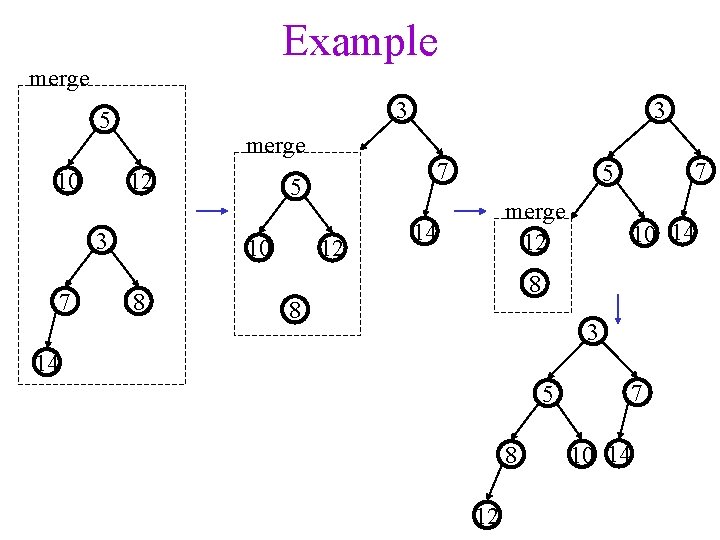
Example merge 3 5 10 merge 12 3 7 3 5 10 8 7 12 7 5 merge 12 14 10 14 8 8 3 14 7 5 8 12 10 14

Skew Heap Code void merge(heap 1, heap 2) { case { heap 1 == NULL: return heap 2; heap 2 == NULL: return heap 1; heap 1. find. Min() < heap 2. find. Min(): temp = heap 1. right; heap 1. right = heap 1. left; heap 1. left = merge(heap 2, temp); return heap 1; otherwise: return merge(heap 2, heap 1); } }

Comparing Heaps • Binary Heaps • Leftist Heaps • d-Heaps • Skew Heaps • Binomial Queues