CSE 324 Operations Research and Management Systems Lec

CSE 324: Operations Research and Management Systems Lec 09 Transportation, Assignment, Transshipment Problems (1) Dr. Ahmed Mahmoud

What are “Those” Problems? • Special types of LP. • Transportation problem: Optimal transportation and allocation of resources. • Assignment problem: Optimal assignment of agents to tasks. • Transshipment problem: Subcategory of transport problem where it must go through intermediate nodes, possibly changing modes of transport. • These problems can be solved by simplex (as an LP). • Simplex is inefficient. • Specialized algorithms for each problem are available and more efficient. 18/4/2019 CSE 324 OR: Lec 09 2

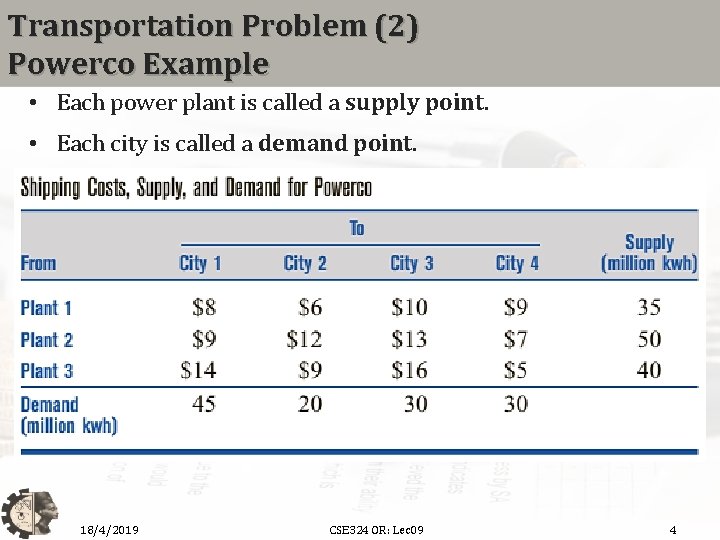
Transportation Problem (1) Powerco Example • Powerco has three electric power plants that supply the needs of four cities. • Each power plant can supply the following numbers of kilowatthours (kwh) of electricity: plant 1— 35 million; plant 2— 50 million; plant 3— 40 million. • The peak power demands in these cities, which occur at the same time (2 P. M. ), are as follows (in kwh): city 1— 45 million; city 2— 20 million; city 3— 30 million; city 4— 30 million. • The costs of sending 1 million kwh of electricity from plant to city depend on the distance the electricity must travel as in the following table. • Formulate an LP to minimize the cost of meeting each city’s peak power demand. 18/4/2019 CSE 324 OR: Lec 09 3

Transportation Problem (2) Powerco Example • Each power plant is called a supply point. • Each city is called a demand point. 18/4/2019 CSE 324 OR: Lec 09 4

Transportation Problem (3) Powerco LP Formulation • Decision variables: • Objective function: The total cost of supplying the peak power demands to the four cities as: 18/4/2019 CSE 324 OR: Lec 09 5

Transportation Problem (4) Powerco Constraints • Supply constraints: Ensure that the total quantity shipped from each plant does not exceed plant capacity. • Demand constraints: Ensure that each city will receive sufficient power to meet its peak demand. 18/4/2019 CSE 324 OR: Lec 09 6

Transportation Problem (5) Powerco LP Formulation 18/4/2019 CSE 324 OR: Lec 09 7

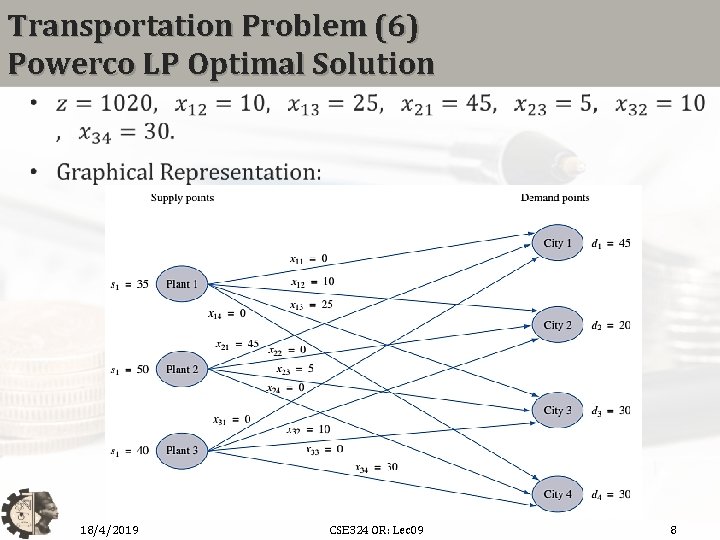
Transportation Problem (6) Powerco LP Optimal Solution 18/4/2019 CSE 324 OR: Lec 09 8

General Description of a Transportation Problem (1) 18/4/2019 CSE 324 OR: Lec 09 9

General Description of a Transportation Problem (2) • Then, LP formulation for general transportation problem is: • A balanced transportation problem has: • Then, the constraints of the balanced transportation problem are: 18/4/2019 CSE 324 OR: Lec 09 10

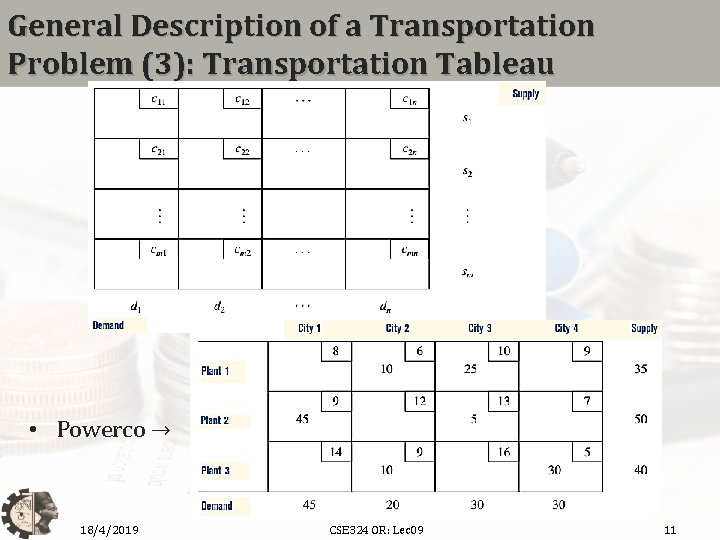
General Description of a Transportation Problem (3): Transportation Tableau • Powerco → 18/4/2019 CSE 324 OR: Lec 09 11

Finding bfs for Transportation Problems • Three methods that can be used to find a basic feasible solution for a balanced transportation problem: 1. Northwest corner method. 2. Minimum-cost method. 3. Vogel’s method. • These methods just find a bfs not an optimal solution. 18/4/2019 CSE 324 OR: Lec 09 12

Northwest Corner Method (1) 18/4/2019 CSE 324 OR: Lec 09 13

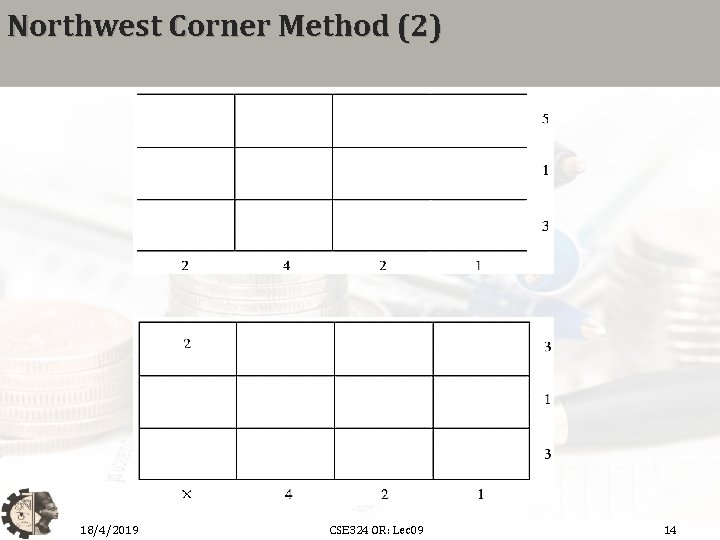
Northwest Corner Method (2) 18/4/2019 CSE 324 OR: Lec 09 14

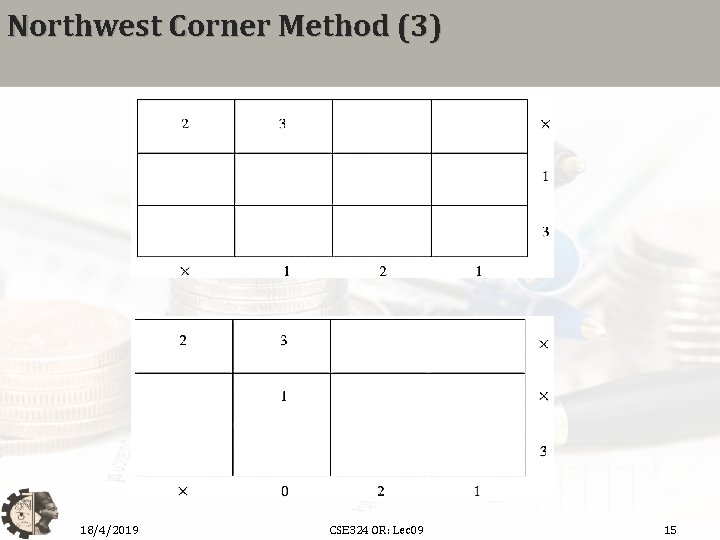
Northwest Corner Method (3) 18/4/2019 CSE 324 OR: Lec 09 15

Northwest Corner Method (4) 18/4/2019 CSE 324 OR: Lec 09 16

Minimum-cost (Least-cost) Method (1) 18/4/2019 CSE 324 OR: Lec 09 17

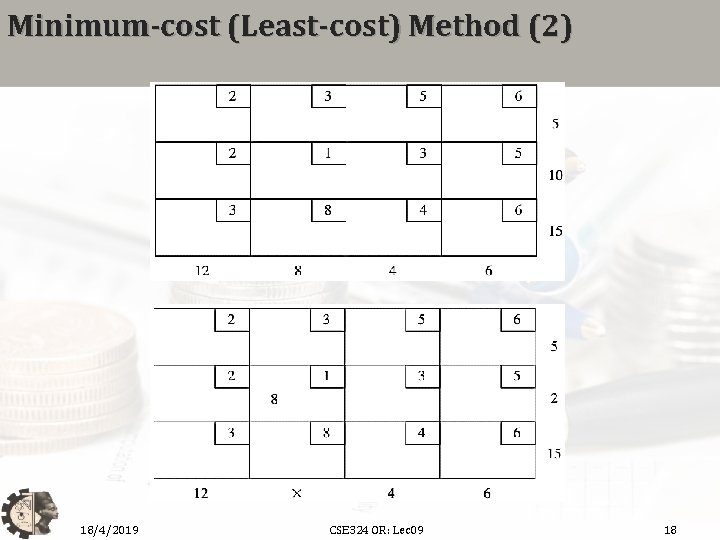
Minimum-cost (Least-cost) Method (2) 18/4/2019 CSE 324 OR: Lec 09 18

Minimum-cost (Least-cost) Method (3) 18/4/2019 CSE 324 OR: Lec 09 19

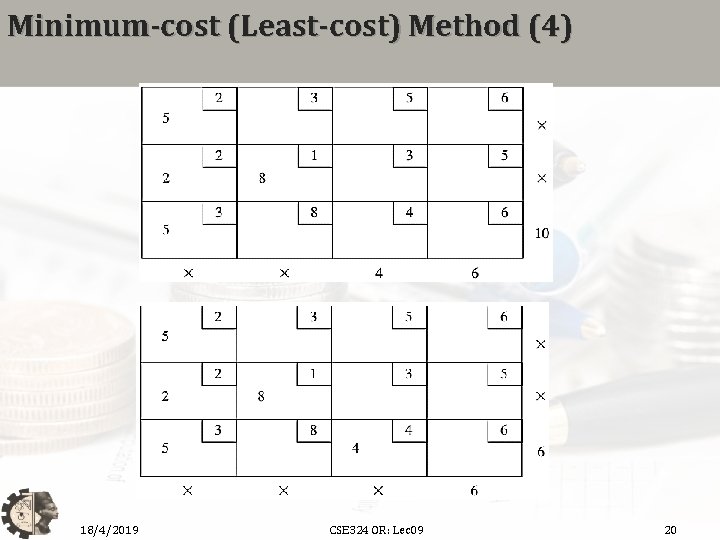
Minimum-cost (Least-cost) Method (4) 18/4/2019 CSE 324 OR: Lec 09 20

Minimum-cost (Least-cost) Method (5) 18/4/2019 CSE 324 OR: Lec 09 21

Vogel’s Method (1) 18/4/2019 CSE 324 OR: Lec 09 22

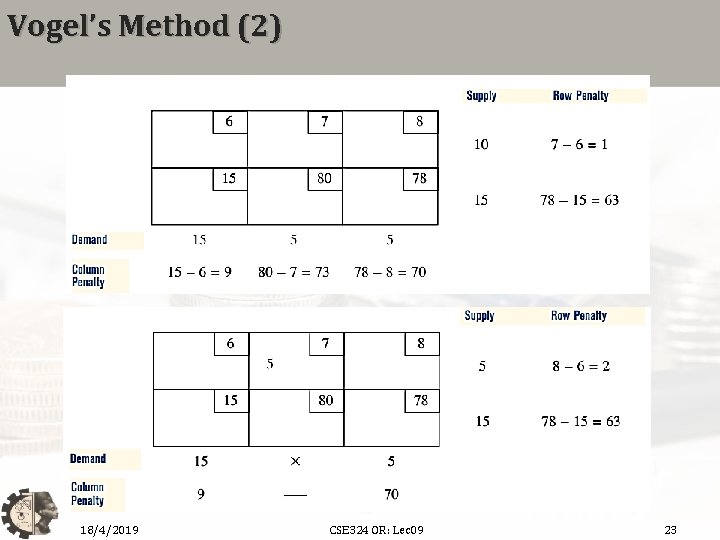
Vogel’s Method (2) 18/4/2019 CSE 324 OR: Lec 09 23

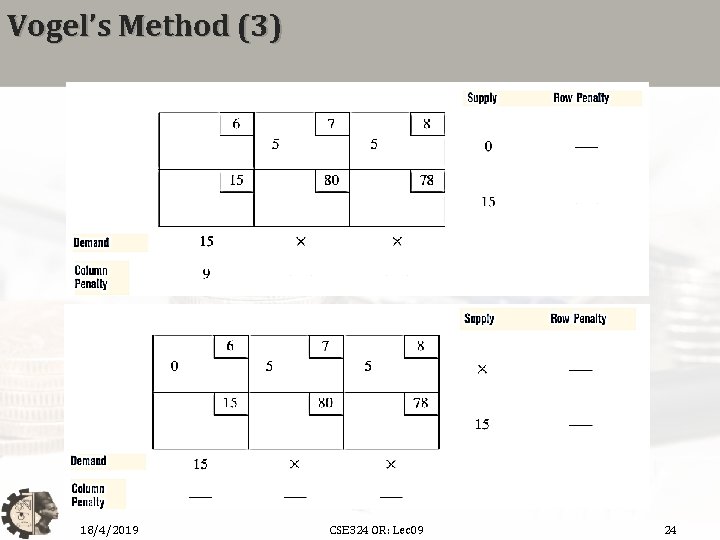
Vogel’s Method (3) 18/4/2019 CSE 324 OR: Lec 09 24

Comparing bfs for Transportation Problems 1. Northwest corner method: Requires least computational effort but doesn’t utilize cost information and can lead to a bfs with extremely high cost. 2. Minimum-cost method: Utilizes cost information but also can lead to a bfs with extremely high cost. 3. Vogel’s method: Avoids bfs with high cost, but at more computational efforts. 18/4/2019 CSE 324 OR: Lec 09 25