CSE 321 Discrete Structures Winter 2008 Lecture 1

























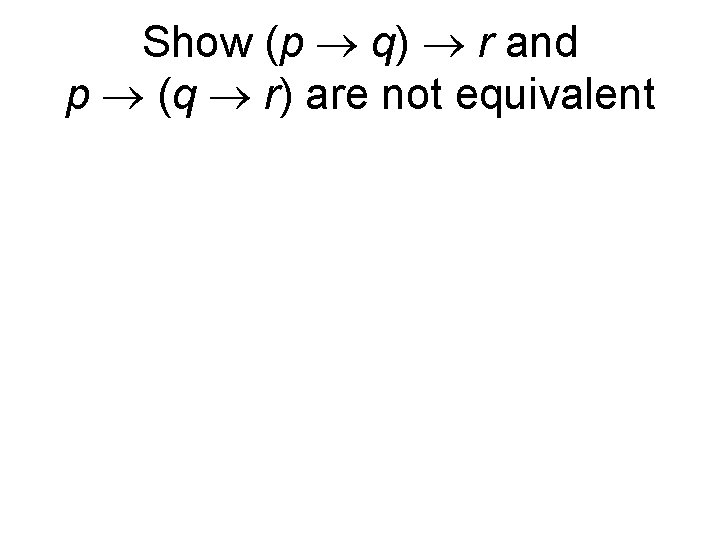










- Slides: 39

CSE 321 Discrete Structures Winter 2008 Lecture 1 Propositional Logic

About the course • From the CSE catalog: – CSE 321 Discrete Structures (4) Fundamentals of set theory, graph theory, enumeration, and algebraic structures, with applications in computing. Prerequisite: CSE 143; either MATH 126, MATH 129, or MATH 136. • What I think the course is about: – Foundational structures for the practice of computer science and engineering

Why this material is important • Language and formalism for expressing ideas in computing • Fundamental tasks in computing – Translating imprecise specification into a working system – Getting the details right

Topic List • Logic/boolean algebra: hardware design, testing, artificial intelligence, software engineering • Mathematical reasoning/induction: algorithm design, programming languages • Number theory/probability: cryptography, security, algorithm design, machine learning • Relations/relational algebra: databases • Graph theory: networking, social networks, optimization

Administration • Instructor – Richard Anderson • Teaching Assistant – Natalie Linnell • Quiz section – Thursday, 12: 30 – 1: 20, or 1: 30 – 2: 20 – CSE 305 • Recorded Lectures – Available on line • Text: Rosen, Discrete Mathematics – 6 th Edition preferred – 5 th Edition okay • Homework – Due Wednesdays (starting Jan 16) • Exams – Midterms, Feb 8 – Final, March 17, 2: 30 -4: 20 pm • All course information posted on the web • Sign up for the course mailing list

Propositional Logic

Propositions • A statement that has a truth value • Which of the following are propositions? – – – – The Washington State flag is red It snowed in Whistler, BC on January 4, 2008. Hillary Clinton won the democratic caucus in Iowa Space aliens landed in Roswell, New Mexico Ron Paul would be a great president Turn your homework in on Wednesday Why are we taking this class? If n is an integer greater than two, then the equation an + bn = cn has no solutions in non-zero integers a, b, and c. – Every even integer greater than two can be written as the sum of two primes – This statement is false – Propositional variables: p, q, r, s, . . . – Truth values: T for true, F for false

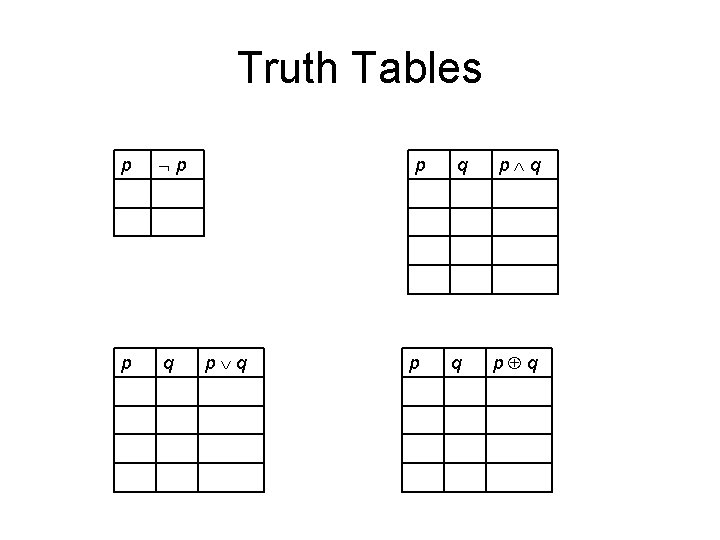
Compound Propositions • • • Negation (not) Conjunction (and) Disjunction (or) Exclusive or Implication Biconditional p p q p q p q

Truth Tables p p p q p q

Understanding complex propositions • Either Harry finds the locket and Ron breaks his wand or Fred will not open a joke shop

Understanding complex propositions with a truth table h r f h r f (h r) f

Aside: Number of binary operators • How many different binary operators are there on atomic propositions?

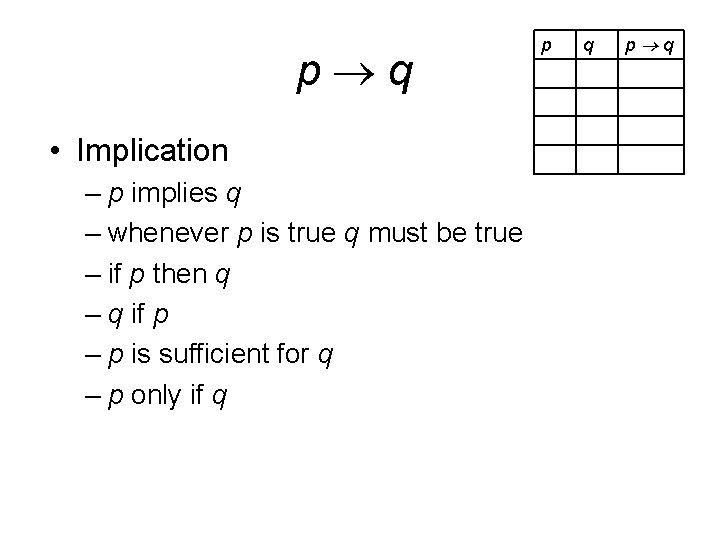
p q • Implication – p implies q – whenever p is true q must be true – if p then q – q if p – p is sufficient for q – p only if q p q

If pigs can whistle then horses can fly

Converse, Contrapositive, Inverse • • Implication: p q Converse: q p Contrapositive: q p Inverse: p q • Are these the same?

Biconditional p q • p iff q • p is equivalent to q • p implies q and q implies p p q

English and Logic • You cannot ride the roller coaster if you are under 4 feet tall unless you are older than 16 years old – q: you can ride the roller coaster – r: you are under 4 feet tall – s: you are older than 16

Logical equivalence • Terminology: A compound proposition is a – Tautology if it is always true – Contradiction if it is always false – Contingency if it can be either true or false p p (p p) p p p q q (p q) p (p q) (p q) ( p q)

Logical Equivalence • p and q are Logically Equivalent if p q is a tautology. • The notation p q denotes p and q are logically equivalent • Example: (p q) ( p q) p q p p q (p q) ( p q)

Computing equivalence • Describe an algorithm for computing if two logical expressions are equivalent • What is the run time of the algorithm?

Understanding connectives • Reflect basic rules of reasoning and logic • Allow manipulation of logical formulas – Simplification – Testing for equivalence • Applications – Query optimization – Search optimization and caching – Artificial Intelligence – Program verification

Properties of logical connectives • • Identity Domination Idempotent Commutative Associative Distributive Absorption Negation

De Morgan’s Laws • (p q) p q • What are the negations of: – Casey has a laptop and Jena has an i. Pod – Clinton will win Iowa or New Hampshire

Equivalences relating to implication • • p q p q q p p q p q (p q) p q (p q) (q p) p q p q (p q) ( p q) (p q) p q

Logical Proofs • To show P is equivalent to Q – Apply a series of logical equivalences to subexpressions to convert P to Q • To show P is a tautology – Apply a series of logical equivalences to subexpressions to convert P to T

Why bother with logical proofs when we have truth tables?

Show (p q) is a tautology
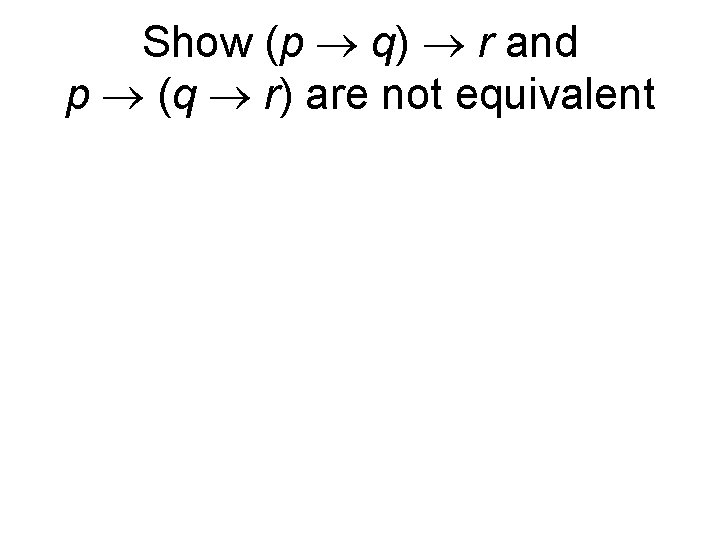
Show (p q) r and p (q r) are not equivalent

Predicate Calculus • Predicate or Propositional Function – A function that returns a truth value • • • “x is a cat” “x is prime” “student x has taken course y” “x > y” “x + y = z”

Quantifiers • x P(x) : P(x) is true for every x in the domain • x P(x) : There is an x in the domain for which P(x) is true

Statements with quantifiers • x Even(x) • x Odd(x) • x (Even(x) Odd(x)) • x Greater(x+1, x) • x (Even(x) Prime(x)) Domain: Positive Integers Even(x) Odd(x) Prime(x) Greater(x, y) Equal(x, y)

Statements with quantifiers • x y Greater (y, x) For every number there is some number that is greater than it • y x Greater (y, x) • x y (Greater(y, x) Prime(y)) • x (Prime(x) (Equal(x, 2) Odd(x)) • x y(Equal(x, y + 2) Prime(x) Prime(y)) Domain: Positive Integers Greater(a, b) “a > b”

Statements with quantifiers • “There is an odd prime” Domain: Positive Integers • “If x is greater than two, x is not an even prime” Even(x) Odd(x) Prime(x) Greater(x, y) Equal(x, y) • x y z ((Equal(z, x+y) Odd(x) Odd(y)) Even(z)) • “There exists an odd integer that is the sum of two primes”

Goldbach’s Conjecture • Every even integer greater than two can be expressed as the sum of two primes Even(x) Odd(x) Prime(x) Greater(x, y) Equal(x, y) Domain: Positive Integers

Systems vulnerability Reasoning about machine status • Specify systems state and policy with logic – Formal domain • reasoning about security • automatic implementation of policies • Domains – Machines in the organization – Operating Systems – Versions – Vulnerabilities – Security warnings • Predicates – – – Runs. OS(M, O) Vulnerable(M) OSVersion(M, Ve) Later. Version(Ve, Ve) Unpatched(M)

System vulnerability statements • Unpatched machines are vulnerable • There is an unpatched Linux machine • All Windows machines have versions later than SP 1

Prolog • Logic programming language • Facts and Rules Runs. OS(Slipper. PC, Windows) Runs. OS(Slipper. Tablet, Windows) Runs. OS(Carmel. Laptop, Linux) OSVersion(Slipper. PC, SP 2) OSVersion(Slipper. Tablet, SP 1) OSVersion(Carmel. Laptop, Ver 3) Later. Version(SP 2, SP 1) Later. Version(Ver 3, Ver 2) Later. Version(Ver 2, Ver 1) Later(x, y) : Later(x, z), Later(z, y) Not. Later(x, y) : - Later(y, x) Not. Later(x, y) : Same. Version(x, y) Machine. Vulnerable(m) : OSVersion(m, v), Version. Vulnerable(v) : Critical. Vulnerability(x), Version(x, n), Not. Later(v, n)

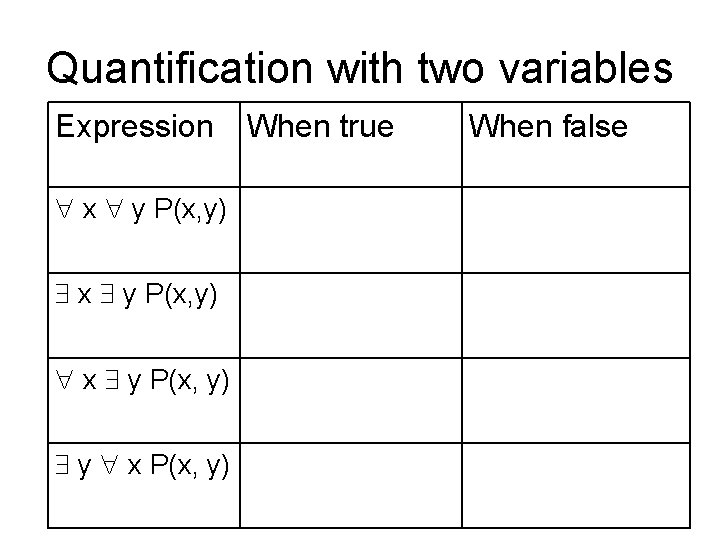
Nested Quantifiers • Iteration over multiple variables • Nested loops • Details – Use distinct variables • x( y(P(x, y) x Q(y, x))) – Variable name doesn’t matter • x y P(x, y) a b P(a, b) – Positions of quantifiers can change (but order is important) • x (Q(x) y P(x, y)) x y (Q(x) P(x, y))

Quantification with two variables Expression x y P(x, y) y x P(x, y) When true When false