CSE 291 Numerical Methods Matrix Computations Iterative Methods

CSE 291: Numerical Methods Matrix Computations: Iterative Methods I Chung-Kuan Cheng

Outline o Introduction o Direct Methods o Iterative Methods n n n Formulations Projection Methods Krylov Space Methods Preconditioned Iterations Multigrid Methods Domain Decomposition Methods 2

Introduction Iterative Methods Direct Method LU Decomposition Domain Decomposition General and Robust but can be complicated if N>= 1 M Preconditioning Conjugate Gradient Jacobi GMRES Multigrid Gauss-Seidel Excellent choice for SPD matrices Remain an art for arbitrary matrices 3

Introduction: Matrix Condition 4

Introduction: Matrix norm 5

Introduction: Scaling 6

Introduction: Gershgorin Circle Theorem 7

Gershgorin Circle Theorem: Example 2 0. 1 0. 2 0. 3 0. 1 3 0 0. 3 4 0. 1 0 0 0. 2 5 8

Iterative Methods o 9

Stationary: Jacobi Method 10

Stationary-Gause-Seidel 11

Stationary: Successive Overrelaxation (SOR) Devised by extrapolation applied to Gauss-Seidel in the form of weighted average: In matrix terms the method becomes: where D, -L and -U represent the diagonal, the strictly lowertrg and strictly upper-trg parts of M M=D-L-U 12

SOR o Choose w to accelerate the convergence n W =1 : Jacobi / Gauss-Seidel n 2>W>1: Over-Relaxation n W < 1: Under-Relaxation 13

Convergence of Stationary Method o 14

Convergence of Gauss-Seidel o 15

Linear Equation: an optimization problem o 16

Linear Equation: an optimization problem o 17

18

Gradient of quadratic form 19

o since We have, If p != x 20

If A is not positive definite a) Positive definite matrix b) negative-definite matrix c) Singular matrix d) positive indefinite matrix 21

Non-stationary Iterative Method o State from initial guess x 0, adjust it until close enough to the exact solution i=0, 1, 2, 3, …… Adjustment Direction Step Size o How to choose direction and step size? 22

Steepest Descent Method (1) o Choose the direction in which f decrease most quickly: the direction opposite of o Which is also the direction of residue 23

Steepest Descent Method (2) o How to choose step size ? n Line Search should minimize f, along the direction of , which means Orthogonal 24

Steepest Descent Algorithm Given x 0, iterate until residue is smaller than error tolerance 25

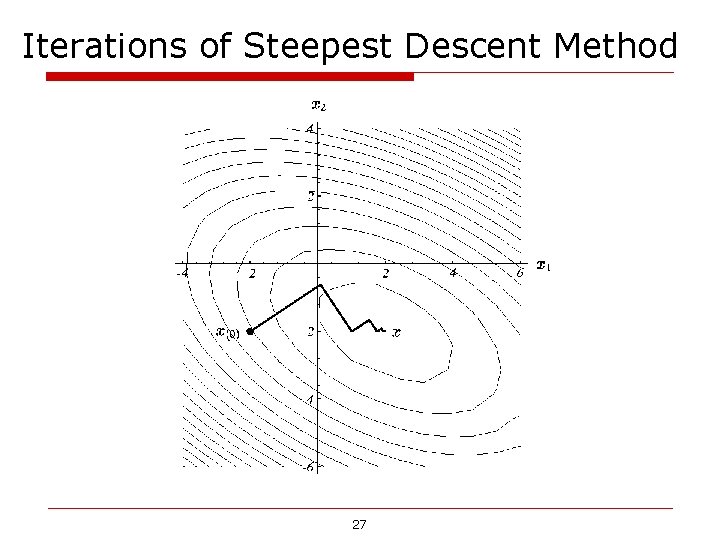
Steepest Descent Method: example a) Starting at (-2, -2) take the direction of steepest descent of f b) Find the point on the intersection of these two surfaces that minimize f c) Intersection of surfaces. d) The gradient at the bottommost point is orthogonal to the gradient of the previous step 26

Iterations of Steepest Descent Method 27

Convergence of Steepest Descent-1 Eigenvector: Eigen. Value: j=1, 2, …, n Energy norm: 28

Convergence of Steepest Descent-2 29

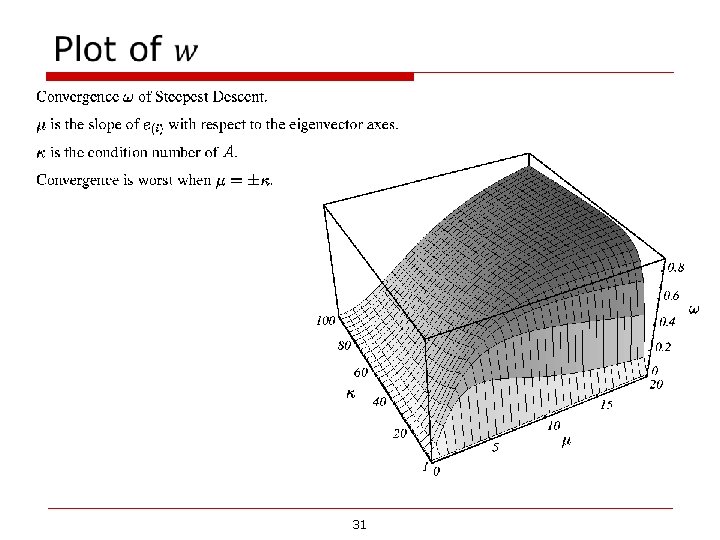
Convergence Study (n=2) assume let Spectral condition number let 30

31

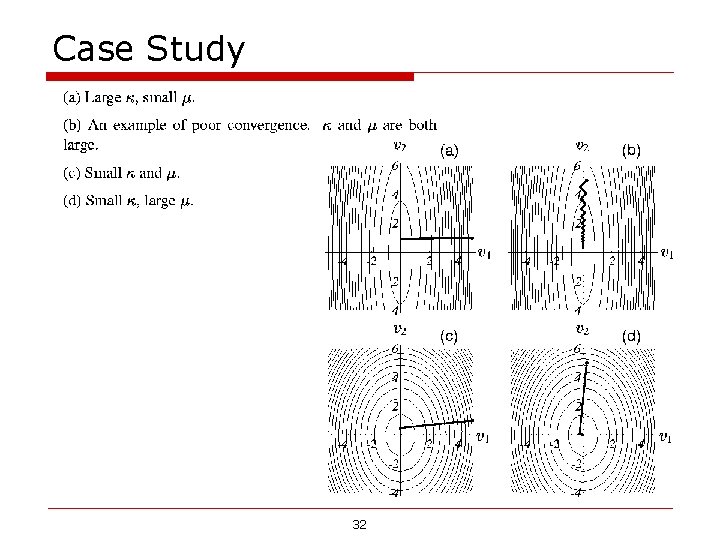
Case Study 32

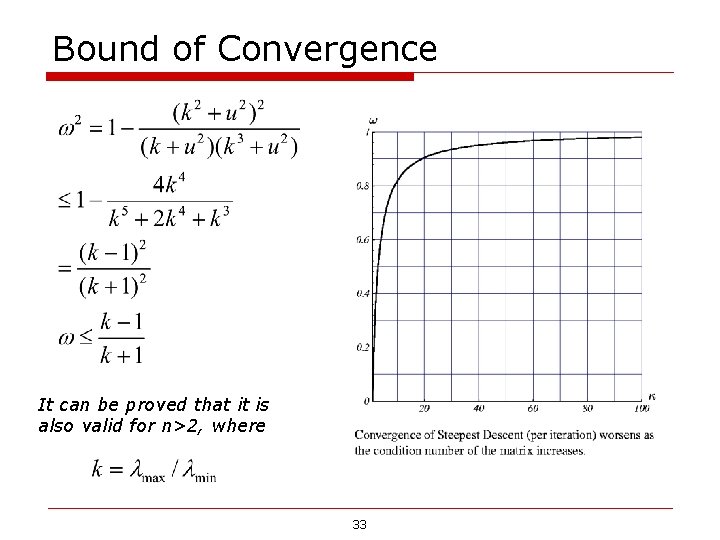
Bound of Convergence It can be proved that it is also valid for n>2, where 33