CSE 246 Computer Arithmetic Algorithms and Hardware Design

CSE 246: Computer Arithmetic Algorithms and Hardware Design Fall 2006 Lecture 9: Floating Point Numbers Instructor: Prof. Chung-Kuan Cheng CSE 246

Motivation o o Maximal information with given bit numbers. Arithmetic with proper precision. Fairness of rounding. Features at the expenses of the complexity of the operations. CSE 246 2

Topics: § Floating Point Numbers (IEEE P 754) q q Standard Operations Exceptional Situations Rounding Modes q Numerical Computing with IEEE Floating Point Arithmetic, Michael L. Overton, SIAM CSE 246 3

Standard 232 Typically §Goal: Dynamic Range: largest #/ smallest # §If too large, holes between #’s CSE 246 4

Standard § ulp (unit in the last place) § Difference between two consecutive values of the significand. 3 Parts x = ~s be: sign, significand, exponent Sign Bit 23 -bit Significand 8 -bit exponent CSE 246 5

Standard ~e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 s 1 s 2 s 3…s 22 s 23 o n n n 1. s 1 s 2 s 3…s 22 s 23 normalized number 0. s 1 s 2 s 3…s 22 s 23 denormalized number e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 00000001 00000010 0 x=0. s 1 s 2 s 3…s 22 s 23 2 -126 1 x=1. s 1 s 2 s 3…s 22 s 23 2 -126 2 x=1. s 1 s 2 s 3…s 22 s 23 2 -125. 127 0 1 1 1 1 x=1. s 1 s 2 s 3…s 22 s 23 20. 253 1 1 1 0 1 x=1. s 1 s 2 s 3…s 22 s 23 2126 254 11111110 x=1. s 1 s 2 s 3…s 22 s 23 2127 255 1111 x= Inf if (s 1 …s 23)= 0, Na. N otherwise. Na. N Not a Number CSE 246 6

Standard 0. 01 x 2 -3 = 0. 001 x 2 -2 § Same number, so normalize to remove redundancy § Use a default 1 in front for one more bit precision. § Smallest Number 0. 00… 01 x 2 -126 = 1. 0 x 2 -23 x 2 -126 = 1 x 2 -149 CSE 246 7

Standard - Example ~ eeee sssss sss 0 000000000000000 = 0. 000… 0 x 2 -126 1 0000000000000000 =-0. 000… 0 x 2 -126 0 0000000000000001 = 0. 000… 1 x 2 -149 0 00000001 000000000000 = 1. 000… 0 x 2 -126 normalized minimum 0 00000001 000000000001 = 1. 000… 1 x 2 -126. . 0 01111111 000000000000 = 1. 000… 0 x 2 0 0 01111111 000000000001 = 1. 000… 1 x 2 0 0 1000000000001 = 1. 000… 1 x 2 1 CSE 246 8

Standard – Example Cont. 0 11111110 000000000000 = 1. 000… 0 x 2 127 0 11111110 000000000001 = 1. 000… 1 x 2 127 0 111111111111111 = 1. 111… 1 x 2 127 - Normalized Maximum 0 1111 000000000000 = Inf Nmin = 1. 0 x 2 -126 Nmax = (2 – 2 -23)2127 CSE 246 9

Double Floating Point ~ e 1 e 2…e 11 s 1 s 2…s 52 0 00… 000 s 1 s 2…s 52 x=0. s 1 s 2…s 52 2 -1022 0 00… 001 s 1 s 2…s 52 x=1. s 1 s 2…s 52 2 -1022. . 0 01… 111 s 1 s 2…s 52 x=1. s 1 s 2…s 52 20 0 10… 000 s 1 s 2…s 52 x=1. s 1 s 2…s 52 21. . 0 11… 110 s 1 s 2…s 52 0 11… 111 s 1 s 2…s 52 CSE 246 x=1. s 1 s 2…s 52 21023 x=Inf if (s 1…s 52)=0 10

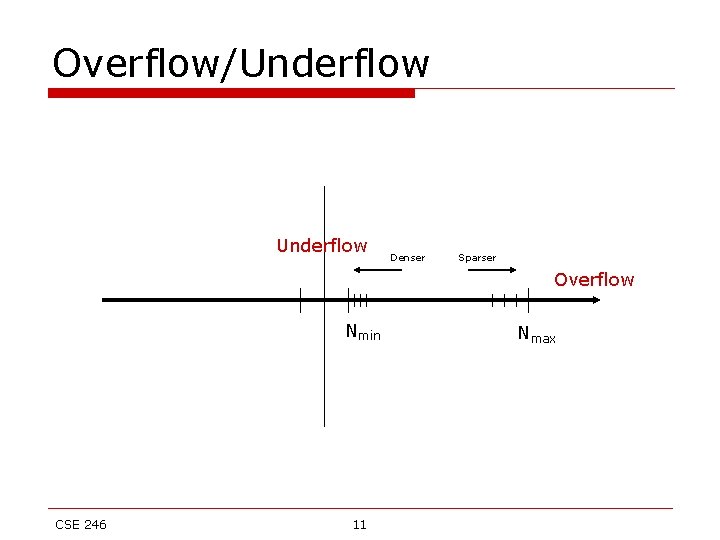
Overflow/Underflow Denser Sparser Overflow Nmin CSE 246 11 Nmax

Addition/Multiplication o ~s 1 xbe 1 + (~s 2 xbe 2) = ~sxbe = ~s 1 xbe 1 + ~s 2/be 1 -e 2 x be 1 = (~s 1 + ~s 2/be 1 -e 2) x be 1 o (~s 1 xbe 1) x (~s 2 xbe 2) = ~(s 1 xs 2)be 1+e 2 CSE 246 12

Exceptions a/0 = Inf if a > 0 a/Inf = 0 if a != 0 a· 0 = 0 a·Inf = Inf if a > 0 a + Inf = Inf 0·Inf = invalid operation (Na. N) 0/0 = invalid operation (Na. N) Inf - Inf = Na. N Na. P op a = Na. N CSE 246 13

Rounding Mode o Adder Output = Cout z 1 z 0. z-1 z-2…z-l GRS Guard Bit Round Bit Sticky Bit, OR of all bits below bit R 1. 101 x 23 +1. 110 x 23 11. 011 x 23 1. 1011 x 24 CSE 246 Normalize – need to round 14 or

Rouding 1. 110 - 1. 101 0. 001 1. 000 23 23 23 20 1. 101 23 - 1. 111 22 1. 101 23 - 0. 1101 23 1. 101 22 CSE 246 normalize Guard bit 15

Rounding o Round to the nearest even n n CSE 246 1. 10111 toward 0 1. 1011 Toward +Inf 1. 1100 Toward -Inf 1. 1011 16

Conventional Rounding Error Rounding 1. 10100 1. 10101 1. 10110 1. 10111 1. 101 1. 110 Error = = 0 -0. 25 +0. 25 Average Error = 0. 5/4 = 0. 125 CSE 246 17