CSE 246 Adder Part I Instructor Prof ChungKuan

CSE 246 Adder – Part I Instructor: Prof. Chung-Kuan Cheng

Framework o Adder Design Specification n n o Adder Design Optimization n n o Half/Full adder Carry ripple adder Circuit level – Asynchronous adder, Manchester adder Logic level – carry look adder, Ling’s adder, etc… Algorithm level – prefix adders o Generic parallel prefix adder optimization using dynamic programming o Zero-deficiency prefix adder Function level – carry skip adder Multi-operand Addition 11/27/2020 2

Half Adder o Half Adder n n n “half” means no carry-in Input: x i, y i Sum: si = xi⊕yi Carry out: ci+1 = xiyi Notation: o o o 11/27/2020 ⊕ means logical XOR + means logical OR Juxtaposition means logical AND 3

Full Adder o o Input: xi, yi and carry-in ci Output n n si = xi⊕yi⊕ci ci+1 = xiyi + ci(xi+yi) = xiyi + ci(xi⊕yi) 11/27/2020 4

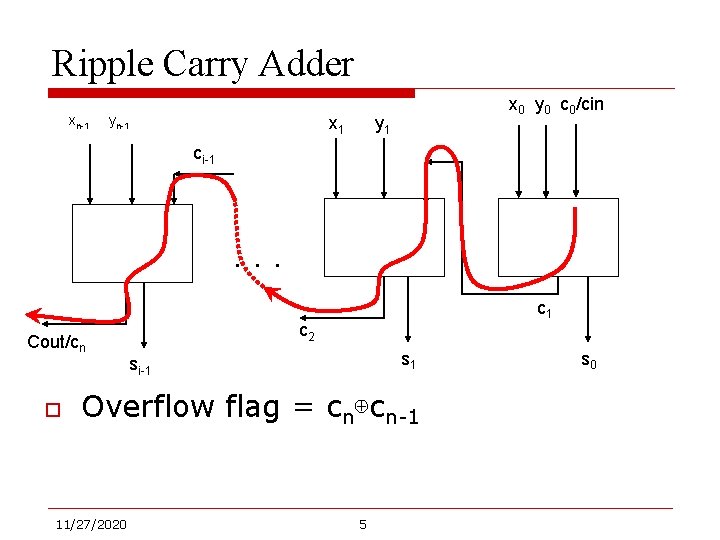
Ripple Carry Adder xn-1 yn-1 x 0 y 0 c 0/cin y 1 ci-1 . . . Cout/cn o c 1 c 2 s 1 si-1 Overflow flag = cn⊕cn-1 11/27/2020 5 s 0

Understanding Carry Ripple Chain o o o Carry generation signal gi = x i y i Carry propagation signal pi = xi⊕yi Carry annihilation signal ai = (xi+yi)’ Carry ripple in terms of p, g ci+1 = gi + pici In practice, we might use ti = xi+yi = pi+gi and ci+1=gi+tici 11/27/2020 6

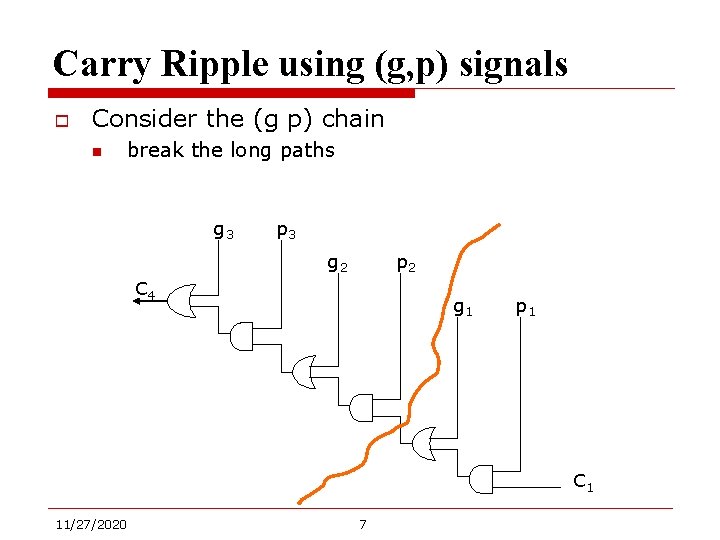
Carry Ripple using (g, p) signals o Consider the (g p) chain n break the long paths g 3 p 3 g 2 p 2 C 4 g 1 p 1 C 1 11/27/2020 7

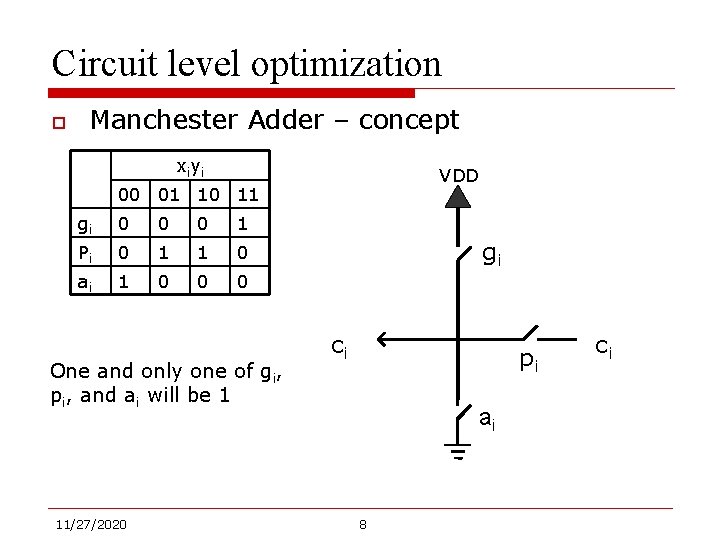
Circuit level optimization o Manchester Adder – concept xiyi VDD 00 01 10 11 gi 0 0 0 1 Pi 0 1 1 0 ai 1 0 0 0 One and only one of gi, pi, and ai will be 1 11/27/2020 gi ci pi ai 8 ci

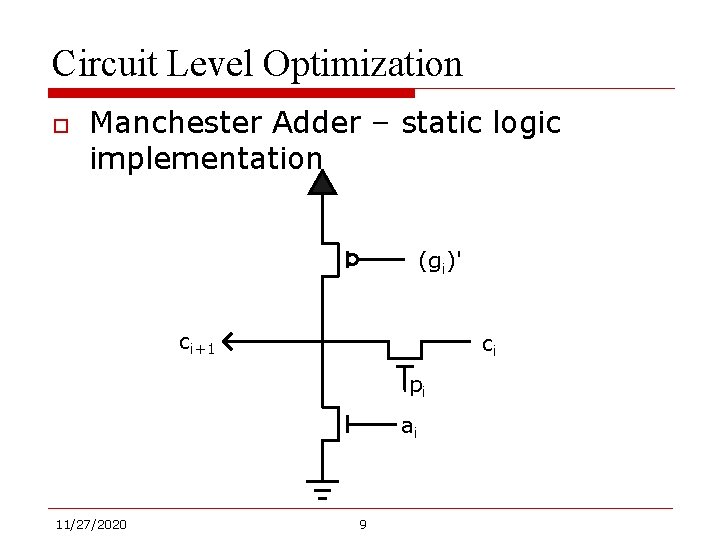
Circuit Level Optimization o Manchester Adder – static logic implementation (gi)' ci+1 ci pi ai 11/27/2020 9

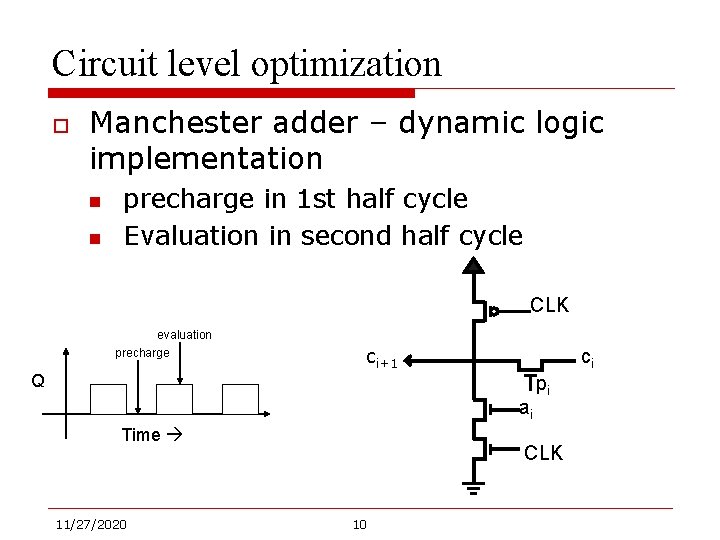
Circuit level optimization o Manchester adder – dynamic logic implementation n n precharge in 1 st half cycle Evaluation in second half cycle CLK evaluation precharge Q ci+1 ci ai Time 11/27/2020 pi CLK 10

Logic level optimization o Carry look ahead adder Instead of generating carries bit-by-bit, try to look ahead to generate a group of consecutive carries simultaneously n Use logic manipulation to save hardware n Recursively unroll ci=gi-1+pi-1 ci-1 ci=gi-1+pi-1 gi-2+pi-1 pi-2 ci-2 n ci=gi-1+pi-1 gi-2+pi-1 pi-2 gi-3+pi-1 pi-2 pi-3 gi-4+pi-1 pi-2 pi-3 pi-4 ci-4 11/27/2020 11

Logic level optimization o Ling’s adder n Notice gi=gipi ci =pi-1(gi-1+gi-2+pi-2 gi-3+pi-2 pi-3 gi-4+pi-2 pi-3 pi-4 ci-4) n Use ti instead of pi ci=ti-1(gi-1+gi-2+ti-2 gi-3+ti-2 ti-3 gi-4+ti-2 ti-3 ti-4 ci-4) n Define the expression in parenthesis to be hi o o 11/27/2020 ci =ti-1 hi hi = gi-1+gi-2+ti-2 gi-3+ti-2 ti-3 gi-4+ti-2 ti-3 ti-4 ti-5 hi-4 12

Asynchronous Adder o Carry completion detection 11/27/2020 ci bi Remark 0 0 Not complete 1 0 Complete 0 1 Complete 1 1 Don’t care 13

Group (G, P) signals o Generating g[3: 2] and g[3: 2] g 3 p 3 g 2 p 2 g 1 p 1 C 4 g 3 p 3 g 2 p 2 C 1 g[3: 2] p[3: 2] 11/27/2020 14

Group (G, P) signals Generating g[1: 0] and p[1: 0] o g 3 p 3 g 2 p 2 g 1 p 1 C 4 g 1 p 1 cin g[1: 0] p[1: 0 ] 11/27/2020 15

Group (G, P) signals o Generating g[3: 0] and p[3: 0] g 3 p 3 g 1 p 1 g 2 p 2 G[3: 2] P[3: 2] g[3: 2] p[3: 2] g[1: 0] g[3: 0] p[1: 0 ] g[1: 0] p[3: 0] p[1: 0 ] 11/27/2020 16 cin

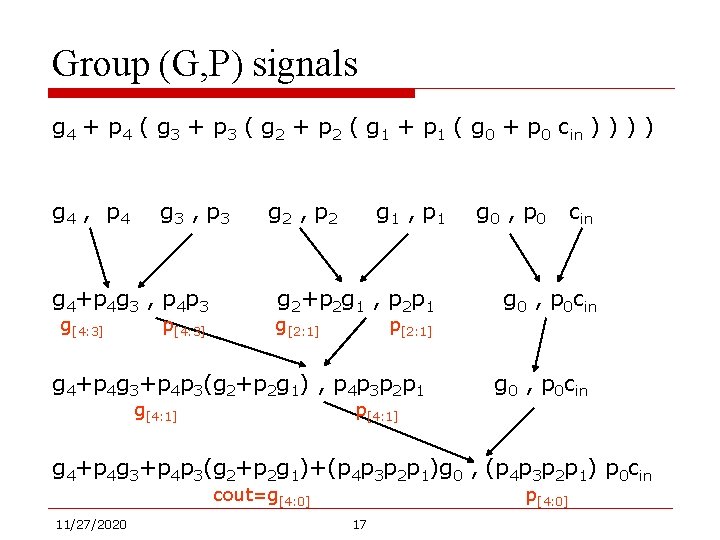
Group (G, P) signals g 4 + p 4 ( g 3 + p 3 ( g 2 + p 2 ( g 1 + p 1 ( g 0 + p 0 cin ) ) g 4 , p 4 g 3 , p 3 g 4+p 4 g 3 , p 4 p 3 g[4: 3] p[4: 3] g 2 , p 2 g 1 , p 1 g 2+p 2 g 1 , p 2 p 1 g[2: 1] p[2: 1] g 4+p 4 g 3+p 4 p 3(g 2+p 2 g 1) , p 4 p 3 p 2 p 1 g[4: 1] p[4: 1] g 0 , p 0 cin g 0 , p 0 cin g 4+p 4 g 3+p 4 p 3(g 2+p 2 g 1)+(p 4 p 3 p 2 p 1)g 0 , (p 4 p 3 p 2 p 1) p 0 cin cout=g[4: 0] 11/27/2020 p[4: 0] 17

Parallel Prefix Adder o o What is parallel prefix problem? How binary addition is modeled as a parallel prefix problem? 11/27/2020 18

Parallel Prefix Problem (PPP) Given n inputs which can be either scalars or vectors, and an arbitrary associative operator • , compute the products for 11/27/2020 19

Parallel Prefix Problem o Direct example is prefix sum problem n n • is simply natural addition yi = xi+xi-1+…+x 1 for Partial sum n n n 11/27/2020 s[i: j]=xi+xj-1+…+xj (n≥j≥i≥ 1) yn = s[n: 1] = xn+xn-1+…+x 1 yn-1= s[n-1: 1] = xn-1+…+x 1 … y 2 = s[2: 1] = x 2+x 1 y 1 = s[1: 1] = x 1 20

Binary addition as a PPP Addends: Sum: Carry generation signals: Carry propagation signals: Carry bits: Sum bits: 11/27/2020 21

Binary Addition as a PPP Block carry generation signal Block carry propagation signal Introducing (P, G) operator The calculation of (P, G) pairs becomes a prefix problem 11/27/2020 22

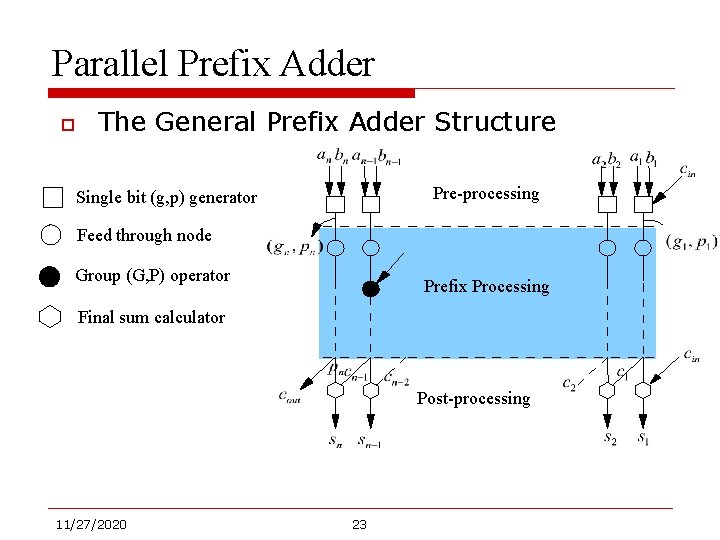
Parallel Prefix Adder o The General Prefix Adder Structure Pre-processing Single bit (g, p) generator Feed through node Group (G, P) operator Prefix Processing Final sum calculator Post-processing 11/27/2020 23

Prefix Adder: Graph Representation o o o strictly leveled directed acyclic graph (DAG) of n columns Size = number of computation (black) nodes Depth = level of the latest output Serial Prefix Circuit 11/27/2020 24

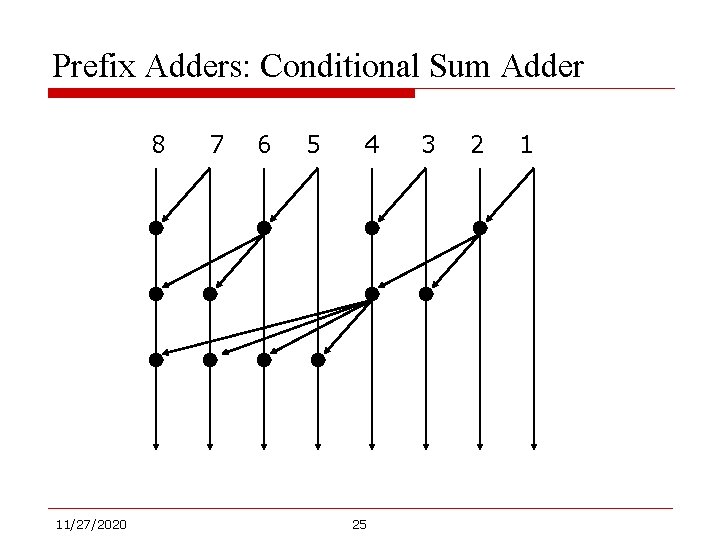
Prefix Adders: Conditional Sum Adder 8 11/27/2020 7 6 5 4 25 3 2 1

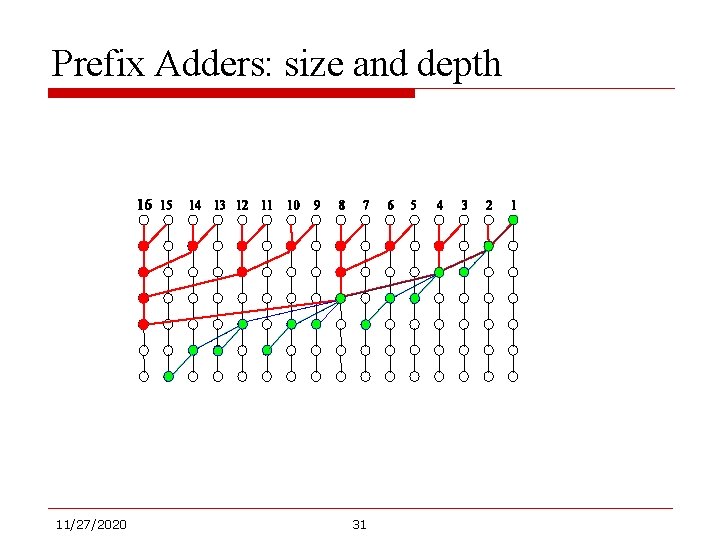
Prefix Adders: size and depth o Objective: n n o Minimize # of nodes, sc(n). Minimize depth, dc(n) Tradeoff between size and depth n Ripple Carry Adder: o o o n sc(8) = 7 dc(8) = 7 total = 14 Conditional Sum Adder: o o o 11/27/2020 sc(8) = 12 dc(8) = 3 total = 15 26

Prefix Adders: size and depth o o o Minimum size = n-1, achieved by prefix adder Minimum depth = ceil(log(n)), achieved by conditional sum adder Given depth constraint, what is the minimum size? 11/27/2020 27

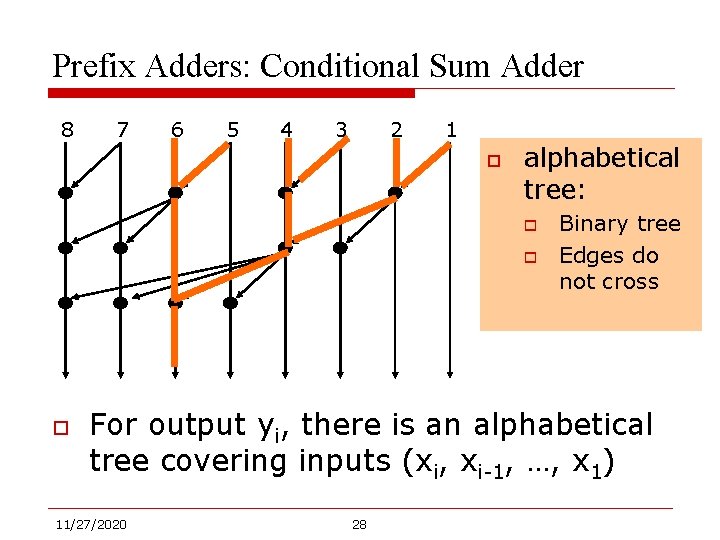
Prefix Adders: Conditional Sum Adder 8 7 6 5 4 3 2 1 o alphabetical tree: o o o Binary tree Edges do not cross For output yi, there is an alphabetical tree covering inputs (xi, xi-1, …, x 1) 11/27/2020 28

Prefix Adders: Conditional Sum Adder 8 7 6 5 4 3 2 1 The nodes in this tree can be reduced to (g, p) o c = g+pc o o From input x 1, there is a tree covering all outputs (yi, yi-1, …, y 1) 11/27/2020 29

Prefix Adders: size and depth o Theorem: sc(n)+dnc(n) >= 2 n-2 n o dnc(n) means the depth of the last output Proof: n n Alphabetical tree of yn contains n-1 internal nodes. For each column where the prefix is not ready, at lease one extra node is needed, therefore we need at least n-(dnc(n) +1) extra nodes sc(n) >=n-1+(n–(dnc(n)+1))=2 n-2 -dnc(n) sc(n) + dnc(n) >= 2 n-2 11/27/2020 30

Prefix Adders: size and depth 11/27/2020 31

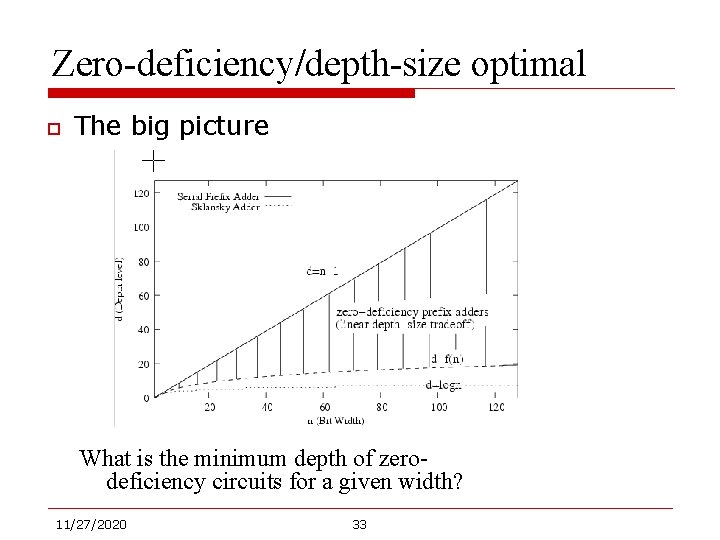
Zero-deficiency/depth-size optimal o o o Define the deficiency of a prefix circuit is as def = size + depth – (2 n – 2) A prefix circuit is said to be of zero-deficiency if its deficiency is zero A prefix circuit is said to be depth-size optimal if it achieves minimum size under given depth requirement depth-size optimal Zero-deficiency 11/27/2020 32

Zero-deficiency/depth-size optimal o The big picture What is the minimum depth of zerodeficiency circuits for a given width? 11/27/2020 33

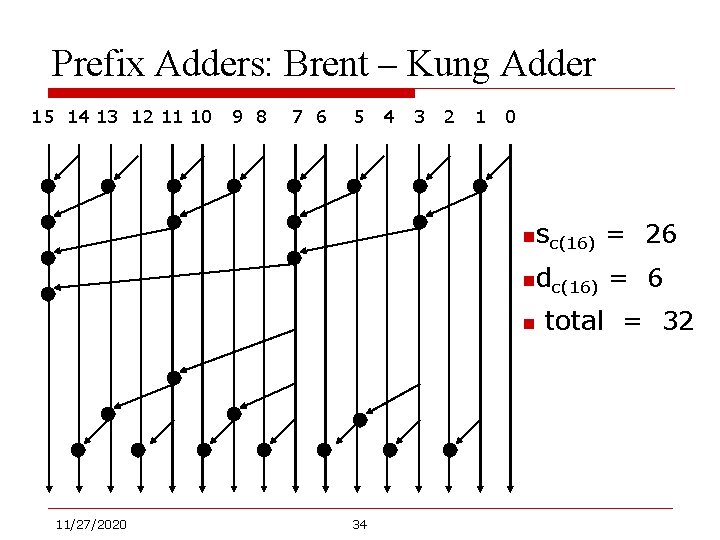
Prefix Adders: Brent – Kung Adder 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 nsc(16) = 26 ndc(16) = 6 n 11/27/2020 34 total = 32