CSE 245 Computer Aided Circuit Simulation and Verification

CSE 245: Computer Aided Circuit Simulation and Verification Nonlinear Equation

Outline o Nonlinear problems o Iterative Methods o Newton’s Method o o n n Derivation of Newton Quadratic Convergence Examples Convergence Testing n n n Basic Algorithm Quadratic convergence Application to circuits n Limiting Schemes o Direction Corrupting o Non corrupting (Damped Newton) Continuation Schemes o Source stepping Multidimensonal Newton Method Improve Convergence n 12 September 2021 2 courtesy Alessandra Nardi UCB

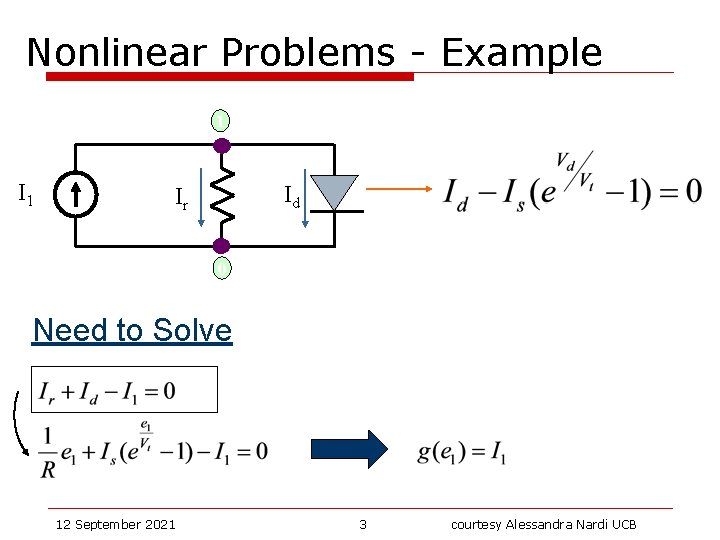
Nonlinear Problems - Example 1 Id Ir 0 Need to Solve 12 September 2021 3 courtesy Alessandra Nardi UCB

Nonlinear Equations o Given g(V)=I o It can be expressed as: f(V)=g(V)-I Solve g(V)=I equivalent to solve f(V)=0 Hard to find analytical solution for f(x)=0 Solve iteratively 12 September 2021 4 courtesy Alessandra Nardi UCB

Nonlinear Equations – Iterative Methods o Start from an initial value x 0 o Generate a sequence of iterate xn-1, xn+1 which hopefully converges to the solution x* o Iterates are generated according to an iteration function F: xn+1=F(xn) Ask • When does it converge to correct solution ? • What is the convergence rate ? 12 September 2021 5 courtesy Alessandra Nardi UCB

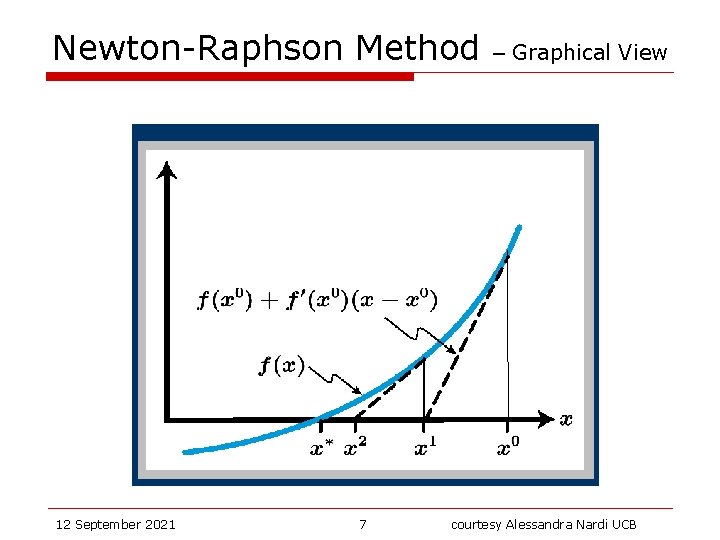
Newton-Raphson (NR) Method Consists of linearizing the system. Want to solve f(x)=0 Replace f(x) with its linearized version and solve. Note: at each step need to evaluate f and f’ 12 September 2021 6 courtesy Alessandra Nardi UCB

Newton-Raphson Method 12 September 2021 7 – Graphical View courtesy Alessandra Nardi UCB

Newton-Raphson Method – Algorithm Define iteration Do k = 0 to …. until convergence o How about convergence? o An iteration {x(k)} is said to converge with order q if there exists a vector norm such that for each k N: 12 September 2021 8 courtesy Alessandra Nardi UCB

Newton-Raphson Method – Convergence Mean Value theorem truncates Taylor series But by Newton definition 12 September 2021 9 courtesy Alessandra Nardi UCB

Newton-Raphson Method – Convergence Subtracting Dividing through Convergence is quadratic 12 September 2021 10 courtesy Alessandra Nardi UCB

Newton-Raphson Method – Convergence Local Convergence Theorem If Then Newton’s method converges given a sufficiently close initial guess (and convergence is quadratic) 12 September 2021 11 courtesy Alessandra Nardi UCB

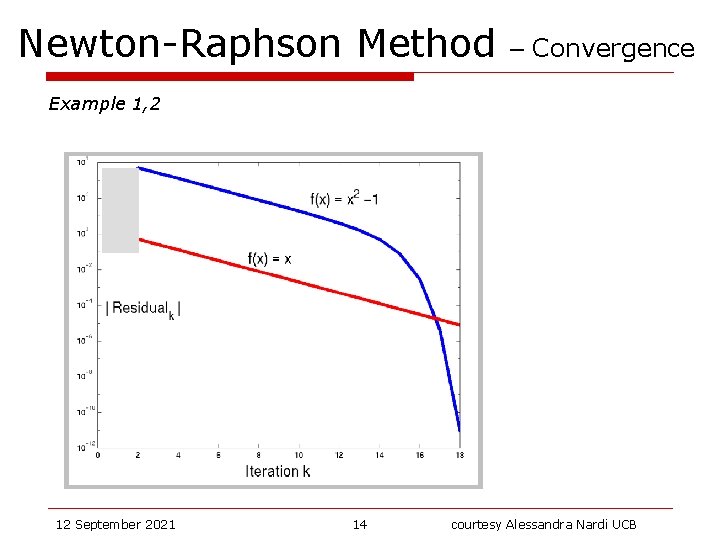
Newton-Raphson Method – Convergence Example 1 Convergence is quadratic 12 September 2021 12 courtesy Alessandra Nardi UCB

Newton-Raphson Method – Convergence Example 2 Note : not bounded away from zero Convergence is linear 12 September 2021 13 courtesy Alessandra Nardi UCB

Newton-Raphson Method – Convergence Example 1, 2 12 September 2021 14 courtesy Alessandra Nardi UCB

Newton-Raphson Method 12 September 2021 15 – Convergence courtesy Alessandra Nardi UCB

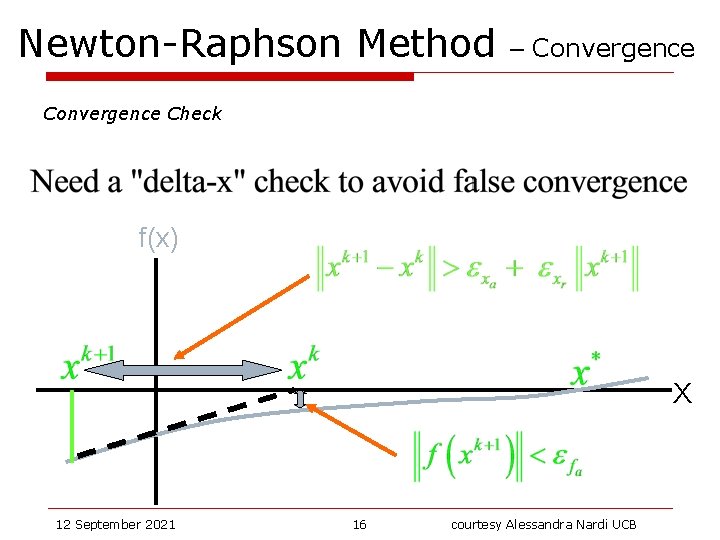
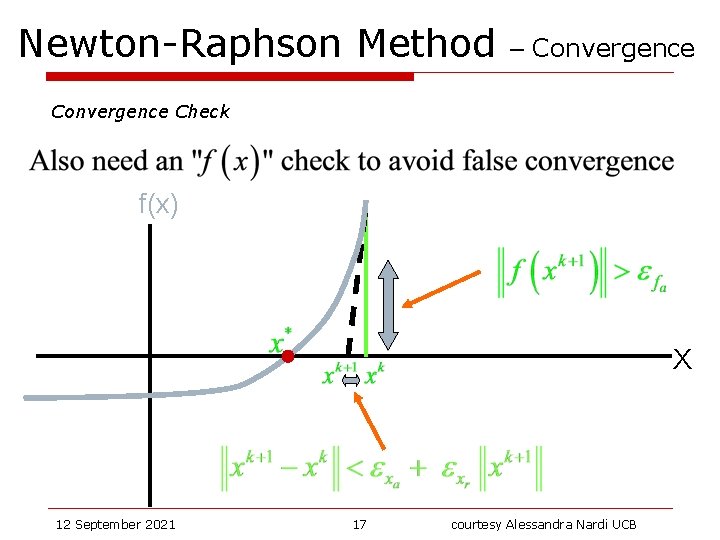
Newton-Raphson Method – Convergence Check f(x) X 12 September 2021 16 courtesy Alessandra Nardi UCB

Newton-Raphson Method – Convergence Check f(x) X 12 September 2021 17 courtesy Alessandra Nardi UCB

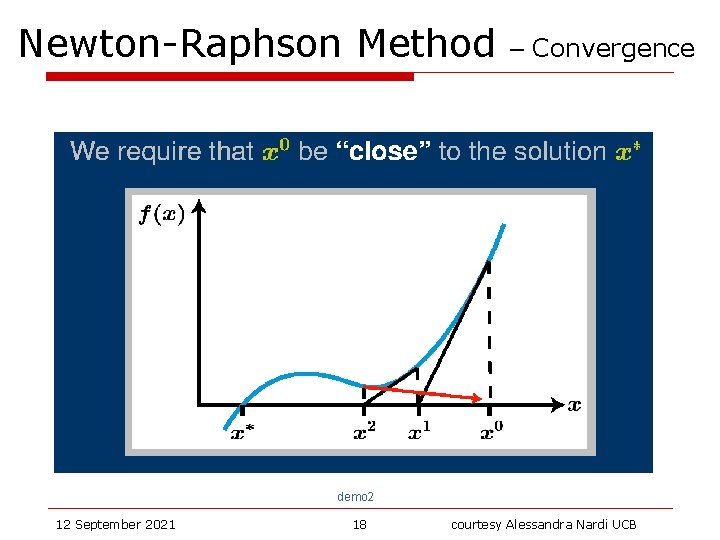
Newton-Raphson Method – Convergence demo 2 12 September 2021 18 courtesy Alessandra Nardi UCB

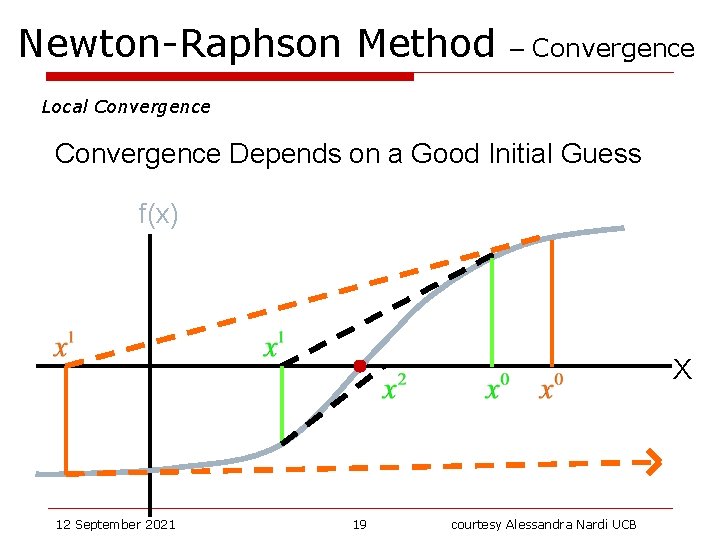
Newton-Raphson Method – Convergence Local Convergence Depends on a Good Initial Guess f(x) X 12 September 2021 19 courtesy Alessandra Nardi UCB

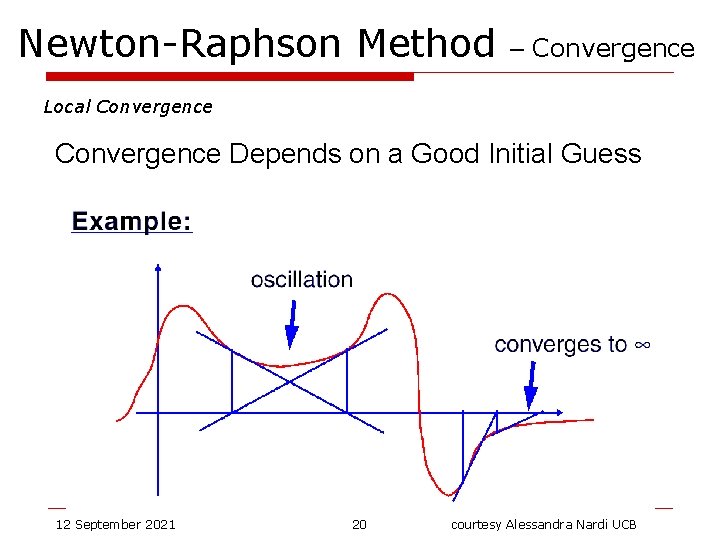
Newton-Raphson Method – Convergence Local Convergence Depends on a Good Initial Guess 12 September 2021 20 courtesy Alessandra Nardi UCB

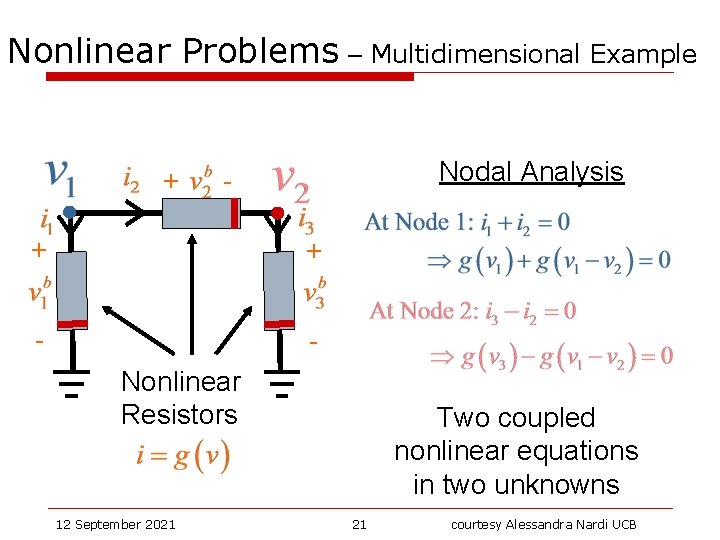
Nonlinear Problems – Multidimensional Example + Nodal Analysis - + + - Nonlinear Resistors 12 September 2021 Two coupled nonlinear equations in two unknowns 21 courtesy Alessandra Nardi UCB

Outline o Nonlinear problems o Iterative Methods o Newton’s Method o o n n Derivation of Newton Quadratic Convergence Examples Convergence Testing n n n Basic Algorithm Quadratic convergence Application to circuits n Limiting Schemes o Direction Corrupting o Non corrupting (Damped Newton) Continuation Schemes o Source stepping Multidimensonal Newton Method Improve Convergence n 12 September 2021 22 courtesy Alessandra Nardi UCB

Multidimensional Newton Method 12 September 2021 23 courtesy Alessandra Nardi UCB

Multidimensional Newton Method Computational Aspects Each iteration requires: 1. Evaluation of F(xk) 2. Computation of J(xk) 3. Solution of a linear system of algebraic equations whose coefficient matrix is J(xk) and whose RHS is -F(xk) 12 September 2021 24 courtesy Alessandra Nardi UCB

Multidimensional Newton Method Algorithm 12 September 2021 25 courtesy Alessandra Nardi UCB

Multidimensional Newton Method Convergence Local Convergence Theorem If Then Newton’s method converges given a sufficiently close initial guess (and convergence is quadratic) 12 September 2021 26 courtesy Alessandra Nardi UCB

Application of NR to Circuit Equations Companion Network o Applying NR to the system of equations we find that at iteration k+1: n all the coefficients of KCL, KVL and of BCE of the linear elements remain unchanged with respect to iteration k n Nonlinear elements are represented by a linearization of BCE around iteration k This system of equations can be interpreted as the STA of a linear circuit (companion network) whose elements are specified by the linearized BCE. 12 September 2021 27 courtesy Alessandra Nardi UCB

Application of NR to Circuit Equations Companion Network o General procedure: the NR method applied to a nonlinear circuit whose eqns are formulated in the STA form produces at each iteration the STA eqns of a linear resistive circuit obtained by linearizing the BCE of the nonlinear elements and leaving all the other BCE unmodified o After the linear circuit is produced, there is no need to stick to STA, but other methods (such as MNA) may be used to assemble the circuit eqns 12 September 2021 28 courtesy Alessandra Nardi UCB

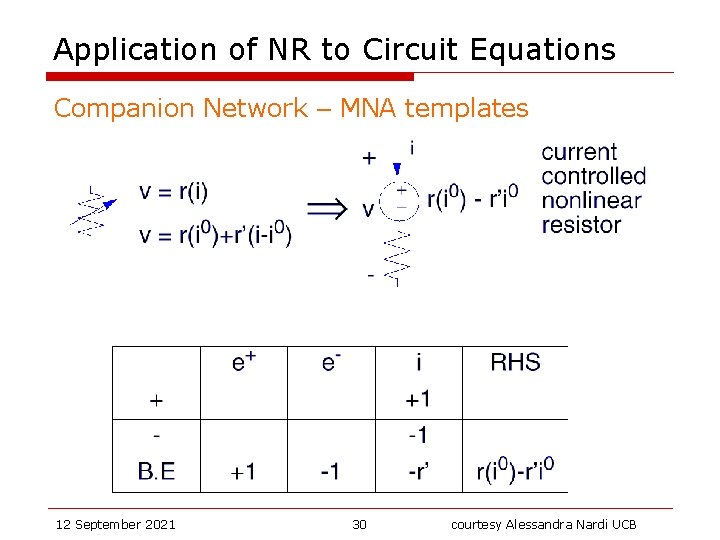
Application of NR to Circuit Equations Companion Network – MNA templates Note: G 0 and Id depend on the iteration count k G 0=G 0(k) and Id=Id(k) 12 September 2021 29 courtesy Alessandra Nardi UCB

Application of NR to Circuit Equations Companion Network – MNA templates 12 September 2021 30 courtesy Alessandra Nardi UCB

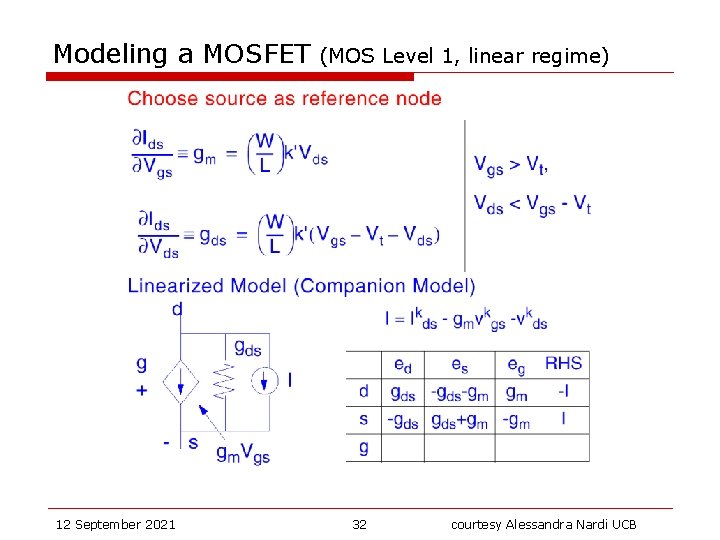
Modeling a MOSFET (MOS Level 1, linear regime) d 12 September 2021 31 courtesy Alessandra Nardi UCB

Modeling a MOSFET 12 September 2021 (MOS Level 1, linear regime) 32 courtesy Alessandra Nardi UCB

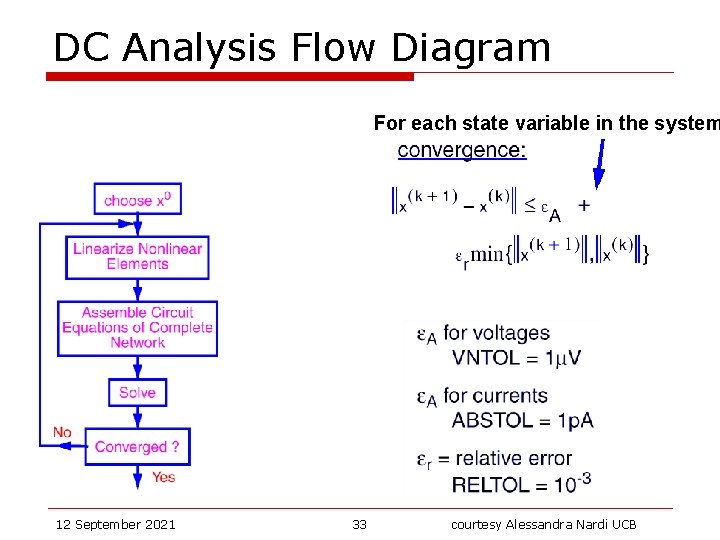
DC Analysis Flow Diagram For each state variable in the system 12 September 2021 33 courtesy Alessandra Nardi UCB

Implications o Device model equations must be continuous with continuous derivatives (not all models do this - - be sure models are decent - beware of user-supplied models) o Watch out for floating nodes (If a node becomes disconnected, then J(x) is singular) o Give good initial guess for x(0) o Most model computations produce errors in function values and derivatives. Want to have convergence criteria || x(k+1) - x(k) || < such that > than model errors. 12 September 2021 34 courtesy Alessandra Nardi UCB

Outline o Nonlinear problems o Iterative Methods o Newton’s Method o o n n Derivation of Newton Quadratic Convergence Examples Convergence Testing n n n Basic Algorithm Quadratic convergence Application to circuits n Limiting Schemes o Direction Corrupting o Non corrupting (Damped Newton) Continuation Schemes o Source stepping Multidimensonal Newton Method Improve Convergence n 12 September 2021 35 courtesy Alessandra Nardi UCB

Improving convergence o Improve Models (80% of problems) o Improve Algorithms (20% of problems) Focus on new algorithms: Limiting Schemes Continuations Schemes 12 September 2021 36 courtesy Alessandra Nardi UCB

Improve Convergence o Limiting Schemes n Direction Corrupting n Non corrupting (Damped Newton) o Globally Convergent if Jacobian is Nonsingular o Difficulty with Singular Jacobians o Continuation Schemes n Source stepping 12 September 2021 37 courtesy Alessandra Nardi UCB

Multidimensional Newton Method Convergence Problems – Local Minimum 12 September 2021 38 courtesy Alessandra Nardi UCB

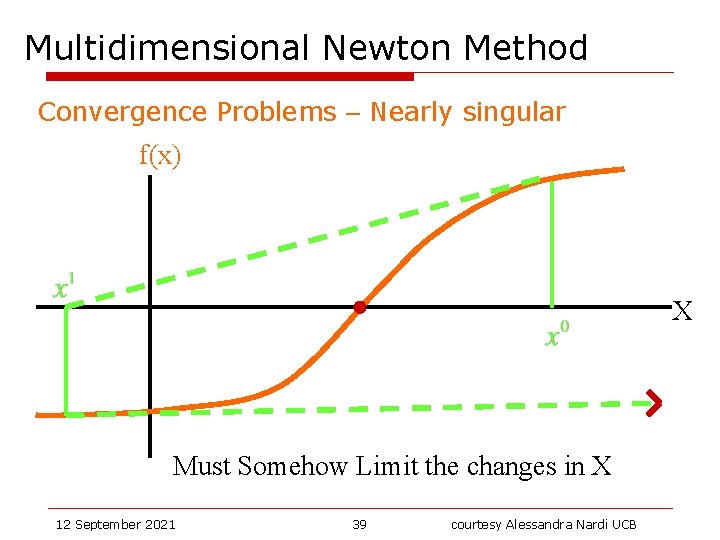
Multidimensional Newton Method Convergence Problems – Nearly singular f(x) X Must Somehow Limit the changes in X 12 September 2021 39 courtesy Alessandra Nardi UCB

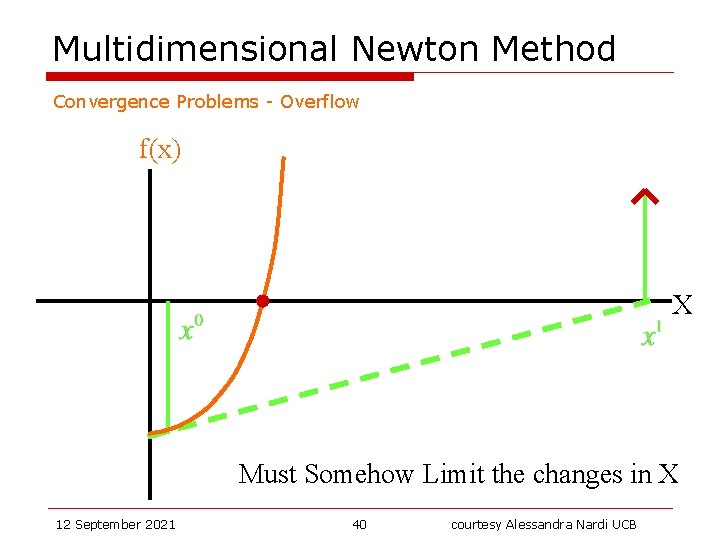
Multidimensional Newton Method Convergence Problems - Overflow f(x) X Must Somehow Limit the changes in X 12 September 2021 40 courtesy Alessandra Nardi UCB

Newton Method with Limiting 12 September 2021 41 courtesy Alessandra Nardi UCB

Newton Method with Limiting Methods • Direction Corrupting • Non. Corrupting Heuristics, No Guarantee of Global Convergence 12 September 2021 42 courtesy Alessandra Nardi UCB

Newton Method with Limiting Damped Newton Scheme General Damping Scheme Key Idea: Line Search Method Performs a one-dimensional search in Newton Direction 12 September 2021 43 courtesy Alessandra Nardi UCB

Newton Method with Limiting Damped Newton – Convergence Theorem If Then Every Step reduces F-- Global Convergence! 12 September 2021 44 courtesy Alessandra Nardi UCB

Newton Method with Limiting Damped Newton – Nested Iteration 12 September 2021 45 courtesy Alessandra Nardi UCB

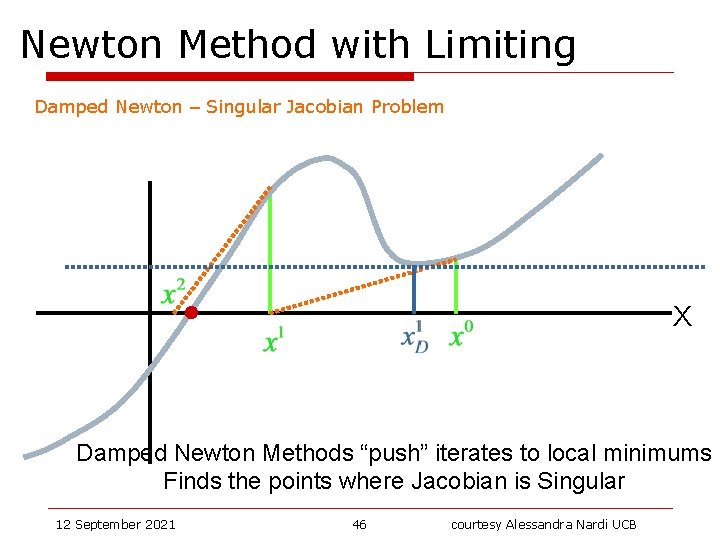
Newton Method with Limiting Damped Newton – Singular Jacobian Problem X Damped Newton Methods “push” iterates to local minimums Finds the points where Jacobian is Singular 12 September 2021 46 courtesy Alessandra Nardi UCB

Newton with Continuation schemes Basic Concepts - General setting Newton converges given a close initial guess Idea: Generate a sequence of problems, s. t. a problem is a good initial guess for the following one Starts the continuation Ends the continuation Hard to insure! 12 September 2021 47 courtesy Alessandra Nardi UCB

Newton with Continuation schemes Basic Concepts – Template Algorithm 12 September 2021 48 courtesy Alessandra Nardi UCB

Newton with Continuation schemes Basic Concepts – Source Stepping Example 12 September 2021 49 courtesy Alessandra Nardi UCB

Newton with Continuation schemes Basic Concepts – Source Stepping Example R Vs Diode + - Source Stepping Does Not Alter Jacobian 12 September 2021 50 courtesy Alessandra Nardi UCB

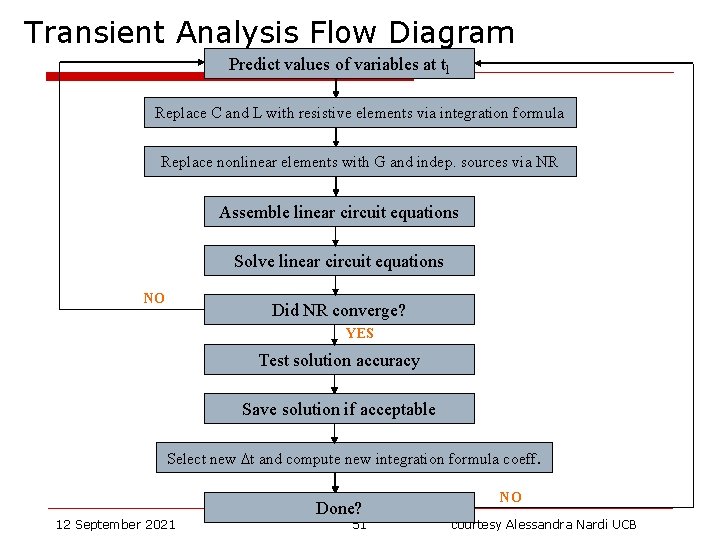
Transient Analysis Flow Diagram Predict values of variables at tl Replace C and L with resistive elements via integration formula Replace nonlinear elements with G and indep. sources via NR Assemble linear circuit equations Solve linear circuit equations NO Did NR converge? YES Test solution accuracy Save solution if acceptable Select new Dt and compute new integration formula coeff. 12 September 2021 Done? 51 NO courtesy Alessandra Nardi UCB