CSE 245 Computer Aided Circuit Simulation and Verification

CSE 245: Computer Aided Circuit Simulation and Verification Winter 2003 Lecture 1: Formulation Instructor: Prof. Chung-Kuan Cheng Jan. 24, 2003 Cheng & Zhu, UCSD @ 2003

Agenda o o o RCL Network Sparse Tableau Analysis Modified Nodal Analysis Jan. 24, 2003 2 Cheng & Zhu, UCSD @ 2003

History of SPICE o o o o SPICE -- Simulation Program with Integrated Circuit Emphasis 1969, CANCER developed by Laurence Nagel on Prof. Ron Roher’s class 1970~1972, CANCER program May 1972, SPICE-I release July ’ 75, SPICE 2 A, …, 2 G Aug 1982, SPICE 3 (in C language) No new progress on software package since then Jan. 24, 2003 3 Cheng & Zhu, UCSD @ 2003

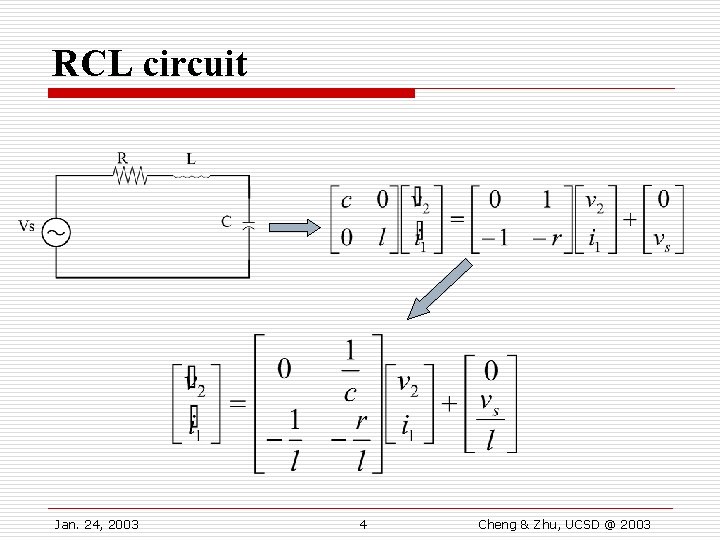
RCL circuit Jan. 24, 2003 4 Cheng & Zhu, UCSD @ 2003

RCL circuit (II) o General Circuit Equation o Consider homogeneous form first and Q: How to Compute Ak ? Jan. 24, 2003 5 Cheng & Zhu, UCSD @ 2003

Solving RCL Equation o Assume A has non-degenerate eigenvalues and corresponding linearly independent eigenvectors , then A can be decomposed as where Jan. 24, 2003 and 6 Cheng & Zhu, UCSD @ 2003

Solving RCL Equation (II) o What’s the implication then? where o To compute the eigenvalues: real eigenvalue Jan. 24, 2003 Conjugative Complex eigenvalue 7 Cheng & Zhu, UCSD @ 2003

Solving RCL Equation (III) In the previous example Let c=r=l=1, we have where hence Jan. 24, 2003 8 Cheng & Zhu, UCSD @ 2003

Solving RCL Equation (IV) o What if matrix A has degenerated eigenvalues? Jordan decomposition ! J is in the Jordan Canonical form And still Jan. 24, 2003 9 Cheng & Zhu, UCSD @ 2003

Jordan Decomposition similarly Jan. 24, 2003 10 Cheng & Zhu, UCSD @ 2003

Agenda o o o RCL Network Sparse Tableau Analysis Modified Nodal Analysis Jan. 24, 2003 11 Cheng & Zhu, UCSD @ 2003

Equation Formulation o KCL n o KVL n o Converge of node current Closure of loop voltage Brach equations n I, R relations Jan. 24, 2003 12 Cheng & Zhu, UCSD @ 2003

Types of elements o Resistor Capacitor o Inductor o n o L is even dependent on frequency due to skin effect, etc… Controlled Sources n VCVS, VCCS, CCVS, CCCS Jan. 24, 2003 13 Cheng & Zhu, UCSD @ 2003

Cut-set analysis 1. Construct a spanning tree 2. Take as much capacitor branches as tree branches as possible 3. Derive the fundamental cut-set, in which each cut truncates exactly one tree branch 4. Write KCL equations for each cut 5. Write KVL equations for each tree link 6. Write the constitution equation for each branch Jan. 24, 2003 14 Cheng & Zhu, UCSD @ 2003

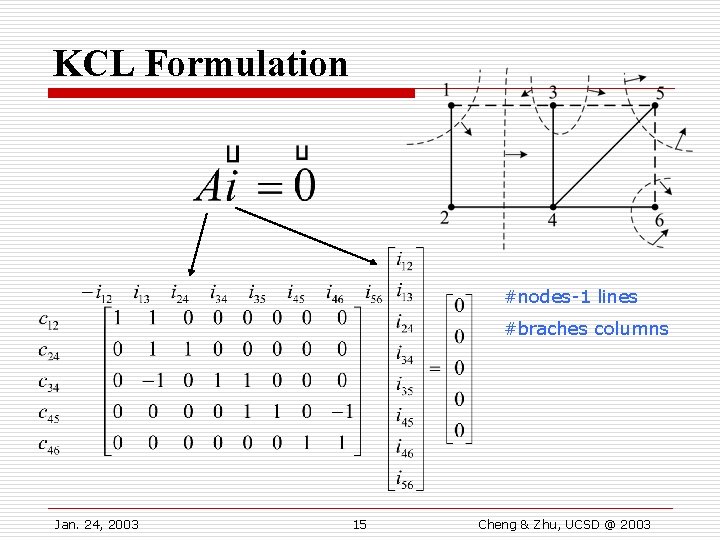
KCL Formulation #nodes-1 lines #braches columns Jan. 24, 2003 15 Cheng & Zhu, UCSD @ 2003

KCL Formulation (II) o Permute the columns to achieve a systematic form Jan. 24, 2003 16 Cheng & Zhu, UCSD @ 2003

KVL Formulation Remove the equations for tree braches and systemize Jan. 24, 2003 17 Cheng & Zhu, UCSD @ 2003

Cut & Loop relation In the previous example Jan. 24, 2003 18 Cheng & Zhu, UCSD @ 2003

Sparse Tableau Analysis (STA) o n=#nodes, b=#branches b b n-1 (n-1) KCL b b b KVL b branch relations n-1 Due to independent sources Totally 2 b+n-1 variables, 2 b+n-1 equations Jan. 24, 2003 19 Cheng & Zhu, UCSD @ 2003

STA (II) o Advantages n n n Covers any circuit Easy to assemble Very sparse o o Ki, Kv, I each has exactly b non-zeros. A and AT each has at most 2 b non-zeros. Disadvantages n Sophisticated data structures & programming techniques Jan. 24, 2003 20 Cheng & Zhu, UCSD @ 2003

Agenda o o o RCL Network Sparse Tableau Analysis Modified Nodal Analysis Jan. 24, 2003 21 Cheng & Zhu, UCSD @ 2003

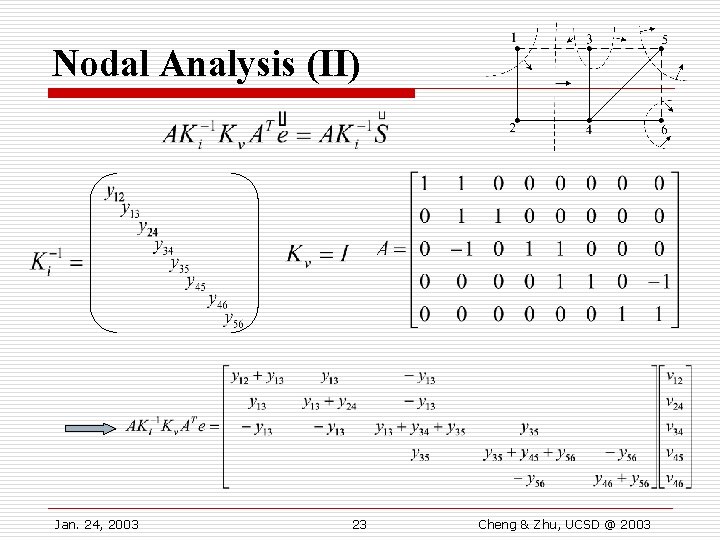
Nodal Analysis o Derivation (1) From STA: (2) (3) x Ki-1 (4) x A (5) Using (a) (6) Tree trunk voltages Substitute with node voltages (to a given reference), we get the nodal analysis equations. Jan. 24, 2003 22 Cheng & Zhu, UCSD @ 2003

Nodal Analysis (II) Jan. 24, 2003 23 Cheng & Zhu, UCSD @ 2003

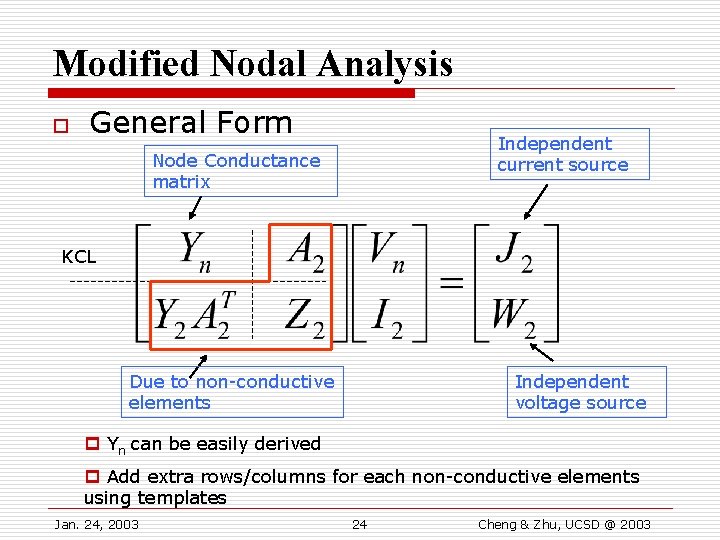
Modified Nodal Analysis o General Form Independent current source Node Conductance matrix KCL Due to non-conductive elements Independent voltage source p Yn can be easily derived p Add extra rows/columns for each non-conductive elements using templates Jan. 24, 2003 24 Cheng & Zhu, UCSD @ 2003

MNA (II) o Fill Yn matrix according to incidence matrix Choose n 6 as reference node Jan. 24, 2003 25 Cheng & Zhu, UCSD @ 2003

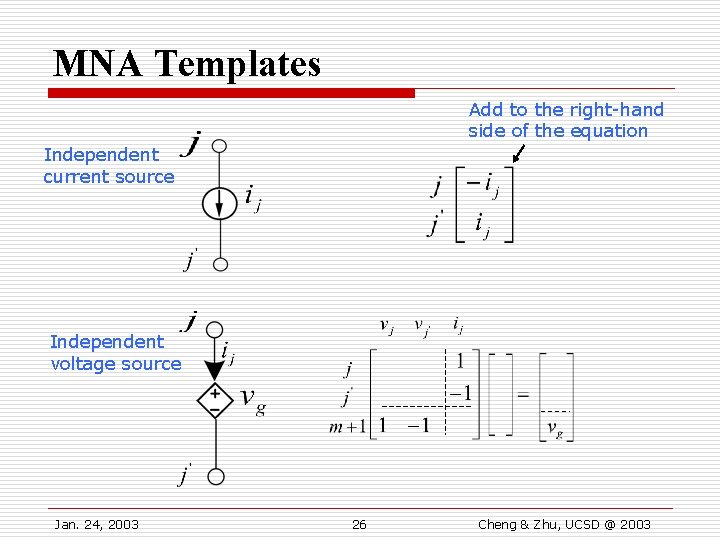
MNA Templates Add to the right-hand side of the equation Independent current source Independent voltage source Jan. 24, 2003 26 Cheng & Zhu, UCSD @ 2003

MNA Templates (II) CCVS CCCS Jan. 24, 2003 27 Cheng & Zhu, UCSD @ 2003

MNA Templates (III) VCVS + - VCCS + - Jan. 24, 2003 28 Cheng & Zhu, UCSD @ 2003

MNA Templates (IV) Mutual inductance M Operational Amplifier Jan. 24, 2003 29 Cheng & Zhu, UCSD @ 2003

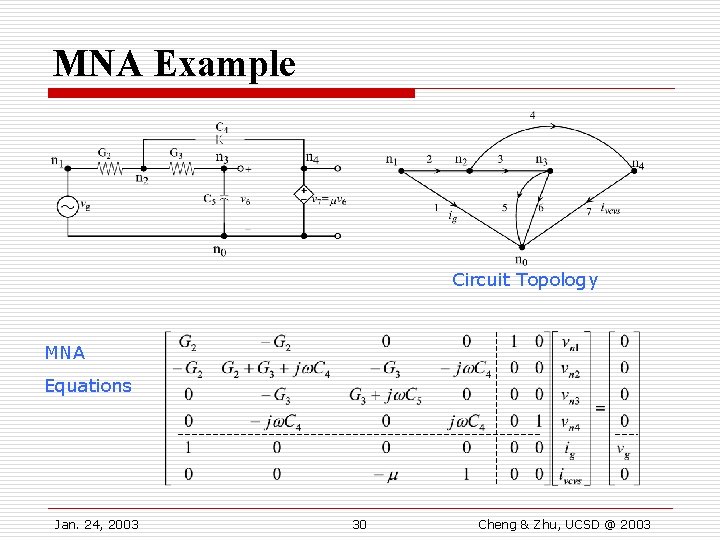
MNA Example Circuit Topology MNA Equations Jan. 24, 2003 30 Cheng & Zhu, UCSD @ 2003

MNA Summary o Advantages n n o Covers any circuits Can be assembled directly from input data. Matrix form is close to Yn Disadvantages n n We may have zeros on the main diagonal. Principle minors could be singular Jan. 24, 2003 31 Cheng & Zhu, UCSD @ 2003