CSE 23315331 Topic 5 Heap data structure heap

CSE 2331/5331 Topic 5: Heap data structure heap sort Priority queue CSE 2331/5331

Sorting Revisited n Insertion sort n n quadratic, but in-place sorting Merge sort n nlg n, but not in-place Heapsort combines best of two CSE 2331/5331

Heap Introduction n n An array A that can be viewed as a nearly complete binary tree An array A representing a heap: n n length(A): size of the array heap-size(A) (≤ length(A)): n Only A[1, …, heap-size(A)] contain elements of the heap. CSE 2331/5331

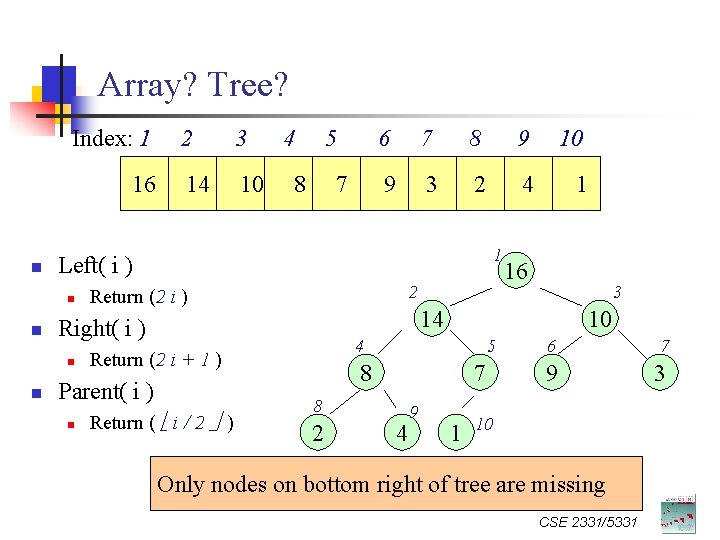
Array? Tree? Index: 1 16 n 14 10 4 5 8 7 6 7 8 9 10 9 3 2 4 1 1 2 Return (2 i ) n Return ( i / 2 ) 3 10 4 Return (2 i + 1 ) Parent( i ) 16 14 Right( i ) n n 3 Left( i ) n n 2 5 8 7 8 2 4 9 1 6 7 9 3 10 Only nodes on bottom right of tree are missing CSE 2331/5331

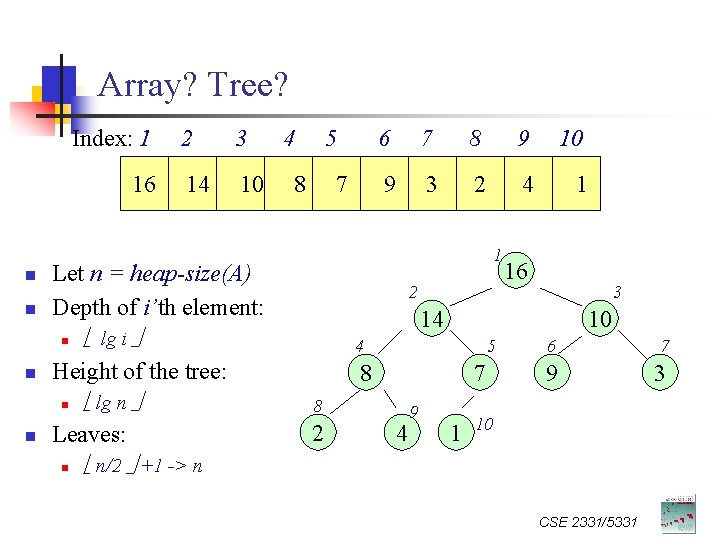
Array? Tree? Index: 1 16 n n 14 10 4 5 8 7 6 7 8 9 10 9 3 2 4 1 1 2 lg i lg n Leaves: n 16 3 14 10 4 Height of the tree: n n 3 Let n = heap-size(A) Depth of i’th element: n n 2 5 8 7 8 2 4 9 1 6 7 9 3 10 n/2 +1 -> n CSE 2331/5331

Max-heap n (Max-)heap property: n A [ Parent( i ) ] ≥ A[ i ] 16 14 10 8 2 7 4 1 9 3 1 CSE 2331/5331

Max-heap n (Max-)heap property: n A [ Parent( i ) ] ≥ A[ i ] 16 14 10 For 8 any node 7 i, A[i]9 is the 3 maximum among all the 2 values 4 in the 1 subtree 1 rooted at i. CSE 2331/5331

Max-heap n (Max-)heap property: n A [ Parent( i ) ] ≥ A[ i ] 16 14 10 8 2 7 4 9 3 1 CSE 2331/5331

Heap Operations n Max-Heapify n Build-Max. Heap n Heap. Sort CSE 2331/5331

Max-Heapify n Input: n n n For a node i, left and right subtrees of i are max-heaps A[i] may be smaller than its children (violates maxheap property) Output: n The subtree rooted at i is a max-heap. Crucial in maintain heap property CSE 2331/5331

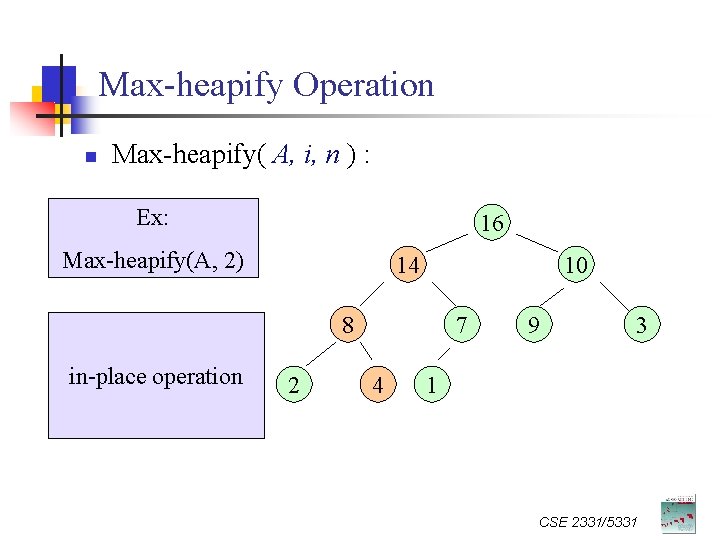
Max-heapify Operation n Max-heapify( A, i, n ) : Ex: 16 Max-heapify(A, 2) 14 4 10 84 14 in-place operation 2 7 48 9 3 1 CSE 2331/5331

Pseudo-code Writing recurrence is not always the best approach. Running time: O(height of i) = O(lg n) CSE 2331/5331

An Non-recursive Algorithm CSE 2331/5331

Build Max-heap Operation n leaves from Build-Max-Heap( A, n ) n/2 to n n = length ( A ); for i = n / 2 downto 1 do Still in-place ! Max-Heapify ( A, i, n ) CSE 2331/5331

Heapsort n n n Input array: A[1. . n] Wish to be in-place sorting First: build heap 16 14 1 A[ 1. . n ] 14 8 A[ A[ 11. . n-1 ]] A[ 1. . n-2 ] 10 48 2 7 14 14 9 3 16 1 CSE 2331/5331

n Heapsort (A, n) Built-Max-Heap (A, n) for i=n downto 2 Exchange A[1] with A[i] Max-Heapify (A, 1, i-1) n Time complexity: n O(n lg n) CSE 2331/5331

Priority Queue n Operations: n n n Init( S ) Insert ( S, key ) Maximum ( S ) Extract-Max ( S ) Increase-key ( S, i, key ) A priority queue can be implemented using various data structures, heap is one of them. CSE 2331/5331

Using Linked List for Priority Queue n Operations: n n n Init( S ) Insert ( S, key ) Maximum ( S ) Extract-Max ( S ) Increase-key ( S, i, key ) O(1) O( sizeof(S) ) O(1) CSE 2331/5331

Heap Implementations n n Maximum ( S ) -- trivially O(1) Extract-Max: Time complexity: O( lg n ) 16 1 CSE 2331/5331

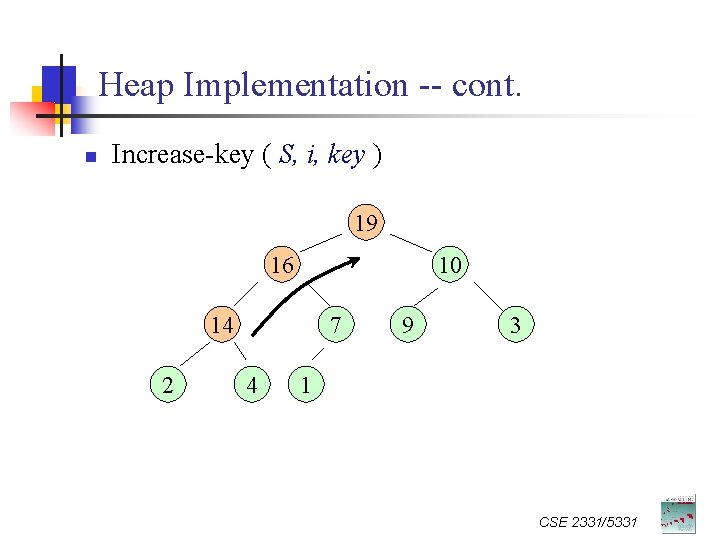
Heap Implementation -- cont. n Increase-key ( S, i, key ) 16 19 14 19 16 10 8 14 19 2 7 4 9 3 1 CSE 2331/5331

Increase-Key n Time complexity: O( lg n) CSE 2331/5331

Increase-Key How about Decrease-key ( S, i, key ) n Time complexity: O( lg n) CSE 2331/5331

Heap Implementation -- cont. Time complexity: O ( lg n ) CSE 2331/5331

Priority Queue – Heap Implementation n Operations: n n Insert ( S, key ) Maximum ( S ) Extract-Max ( S ) Increase-key ( S, i, key ) O(lg n) O(1) O(lg n) A different way to build heap: Insertion-Build-Heap CSE 2331/5331

Another Heap-sort n Time complexity: O(n lg n) CSE 2331/5331

Example of Alg. Analysis n Analyze the running time of the following algorithm, where the priority P is implemented by a Max-heap. CSE 2331/5331

Another Example n Analyze the running time of the following algorithm, where the priority P is implemented by a Max-heap CSE 2331/5331

Summary n Heap n n n Data structure Heapsort Priority queue n Implemented by heap CSE 2331/5331

Lower Bound for Sorting n Model n n What types of operations are allowed E. g: partial sum n n n Both addition and subtraction Addition-only model For sorting: n Comparison-based model CSE 2331/5331

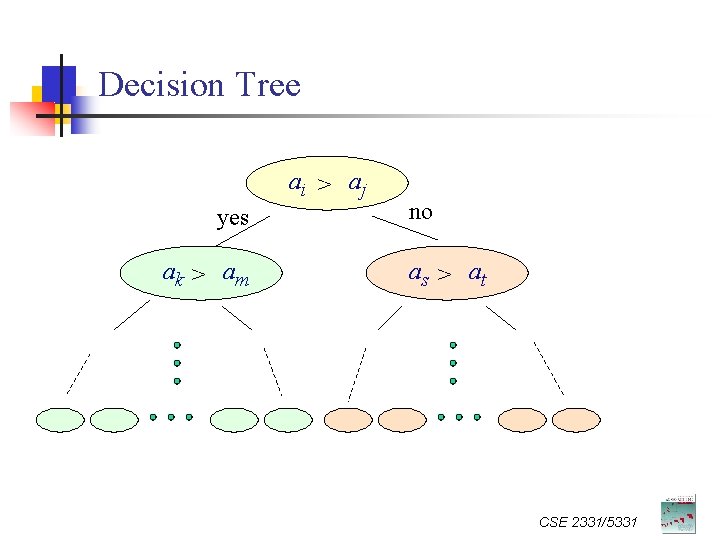
Decision Tree ai > aj yes ak > am no as > at CSE 2331/5331

Example n For insertion sort with 3 elements CSE 2331/5331

Decision Tree n n Not necessary same height Worst case complexity: n n Longest root-leaf path Each leaf: n A possible outcome n n n I. e. , a permutation of input Every possible outcome should be some leaf #leaves ≥ n! CSE 2331/5331

Lower Bound n CSE 2331/5331

Non-comparison Based Sorting n CSE 2331/5331