CSE 23315331 Topic 12 Max Flow Definitions Augmenting

CSE 2331/5331 Topic 12: Max Flow Definitions Augmenting path Max flow min cut CSE 2331/5331

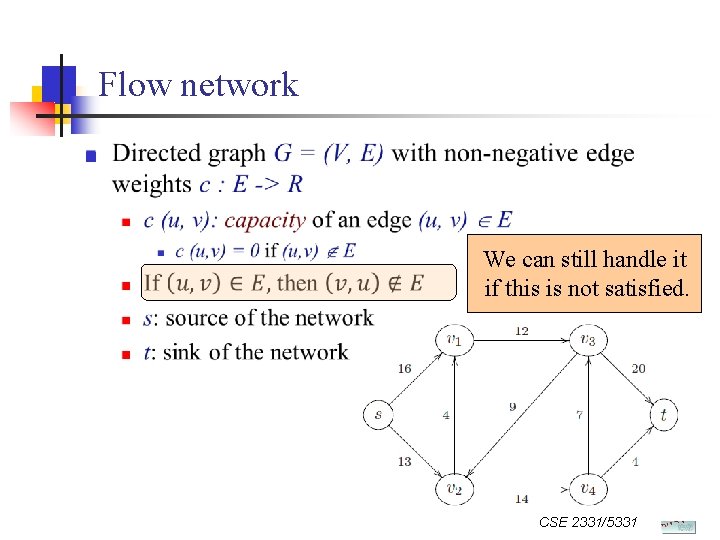
Flow network n We can still handle it if this is not satisfied. CSE 2331/5331

Flow n That is, flow in = flow out. CSE 2331/5331

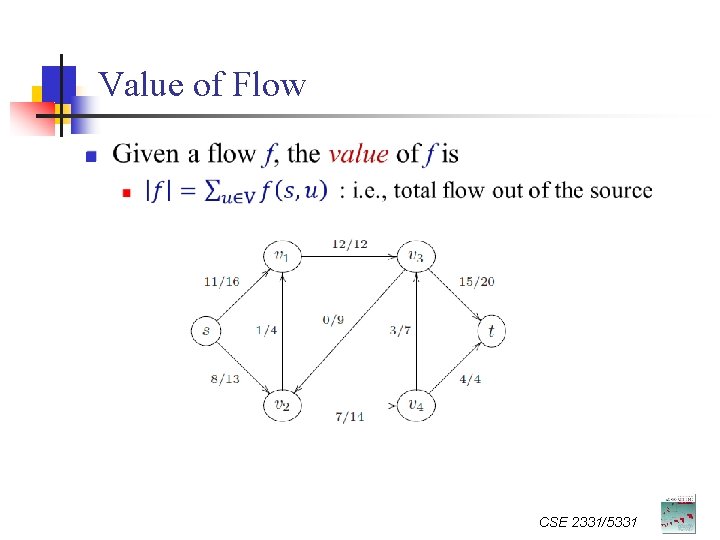
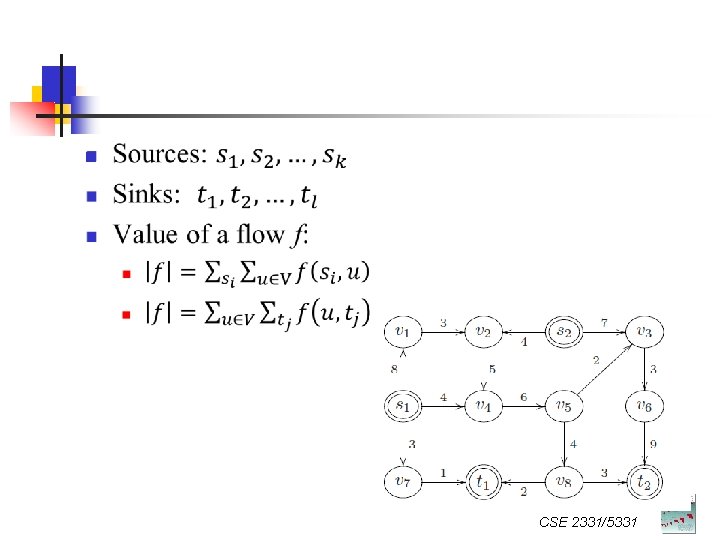
Value of Flow n CSE 2331/5331

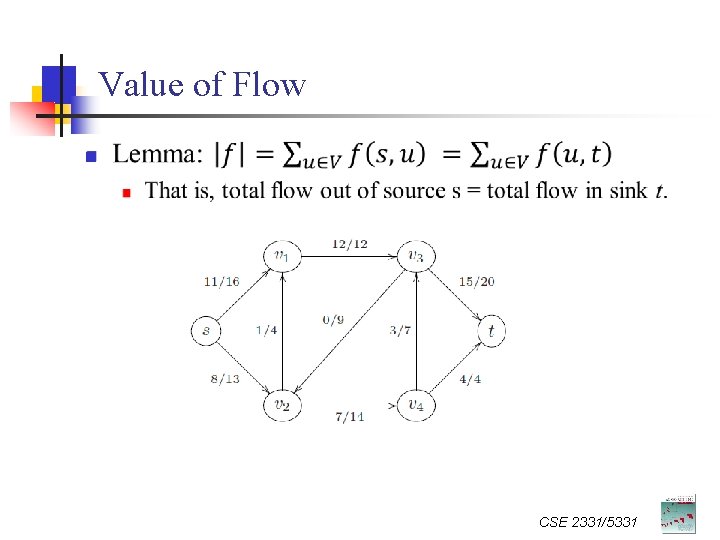
Value of Flow n CSE 2331/5331

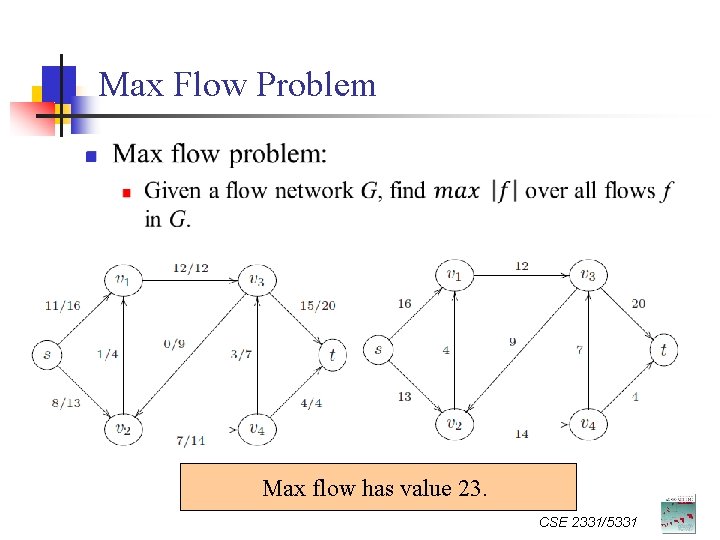
Max Flow Problem n Max flow has value 23. CSE 2331/5331

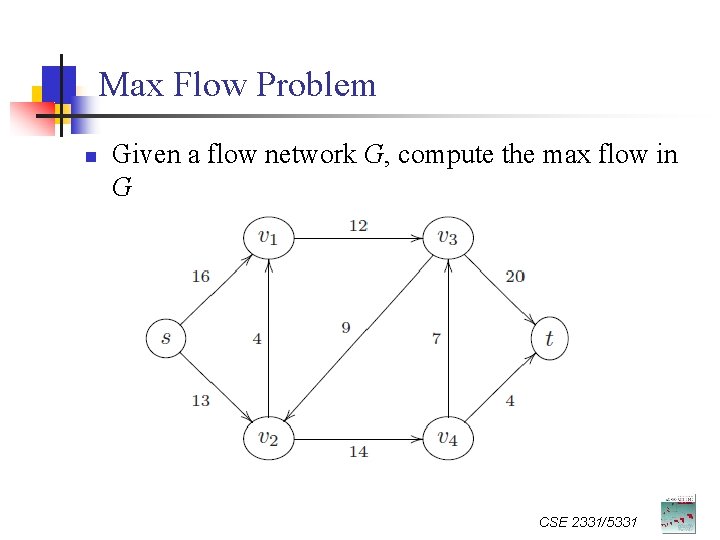
Max Flow Problem n Given a flow network G, compute the max flow in G. CSE 2331/5331

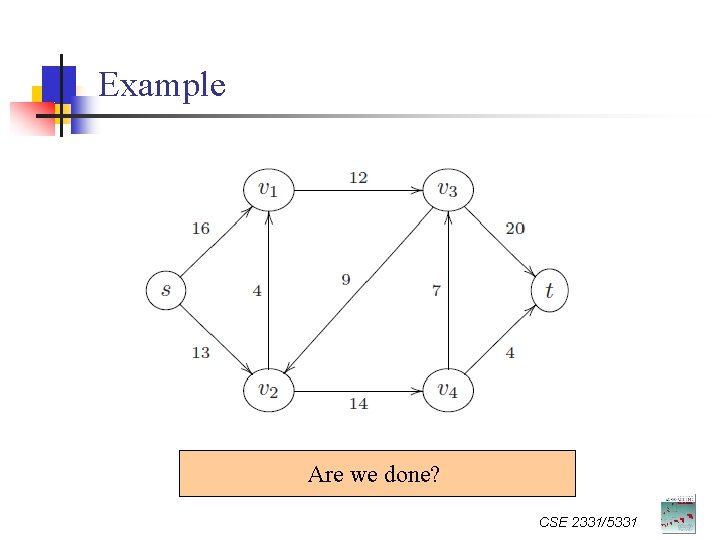
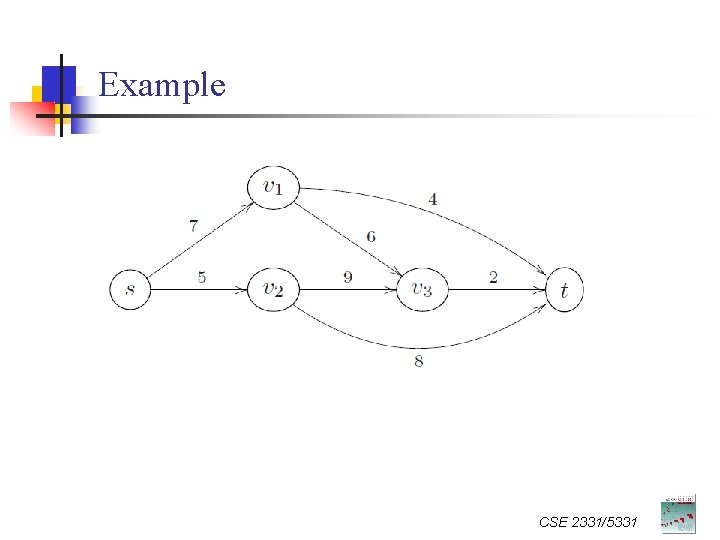
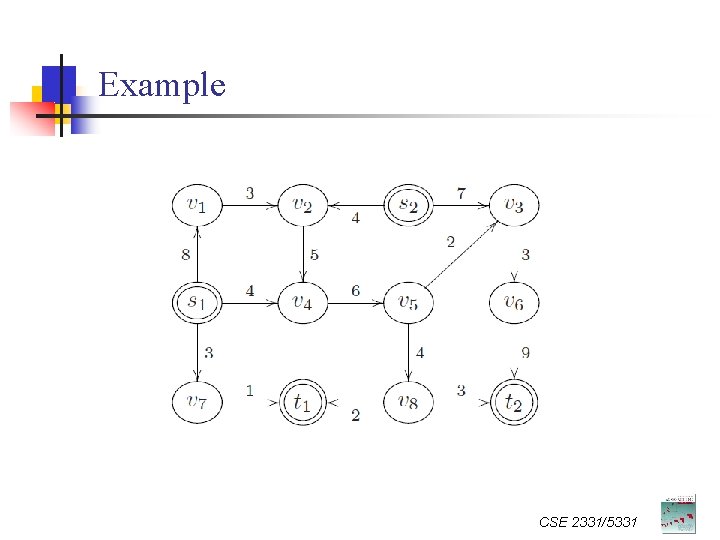
Example Are we done? CSE 2331/5331

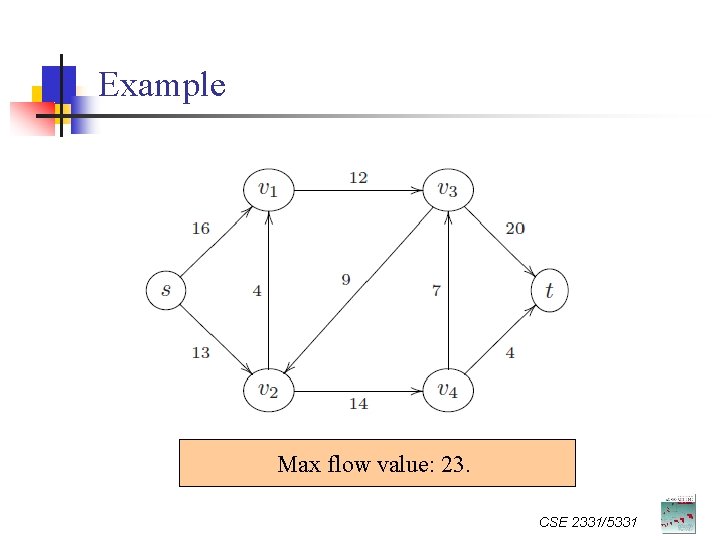
Example Max flow value: 23. CSE 2331/5331

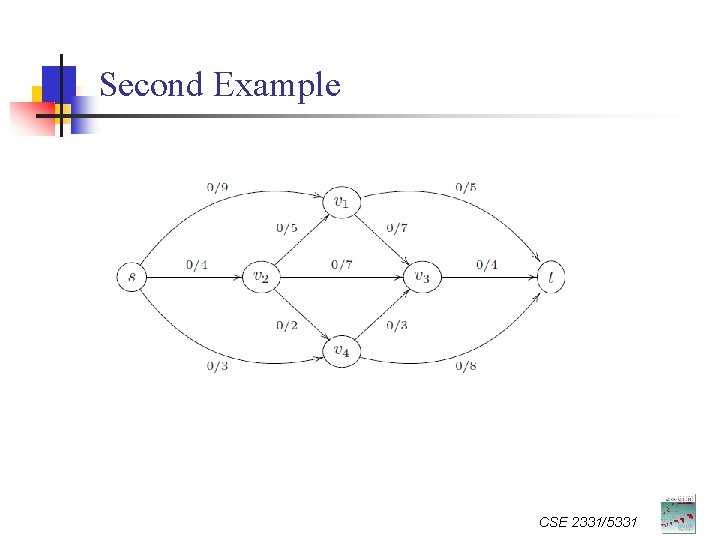
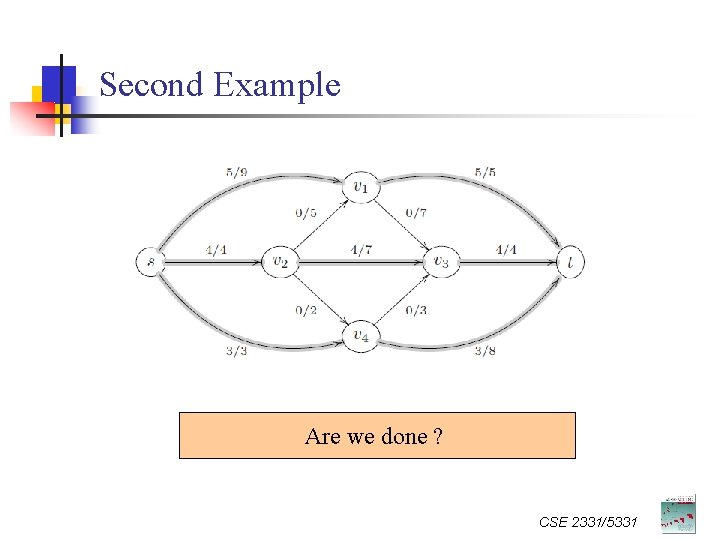
Second Example CSE 2331/5331

Second Example Are we done ? CSE 2331/5331

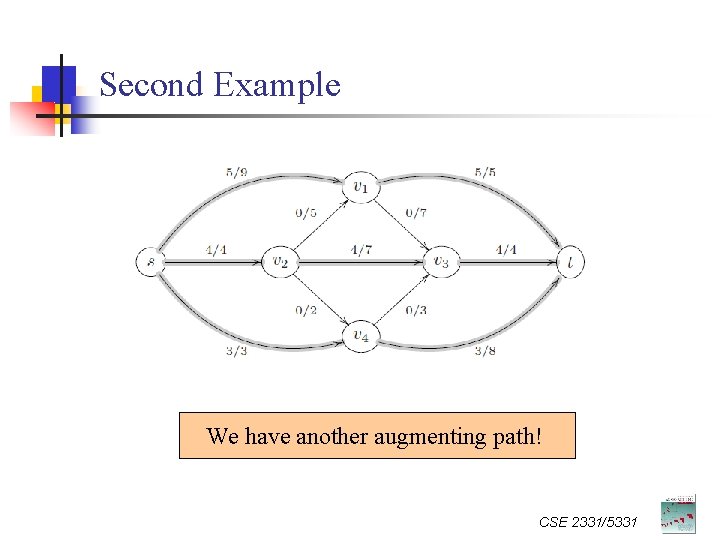
Second Example We have another augmenting path! CSE 2331/5331

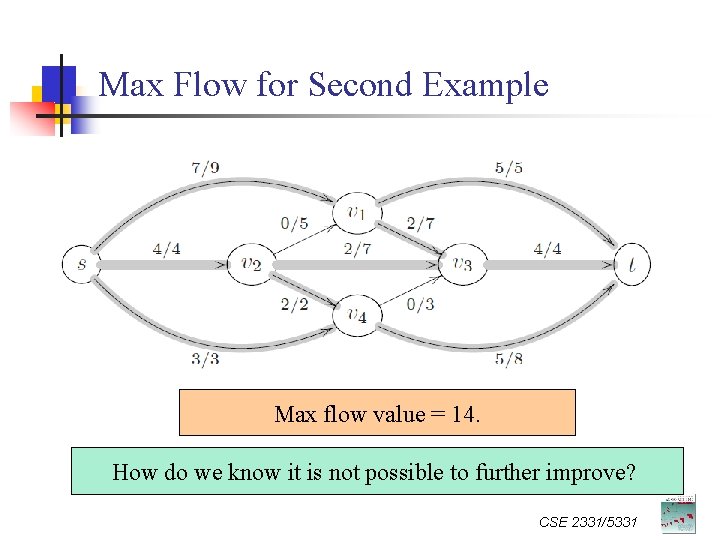
Max Flow for Second Example Max flow value = 14. How do we know it is not possible to further improve? CSE 2331/5331

Residual Network n CSE 2331/5331

Residual Capacity n CSE 2331/5331

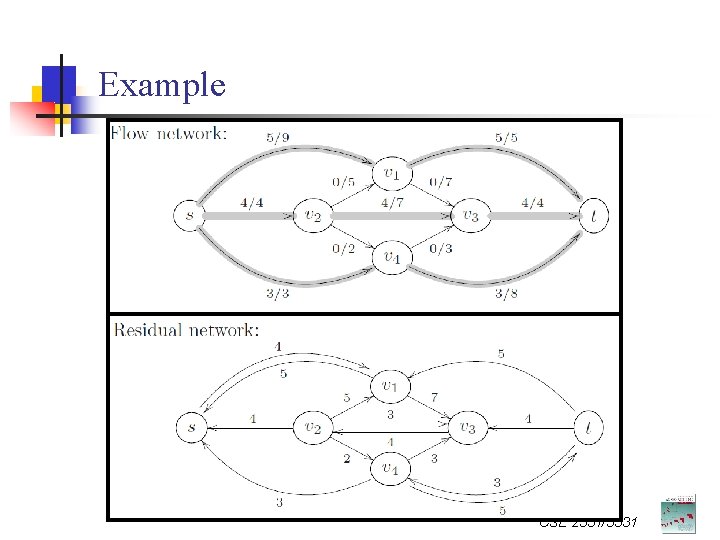
Example CSE 2331/5331

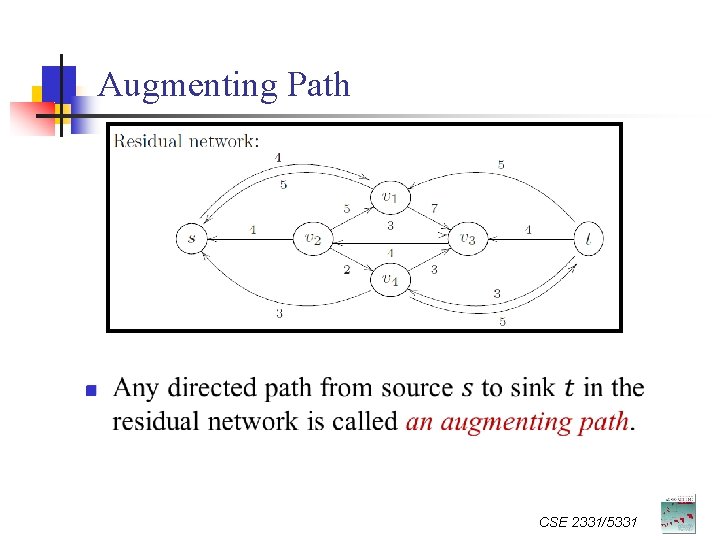
Augmenting Path n CSE 2331/5331

n CSE 2331/5331

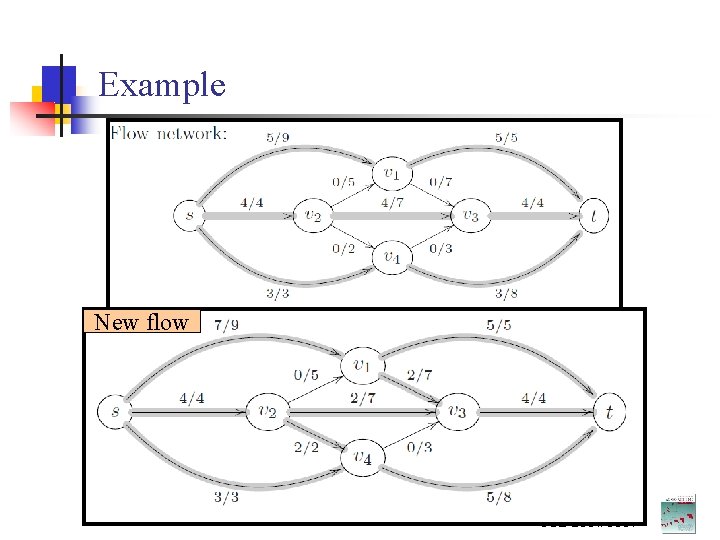
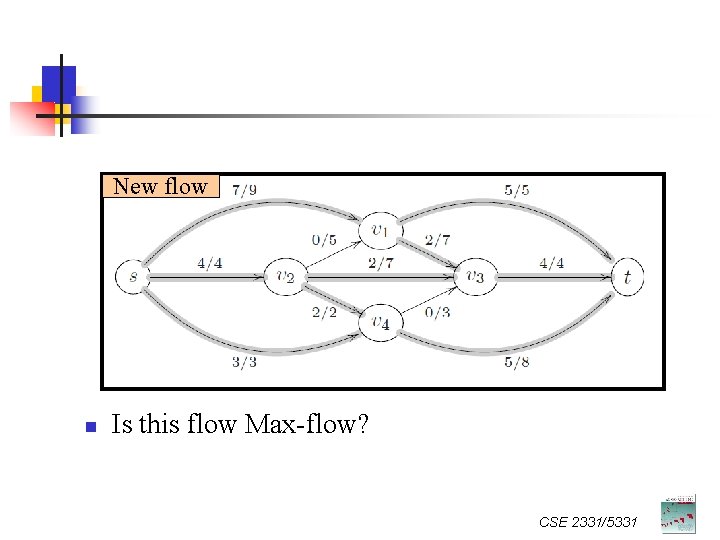
Example New flow CSE 2331/5331

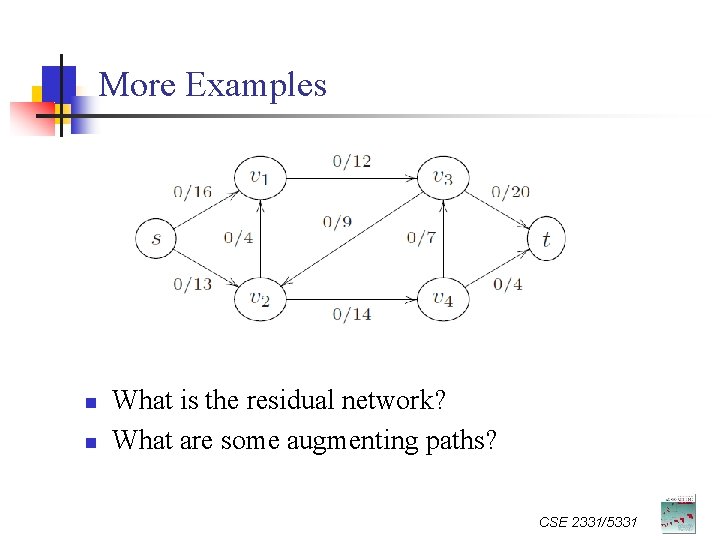
More Examples n n What is the residual network? What are some augmenting paths? CSE 2331/5331

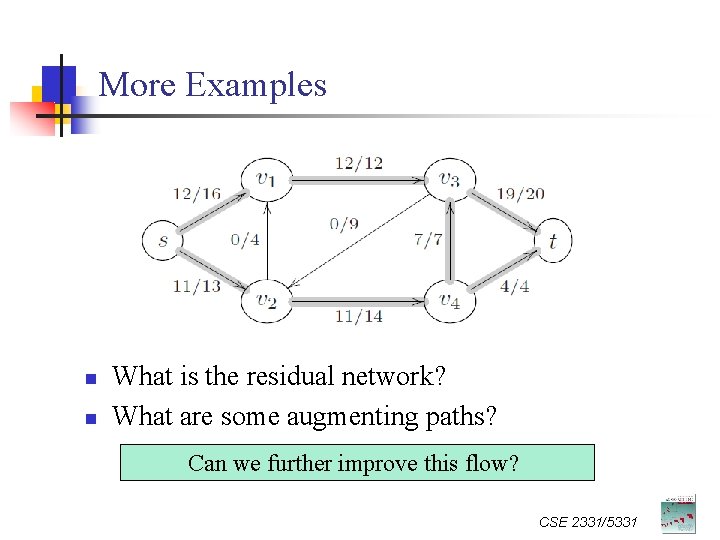
More Examples n n What is the residual network? What are some augmenting paths? Can we further improve this flow? CSE 2331/5331

Max-Flow-Residual Theorem n n Proof: n n One direction easy: If f is max flow, then there is no augmenting path in the residual network. The other direction will be handled later. Suggests an algorithm to compute Max-flow. CSE 2331/5331

New flow n Is this flow Max-flow? CSE 2331/5331

Ford-Fulkerson Max Flow Alg. CSE 2331/5331

Ford-Fulkerson Alg. (More detailed) CSE 2331/5331

Example CSE 2331/5331

Time Complexity Analysis of Ford-Fulkerson Max Flow Algorithm. CSE 2331/5331

CSE 2331/5331

Special Case n Consider only the case where all capacities are integers! CSE 2331/5331

Time Complexity for Integers Case n CSE 2331/5331

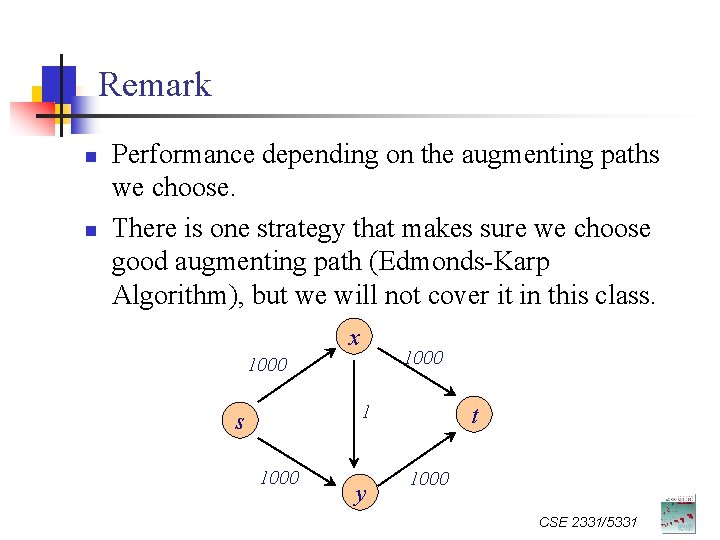
Remark n n Performance depending on the augmenting paths we choose. There is one strategy that makes sure we choose good augmenting path (Edmonds-Karp Algorithm), but we will not cover it in this class. x 1000 1 s 1000 y t 1000 CSE 2331/5331

Multi-sources and multi-sinks flow networks CSE 2331/5331

n CSE 2331/5331

Multi-Source/Sink Max Flow Problem n n Given a flow network with multiple sources and sinks, find the flow with maximum value. Reduce to single source/sink max-flow problem! n By adding an extra super-source and super-sink. CSE 2331/5331

Example CSE 2331/5331

Multi-Source/Sink Max-Flow CSE 2331/5331

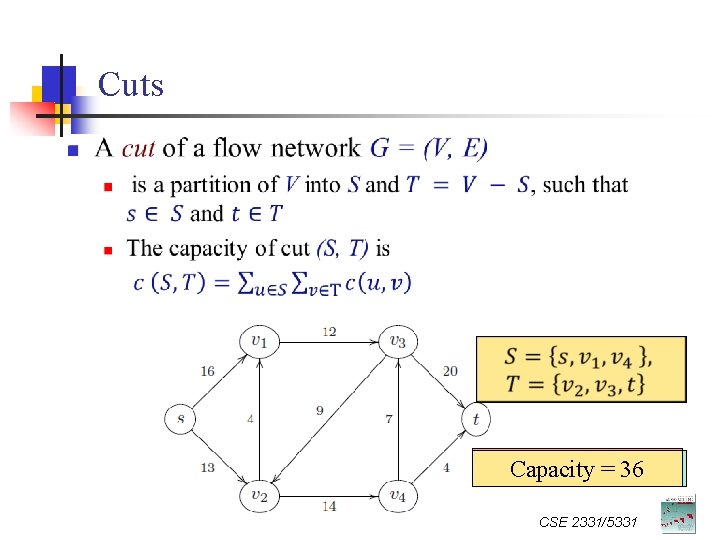
Max-Flow Min-Cut CSE 2331/5331

Cuts n Capacity 25 Capacity == 36 26 CSE 2331/5331

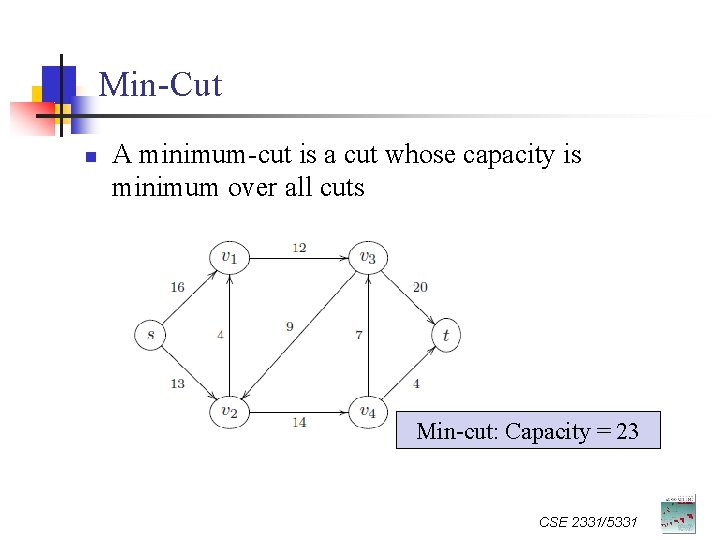
Min-Cut n A minimum-cut is a cut whose capacity is minimum over all cuts Min-cut: Capacity = 23 CSE 2331/5331

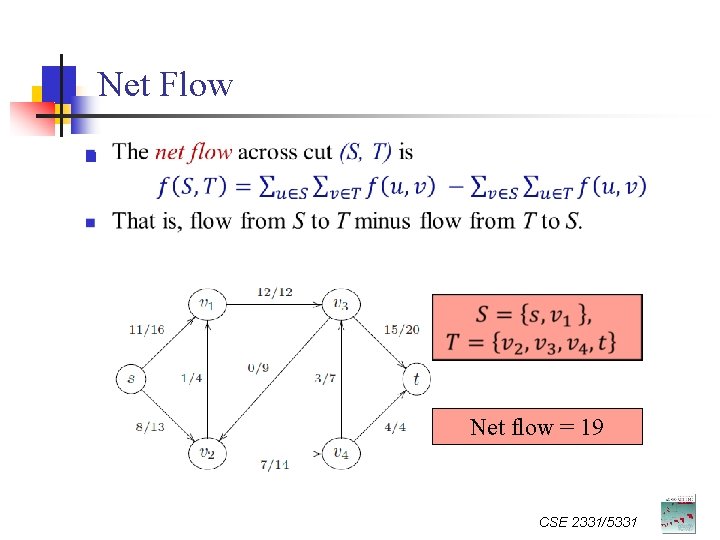
Net Flow n Net flow = 19 CSE 2331/5331

Net Flow Property I n CSE 2331/5331

Net Flow Property II n CSE 2331/5331

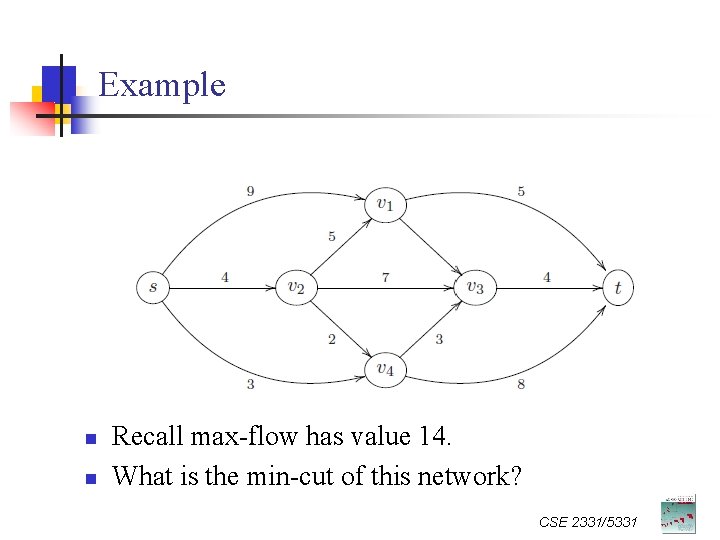
Example n n Recall max-flow has value 14. What is the min-cut of this network? CSE 2331/5331

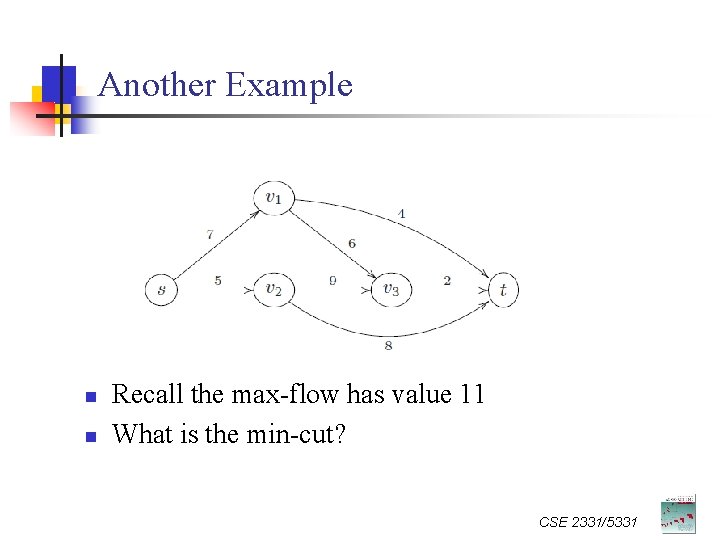
Another Example n n Recall the max-flow has value 11 What is the min-cut? CSE 2331/5331

n In general, how to compute Min-cut? CSE 2331/5331

Max-Flow Min-Cut Theorem n CSE 2331/5331

Proof Sketch n CSE 2331/5331

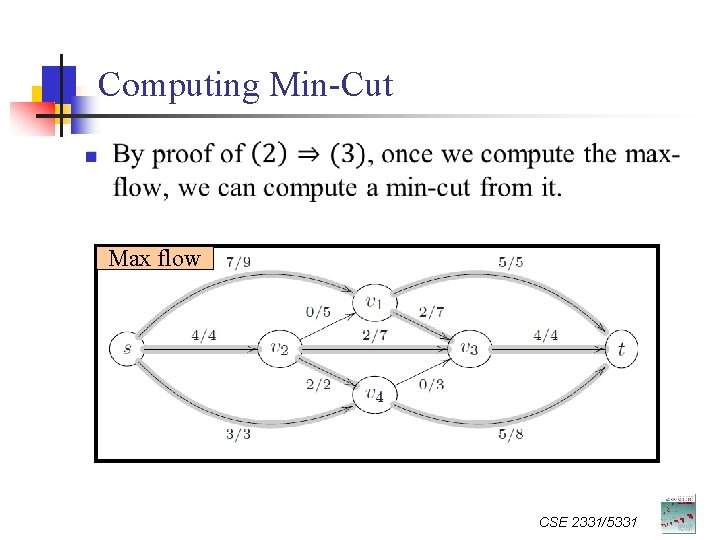
Computing Min-Cut n Max flow CSE 2331/5331

n Bipartite Matching CSE 2331/5331

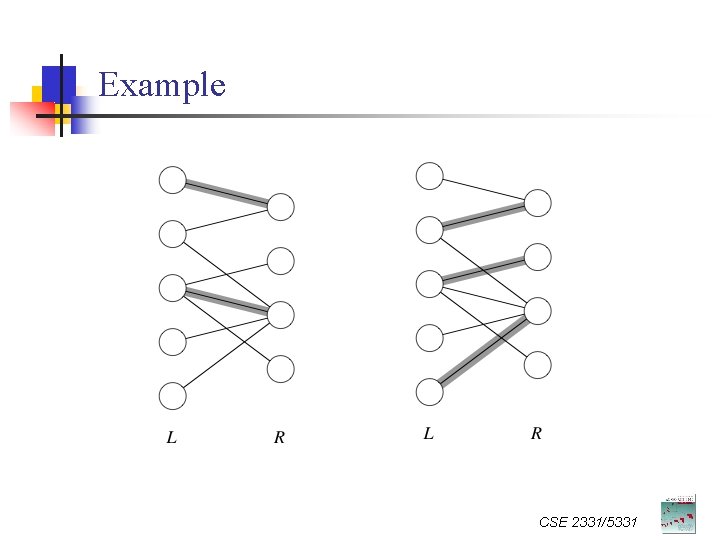
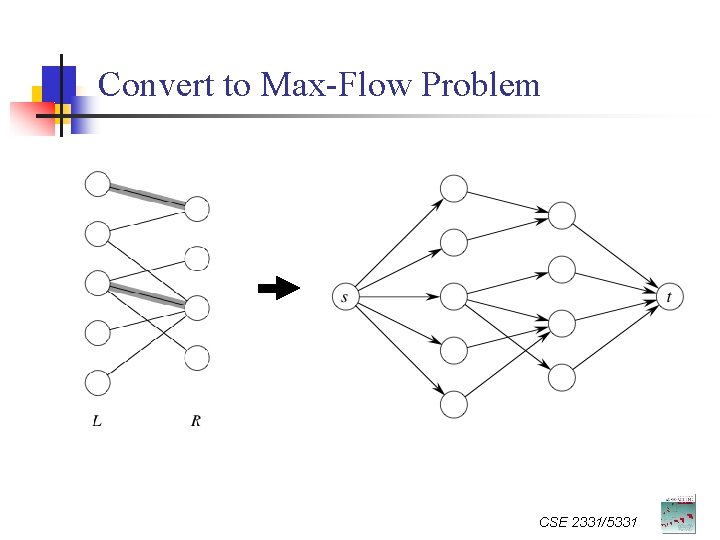
Matching in Bipartite Graph n Bipartite graph: n n A matching in bipartite graph is n n Graph G = (V, E) , where V = L R, and no edge in E crosses (L, R). A subset of edges M from E, where at most one edge from M is incident on any v V. Maximum matching in bipartite graph n A matching with largest cardinality CSE 2331/5331

Example CSE 2331/5331

Convert to Max-Flow Problem CSE 2331/5331

Main Observation n Lemma n n There is a one-to-one correspondence between a matching M and some integer-valued flow f. Furthermore, |M| = |f|. Proof. CSE 2331/5331

Integrality Theorem n n Ford-Fulkerson algorithm produces integer-valued flows if given integral capacities. Corollary: n The maximum matching for an unweighted bipartite graph can be computed in O(VE) time. CSE 2331/5331