CSE 20 DISCRETE MATH Clicker frequency CA Prof

CSE 20 DISCRETE MATH Clicker frequency: CA Prof. Shachar Lovett http: //cseweb. ucsd. edu/classes/wi 15/cse 20 -a/

Todays topics • Algorithms: what are they all about? • Sections 1. 1 -1. 2 in Jenkyns, Stephenson

What’s an algorithm? A. A step by step process B. Any way of solving complex problems C. Computer code D. I don’t know

An algorithm? • Definition: a step-by-step process • Each basic step is simple • Together they can compute very complicated things • What properties do we care about? A. It should have the correct format (“compile”) B. It should always terminate C. It should give the correct answer D. All of the above

Two algorithms Alg 1(real a, pos int n) Begin x 1. 0; i 1; Repeat x x * a; i i+1; Until i > n; Output x End. Alg 2(real a, pos int n) Begin x 1. 0; i n; While i>0 Do If (i is odd) Then x x * a; End; i i/2; If (i > 0) Then a a * a; End; Output x End What happens when we run Alg 1 with a = 4 and n = 5? What about Alg 2?

Two algorithms Alg 1(real a, pos int n) Begin x 1. 0; i 1; Repeat x x * a; i i+1; Until i > n; Output x End. A. Alg 1 doesn’t always work. B. Alg 2 doesn’t always work. C. Alg 1 is better than Alg 2 because it’s simpler. D. Alg 2 is better than Alg 1 because it’s faster. Alg 2(real a, pos int n) Begin x 1. 0; i n; While i>0 Do If (i is odd) Then x x * a; End; i i/2; If (i > 0) Then a a * a; End; Output x End.

Complexity of algorithms • Simplistic model: each basic operation (addition, multiplication, etc) takes unit time • Complexity of an algorithm = number of steps = running time • Depends on the input

Complexity of algorithms Alg 1(real a, pos int n) Begin x 1. 0; i 1; Repeat x x * a; i i+1; Until i > n; Output x End. • How many steps does this algorithm make? A. Constant number B. ~ n C. ~ log(n) D. ~ a*n E. Other

Complexity of algorithms Alg 1(real a, pos int n) Begin x 1. 0; i 1; Repeat x x * a; i i+1; Until i > n; Output x End. • How many steps does this algorithm make? A. Constant number B. ~ n C. ~ log(n) D. ~ a*n E. Other Running for n=1000000 takes ~3000000 steps

Complexity of algorithms • How many steps does this algorithm make? A. Constant number B. ~ n C. ~ log(n) D. ~ a*n E. Other Alg 2(real a, pos int n) Begin x 1. 0; i n; While i>0 Do If (i is odd) Then x x * a; End; i i/2; If (i > 0) Then a a * a; End; Output x End.

Complexity of algorithms • How many steps does this algorithm make? A. Constant number B. ~ n C. ~ log(n) D. ~ a*n E. Other Alg 2(real a, pos int n) Begin x 1. 0; i n; While i>0 Do If (i is odd) Then x x * a; End; i i/2; If (i > 0) Then a a * a; End; Output x End. Running for n=1000000 takes <= 120 steps

Pseudocode • Begin, End delimit list of steps. • Allowed types of steps • Assignment • Repeat-loop • If-Then-Else-End • While-loop • Walkthrough / Trace JS p. 10, 15

Casting out 9 s • Goal: check if a number n is divisible by 9 • Input: positive integer n • Algorithm: • While n >= 10: • Let b 1, …, bk be the digits of n in base 10 • n b 1+…+bk • Return TRUE if n=9, return FALSE otherwise Does it always terminate? Does it give the right answer? What is the complexity of this algorithm?

Notation and terms JS p. 9 • n DIV d • n MOD d • d divides evenly into n d is a factor (divisor) of n, n is a multiple of d d | n, n MOD d =0, If n is any integer and d is any positive integer, then there are (unique) integers q and r where n = d*q + r and 0 <= r < d

Solve the equation For what integer x do we have x DIV 5 = 14 and x MOD 5 = 2 ? A. No integers satisfy these equations at the same time. B. Any multiple of 5 works. C. Any non-multiple of 5 works. D. Only x = 72 works. E. None of the above / more than one of the above.

Solve the equation For what integer x do we have x MOD 5 = 2 ? A. -3 (and others) B. -2 (and others) C. All and only the multiples of 5 D. All and only the non-multiples of 5 E. None of the above / more than one of the above.

Why do we care? Round robin scheduling, secret sharing, parallel computation

Notation and terms JS p. 18 • Common divisor of two integers • GCD (x, y) Useful Facts • Lower bound • Upper bound • If y | x then … • Otherwise … GCD (x, y) >= 1 … even for negative x and y! GCD (x, y) <= MIN(|x|, |y|)

How can we compute GCD? • GCD(20, 30) = A. 20 B. 30 C. 5 D. 10 E. Other

How can we compute GCD? • One way: factoring to prime factors • Example: GCD(20, 30) • Factor 20 to prime factors: 20 = 2 * 5 • Factor 30 to prime factors: 30 = 2 * 3 * 5 • Common factor: 2 * 5 = 10

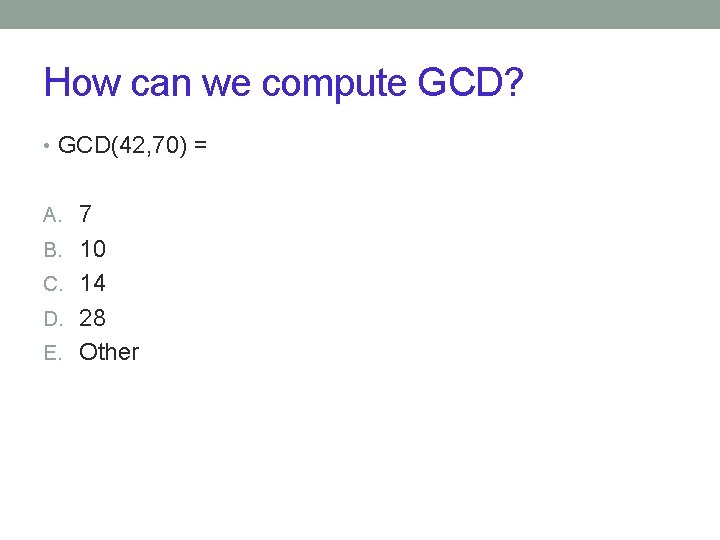
How can we compute GCD? • GCD(42, 70) = A. 7 B. 10 C. 14 D. 28 E. Other

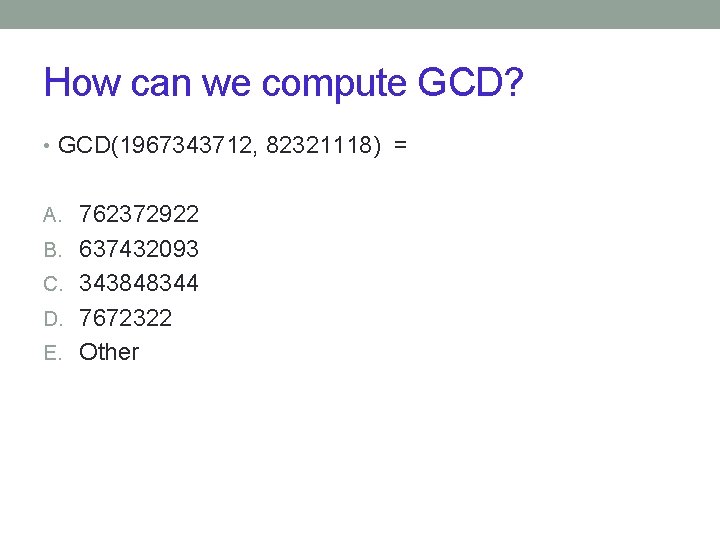
How can we compute GCD? • GCD(1967343712, 82321118) = A. 762372922 B. 637432093 C. 343848344 D. 7672322 E. Other

How can we compute GCD? • GCD(1967343712, 82321118) = … • Factoring numbers to prime factors is HARD • We don’t know any efficient way to factor large numbers • The security of e-commerce relies on this!!! (RSA encryption)

Euclid’s Algorithm JS p. 19 for computing GCD Euclid(int x, int y) Begin A x; B y; R A MOD B; While ( R>0 ) Do A B; B R; R A MOD B; End; Output B End. Why on Earth does this work? ? ?

Euclid’s Algorithm JS p. 19 for computing GCD Euclid(int x, int y) Begin A x; B y; R A MOD B; While ( R>0 ) Do A B; B R; R A MOD B; End; Output B End. Why on Earth does this work? ? ? Key fact: GCD(A, B) = GCD(B, A MOD B)

Euclid’s Algorithm JS p. 19 for computing GCD Euclid(int x, int y) Begin A x; B y; R A MOD B; While ( R>0 ) Do A B; B R; R A MOD B; End; Output B End. Why on Earth does this work? ? ? Key fact: GCD(A, B) = GCD(B, A MOD B) Correctness: GCD(A, B) start of loop = GCD(A, B) end of loop Termination: numbers get smaller

This week • Read sections 1. 1 -1. 3 in Jenkyns, Stephenson • Ask any questions you have about the course, expectations, requirements either in person or via TED • Next class … number representations (Section 1. 3)