CSE 185 Introduction to Computer Vision Image Filtering

CSE 185 Introduction to Computer Vision Image Filtering: Frequency Domain

Image filtering • Fourier transform and frequency domain – Frequency view of filtering – Hybrid images – Sampling • Reading: Chapters 3 • Some slides from James Hays, David Hoeim, Steve Seitz, …

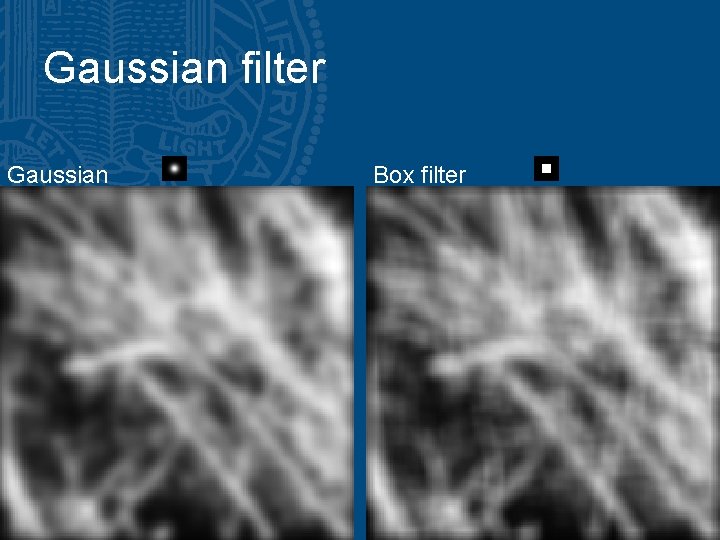
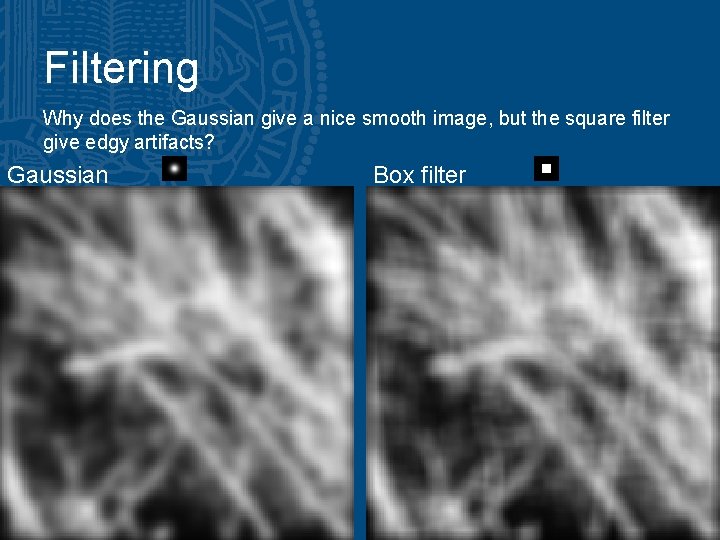
Gaussian filter Gaussian Box filter

Hybrid images • Filter one image with low-pass filter and the other with high-pass filter, and then superimpose them • A. Oliva, A. Torralba, P. G. Schyns, “Hybrid Images, ” SIGGRAPH 2006

Why do we get different, distance-dependent interpretations of hybrid images? ?

Why does a lower resolution image still make sense to us? What do we lose?

Compression How is it that a 4 MP image can be compressed to a few hundred KB without a noticeable change?

Thinking in terms of frequency • Convert an image into a frequency domain • Analyze the filter responses at different scale, orientation, and number of occurrence over time • Represent an image with basis filters

Jean Baptiste Joseph Fourier had crazy idea (1807): Any univariate function can be rewritten as a weighted sum of sines and cosines of different frequencies. . the manner in which the author arrives at these equations is not exempt of difficulties and. . . his analysis to integrate them still leaves something to be desired on the score of generality and even rigour. • Don’t believe it? – Neither did Lagrange, Laplace, Poisson and other big wigs – Not translated into English until 1878! • But it’s (mostly) true! – called Fourier Series – there are some subtle restrictions Legendre Laplace Lagrange

A sum of sines Our building block: Add enough of them to get any signal g(x) you want!

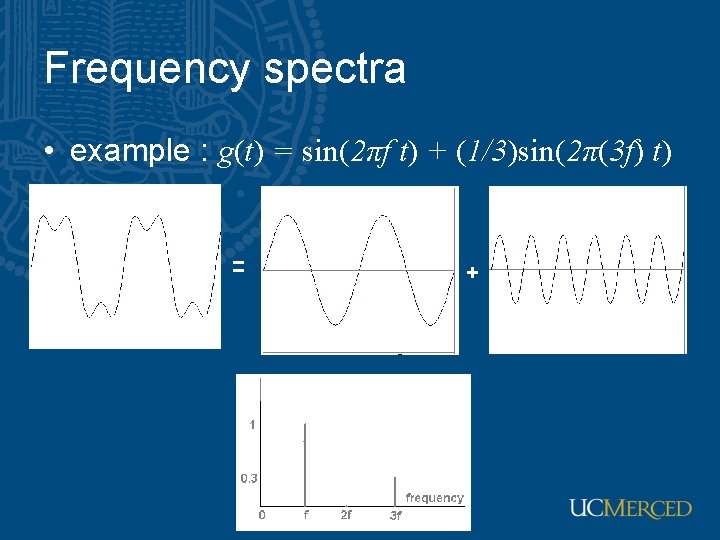
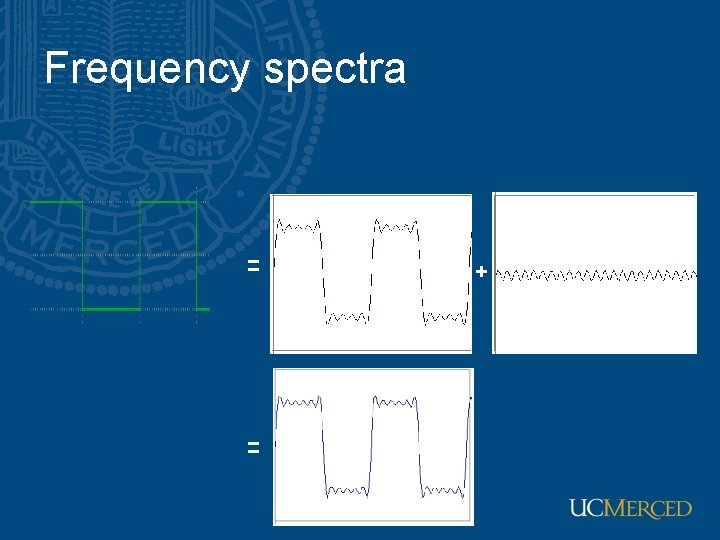
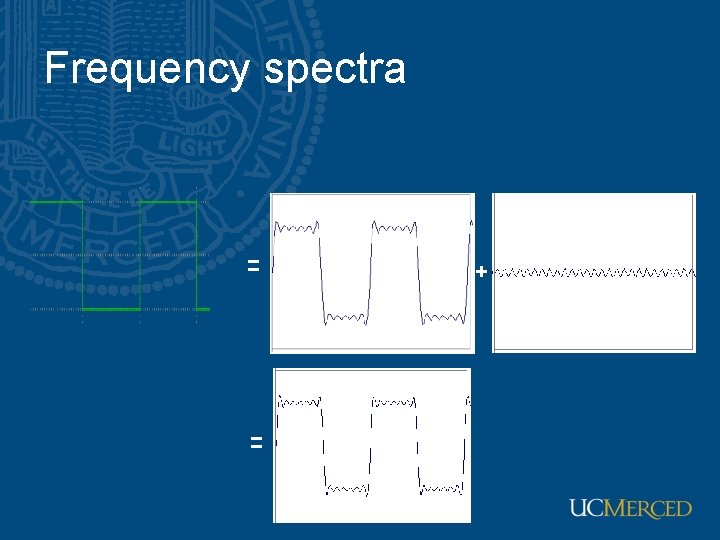
Frequency spectra • example : g(t) = sin(2πf t) + (1/3)sin(2π(3 f) t) = +

Frequency spectra

Frequency spectra = = +

Frequency spectra = = +

Frequency spectra = = +

Frequency spectra = = +

Frequency spectra = = +

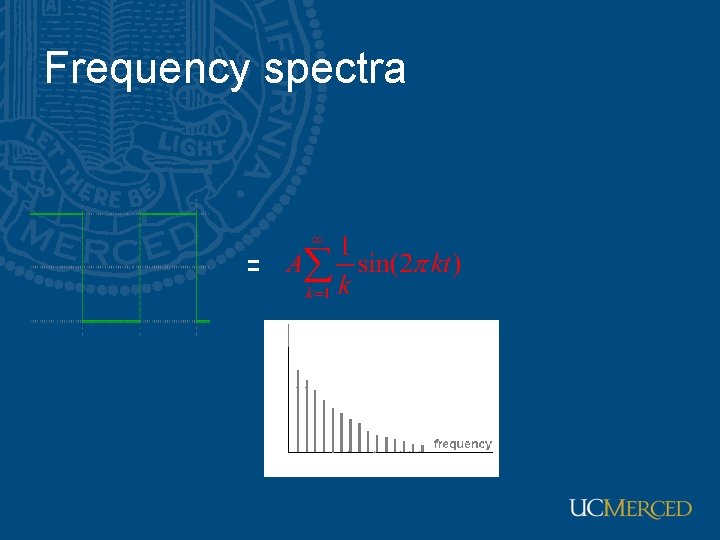
Frequency spectra =

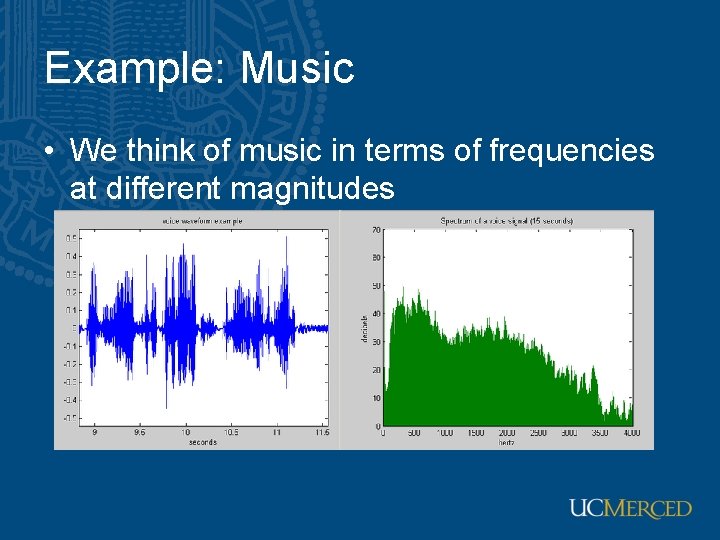
Example: Music • We think of music in terms of frequencies at different magnitudes

Fourier analysis in images Intensity Image Fourier Image

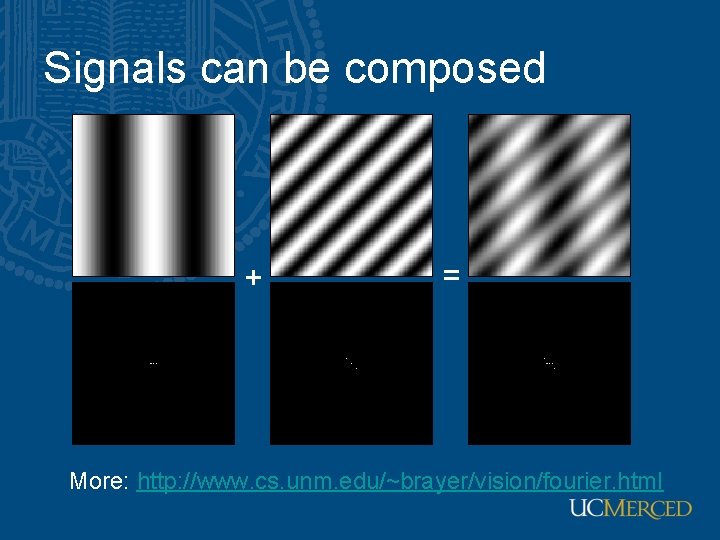
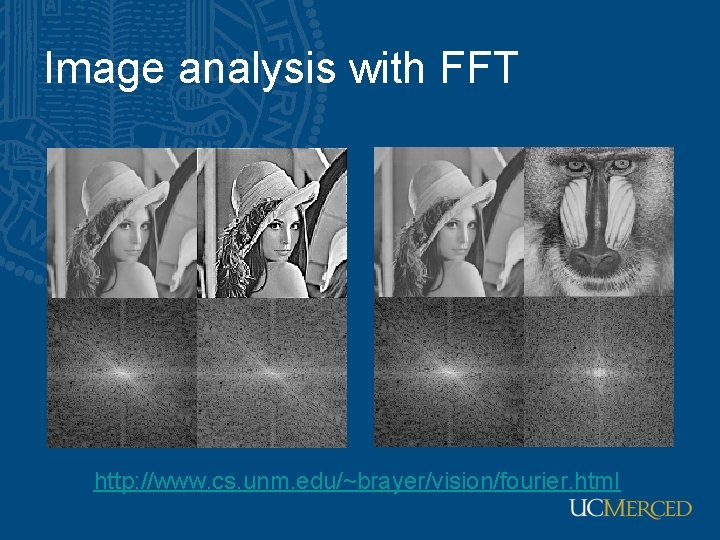
Signals can be composed + = More: http: //www. cs. unm. edu/~brayer/vision/fourier. html

Fourier transform • Fourier transform stores the magnitude and phase at each frequency – Magnitude encodes how much signal there is at a particular frequency – Phase encodes spatial information (indirectly) – For mathematical convenience, this is often notated in terms of real and complex numbers Amplitude: Phase:

Computing Fourier transform Continuous Discrete Fast Fourier Transform (FFT): Nlog. N k = -N/2. . N/2

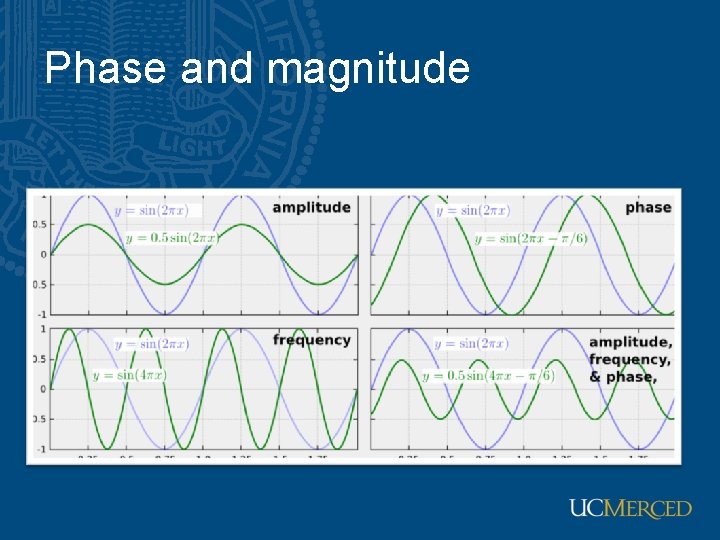
Phase and magnitude • Fourier transform of a real function is complex – difficult to plot – visualize instead, we can think of the phase and magnitude of the transform • Each frequency response is described by phase and magnitude • Phase: angle of complex transform • Magnitude: amplitude of complex transform • Curious fact – all natural images have about the same magnitude transform – hence, phase seems to matter, but magnitude largely doesn’t • Demonstration – take two pictures, swap the phase transforms, compute the inverse - what does the result look like?

Phase and magnitude

This is the magnitude transform of the cheetah pic

This is the phase transform of the cheetah pic

This is the magnitude transform of the zebra pic

This is the phase transform of the zebra pic

Reconstructio n with zebra phase, cheetah magnitude

Reconstruction with cheetah phase, zebra magnitude

The convolution theorem • The Fourier transform of the convolution of two functions is the product of their Fourier transforms • Convolution in the spatial domain is equivalent to multiplication in the frequency domain!

Properties of Fourier transform • Linearity • Fourier transform of a real signal is symmetric about the origin • The energy of the signal is the same as the energy of its Fourier transform See Szeliski Book (3. 4)

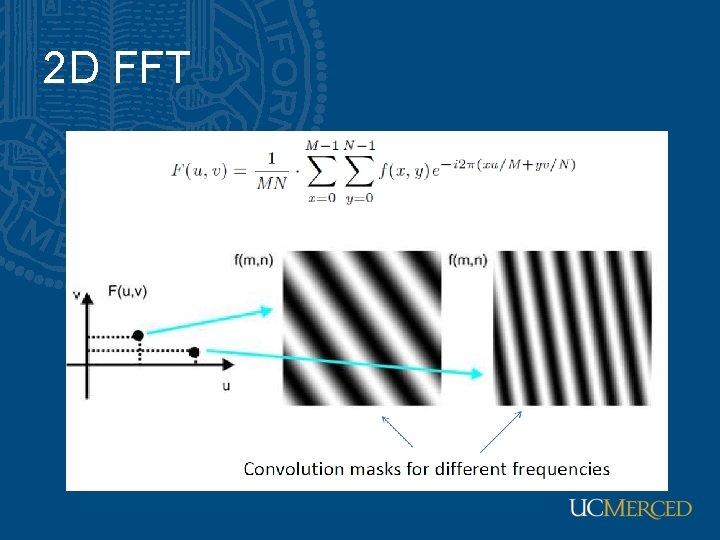
2 D FFT • Fourier transform (discrete case) Euler’s formula • Inverse Fourier transform: • u, v : the transform or frequency variables • x, y : the spatial or image variables

2 D FFT Sinusoid with frequency = 1 and its FFT

2 D FFT Sinusoid with frequency = 3 and its FFT

2 D FFT Sinusoid with frequency = 5 and its FFT

2 D FFT Sinusoid with frequency = 10 and its FFT

2 D FFT Sinusoid with frequency = 15 and its FFT

2 D FFT Sinusoid with varying frequency and their FFT

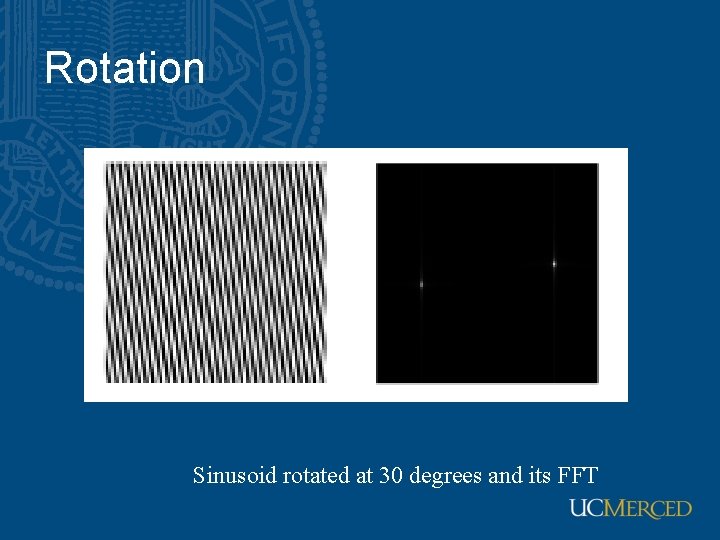
Rotation Sinusoid rotated at 30 degrees and its FFT

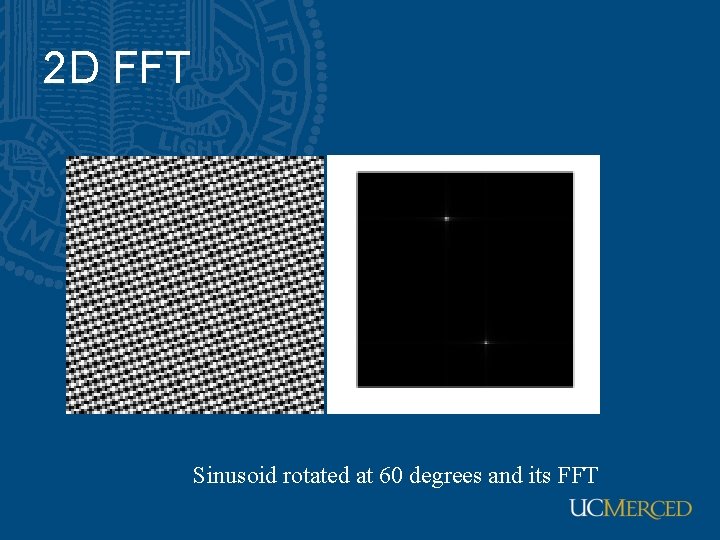
2 D FFT Sinusoid rotated at 60 degrees and its FFT

2 D FFT

Image analysis with FFT

Image analysis with FFT http: //www. cs. unm. edu/~brayer/vision/fourier. html

Filtering in spatial domain * = 1 0 -1 2 0 -2 1 0 -1

Filtering in frequency domain FFT = Inverse FFT

FFT in Matlab • Filtering with fft im = double(imread('cameraman. tif'))/255; [imh, imw] = size(im); hs = 50; % filter half-size fil = fspecial('gaussian', hs*2+1, 10); fftsize = 1024; % should be order of 2 (for speed) and include im_fft = fft 2(im, fftsize); % 1) fil_fft = fft 2(fil, fftsize); % 2) image im_fil_fft = im_fft. * fil_fft; % 3) im_fil = ifft 2(im_fil_fft); % 4) im_fil = im_fil(1+hs: size(im, 1)+hs, 1+hs: size(im, 2)+hs); % 5) figure, imshow(im); figure, imshow(im_fil); padding fft im with padding fft fil, pad to same size as multiply fft images inverse fft 2 remove padding • Displaying with fft figure(1), imagesc(log(abs(fftshift(im_fft)))), axis image, colormap jet

Questions Which has more information, the phase or the magnitude? What happens if you take the phase from one image and combine it with the magnitude from another image?

Filtering Why does the Gaussian give a nice smooth image, but the square filter give edgy artifacts? Gaussian Box filter

Gaussian filter Gaussian

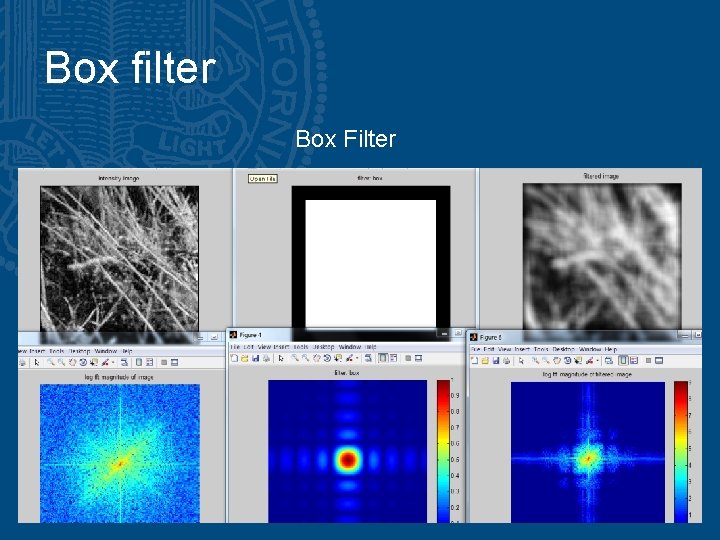
Box filter Box Filter

Why do we get different, distance-dependent interpretations of hybrid images? ?

Salvador Dali invented Hybrid Images? Salvador Dali “Gala Contemplating the Mediterranean Sea, which at 30 meters becomes the portrait of Abraham Lincoln”, 1976

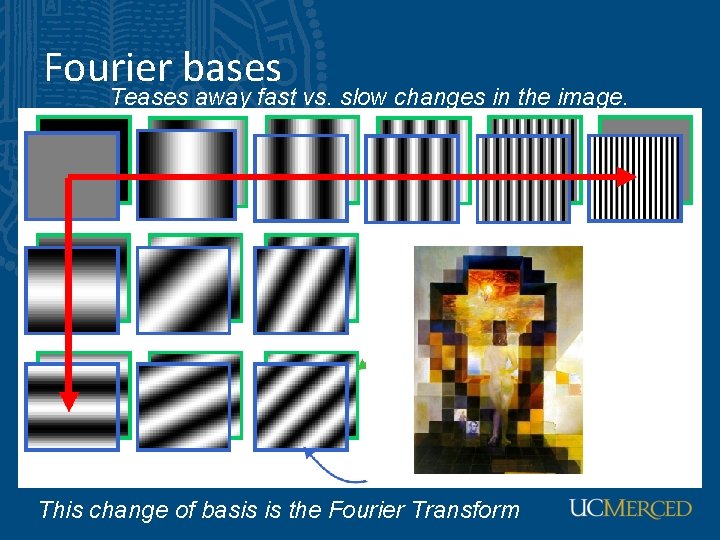
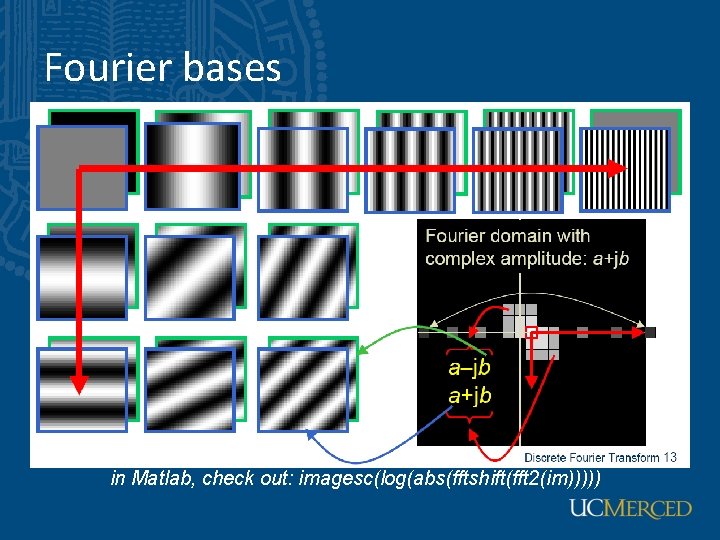
Fourier bases Teases away fast vs. slow changes in the image. This change of basis is the Fourier Transform

Fourier bases in Matlab, check out: imagesc(log(abs(fftshift(fft 2(im)))))

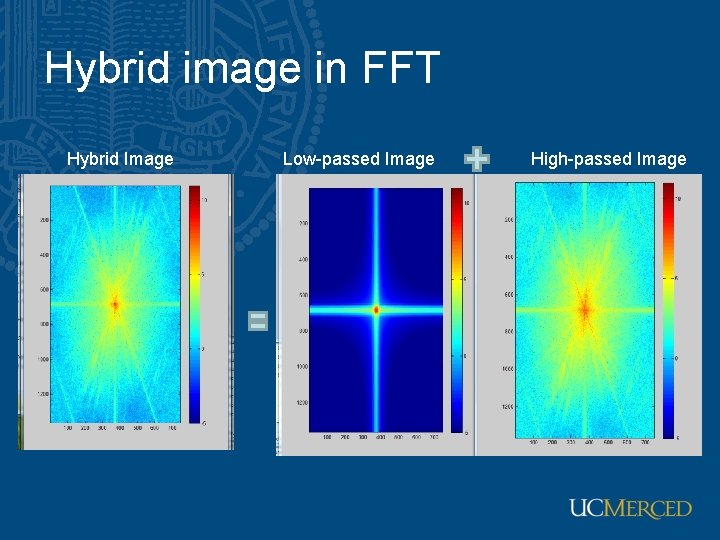
Hybrid image in FFT Hybrid Image Low-passed Image High-passed Image

Application: Hybrid images • Combine low-frequency of one image with high-frequency of another one • Sad faces when looked closely • Happy faces when looked a few meters away • A. Oliva, A. Torralba, P. G. Schyns, “Hybrid Images, ” SIGGRAPH 2006

Sampling Why does a lower resolution image still make sense to us? What do we lose?

Why does a lower resolution image still make sense to us? What do we lose?

Subsampling by a factor of 2 Throw away every other row and column to create a 1/2 size image

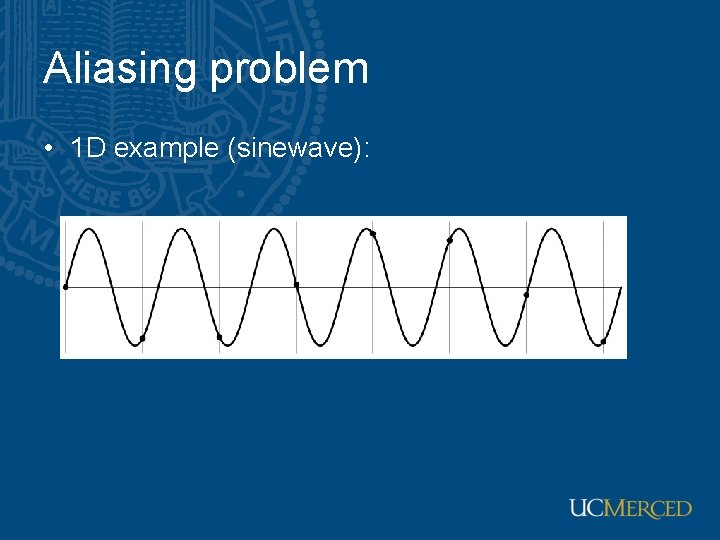
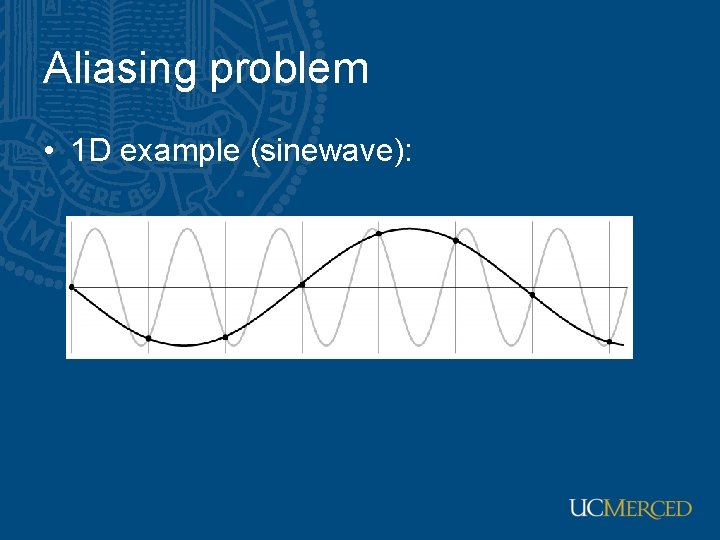
Aliasing problem • 1 D example (sinewave):

Aliasing problem • 1 D example (sinewave):

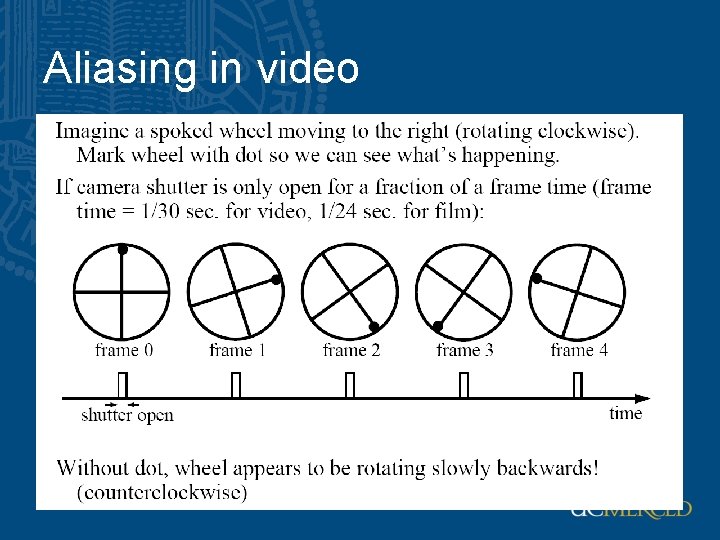
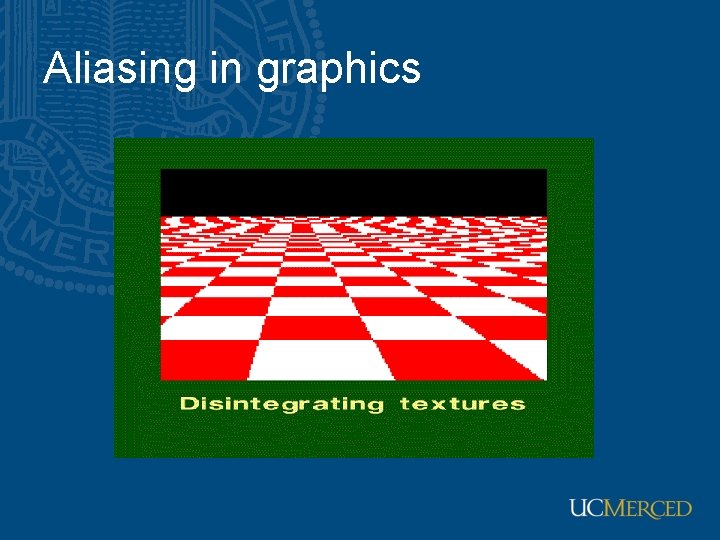
Aliasing problem • Sub-sampling may be dangerous…. • Characteristic errors may appear: – “Wagon wheels rolling the wrong way in movies” – “Checkerboards disintegrate in ray tracing” – “Striped shirts look funny on color television”

Aliasing in video

Aliasing in graphics

Resample the checkerboard by taking one sample at each circle. In the case of the top left board, new representation is reasonable. Top right also yields a reasonable representation. Bottom left is all black (dubious) and bottom right has checks that are too big. Sampling scheme is crucially related to frequency

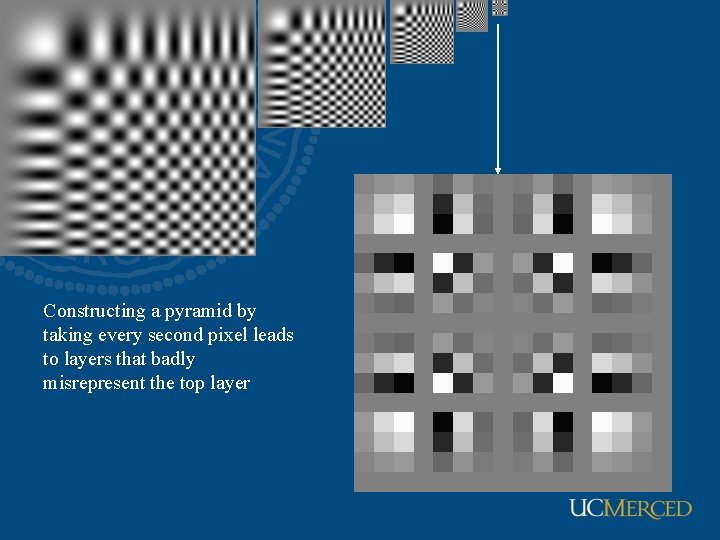
Constructing a pyramid by taking every second pixel leads to layers that badly misrepresent the top layer

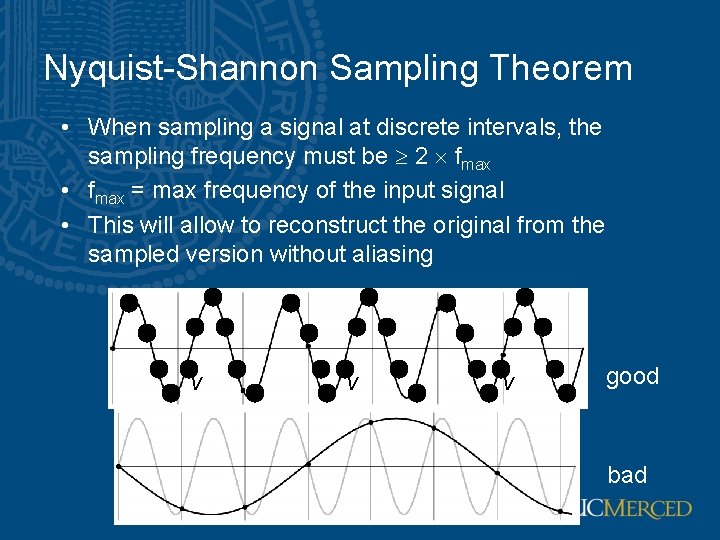
Nyquist-Shannon Sampling Theorem • When sampling a signal at discrete intervals, the sampling frequency must be 2 fmax • fmax = max frequency of the input signal • This will allow to reconstruct the original from the sampled version without aliasing v v v good bad

Anti-aliasing Solutions: • Sample more often • Get rid of all frequencies that are greater than half the new sampling frequency – Will lose information – But it’s better than aliasing – Apply a smoothing filter

Algorithm for downsampling by factor of 2 1. Start with image(h, w) 2. Apply low-pass filter im_blur = imfilter(image, fspecial(‘gaussian’, 7, 1)) 3. Sample every other pixel im_small = im_blur(1: 2: end, 1: 2: end);

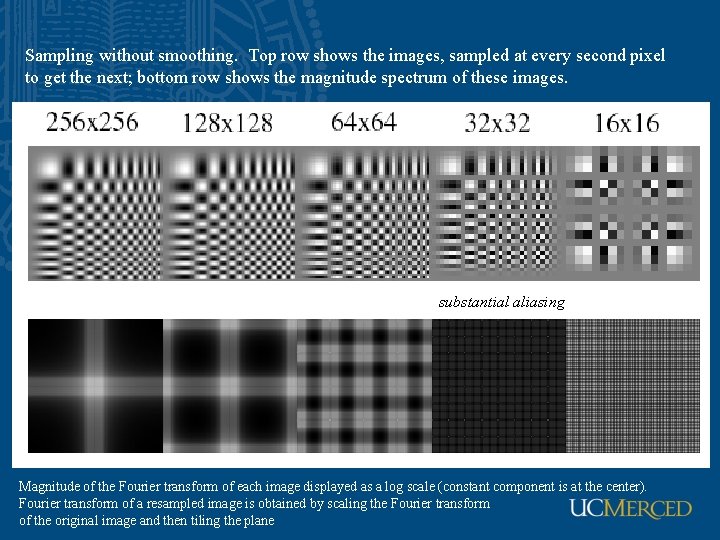
Sampling without smoothing. Top row shows the images, sampled at every second pixel to get the next; bottom row shows the magnitude spectrum of these images. substantial aliasing Magnitude of the Fourier transform of each image displayed as a log scale (constant component is at the center). Fourier transform of a resampled image is obtained by scaling the Fourier transform of the original image and then tiling the plane

Sampling with smoothing (small σ). Top row shows the images. We get the next image by smoothing the image with a Gaussian with σ=1 pixel, then sampling at every second pixel to get the next; bottom row shows the magnitude spectrum of these images. reducing aliasing Low pass filter suppresses high frequency components with less aliasing

Sampling with smoothing (large σ). Top row shows the images. We get the next image by smoothing the image with a Gaussian with σ=2 pixels, then sampling at every second pixel to get the next; bottom row shows the magnitude spectrum of these images. lose details Large σ less aliasing, but with little detail Gaussian is not an ideal low-pass filter

Subsampling without prefiltering 1/2 1/4 (2 x zoom) 1/8 (4 x zoom)

Subsampling with Gaussian prefiltering Gaussian 1/2 G 1/4 G 1/8

Clues from human perception • Early processing in humans filters for various orientations and scales of frequency • Perceptual cues in the mid-high frequencies dominate perception • When we see an image from far away, we are effectively subsampling it Early Visual Processing: Multi-scale edge and blob filters

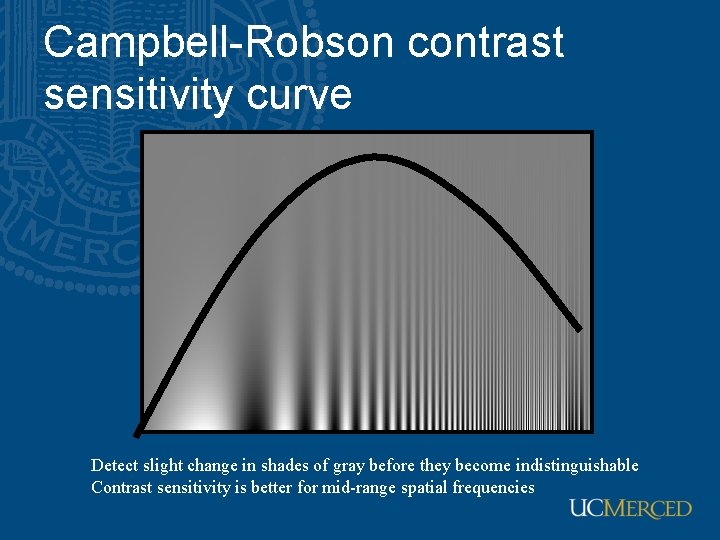
Campbell-Robson contrast sensitivity curve Detect slight change in shades of gray before they become indistinguishable Contrast sensitivity is better for mid-range spatial frequencies

Things to remember • Sometimes it makes sense to think of images and filtering in the frequency domain – Fourier analysis • Can be faster to filter using FFT for large images (N log. N vs. N 2 for autocorrelation) • Images are mostly smooth – Basis for compression • Remember to low-pass before sampling

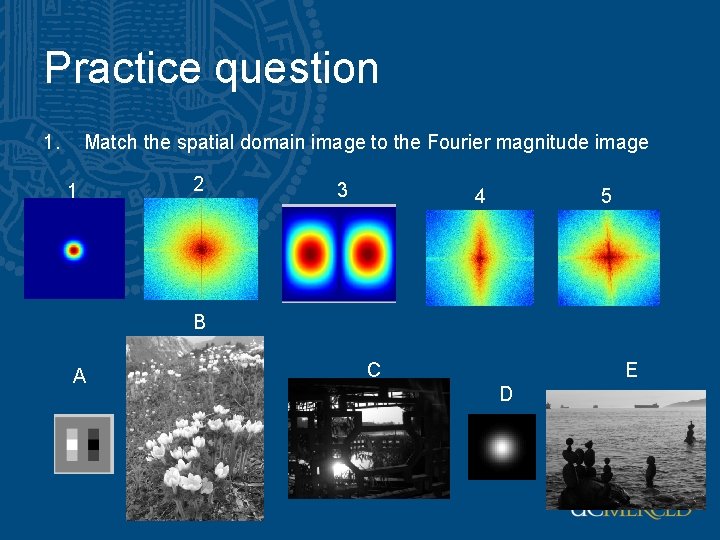
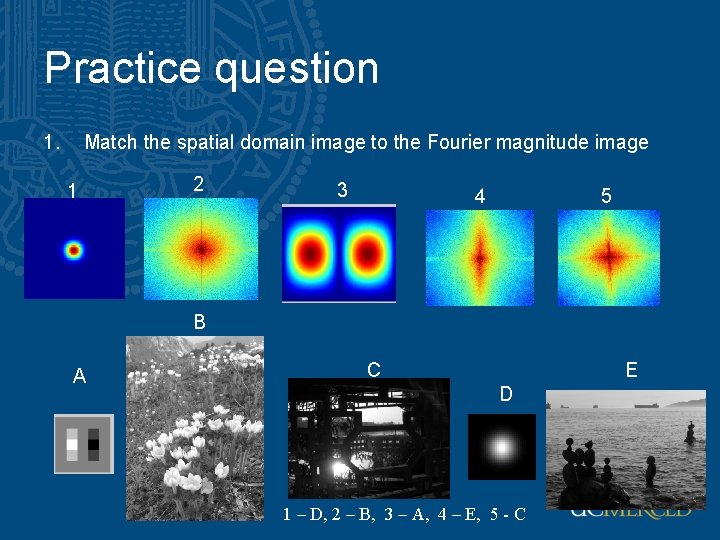
Practice question 1. Match the spatial domain image to the Fourier magnitude image 1 2 3 4 5 B A C E D

Practice question 1. Match the spatial domain image to the Fourier magnitude image 1 2 3 4 5 B A C E D 1 – D, 2 – B, 3 – A, 4 – E, 5 - C