CSE 143 Lecture 16 Sorting Merge Sort Based

CSE 143 Lecture 16 Sorting & Merge Sort Based on slides created by Ethan Apter & Marty Stepp 1

Sorting • sorting: Rearranging the values in an array or collection into a specific order (usually into their "natural ordering"). – one of the fundamental problems in computer science – can be solved in many ways: • there are many sorting algorithms • some are faster/slower than others • some use more/less memory than others • some work better with specific kinds of data • some can utilize multiple computers / processors, . . . – comparison-based sorting : determining order by comparing pairs of elements: • <, >, compare. To, … 2

Sorting algorithms • • • bubble sort: swap adjacent pairs that are out of order selection sort: look for the smallest element, move to front insertion sort: build an increasingly large sorted front portion merge sort: recursively divide the array in half and sort it heap sort: place the values into a sorted tree structure quick sort: recursively partition array based on a middle value other specialized sorting algorithms: • bucket sort: cluster elements into smaller groups, sort them • radix sort: sort integers by last digit, then 2 nd to last, then. . . • . . . 3

Selection sort • selection sort: Orders a list of values by repeatedly putting the smallest or largest unplaced value into its final position. The algorithm: – Look through the list to find the smallest value. – Swap it so that it is at index 0. – Look through the list to find the second-smallest value. – Swap it so that it is at index 1. . – Repeat until all values are in their proper places. 4

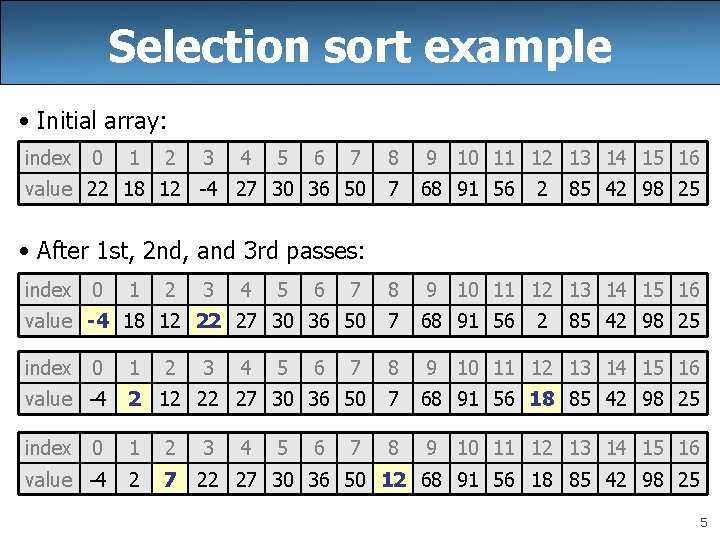
Selection sort example • Initial array: index 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 value 22 18 12 -4 27 30 36 50 7 68 91 56 7 8 9 10 11 12 13 14 15 16 value -4 18 12 22 27 30 36 50 7 68 91 56 index 0 1 7 8 9 10 11 12 13 14 15 16 value -4 2 12 22 27 30 36 50 7 68 91 56 18 85 42 98 25 index 0 1 2 3 8 9 10 11 12 13 14 15 16 value -4 2 7 22 27 30 36 50 12 68 91 56 18 85 42 98 25 2 85 42 98 25 • After 1 st, 2 nd, and 3 rd passes: index 0 1 2 2 3 3 4 4 4 5 5 5 6 6 6 7 2 85 42 98 25 5

Selection sort code // Rearranges the elements of a into sorted order using // the selection sort algorithm. public static void selection. Sort(int[] a) { for (int i = 0; i < a. length - 1; i++) { // find index of smallest remaining value int min = i; for (int j = i + 1; j < a. length; j++) { if (a[j] < a[min]) { min = j; } } // swap smallest value its proper place, a[i] swap(a, i, min); 6

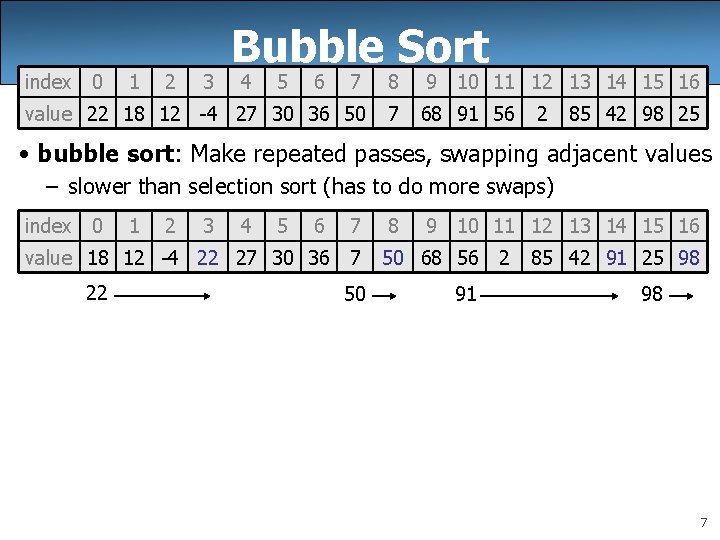
index 0 1 2 3 Bubble Sort 4 5 6 7 8 9 10 11 12 13 14 15 16 value 22 18 12 -4 27 30 36 50 7 68 91 56 2 85 42 98 25 • bubble sort: Make repeated passes, swapping adjacent values – slower than selection sort (has to do more swaps) index 0 1 2 3 4 5 6 7 value 18 12 -4 22 27 30 36 7 22 50 8 9 10 11 12 13 14 15 16 50 68 56 2 91 85 42 91 25 98 98 7

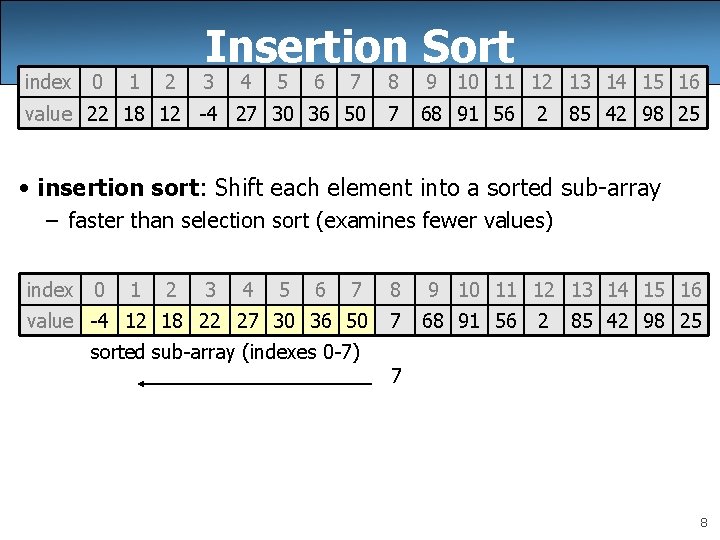
index 0 1 2 Insertion Sort 3 4 5 6 7 8 9 10 11 12 13 14 15 16 value 22 18 12 -4 27 30 36 50 7 68 91 56 2 85 42 98 25 • insertion sort: Shift each element into a sorted sub-array – faster than selection sort (examines fewer values) index 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 value -4 12 18 22 27 30 36 50 7 68 91 56 sorted sub-array (indexes 0 -7) 2 85 42 98 25 7 8

O(n 2) Algorithms • Insertion sort: add values to a sorted list so as to maintain sorted order – the “sorted list” can originally be empty so that you can sort many values – similar to what we did in Sorted. Int. List (HW#1) • Selection sort: scan an unsorted list for the smallest value, and move the smallest value to the front. Repeat this process for the remaining values until the whole list is sorted • Both insertion sort and selection sort are O(n 2) algorithms 9

Merge Sort • Merge sort: – divide a list into two halves – sort the halves – recombine the sorted halves into a sorted whole • Merge sort is an example of a “divide and conquer” algorithm • divide and conquer algorithm: an algorithm that repeatedly divides the given problem into smaller pieces that can be solved more easily – it’s easier to sort the two small lists than the one big list 10

Merge Sort Picture 22 22 22 0 1 2 3 4 5 6 7 22 18 12 -4 58 7 31 42 18 18 12 18 18 -4 12 -4 -4 12 22 -4 12 18 58 58 -4 58 12 7 22 7 7 31 58 31 31 42 0 1 2 3 4 5 6 7 -4 7 12 18 22 31 42 58 42 42 s p l i t 42 42 58 m e r g e 11

merge. Into • Merge sort: We’re going to write this part first – divide a list into two halves – sort the halves – recombine the sorted halves into a sorted whole • We’re going to write the following method: // post: copies the values from list 1 and list 2 // into result so that the values in result // are in sorted order private static void merge. Into(int[] result, int[] list 1, int[] list 2) {. . . } 12

merge. Into // post: copies the values from list 1 and list 2 // into result so that the values in result // are in sorted order private static void merge. Into(int[] result, int[] list 1, int[] list 2) { 13

merge. Into • So how do we actually merge the two sorted lists into one sorted result list? • One (wrong) way would just be to blindly copy the values from the two sorted lists into the result list and then sort the result list – this doesn’t take advantage of the fact that the two lists are already sorted • Instead, we’ll repeatedly select the smallest value from both sorted lists and put this value into the result list – because the two sorted lists are sorted, we know that their smallest values are found at the front 14

merge. Into • So to compare the smallest values, we’ll do something like this if (list 1[0] <= list 2[0]) result[0] = list 1[0]; else result[0] = list 2[0]; • Obviously, this only handles the very first value • We need to use a loop and update our indexes in order to get this working correctly • But how many indexes do we need? 15

merge. Into Indexes • We have three arrays, so we need three indexes – we need an index for list 1, which tells us how many values from list 1 we’ve copied so far – we need an index for list 2, which tells us how many values from list 2 we’ve copied so far – we need an index for result, which tells us how many values total we’ve copied from list 1 and list 2 • we could just use the sum of the first two indexes for this index • So we have the following indexes: int i 1 = 0; // index for list 1 int i 2 = 0; // index for list 2 int i = 0; // index for result (equals i 1 + i 2) 16

merge. Into • So now we’ll update our previous code to use a loop and our indexes int i 1 = 0; int i 2 = 0; for (int i = 0; i if (list 1[i 1] result[i] i 1++; } else { result[i] i 2++; } } < result. length; i++) { <= list 2[i 2]) { = list 1[i 1]; = list 2[i 2]; 17

merge. Into • So now we’ll update our previous code to use a loop and our indexes int i 1 = 0; int i 2 = 0; for (int i = 0; i if (list 1[i 1] result[i] i 1++; } else { result[i] i 2++; } } < result. length; i++) { <= list 2[i 2]) { = list 1[i 1]; But this doesn’t quite work! = list 2[i 2]; 18

merge. Into • Right now, our code always compares a value from list 1 with a value from list 2 • But, because we’re coping a single value into result per loop iteration, we’ll finish copying all the values from one of the sorted lists before the other • So we also need to check if we’ve copied all the values from a list – if we’ve already copied all the values from list 1, copy the value from list 2 – if we’ve already copied all the values from list 2, copy the value from list 1 19

merge. Into • Updated merge. Into code: int i 1 = 0; int i 2 = 0; for (int i = 0; i < result. length; i++) { if (i 2 >= list 2. length || (i 1 < list 1. length && list 1[i 1] <= list 2[i 2])) { result[i] = list 1[i 1]; i 1++; This code is a little } else { subtle. It relies on the result[i] = list 2[i 2]; short-circuiting property i 2++; of && and || } } • This code is finished (it just needs to be put inside the method header) 20

merge. Into Final Code private static void merge. Into(int[] result, int[] list 1, int[] list 2) { int i 1 = 0; int i 2 = 0; for (int i = 0; i < result. length; i++) { if (i 2 >= list 2. length || (i 1 < list 1. length && list 1[i 1] <= list 2[i 2])) { result[i] = list 1[i 1]; i 1++; } else { result[i] = list 2[i 2]; i 2++; } } } 21

merge. Into’s Preconditions • But notice our merge. Into method has some preconditions: – both list 1 and list 2 must already be sorted – result’s length must equal list 1’s length plus list 2’s length • Updated comment: // pre: // // post: // // list 1 and list 2 are sorted result. length == list 1. length + list 2. length copies the values from list 1 and list 2 into result so that the values in result are in sorted order 22

Merge Sort • Recall that merge sort consists of the following steps: – divide a list into two halves – sort the halves – recombine the sorted halves into a sorted whole • We’ve written the “recombine” step (merge. Into) – But now we have to write the first two steps • Let’s define our public sort method: // post: sorts the given array into non-decreasing order public static void sort(int[] list) {. . . } 23

Merge Sort // post: sorts the given array into non-decreasing order public static void sort(int[] list) { // Divide the list into two halves // Sort the halves // Recombine the sorted halves into a sorted whole 24

Dividing the List in Half • First we have to divide our list into two lists that are half the size of the original list • To do this, we need to create a place to store these two lists – we’ll create two new integer arrays • A first attempt at creating the two new integer arrays: int[] list 1 = new int[list. length / 2]; int[] list 2 = new int[list. length / 2]; • But what if the length of our array is odd? – e. g. if list. length == 1001, then list. length / 2 == 500 • and we’ll miss an element! – we need to handle the odd case 25

Dividing the List in Half • Here’s some better code: int[] list 1 = new int[list. length / 2]; int[] list 2 = new int[list. length - list. length / 2]; • And now we can also copy the first half of the list into list 1 and the second half of the list into list 2 • Here’s the code for copying the values for (int i = list 1[i] for (int i = list 2[i] 0; i < list 1. length; i++) = list[i]; 0; i < list 2. length; i++) = list[i + list 1. length]; 26

Merge Sort • So here’s our code for sort so far: public static void sort(int[] list) { // Divide the list into two halves int[] list 1 = new int[list. length / 2]; int[] list 2 = new int[list. length - list. length / 2]; for (int i = 0; i < list 1. length; i++) list 1[i] = list[i]; for (int i = 0; i < list 2. length; i++) list 2[i] = list[i + list 1. length]; // Sort the halves // Recombine the sorted halves into a sorted whole } 27

Sorting the Halves • But how will we sort the two halves? – if only we had a method that could sort a list. . . – oh wait! That’s what we’re writing! • If we’re going to make our sort method recursive, we need to modify it to have a base case – what’s an easy list to sort? • the empty list (sorted by definition) • the list with one element (sorted by definition) • So if our sort is called on lists with size <= 1, we don’t have to do anything 28

Base Case • Modified sort to have a base case: public static void sort(int[] list) { if (list. length > 1) { int[] list 1 = new int[list. length / 2]; int[] list 2 = new int[list. length - list. length / 2]; for (int i = 0; i < list 1. length; i++) list 1[i] = list[i]; for (int i = 0; i < list 2. length; i++) list 2[i] = list[i + list 1. length]; . . . } } • Now we can just call sort on the two halves (list 1 and list 2), and we’ll eventually reach our base case 29

Sorting the Halves • Modified sort that calls itself to sort the two halves: public static void sort(int[] list) { if (list. length > 1) { int[] list 1 = new int[list. length / 2]; int[] list 2 = new int[list. length - list. length / 2]; for (int i = 0; i < list 1. length; i++) list 1[i] = list[i]; for (int i = 0; i < list 2. length; i++) list 2[i] = list[i + list 1. length]; sort(list 1); sort(list 2); . . . } } • Finally, we just merge the two halves into the original list 30

sort Final Code • Final version of sort: public static void sort(int[] list) { if (list. length > 1) { int[] list 1 = new int[list. length / 2]; int[] list 2 = new int[list. length - list. length / 2]; for (int i = 0; i < list 1. length; i++) list 1[i] = list[i]; for (int i = 0; i < list 2. length; i++) list 2[i] = list[i + list 1. length]; sort(list 1); sort(list 2); merge. Into(list, list 1, list 2); } } 31

Merge Sort is Stable • Merge sort can be written so that it is a stable sort • stable sort: a sorting algorithm that maintains the relative positions of equal elements – So, if there are multiple 3 s in a list, a stable sort will put • put the 3 that occurred first before the others • put the 3 that occurred second after the first and before the others • . . . • the 3 that occurred last after the others • And the way we’ve written merge sort makes it stable – because of how we divided our list into halves in sort – and because of how we break ties during the comparison of values in merge. Into 32

Analyzing Our Performance • Let’s compare the performance of our merge sort to Sun’s Arrays. sort • Here’s a sample run from Int. Array. Sorter. java (on the website) run on a 2. 53 GHz Intel Core 2 Duo Macbook This program compares the performance of the merge sort written in CSE 143 against the performance of Sun's Arrays. sort method by timing both methods on random, identical int arrays of length 2500000 Sun's time: 0. 507 seconds Our time: 1. 135 seconds Ratio (Sun's/our): 2. 24 33

Analyzing Our Performance • Sun’s sort is faster than ours – but only by a factor of about 2. 5 • That’s really good! It didn’t take us long to write this, and Sun’s Arrays. sort is a professional sorting method • Sun has had years to fine-tune the performance of Arrays. sort, and yet we wrote a reasonably competitive merge sort in less than an hour! • So what’s the complexity of merge sort? 34

sort Final Code • Final version of sort: public static void sort(int[] list) { if (list. length > 1) { int[] list 1 = new int[list. length / 2]; int[] list 2 = new int[list. length - list. length / 2]; for (int i = 0; i < list 1. length; i++) list 1[i] = list[i]; for (int i = 0; i < list 2. length; i++) list 2[i] = list[i + list 1. length]; sort(list 1); sort(list 2); merge. Into(list, list 1, list 2); } } 35

merge. Into Final Code private static void merge. Into(int[] result, int[] list 1, int[] list 2) { int i 1 = 0; int i 2 = 0; for (int i = 0; i < result. length; i++) { if (i 2 >= list 2. length || (i 1 < list 1. length && list 1[i 1] <= list 2[i 2])) { result[i] = list 1[i 1]; i 1++; } else { result[i] = list 2[i 2]; i 2++; } } } 36

Complexity of Merge Sort • To determine the time complexity, let’s break our merge sort into pieces and analyze the pieces • Remember, merge sort consists of: – divide a list into two halves – sort the halves – recombine the sorted halves into a sorted whole • Dividing the list in half and recombining the lists are pretty easy to analyze: – both have O(n) time complexity • But what about sorting the halves? 37

Complexity of Merge Sort • We can think of merge sort as occurring in levels – – at the first level, we want to sort the whole list at the second level, we want to sort the two half lists at the third level, we want to sort the four quarter lists. . . • We know there’s O(n) work at each level from dividing/recombining the lists • But how many levels are there? – if we can figure this out, our time complexity is just O(n * num_levels) 38

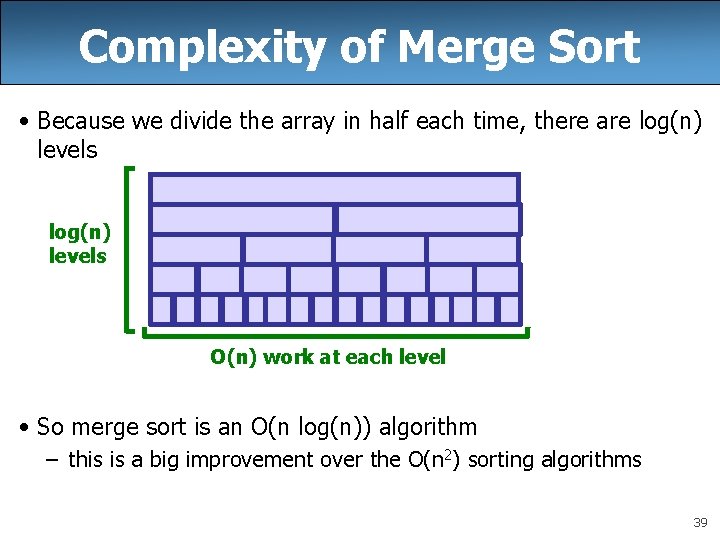
Complexity of Merge Sort • Because we divide the array in half each time, there are log(n) levels O(n) work at each level • So merge sort is an O(n log(n)) algorithm – this is a big improvement over the O(n 2) sorting algorithms 39

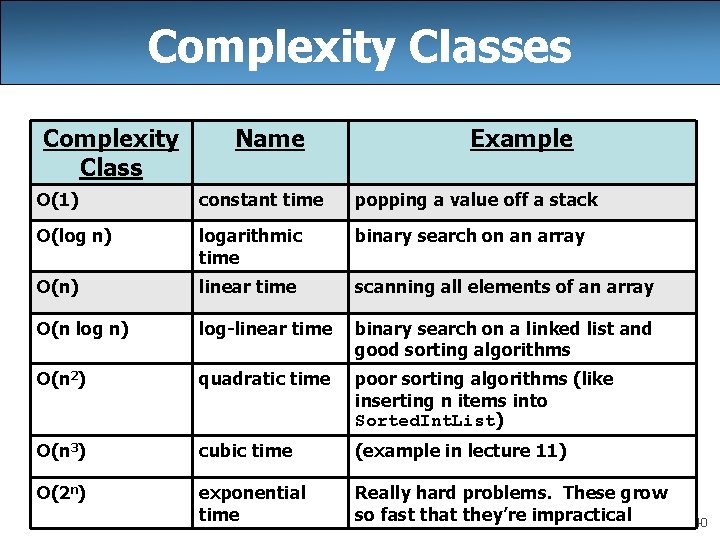
Complexity Classes Complexity Class Name Example O(1) constant time popping a value off a stack O(log n) logarithmic time binary search on an array O(n) linear time scanning all elements of an array O(n log n) log-linear time binary search on a linked list and good sorting algorithms O(n 2) quadratic time poor sorting algorithms (like inserting n items into Sorted. Int. List) O(n 3) cubic time (example in lecture 11) O(2 n) exponential time Really hard problems. These grow so fast that they’re impractical 40

Examples of Each Complexity Class’s Growth Rate • From Reges/Stepp, page 708: • assume that all complexity classes can process an input of size 100 in 100 ms Input Size (n) O(1) O(log n) O(n 2) O(n 3) O(2 n) 100 ms 100 ms 200 100 ms 115 ms 200 ms 240 ms 400 ms 800 ms 32. 7 sec 400 100 ms 130 ms 400 ms 550 ms 1. 6 sec 6. 4 sec 12. 4 days 800 100 ms 145 ms 800 ms 1. 2 sec 6. 4 sec 51. 2 sec 36. 5 million years 1600 100 ms 160 ms 1. 6 sec 2. 7 sec 25. 6 sec 6 min 49. 6 sec 4. 21 * 1024 years 3200 100 ms 175 ms 3. 2 sec 6 sec 1 min 42. 4 sec 54 min 36 sec 5. 6 * 1061 years 41