CSCI256 Data Structures Algorithm Analysis Lecture 11 Note

Another Application: Collaborative Filtering • A number of sites on the Web make use

Collaborative Filtering • E. g. , Music site tries to match your song preferences

Counting Inversions • A natural method would be to label the songs (or any

Counting Inversions • Similarity metric: number of inversions between two rankings – My rank:

Inversion Problem • Let a 1, . . . an be a permutation of

Inversion Problem • We are inspired by the Mergesort – each iteration of the

Counting Inversions: Divide-and-Conquer • Divide-and-conquer – Divide: separate list into two pieces – Conquer:

Problem: how do we count inversions between sub problems in O(n) time? • Solution:

Merge-and-Count(A, B) (A, B previously sorted) Maintain a Current pointer into each list, initialized

Merge and Count Merge and count step. Given two sorted halves, count number of

Use the merge algorithm to count inversions 1 5 4 8 11 9 12

Counting Inversions: Combine • Counting inversions between two sorted lists – O(1) per element

• Since the Merge-and–Count Procedure takes O(n) time, the running time T(n) of

Counting Inversions: Implementation Sort-and-Count(L) { If list L has one element return 0 and

Slides: 40

Download presentation

Another Application: Collaborative Filtering • A number of sites on the Web make use of a technique known as collaborative filtering, in which they try to match your preferences with those of other people • Once the Web site has identified people with “similar” tastes to yours – based on a comparison of how you and they rate various things – it can recommend new things that these other people have liked

Collaborative Filtering • E. g. , Music site tries to match your song preferences with others – You rank n songs – Music site consults database to find people with similar tastes • A core issue in applications like this is the problem of comparing two rankings. How to define similarity between two rankings?

Counting Inversions • A natural method would be to label the songs (or any other objects being ranked) from 1 to n according to your ranking and then according to the other person’s rankings, and see how many pairs are “out of order”

Counting Inversions • Similarity metric: number of inversions between two rankings – My rank: 1, 2, …, n – Your rank: a 1, a 2, …, an – Songs i and j inverted if i < j, but ai > aj Songs A B C D E Me 1 2 3 4 5 You 1 3 4 2 5 Inversions 3 -2, 4 -2

Inversion Problem • Let a 1, . . . an be a permutation of 1. . n • (ai, aj) is an inversion if i < j and ai > aj 4, 6, 1, 7, 3, 2, 5 • Problem: given a permutation, count the number of inversions • Can be done easily in O(n 2) time by brute force – Can we do better?

Inversion Problem • We are inspired by the Mergesort – each iteration of the While loop takes constant time and in each iteration, we add some element to the output that will never be seen again; the number of iterations can be at most the sum of the initial lengths of A and B so the running time is O(n) • Thus we will look at a recursive algorithm Sortand-Count which has at its centre a Merge-and. Count process to merge and count the number of iterations in two sorted lists

Counting Inversions: Divide-and-Conquer • Divide-and-conquer – Divide: separate list into two pieces – Conquer: recursively count inversions in each half – Combine: count inversions where ai and aj are in different halves, and return sum of three quantities 1 1 5 5 4 4 8 8 10 10 2 2 6 6 5 blue-blue inversions 9 9 12 12 11 3 3 7 7 Divide: O(1) Conquer: 2 T(n / 2) 8 green-green inversions 9 blue-green inversions 5 -3, 4 -3, 8 -6, 8 -3, 8 -7, 10 -6, 10 -9, 10 -3, 10 -7 Total = 5 + 8 + 9 = 22 11 Combine: ? ? ?

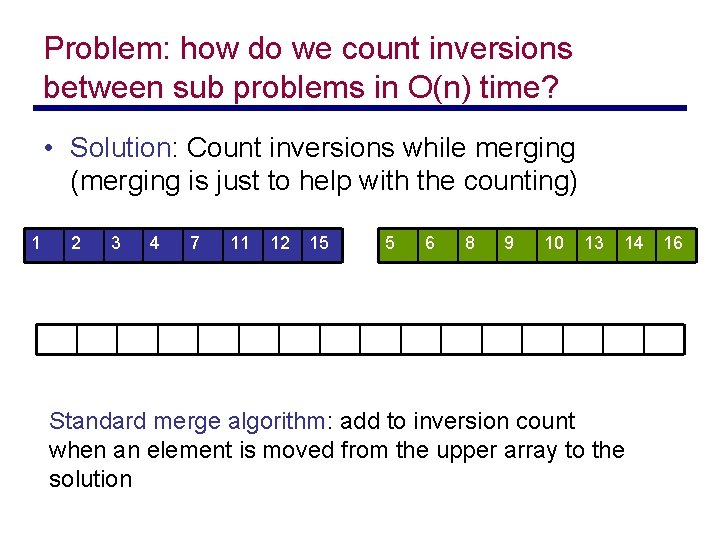
Problem: how do we count inversions between sub problems in O(n) time? • Solution: Count inversions while merging (merging is just to help with the counting) 1 2 3 4 7 11 12 15 5 6 8 9 10 13 14 Standard merge algorithm: add to inversion count when an element is moved from the upper array to the solution 16

Merge-and-Count(A, B) (A, B previously sorted) Maintain a Current pointer into each list, initialized to point to the front elements Maintain a variable Count for the number of inversions, initialized to 0 While both lists are nonempty: Let ai and bj be the elements pointed to by the Current pointer Append the smaller of these two to the output list If bj is the smaller element then Increment Count by the number of elements remaining in A Endif Advance the Current pointer in the list from which the smaller element was selected End. While Once one list is empty, append the remainder of the other list to the output Return Count and the merged list

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=6 3 7 10 14 18 19 2 11 16 17 23 25 two sorted halves auxiliary array Total:

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=5 3 7 10 14 18 19 2 11 16 17 23 25 two sorted halves 6 2 3 auxiliary array Total: 6

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=5 3 7 10 14 18 19 2 11 16 17 23 25 two sorted halves 6 2 3 7 auxiliary array Total: 6

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=4 3 7 10 14 18 19 2 11 16 17 23 25 two sorted halves 6 2 3 7 auxiliary array Total: 6

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=4 3 7 10 14 18 19 2 11 16 17 23 25 two sorted halves 6 2 3 7 10 auxiliary array Total: 6

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=3 3 7 10 14 18 19 2 11 16 17 23 25 two sorted halves 6 2 3 7 10 auxiliary array Total: 6

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=3 3 7 2 10 3 14 7 18 10 19 2 11 6 3 11 16 17 23 25 two sorted halves auxiliary array Total: 6 + 3

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=3 3 7 2 10 3 14 7 18 10 19 11 2 11 6 3 14 16 17 23 25 two sorted halves auxiliary array Total: 6 + 3

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=2 3 7 2 10 3 14 7 18 10 19 11 2 11 6 3 14 16 17 23 25 two sorted halves auxiliary array Total: 6 + 3

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=2 3 7 2 10 3 14 7 18 10 19 11 14 2 11 16 6 3 2 16 Total: 6 + 3 + 2 17 23 25 two sorted halves auxiliary array

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=2 3 7 2 10 3 14 7 18 10 19 11 14 16 2 11 16 17 6 3 2 2 17 Total: 6 + 3 + 2 23 25 two sorted halves auxiliary array

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=2 3 7 2 10 3 14 7 18 10 19 11 14 16 2 11 16 17 6 3 2 2 17 18 Total: 6 + 3 + 2 23 25 two sorted halves auxiliary array

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=1 3 7 2 10 3 14 7 18 10 19 11 14 16 2 11 16 17 6 3 2 2 17 18 Total: 6 + 3 + 2 23 25 two sorted halves auxiliary array

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=1 3 7 2 10 3 14 7 18 10 19 11 14 16 2 11 16 17 6 3 2 2 17 18 19 Total: 6 + 3 + 2 23 25 two sorted halves auxiliary array

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n first half exhausted 3 7 2 10 3 14 7 18 10 i=0 19 11 14 16 2 11 16 17 6 3 2 2 17 18 19 Total: 6 + 3 + 2 23 25 two sorted halves auxiliary array

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=0 3 7 2 10 3 14 7 18 10 19 11 14 16 2 11 16 17 23 6 3 2 2 0 17 18 19 23 Total: 6 + 3 + 2 + 0 25 two sorted halves auxiliary array

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=0 3 7 2 10 3 14 7 18 10 19 11 14 16 2 11 16 17 23 25 6 3 2 2 0 0 17 18 19 23 25 Total: 6 + 3 + 2 + 0 two sorted halves auxiliary array

Merge and Count Merge and count step. Given two sorted halves, count number of inversions where a i and aj are in different halves. Combine two sorted halves into sorted whole. n n i=0 3 7 2 10 3 14 7 18 10 19 11 14 16 2 11 16 17 23 25 6 3 2 2 0 0 17 18 19 23 25 Total: 6 + 3 + 2 + 0 = 13 two sorted halves auxiliary array

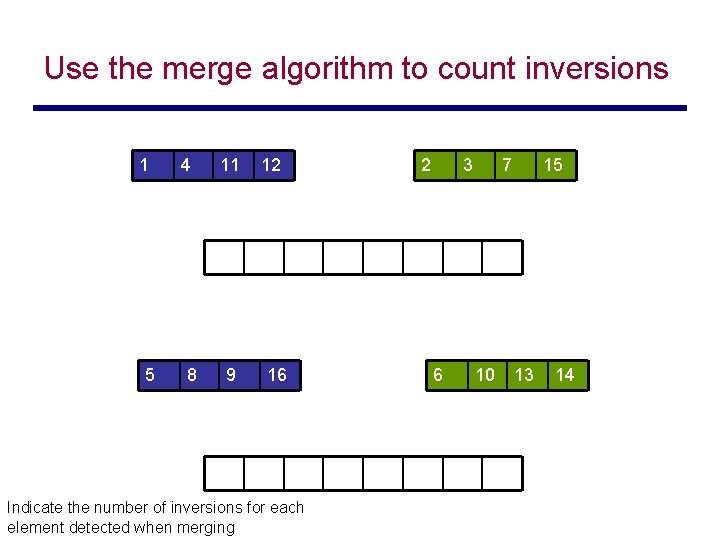
Use the merge algorithm to count inversions 1 5 4 8 11 9 12 16 Indicate the number of inversions for each element detected when merging 2 3 6 7 10 15 13 14

Counting Inversions: Combine • Counting inversions between two sorted lists – O(1) per element to count inversions x x z x z y z y z

Counting Inversions: Divide-and-Conquer • Divide-and-conquer – Divide: separate list into two pieces – Conquer: recursively count inversions in each half – Combine: count inversions where ai and aj are in different halves, and return sum of three quantities 1 1 5 5 4 4 8 8 10 10 2 2 6 6 9 9 12 12 11 11 3 3 7 7 Divide: O(1) Conquer: 2 T(n / 2) Combine: O(n)

• Since the Merge-and–Count Procedure takes O(n) time, the running time T(n) of the full Sortand-Count procedure satisfies: T(n) < 2 T(n/2) + cn 2<n and T(2) < c So running time T(n) of full Sort-and-Count is O(n log n)

Counting Inversions: Implementation Sort-and-Count(L) { If list L has one element return 0 and the list L Else Divide the list into two halves A and B (r. A, A) Sort-and-Count(A) (r. B, B) Sort-and-Count(B) (r, L) Merge-and-Count(A, B) Endif } Return r = r. A + r. B + r and the sorted list L