CSci 6971 Image Registration Lecture 9 Registration Components

CSci 6971: Image Registration Lecture 9: Registration Components February 10, 2004 Prof. Chuck Stewart, RPI Dr. Luis Ibanez, Kitware Image Registration Lecture 9

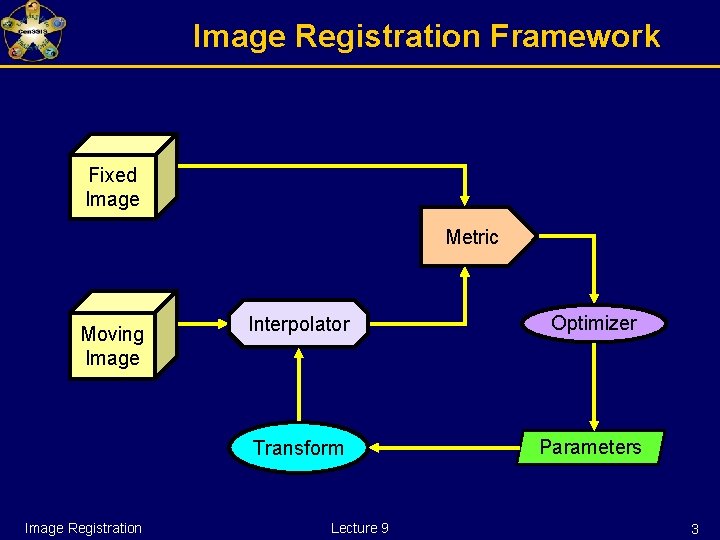
Registration Components Basic Registration Framework Image Registration Lecture 9 2

Image Registration Framework Fixed Image Metric Moving Image Registration Interpolator Optimizer Transform Parameters Lecture 9 3

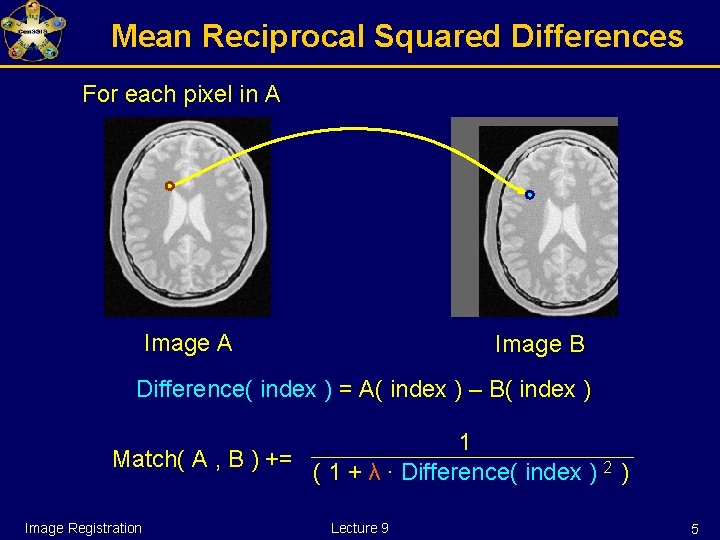
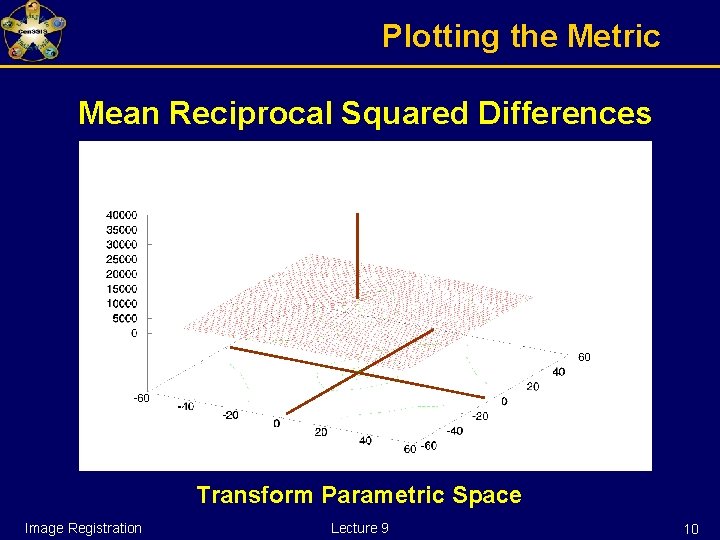
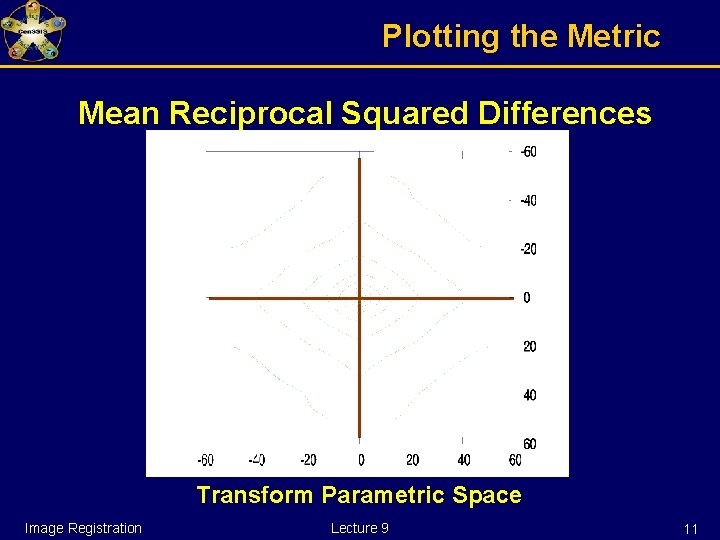
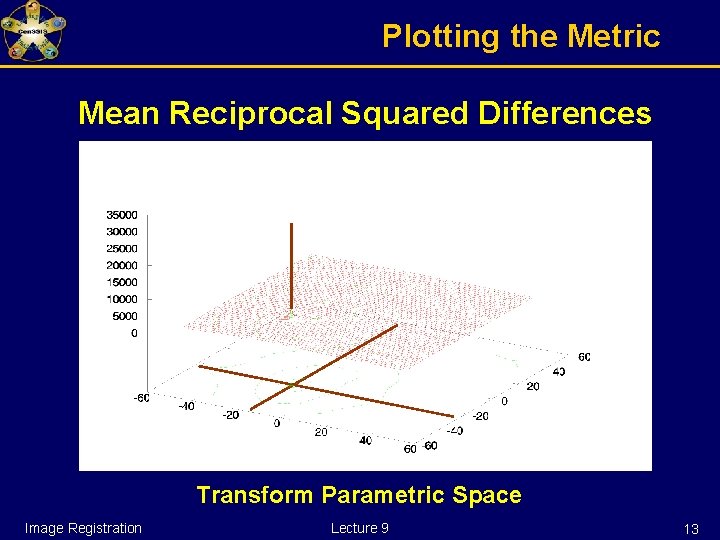
Other Image Metrics Mean Reciprocal Square Differences Image Registration Lecture 9 4

Mean Reciprocal Squared Differences For each pixel in A Image B Difference( index ) = A( index ) – B( index ) 1 Match( A , B ) += ( 1 + λ ∙ Difference( index ) 2 ) Image Registration Lecture 9 5

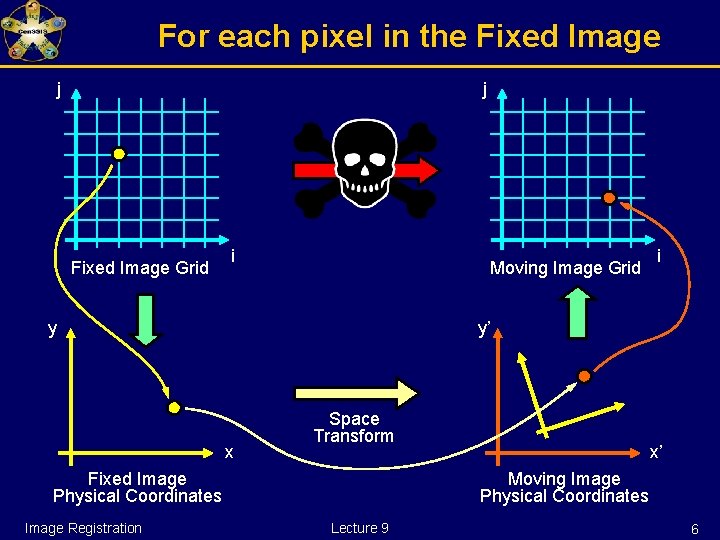
For each pixel in the Fixed Image j j Fixed Image Grid i Moving Image Grid y y’ x Space Transform Fixed Image Physical Coordinates Image Registration i x’ Moving Image Physical Coordinates Lecture 9 6

Mean Reciprocal Squared Differences #include "itk. Image. h" "itk. Mean. Reciprocal. Square. Difference. Image. To. Image. Metric. h" "itk. Linear. Interpolate. Image. Function. h" "itk. Translation. Transform. h" typedef itk: : Image< char, 2 > Image. Type; Image. Type: : Const. Pointer fixed. Image = Get. Fixed. Image(); Image. Type: : Const. Pointer moving. Image = Get. Moving. Image(); typedef itk: : Linear. Interpolate. Image. Function< Image. Type, double > Interpolator. Type; Interpolator. Type: : Pointerpolator = Interpolator. Type: : New(); typedef itk: : Translation. Transform< double, 2 > Transform. Type; Transform. Type: : Pointer transform = Transform. Type: : New(); Image Registration Lecture 9 7

Mean Reciprocal Squared Differences typedef itk: : Mean. Reciprocal. Square. Difference. Image. To. Image. Metric< Image. Type, Image. Type > Metric. Type; Metric. Type: : Pointer metric = Metric. Type: : New(); metric->Set. Interpolator( interpolator ); metric->Set. Transform( transform ); metric->Set. Fixed. Image( fixed. Image ); metric->Set. Moving. Image( moving. Image ); Metric. Type: : Transform. Parameters. Type translation( Dimension ); translation[0] = 12; translation[1] = 27; double value = metric->Get. Value( translation ); Image Registration Lecture 9 8

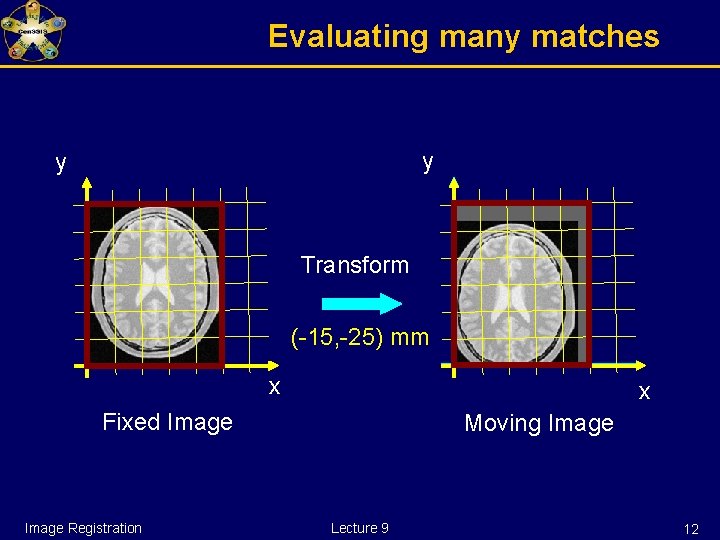
Evaluating many matches y y Transform x x Fixed Image Registration Moving Image Lecture 9 9

Plotting the Metric Mean Reciprocal Squared Differences Transform Parametric Space Image Registration Lecture 9 10

Plotting the Metric Mean Reciprocal Squared Differences Transform Parametric Space Image Registration Lecture 9 11

Evaluating many matches y y Transform (-15, -25) mm x x Fixed Image Registration Moving Image Lecture 9 12

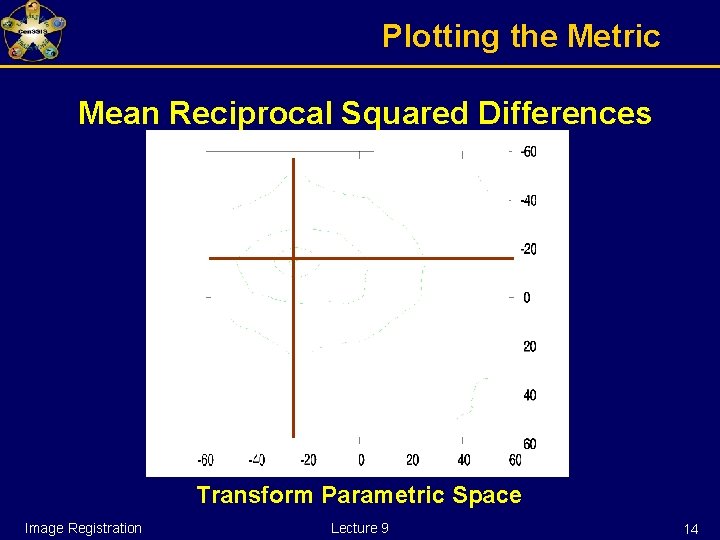
Plotting the Metric Mean Reciprocal Squared Differences Transform Parametric Space Image Registration Lecture 9 13

Plotting the Metric Mean Reciprocal Squared Differences Transform Parametric Space Image Registration Lecture 9 14

Watch over your optimizer Example: Optimizer registering an image with itself starting at (-15 mm, -25 mm) Image Registration Lecture 9 15

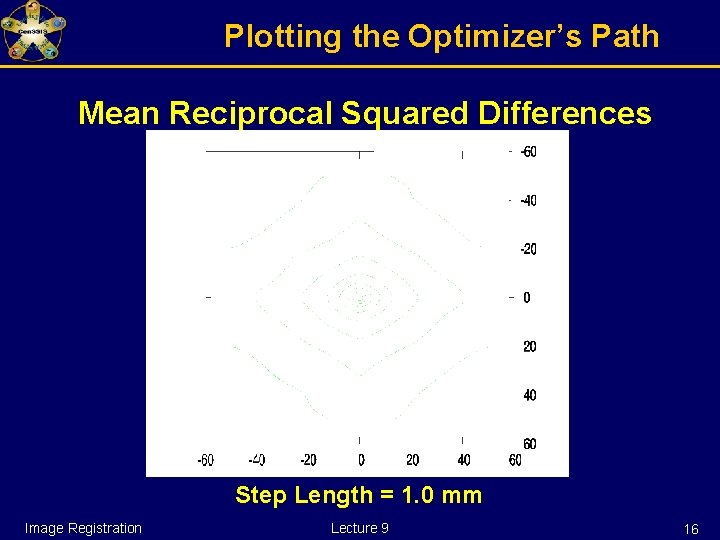
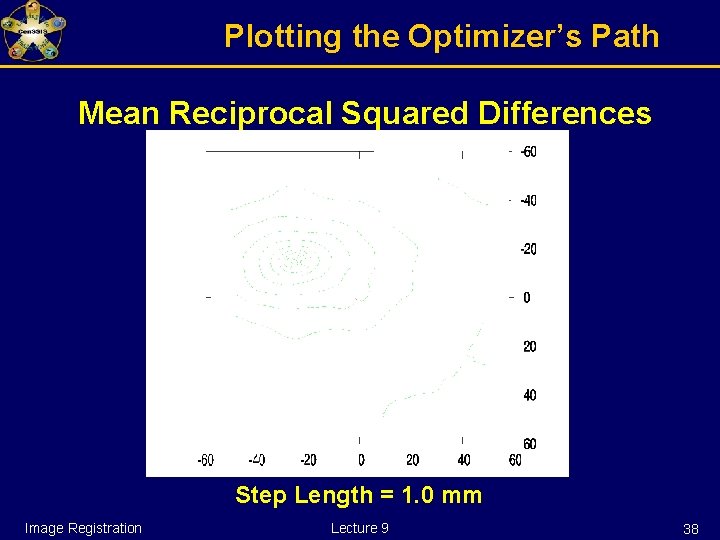
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 1. 0 mm Image Registration Lecture 9 16

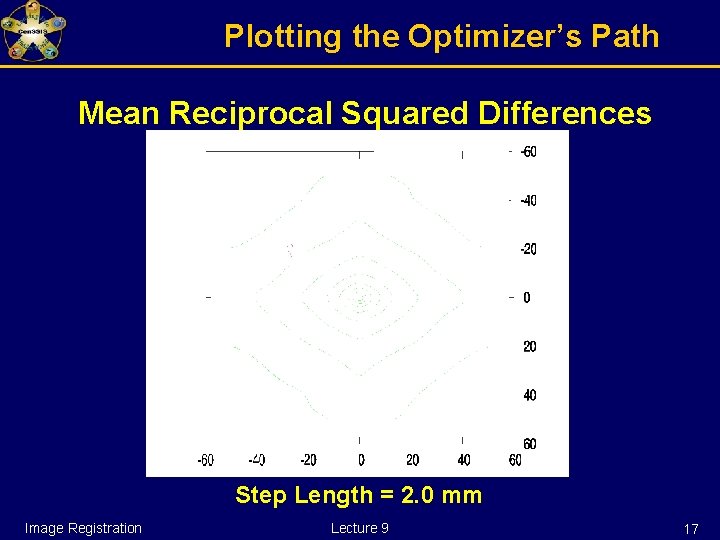
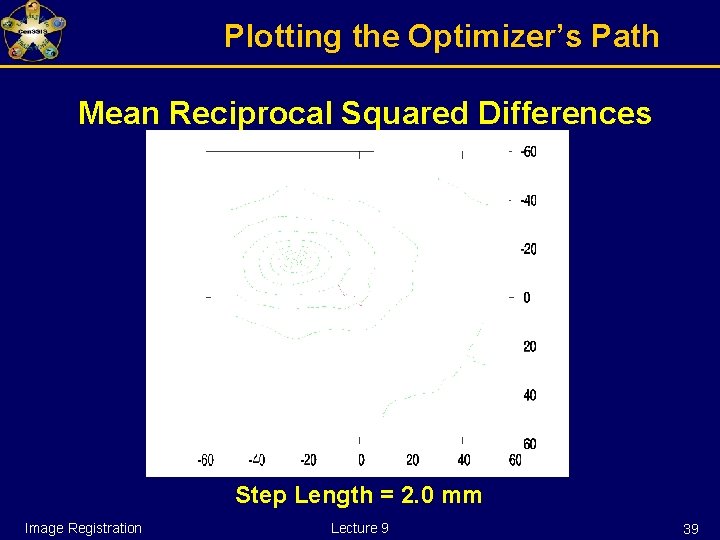
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 2. 0 mm Image Registration Lecture 9 17

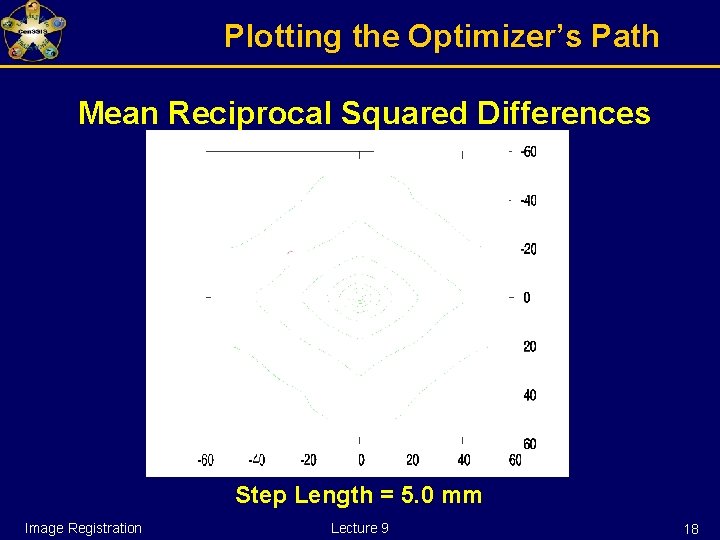
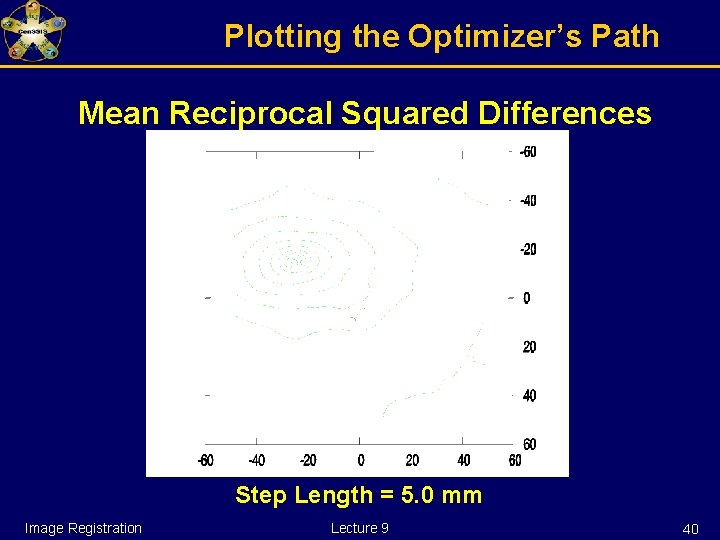
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 5. 0 mm Image Registration Lecture 9 18

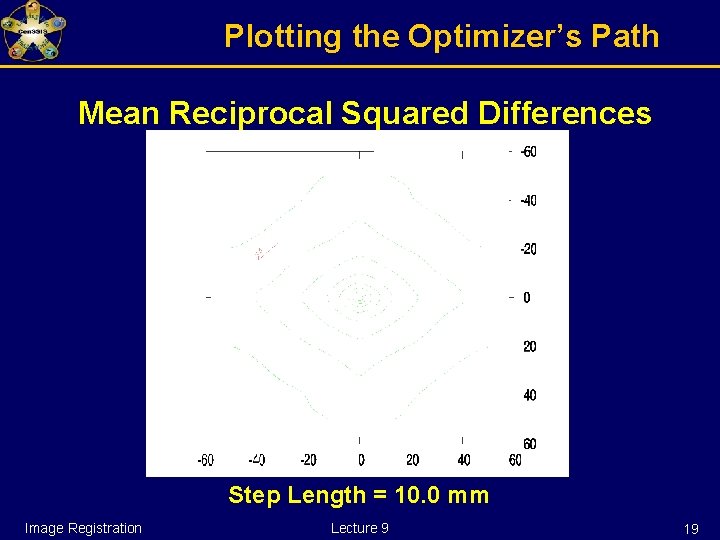
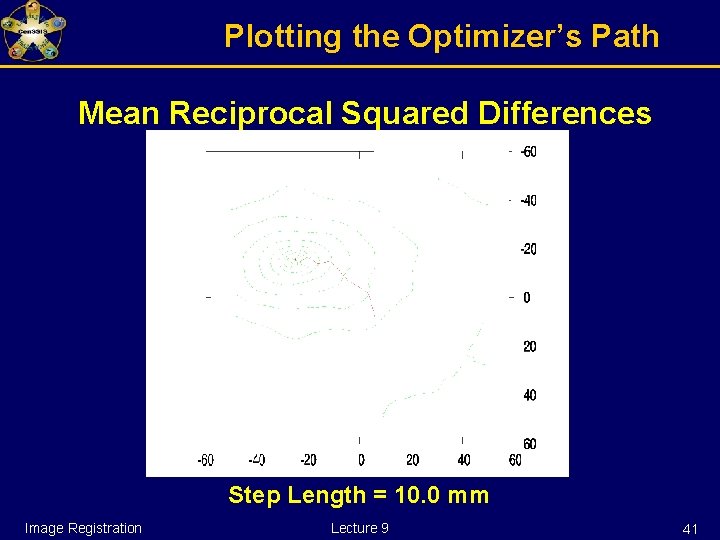
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 10. 0 mm Image Registration Lecture 9 19

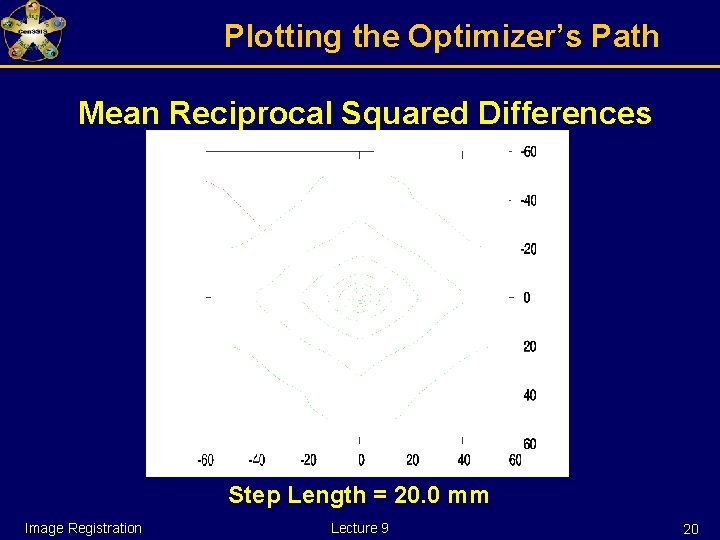
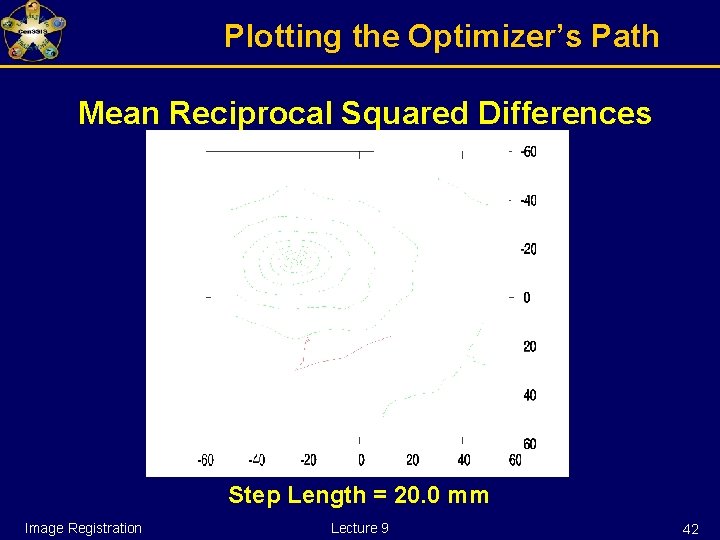
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 20. 0 mm Image Registration Lecture 9 20

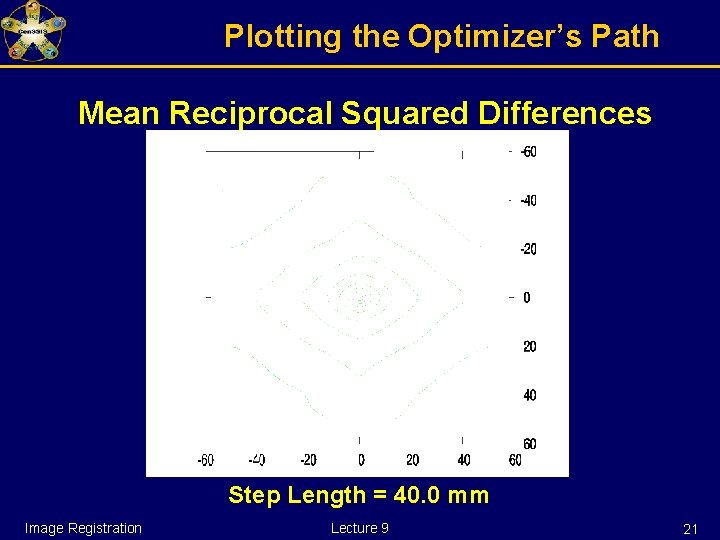
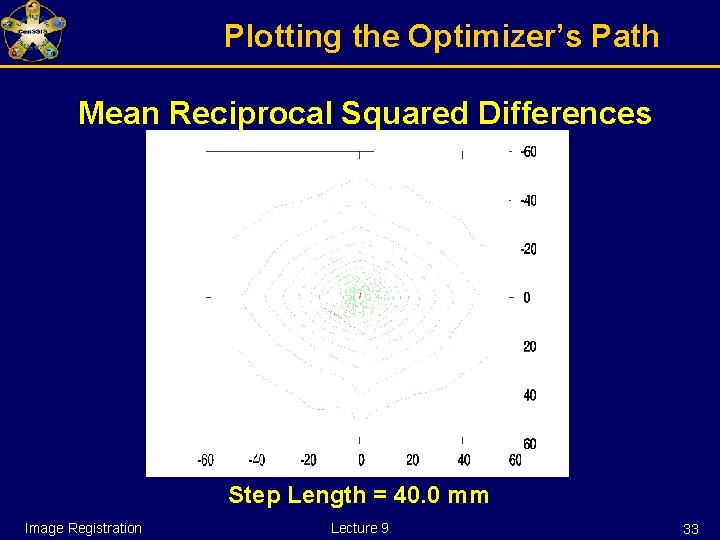
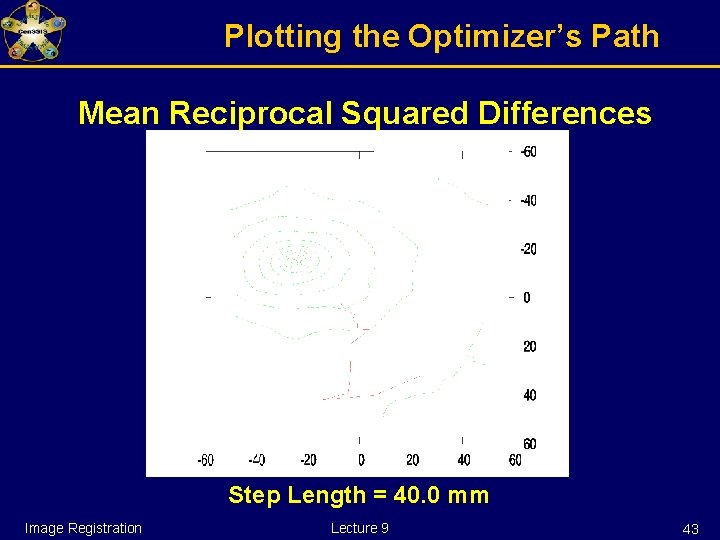
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 40. 0 mm Image Registration Lecture 9 21

Quiz #1 If the Metric is Noisy Where is the noise coming from ? Image Registration Lecture 9 22

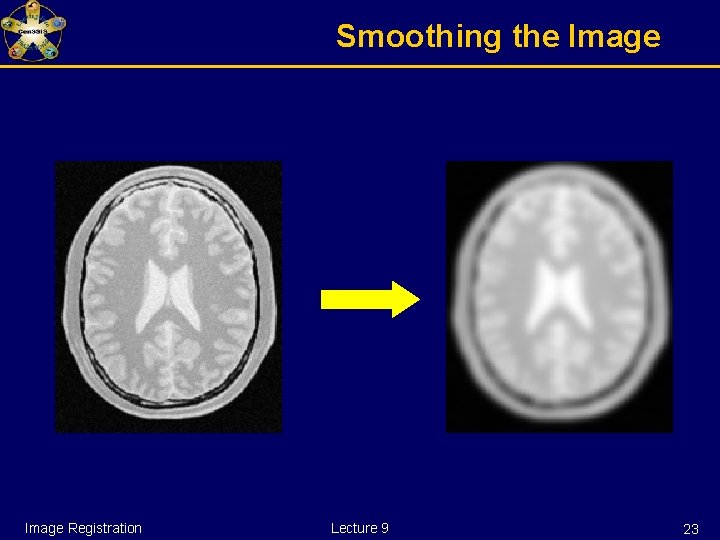
Smoothing the Image Registration Lecture 9 23

Evaluating many matches y y Transform x x Fixed Image Registration Moving Image Lecture 9 24

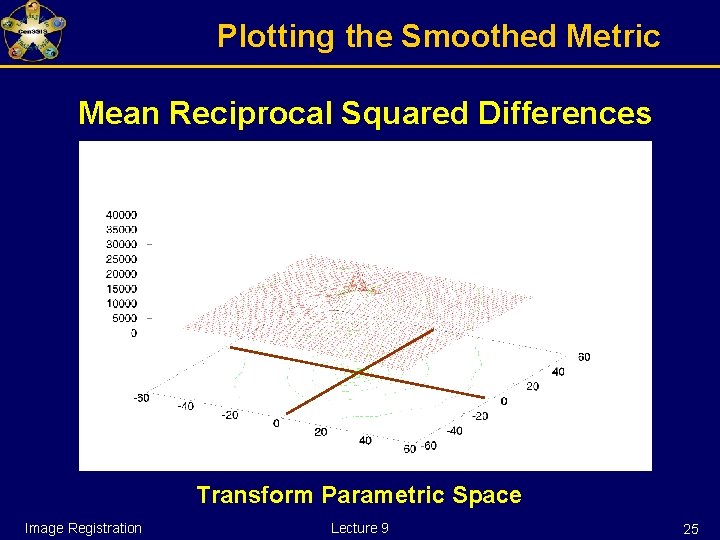
Plotting the Smoothed Metric Mean Reciprocal Squared Differences Transform Parametric Space Image Registration Lecture 9 25

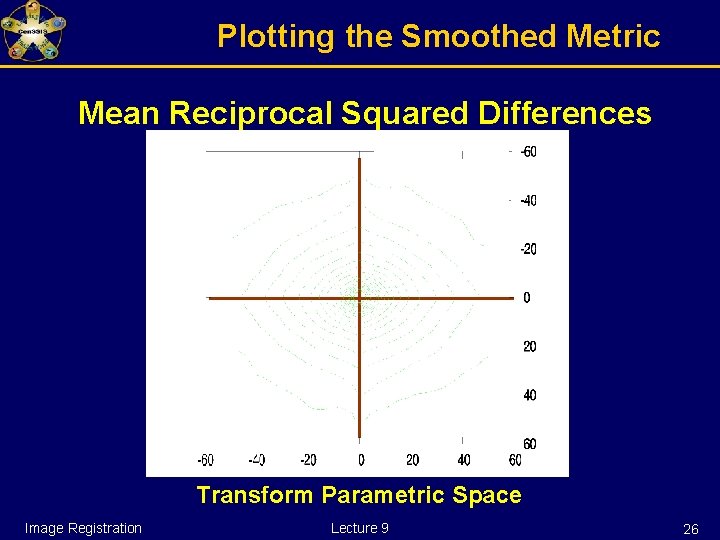
Plotting the Smoothed Metric Mean Reciprocal Squared Differences Transform Parametric Space Image Registration Lecture 9 26

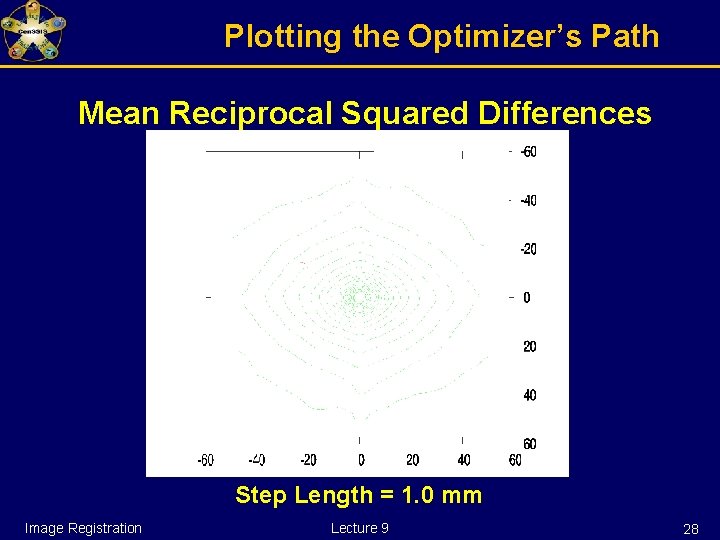
Watch over your optimizer Example: Optimizer registering an image with itself starting at (-15 mm, -25 mm) Image Registration Lecture 9 27

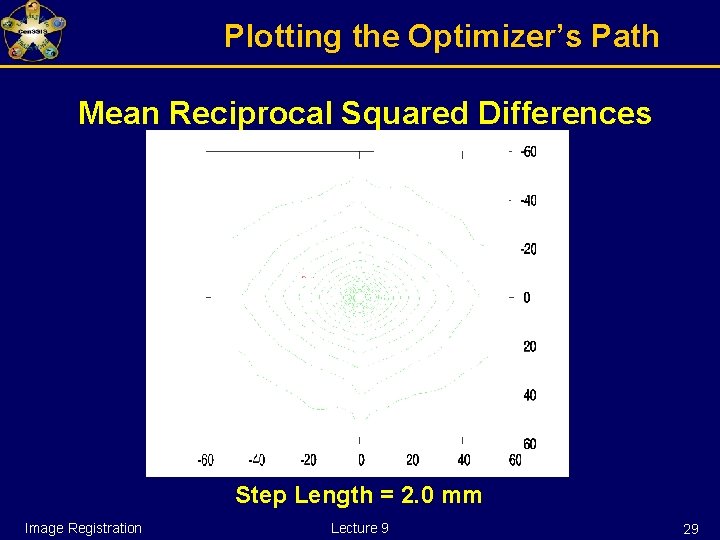
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 1. 0 mm Image Registration Lecture 9 28

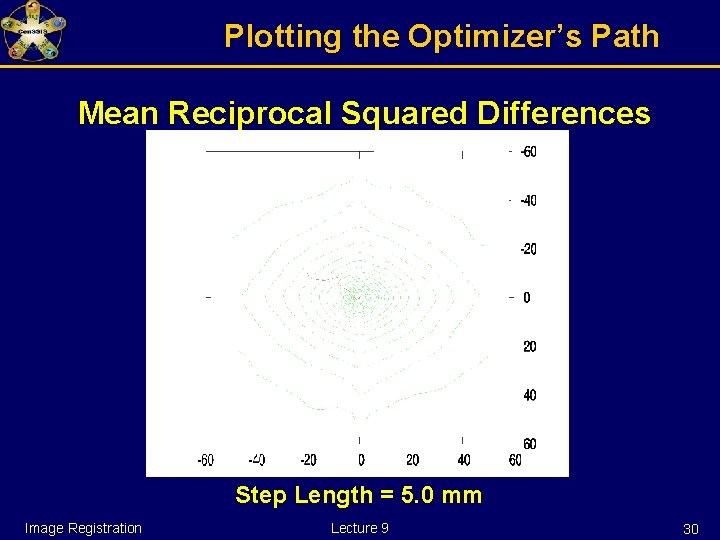
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 2. 0 mm Image Registration Lecture 9 29

Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 5. 0 mm Image Registration Lecture 9 30

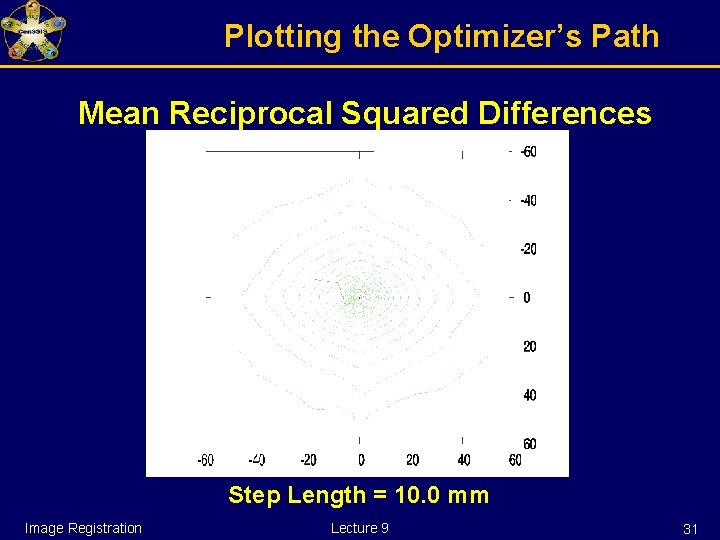
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 10. 0 mm Image Registration Lecture 9 31

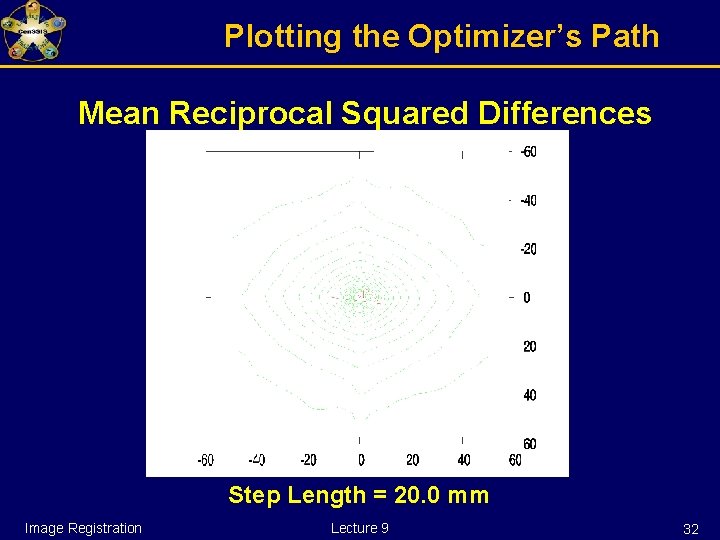
Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 20. 0 mm Image Registration Lecture 9 32

Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 40. 0 mm Image Registration Lecture 9 33

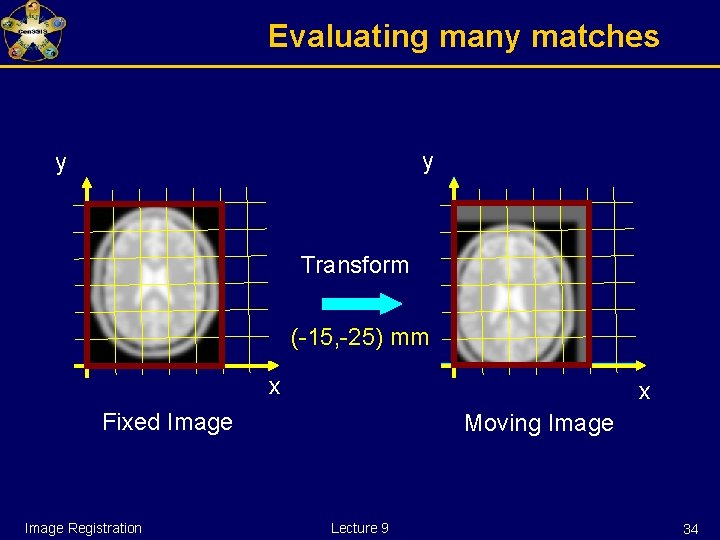
Evaluating many matches y y Transform (-15, -25) mm x x Fixed Image Registration Moving Image Lecture 9 34

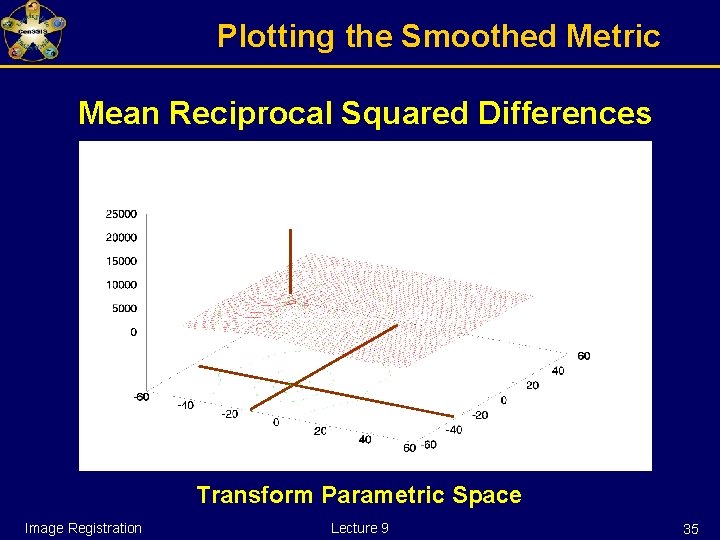
Plotting the Smoothed Metric Mean Reciprocal Squared Differences Transform Parametric Space Image Registration Lecture 9 35

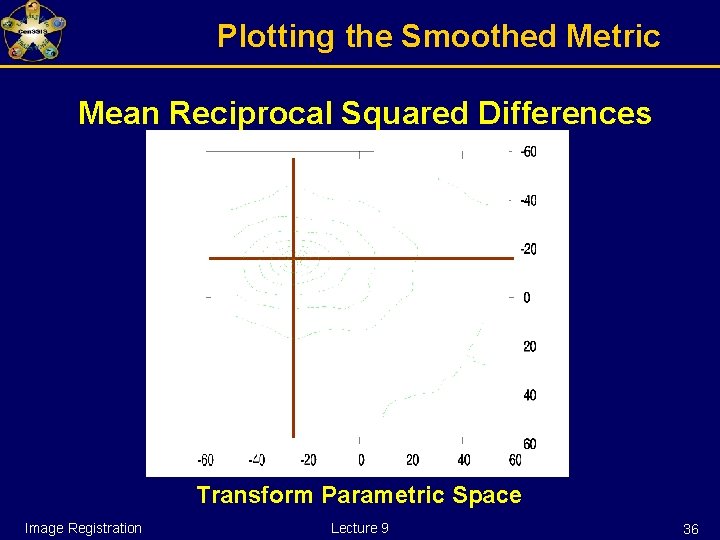
Plotting the Smoothed Metric Mean Reciprocal Squared Differences Transform Parametric Space Image Registration Lecture 9 36

Watch over your optimizer Example: Optimizer registering an image shifted by (-15 mm, -25 mm) The optimizer starts at (0 mm, 0 mm) Image Registration Lecture 9 37

Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 1. 0 mm Image Registration Lecture 9 38

Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 2. 0 mm Image Registration Lecture 9 39

Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 5. 0 mm Image Registration Lecture 9 40

Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 10. 0 mm Image Registration Lecture 9 41

Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 20. 0 mm Image Registration Lecture 9 42

Plotting the Optimizer’s Path Mean Reciprocal Squared Differences Step Length = 40. 0 mm Image Registration Lecture 9 43

Other Image Metrics Multi – Modality Registration Image Registration Lecture 9 44

Multiple Image Modalities Number of pairs Image Registration Lecture 9 45

Multiple Image Modalities More possible pairs Image Registration Lecture 9 46

Intuitive Notion of Joint Entropy The More Pairs Exist The Larger the Joint Entropy Image Registration Lecture 9 47

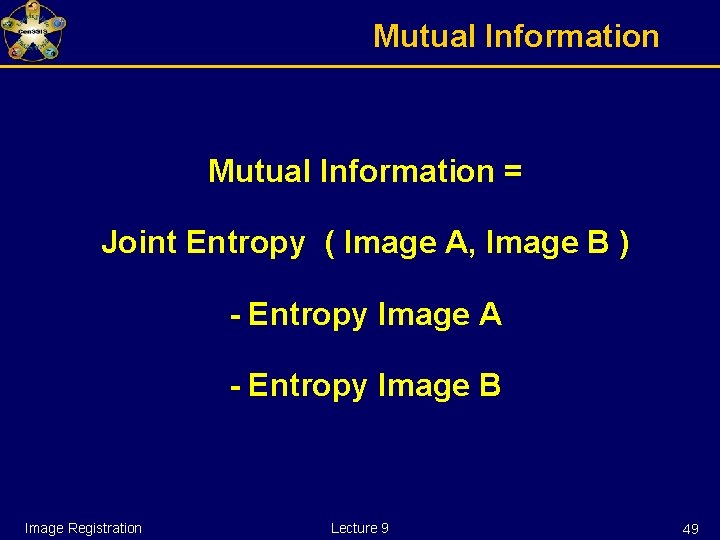
Mutual Information Reduction of Number of Pairs Reduction of Joint Entropy Image Registration Lecture 9 48

Mutual Information = Joint Entropy ( Image A, Image B ) - Entropy Image A - Entropy Image B Image Registration Lecture 9 49

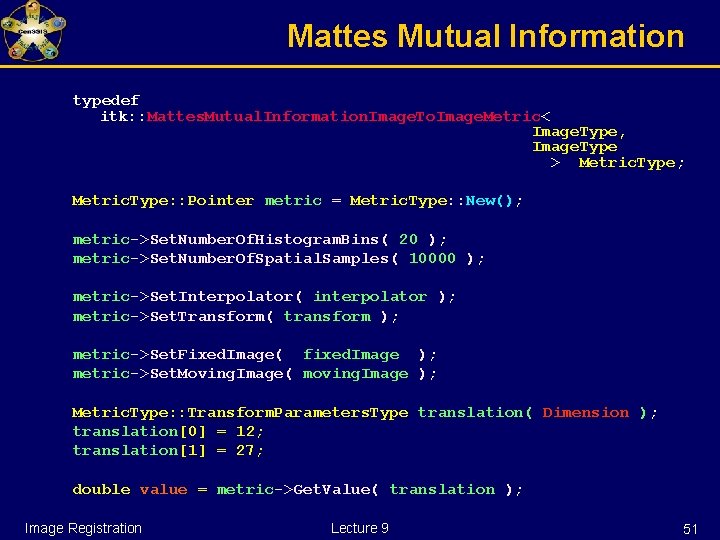
Mattes Mutual Information #include "itk. Image. h" "itk. Mattes. Mutual. Information. Image. To. Image. Metric. h" "itk. Linear. Interpolate. Image. Function. h" "itk. Translation. Transform. h" typedef itk: : Image< char, 2 > Image. Type; Image. Type: : Const. Pointer fixed. Image = Get. Fixed. Image(); Image. Type: : Const. Pointer moving. Image = Get. Moving. Image(); typedef itk: : Linear. Interpolate. Image. Function< Image. Type, double > Interpolator. Type; Interpolator. Type: : Pointerpolator = Interpolator. Type: : New(); typedef itk: : Translation. Transform< double, 2 > Transform. Type; Transform. Type: : Pointer transform = Transform. Type: : New(); Image Registration Lecture 9 50

Mattes Mutual Information typedef itk: : Mattes. Mutual. Information. Image. To. Image. Metric< Image. Type, Image. Type > Metric. Type; Metric. Type: : Pointer metric = Metric. Type: : New(); metric->Set. Number. Of. Histogram. Bins( 20 ); metric->Set. Number. Of. Spatial. Samples( 10000 ); metric->Set. Interpolator( interpolator ); metric->Set. Transform( transform ); metric->Set. Fixed. Image( fixed. Image ); metric->Set. Moving. Image( moving. Image ); Metric. Type: : Transform. Parameters. Type translation( Dimension ); translation[0] = 12; translation[1] = 27; double value = metric->Get. Value( translation ); Image Registration Lecture 9 51

Evaluating many matches y y Transform x x Fixed Image Registration Moving Image Lecture 9 52

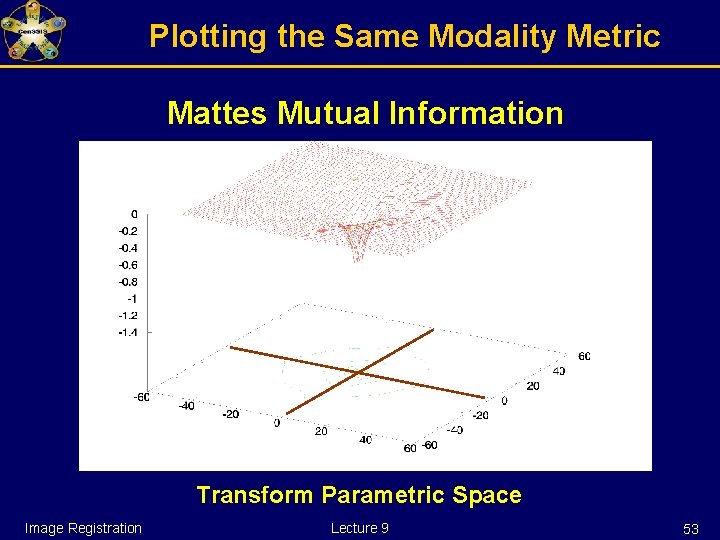
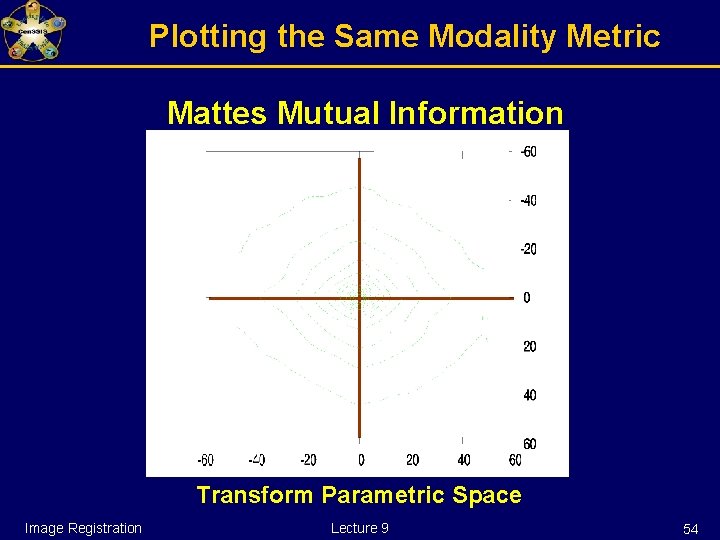
Plotting the Same Modality Metric Mattes Mutual Information Transform Parametric Space Image Registration Lecture 9 53

Plotting the Same Modality Metric Mattes Mutual Information Transform Parametric Space Image Registration Lecture 9 54

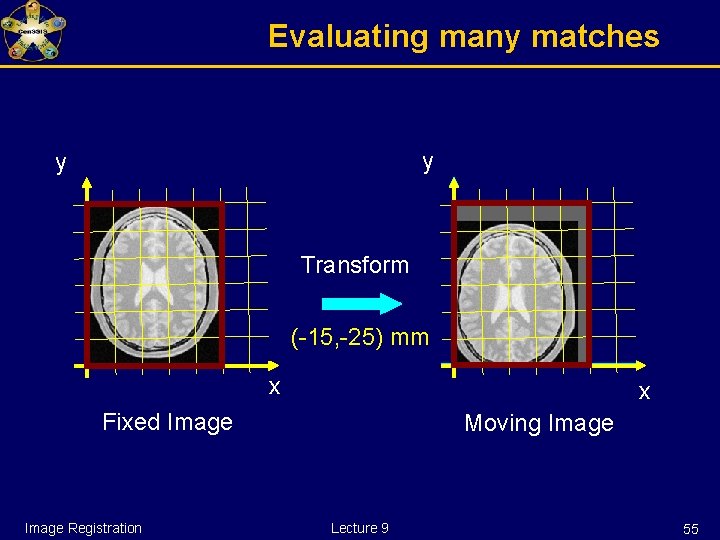
Evaluating many matches y y Transform (-15, -25) mm x x Fixed Image Registration Moving Image Lecture 9 55

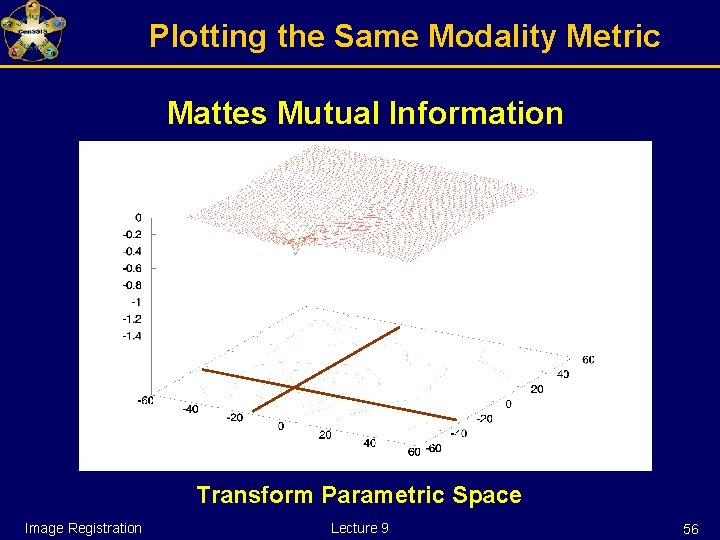
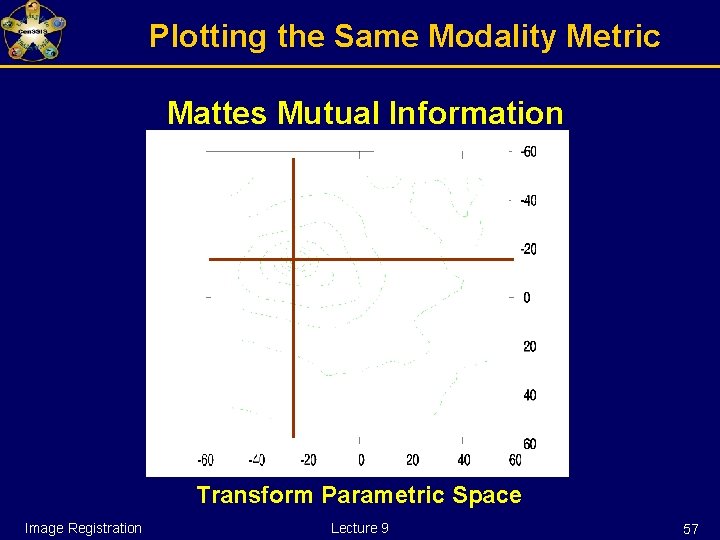
Plotting the Same Modality Metric Mattes Mutual Information Transform Parametric Space Image Registration Lecture 9 56

Plotting the Same Modality Metric Mattes Mutual Information Transform Parametric Space Image Registration Lecture 9 57

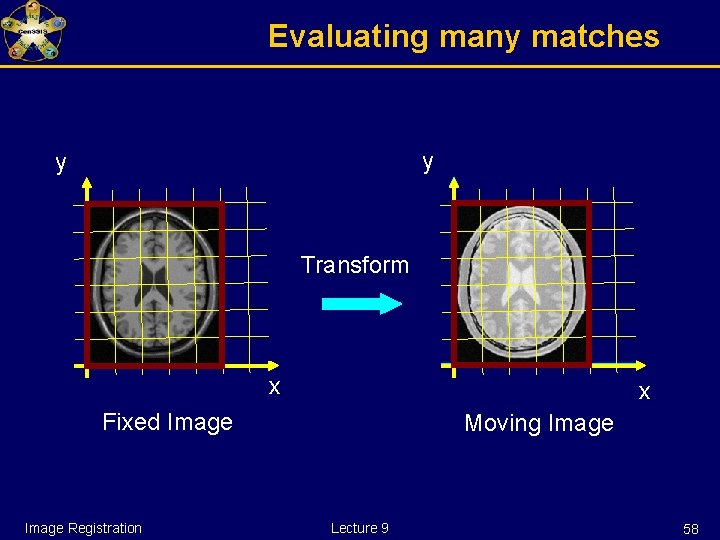
Evaluating many matches y y Transform x x Fixed Image Registration Moving Image Lecture 9 58

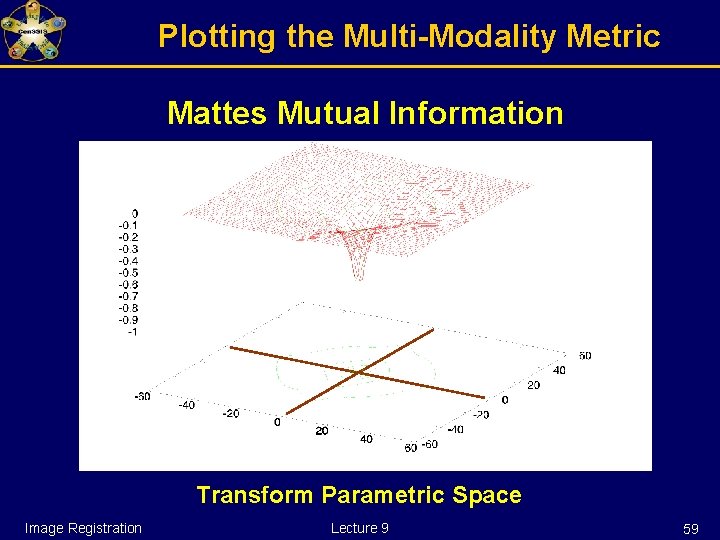
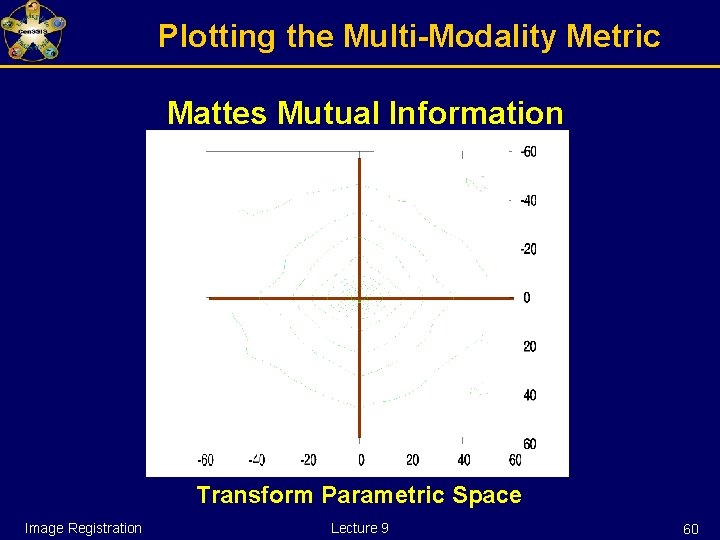
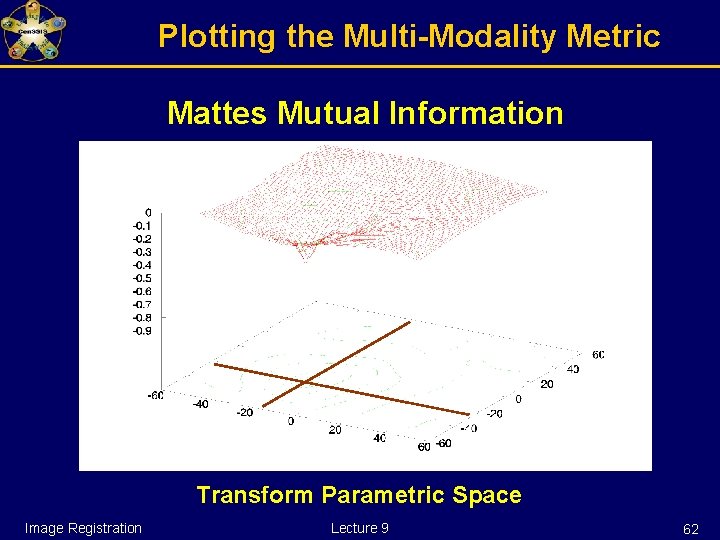
Plotting the Multi-Modality Metric Mattes Mutual Information Transform Parametric Space Image Registration Lecture 9 59

Plotting the Multi-Modality Metric Mattes Mutual Information Transform Parametric Space Image Registration Lecture 9 60

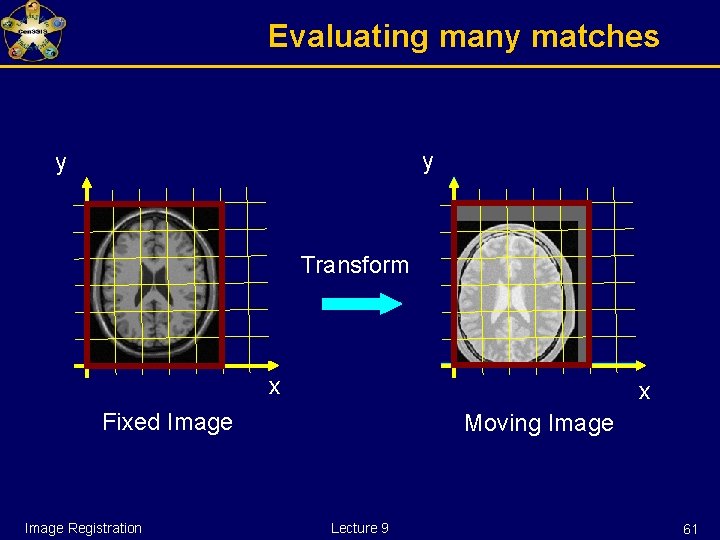
Evaluating many matches y y Transform x x Fixed Image Registration Moving Image Lecture 9 61

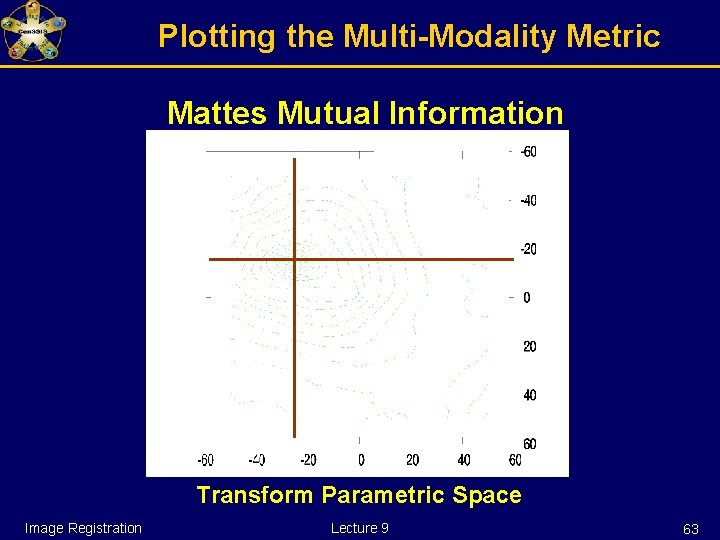
Plotting the Multi-Modality Metric Mattes Mutual Information Transform Parametric Space Image Registration Lecture 9 62

Plotting the Multi-Modality Metric Mattes Mutual Information Transform Parametric Space Image Registration Lecture 9 63

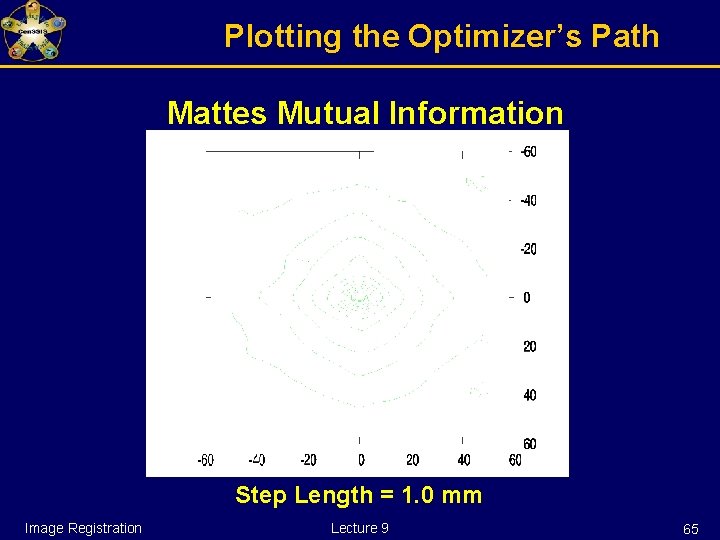
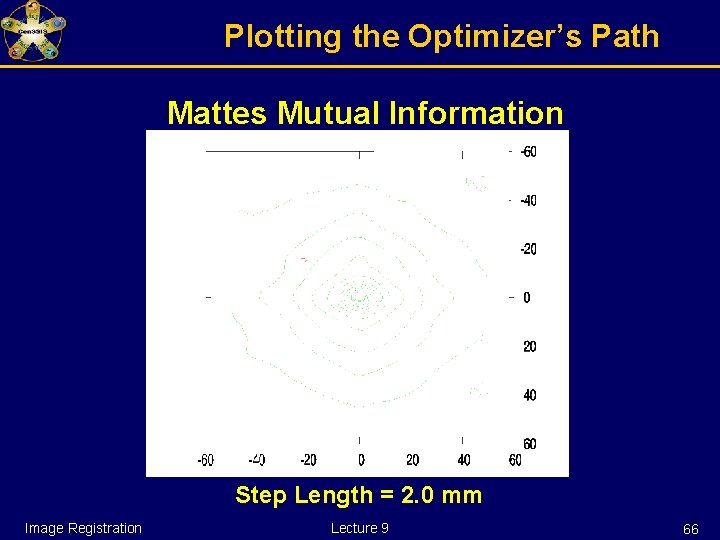
Watch over your optimizer Example: Optimizer registering two aligned multi-modality images starting at (-15 mm, -25 mm) Image Registration Lecture 9 64

Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 1. 0 mm Image Registration Lecture 9 65

Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 2. 0 mm Image Registration Lecture 9 66

Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 5. 0 mm Image Registration Lecture 9 67

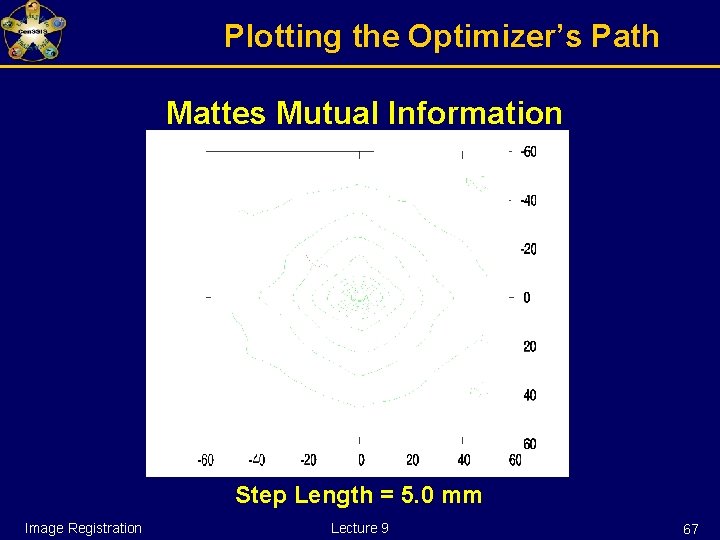
Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 10. 0 mm Image Registration Lecture 9 68

Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 20. 0 mm Image Registration Lecture 9 69

Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 40. 0 mm Image Registration Lecture 9 70

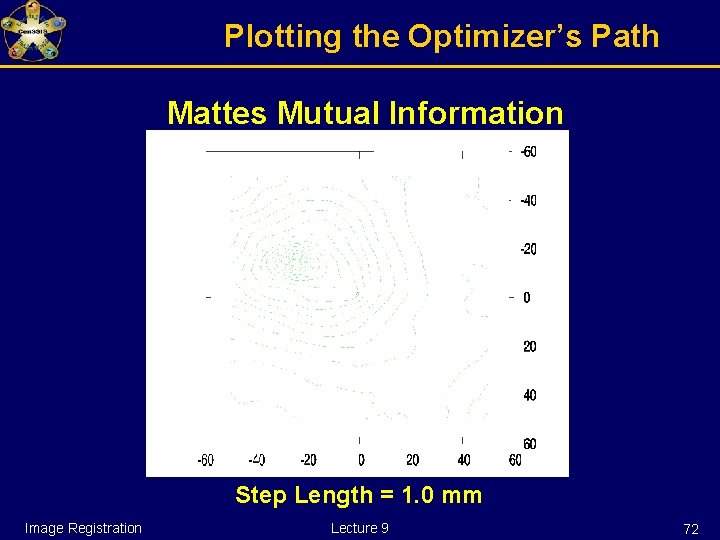
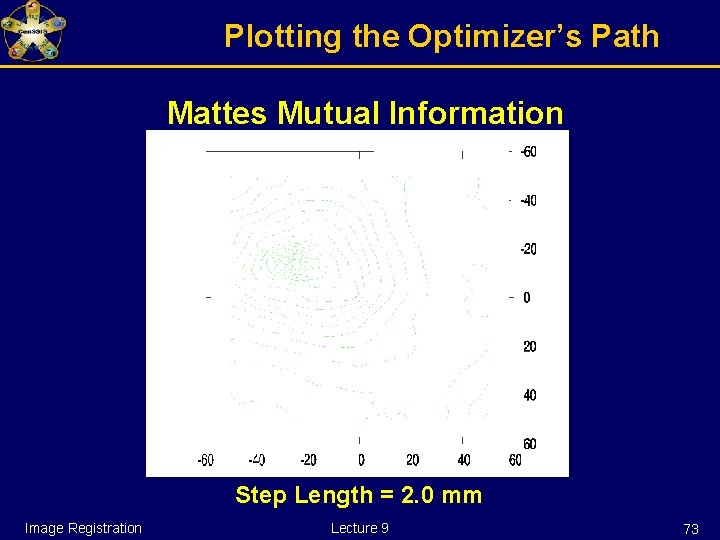
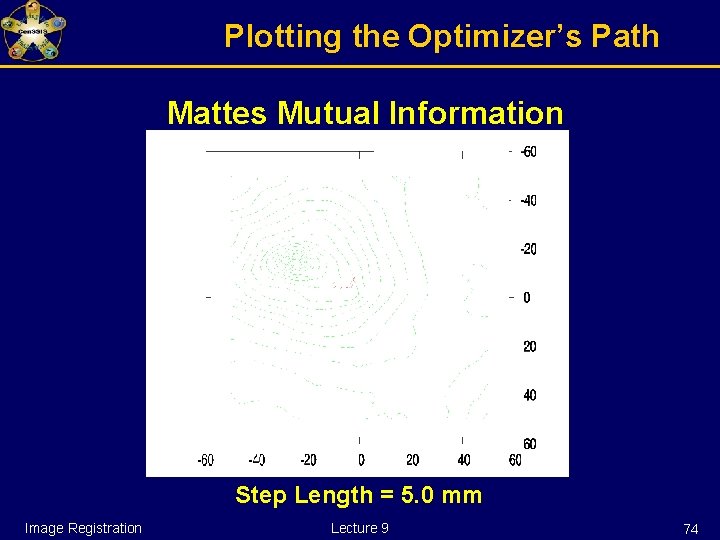
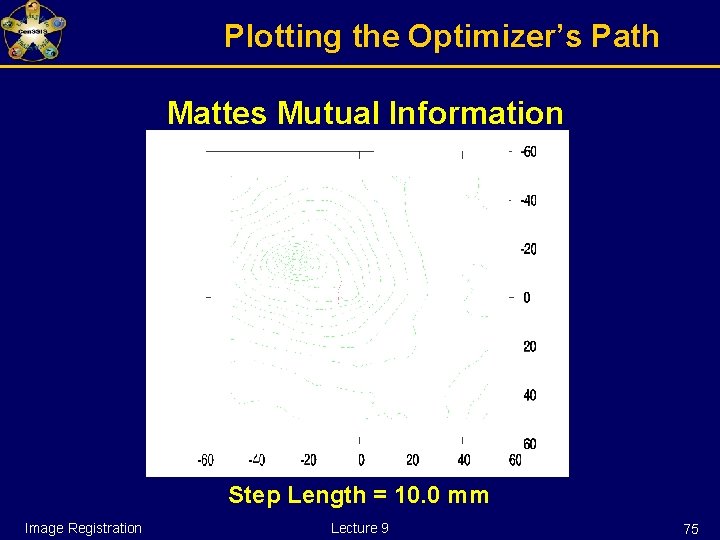
Watch over your optimizer Example: Optimizer registering two multi-modality images shifted by (-15 mm, -25 mm) The optimizer starts at (0 mm, 0 mm) Image Registration Lecture 9 71

Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 1. 0 mm Image Registration Lecture 9 72

Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 2. 0 mm Image Registration Lecture 9 73

Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 5. 0 mm Image Registration Lecture 9 74

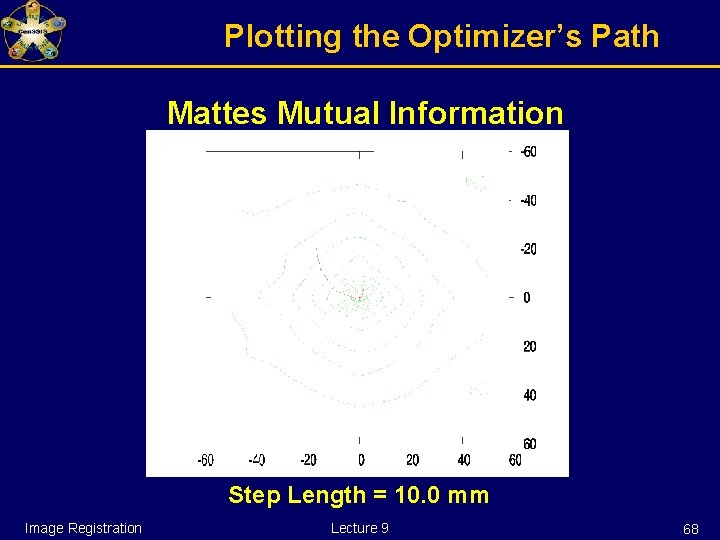
Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 10. 0 mm Image Registration Lecture 9 75

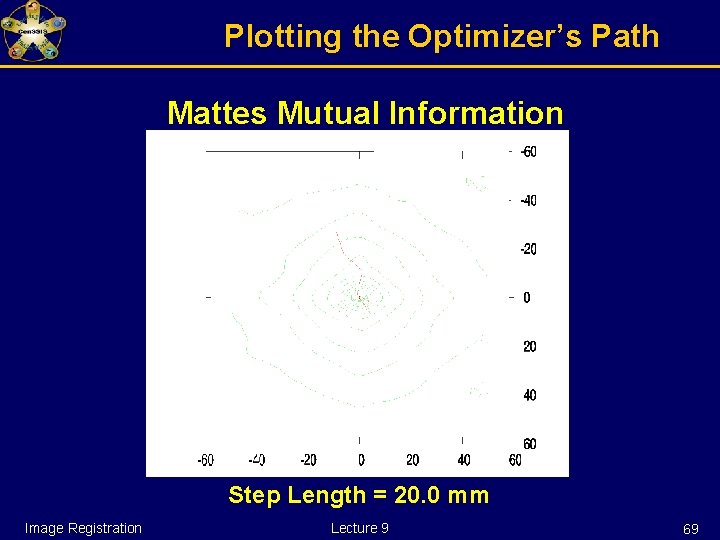
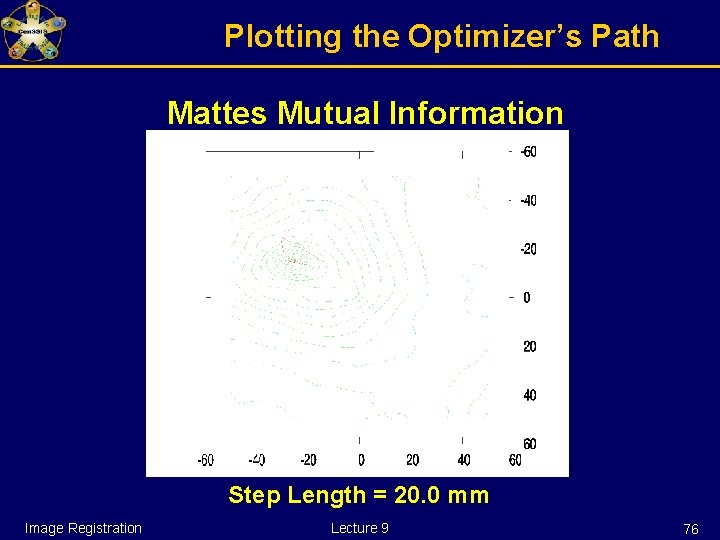
Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 20. 0 mm Image Registration Lecture 9 76

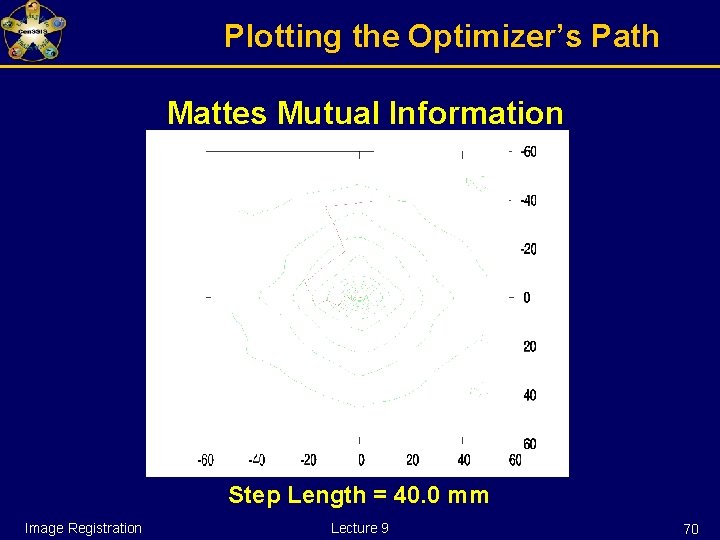
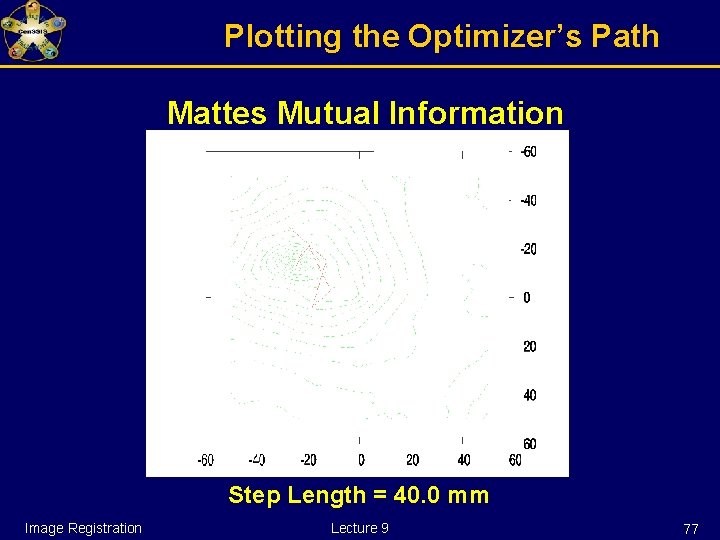
Plotting the Optimizer’s Path Mattes Mutual Information Step Length = 40. 0 mm Image Registration Lecture 9 77

Mutual Information Variants in ITK • Viola – Wells • Mattes • Mutual Information Histogram Image Registration Lecture 9 78

End Enjoy ITK ! Image Registration Lecture 9 79