CSCI 3333 Data Structures Trees Acknowledgement Dr Bun

CSCI 3333 Data Structures Trees

Acknowledgement Dr. Bun Yue ¡ Mr. Charles Moen ¡ Dr. Wei Ding ¡ Ms. Krishani Abeysekera ¡ Dr. Michael Goodrich ¡ Dr. Richard F. Gilberg ¡

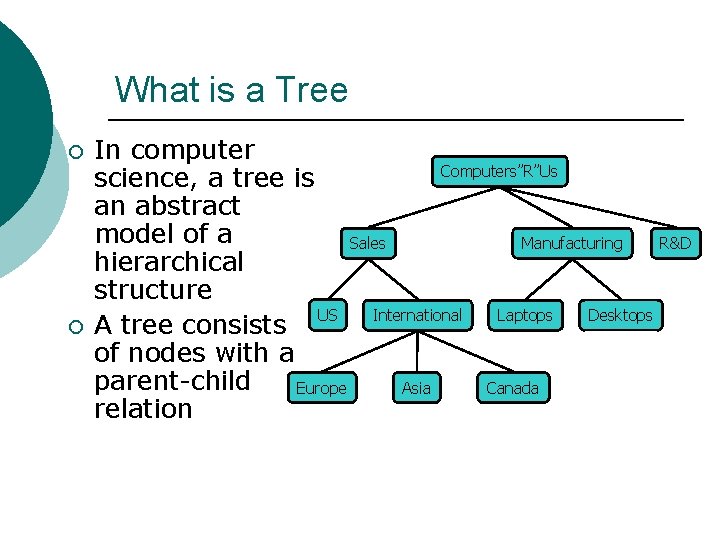
What is a Tree ¡ ¡ In computer Computers”R”Us science, a tree is an abstract model of a Sales Manufacturing R&D hierarchical structure A tree consists US International Laptops Desktops of nodes with a parent-child Europe Asia Canada relation

Some Tree Applications ¡ Applications: l l Organization charts File Folders Email Repository Programming environments: e. g. drop down menus.

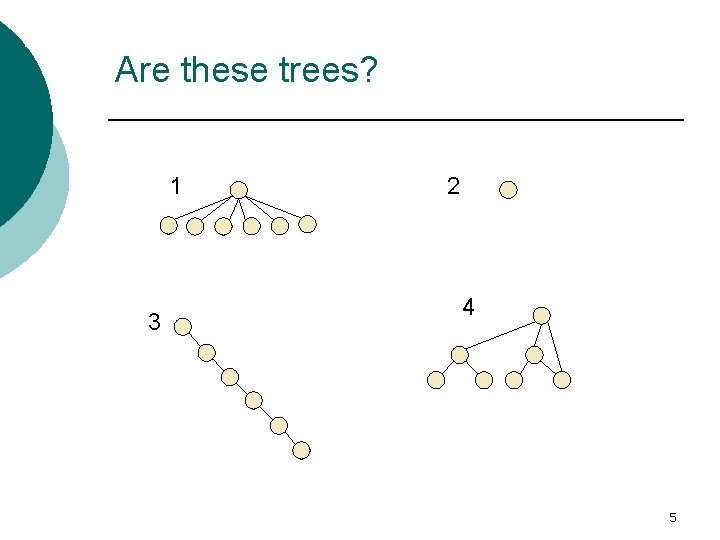
Trees Are these trees? 1 3 2 4 5

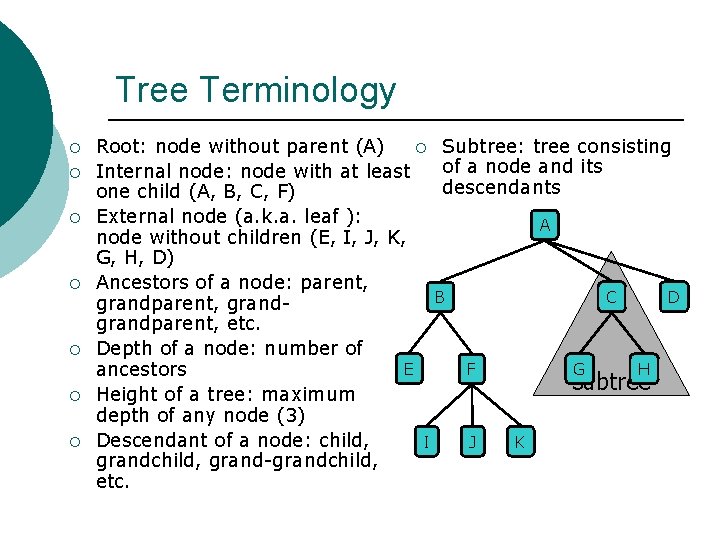
Tree Terminology ¡ ¡ ¡ ¡ Root: node without parent (A) ¡ Internal node: node with at least one child (A, B, C, F) External node (a. k. a. leaf ): node without children (E, I, J, K, G, H, D) Ancestors of a node: parent, grandgrandparent, etc. Depth of a node: number of E ancestors Height of a tree: maximum depth of any node (3) Descendant of a node: child, I grandchild, grand-grandchild, etc. Subtree: tree consisting of a node and its descendants A B C F J G D H subtree K

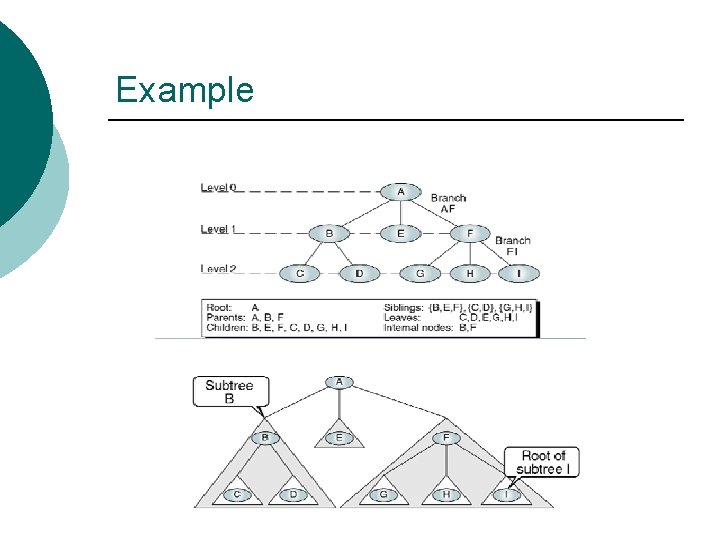
Example

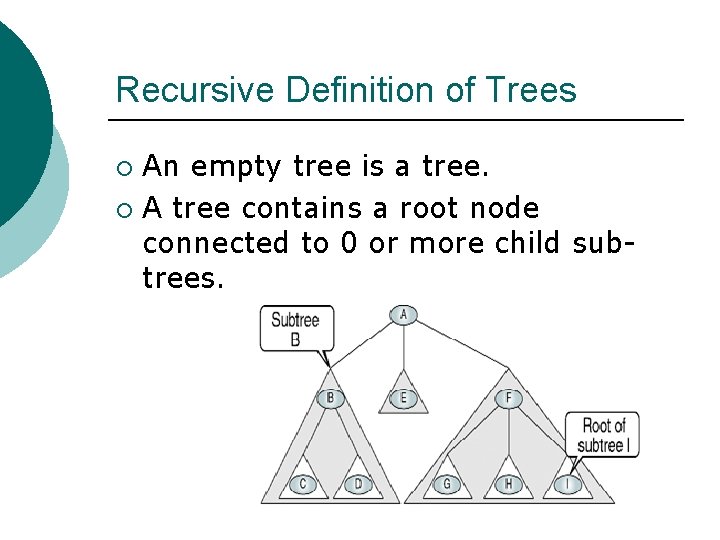
Recursive Definition of Trees An empty tree is a tree. ¡ A tree contains a root node connected to 0 or more child subtrees. ¡

Tree ADT (§ 6. 1. 2) ¡ ¡ We use positions to abstract nodes Generic methods: l l ¡ integer size() boolean is. Empty() Iterator elements() Iterator positions() Accessor methods: l l l position root() position parent(p) position. Iterator children(p) ¡ Query methods: l l l ¡ Update method: l ¡ boolean is. Internal(p) boolean is. External(p) boolean is. Root(p) object replace (p, o) Additional update methods may be defined by data structures implementing the Tree ADT

Tree Traversal Traversing is the systematic way of accessing, or ‘visiting’ all the nodes in a tree. ¡ Consider the three operations on a binary tree: ¡ l l l V: Visit a node L: (Recursively) traverse the left subtree of a node R: (Recursively) traverse the right subtree of a node

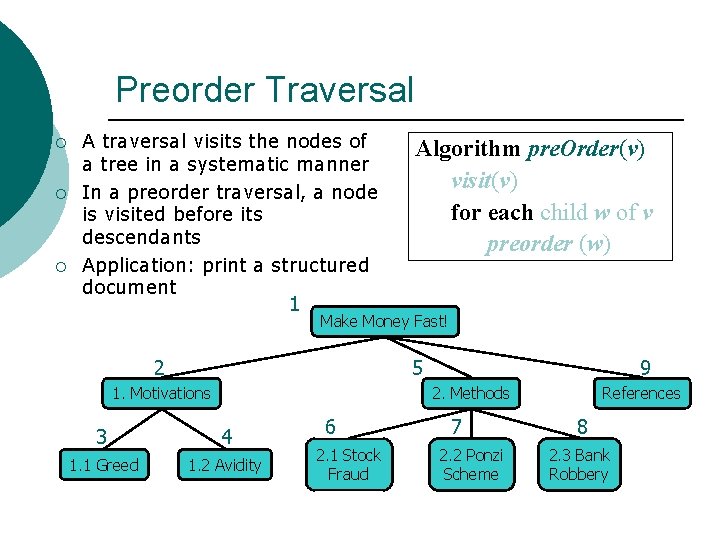
Preorder Traversal ¡ ¡ ¡ A traversal visits the nodes of a tree in a systematic manner In a preorder traversal, a node is visited before its descendants Application: print a structured document 1 Algorithm pre. Order(v) visit(v) for each child w of v preorder (w) Make Money Fast! 2 5 1. Motivations 9 2. Methods 3 4 1. 1 Greed 1. 2 Avidity 6 2. 1 Stock Fraud 7 2. 2 Ponzi Scheme References 8 2. 3 Bank Robbery

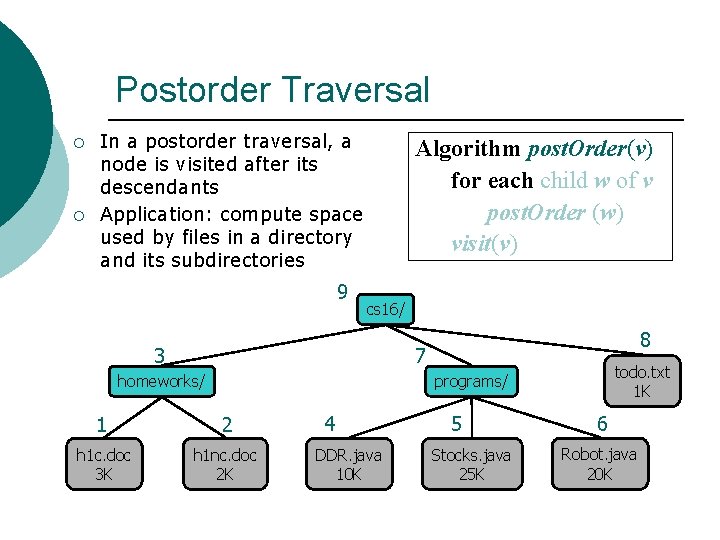
Postorder Traversal ¡ ¡ In a postorder traversal, a node is visited after its descendants Application: compute space used by files in a directory and its subdirectories 9 Algorithm post. Order(v) for each child w of v post. Order (w) visit(v) cs 16/ 3 8 7 homeworks/ todo. txt 1 K programs/ 1 2 h 1 c. doc 3 K h 1 nc. doc 2 K 4 DDR. java 10 K 5 Stocks. java 25 K 6 Robot. java 20 K

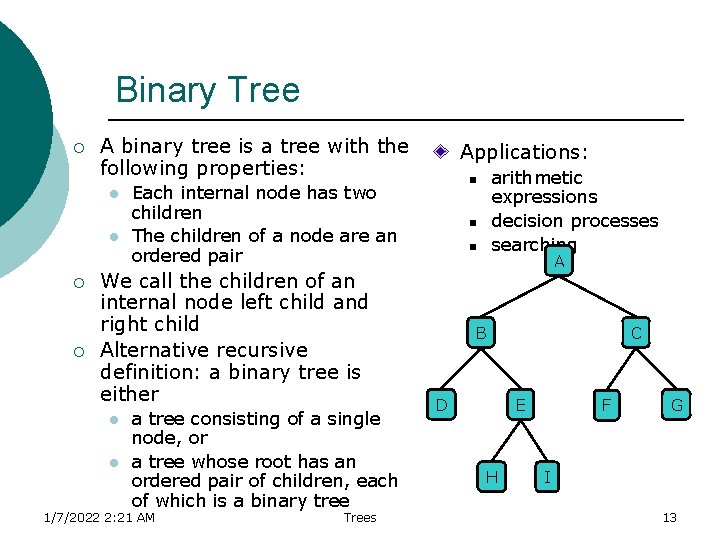
Binary Tree ¡ A binary tree is a tree with the following properties: l l ¡ ¡ l a tree consisting of a single node, or a tree whose root has an ordered pair of children, each of which is a binary tree 1/7/2022 2: 21 AM Trees arithmetic expressions decision processes searching n Each internal node has two children The children of a node are an ordered pair We call the children of an internal node left child and right child Alternative recursive definition: a binary tree is either l Applications: n n A B D C E H F G I 13

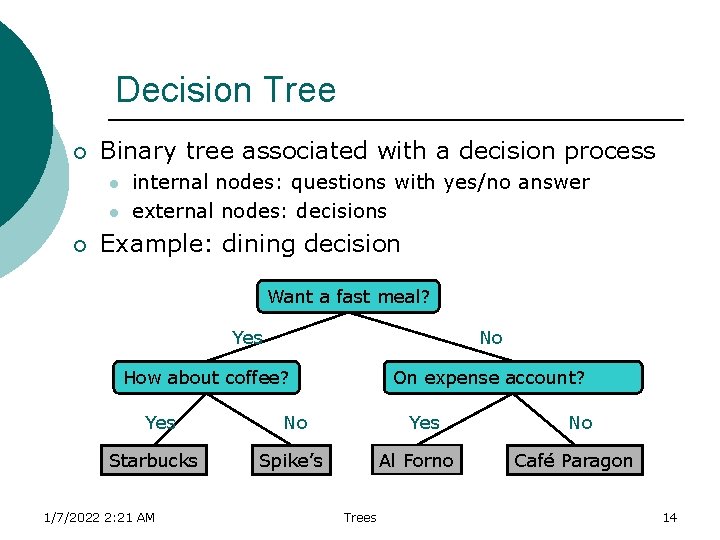
Decision Tree ¡ Binary tree associated with a decision process l l ¡ internal nodes: questions with yes/no answer external nodes: decisions Example: dining decision Want a fast meal? No Yes How about coffee? Yes Starbucks 1/7/2022 2: 21 AM On expense account? No Yes Spike’s Al Forno Trees No Café Paragon 14

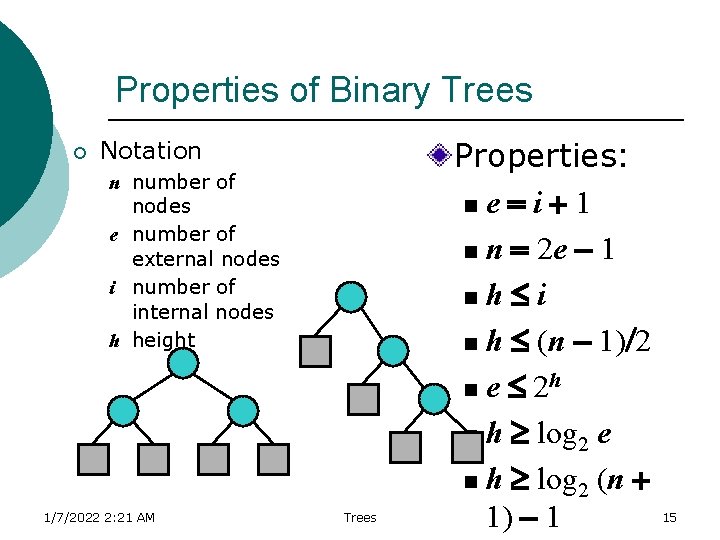
Properties of Binary Trees ¡ Notation n number of nodes e number of external nodes i number of internal nodes h height 1/7/2022 2: 21 AM Trees Properties: ne = i + 1 n n = 2 e - 1 nh i n h (n - 1)/2 n e 2 h n h log 2 e n h log 2 (n + 1) - 1 15

Binary. Tree ADT ¡ The Binary. Tree ADT extends the Tree ADT, i. e. , it inherits all the methods of the Tree ADT ¡ Additional methods: l position left. Child(p) l position right. Child(p) l position sibling(p) 1/7/2022 2: 21 AM Trees ¡ Update methods may be defined by data structures implementing the Binary. Tree ADT 16

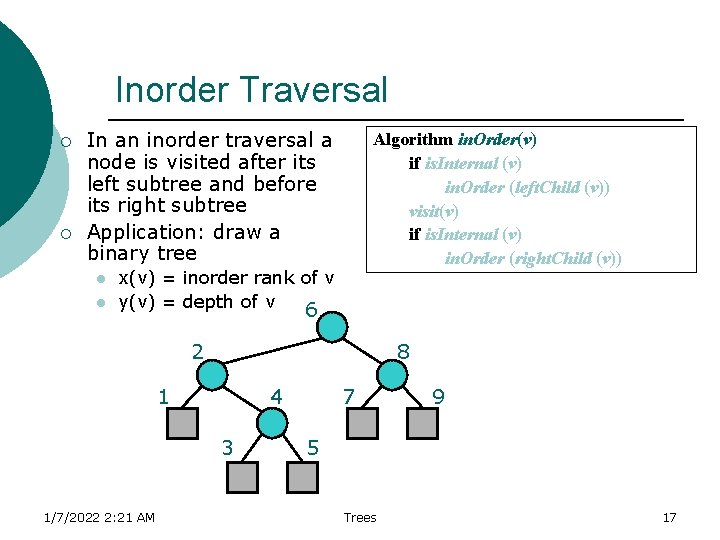
Inorder Traversal ¡ ¡ In an inorder traversal a node is visited after its left subtree and before its right subtree Application: draw a binary tree l l Algorithm in. Order(v) if is. Internal (v) in. Order (left. Child (v)) visit(v) if is. Internal (v) in. Order (right. Child (v)) x(v) = inorder rank of v y(v) = depth of v 6 2 8 1 4 3 1/7/2022 2: 21 AM 7 9 5 Trees 17

Expression Notation ¡ There are three common notations for expressions: l l l Prefix: operator come before operands. Postfix: operator come after operands. Infix: Binary operator come between operands. ¡ Unary operator come before the operand. ¡

Examples ¡ Infix: (a+b)*(c-d/f/(g+h)) l ¡ Prefix: *+ab-c//df+gh l l ¡ Used by human being. E. g. functional language such as Lisp: (* (+ a b) (- c (/ d (/ f (+ g h))))) Postfix: ab+cdf/gh+/-* l E. g. Postfix calculator

Expression Trees ¡ An expression tree can be used to represent an expression. l l l Operator: root Operands: child sub-trees Variable and constants: leaf nodes.

Traversals of Expression Trees Preorder traversal => prefix notation. ¡ Postorder traversal => postfix notation. ¡ Inorder traversal with parenthesis added => infix notation. ¡

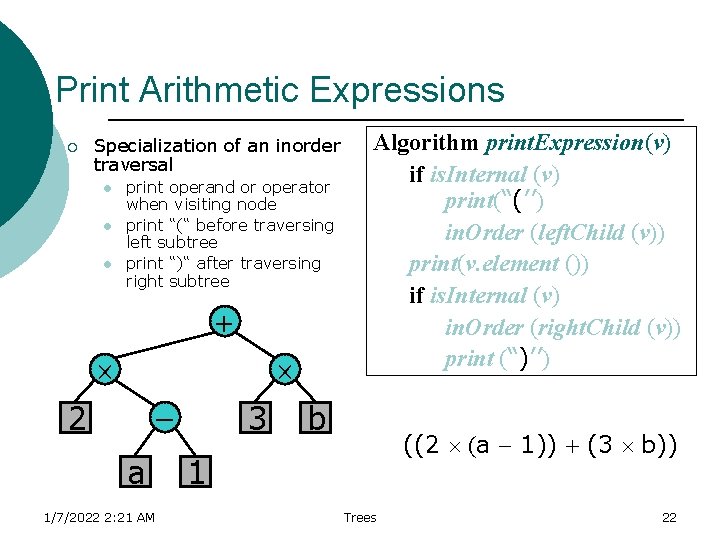
Print Arithmetic Expressions ¡ Specialization of an inorder traversal l print operand or operator when visiting node print “(“ before traversing left subtree print “)“ after traversing right subtree + - 2 a 1/7/2022 2: 21 AM 3 Algorithm print. Expression(v) if is. Internal (v) print(“(’’) in. Order (left. Child (v)) print(v. element ()) if is. Internal (v) in. Order (right. Child (v)) print (“)’’) b ((2 (a - 1)) + (3 b)) 1 Trees 22

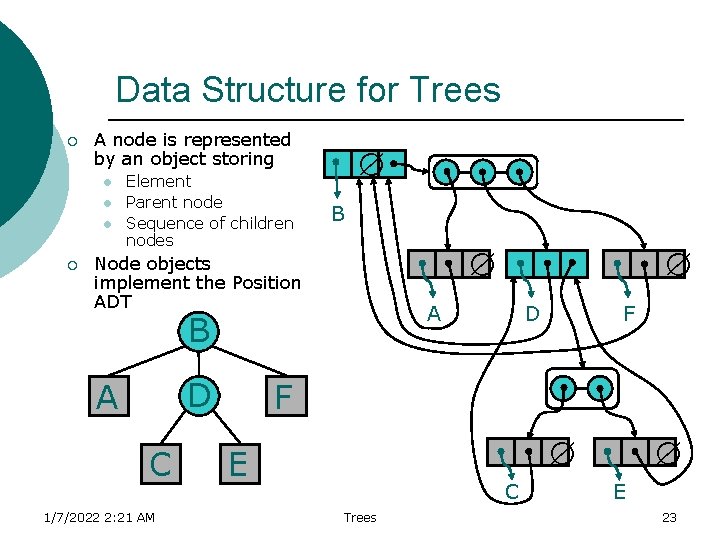
Data Structure for Trees ¡ A node is represented by an object storing l l l ¡ Element Parent node Sequence of children nodes B Node objects implement the Position ADT A B D A C 1/7/2022 2: 21 AM D F F E C Trees E 23

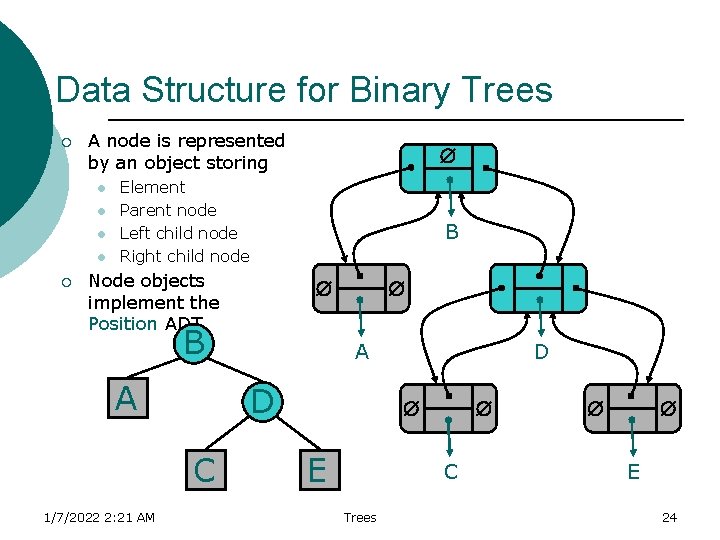
Data Structure for Binary Trees ¡ A node is represented by an object storing l l ¡ Element Parent node Left child node Right child node B Node objects implement the Position ADT B A A D C 1/7/2022 2: 21 AM D E C Trees E 24

Questions and Comments?