CSCI 3333 Data Structures Sorting by Dr Bun

CSCI 3333 Data Structures Sorting by Dr. Bun Yue Professor of Computer Science yue@uhcl. edu http: //sce. uhcl. edu/yue/ 2013

Acknowledgement Mr. Charles Moen ¡ Dr. Wei Ding ¡ Ms. Krishani Abeysekera ¡ Dr. Michael Goodrich ¡

Sorting Arrange objects in ascending or descending key order. ¡ Why sorting? ¡ l l l Used by other algorithms, such as searching (e. g. binary search). Reporting. Data Analysis

Sorting Consideration Each object has a key (which may or may not be unique). ¡ The key forms a total order. ¡ Object order is arranged by key comparison. ¡

Sorting Variation ¡ Internal or external: l Internal: objects stored in primary memory. ¡ l Performance: measure CPU and memory operations. External: objects (records) mainly stored in secondary memory. ¡ Performance: measure: l l CPU and memory operations File I/O operation.

Sorting Variations ¡ Data structures to be sorted: l l Random accessible: e. g. array. Sequentially accessible: e. g. traditional linked list.

Sorting Performance ¡ To measure: l Primitive operations Number of key comparisons ¡ Number of object movement ¡ l ¡ Memory usage Scenarios: l l Average case Worst case

Sorting Algorithms ¡ Many sorting algorithm exists: l l l l Insertion sort Selection sort Bubble sort Quick sort Merge sort Radix sort Heap sort …

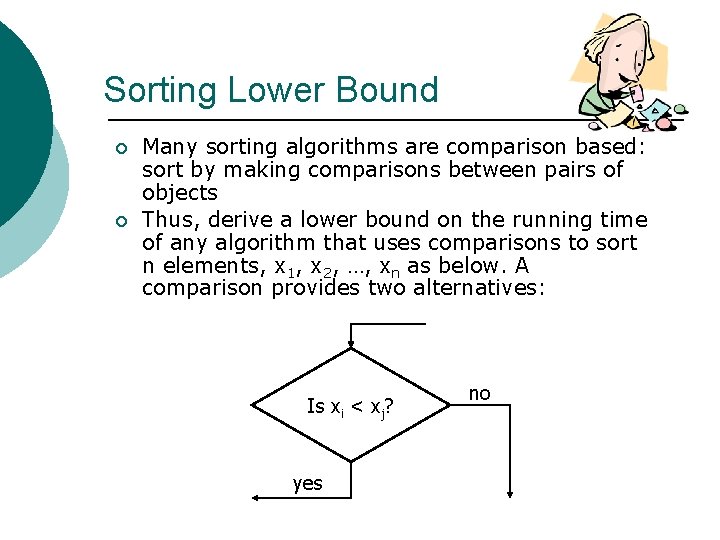
Sorting Lower Bound ¡ ¡ Many sorting algorithms are comparison based: sort by making comparisons between pairs of objects Thus, derive a lower bound on the running time of any algorithm that uses comparisons to sort n elements, x 1, x 2, …, xn as below. A comparison provides two alternatives: Is xi < xj? yes no

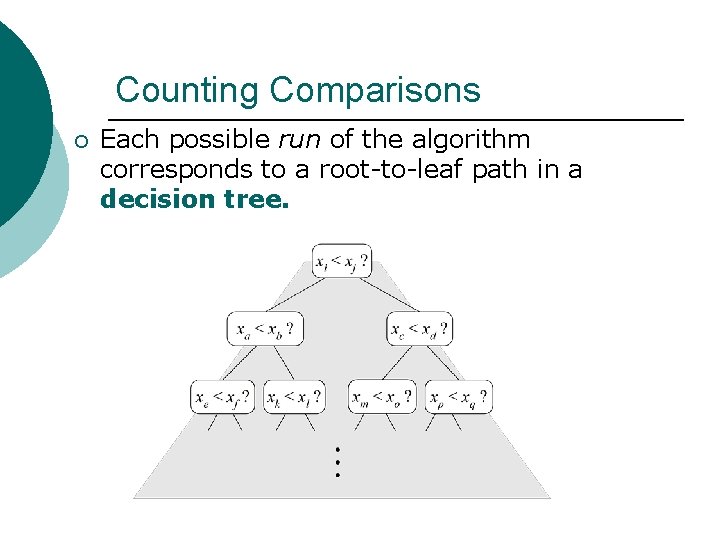
Counting Comparisons ¡ Each possible run of the algorithm corresponds to a root-to-leaf path in a decision tree.

Decision Tree Height ¡ ¡ The shortest possible height of this decision tree is a lower bound on the running time. Every possible input permutation must lead to a separate leaf output. l If not, some input … 4… 5… would have the same output ordering as … 5… 4…, which would be wrong.

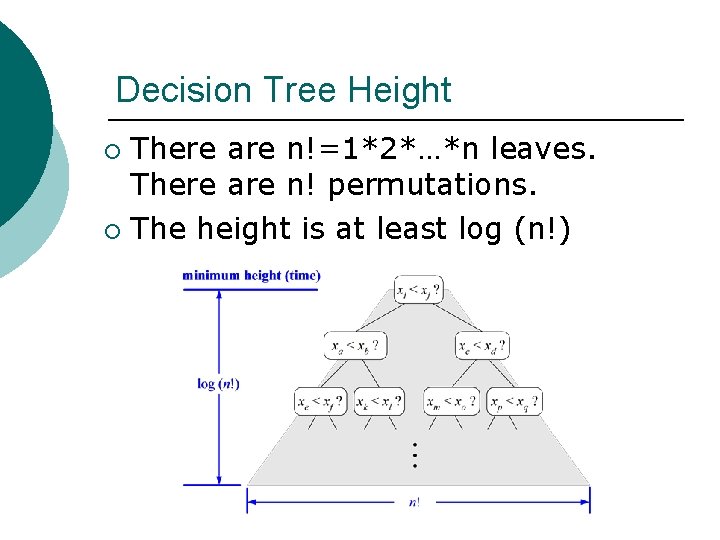
Decision Tree Height There are n!=1*2*…*n leaves. There are n! permutations. ¡ The height is at least log (n!) ¡

The Lower Bound ¡ ¡ ¡ Any comparison-based sorting algorithms takes at least log (n!) time Therefore, any such algorithm takes time at least That is, any comparison-based sorting algorithm must run in Ω(n log n) time.

Sorting Lower Bound Note that we have not analyzed any sorting algorithm. ¡ We have analyze the sorting problem, not a specific solution. ¡ Thus, it is not possible to find a (binary) comparison based algorithm with better than O(n lg n) time complexity! ¡

Questions and Comments?