CSCI 3333 Data Structures Queues Acknowledgement Dr Bun

CSCI 3333 Data Structures Queues

Acknowledgement Dr. Bun Yue ¡ Mr. Charles Moen ¡ Dr. Wei Ding ¡ Ms. Krishani Abeysekera ¡ Dr. Michael Goodrich ¡ Dr. Richard F. Gilberg ¡

Queues ¡ First In First Out (FIFO) data structure.

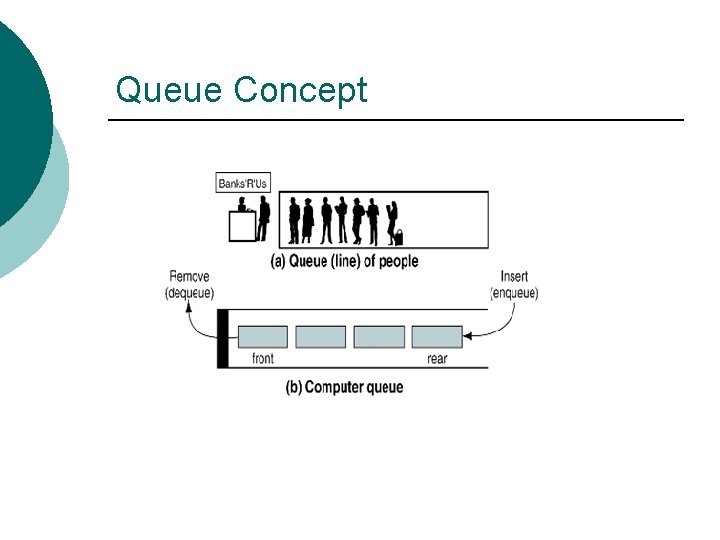
Queue Concept

Queues ¡ ¡ The Queue ADT stores arbitrary objects Insertions and deletions follow the first-in first-out scheme Insertions are at the rear of the queue and removals are at the front of the queue Main queue operations: l l enqueue(object): inserts an element at the end of the queue object dequeue(): removes and returns the element at the front of the queue

Queue Operations ¡ Some auxiliary queue operations: l l l ¡ object front(): returns the element at the front without removing it integer size(): returns the number of elements stored boolean is. Empty(): indicates whether no elements are stored Exceptions l Attempting the execution of dequeue or front on an empty queue throws an Empty. Queue. Exception

Queue Example Operation enqueue(5) enqueue(3) dequeue() enqueue(7) dequeue() front() dequeue() is. Empty() enqueue(9) enqueue(7) size() enqueue(3) enqueue(5) dequeue() Output Q – (5) – (5, 3) 5 (3) – (3, 7) 3 (7) 7 () “error” () true () – (9, 7) 2 (9, 7) – (9, 7, 3, 5) 9 (7, 3, 5)

Some Implementation Criteria ¡ As queues are general data structures for widespread use, there are variations to fit different applications. Some considerations: l l l Implementation: array vs. linked list. Thread safe or not. Blocking or not. Synchronous or not. Allow null elements or not.

Applications of Queues ¡ Some direct applications l l l ¡ Waiting lists, bureaucracy Access to shared resources (e. g. , printer) Simulation Breadth-first traversals Multiprogramming Messaging Indirect applications l l Auxiliary data structure for algorithms Component of other data structures

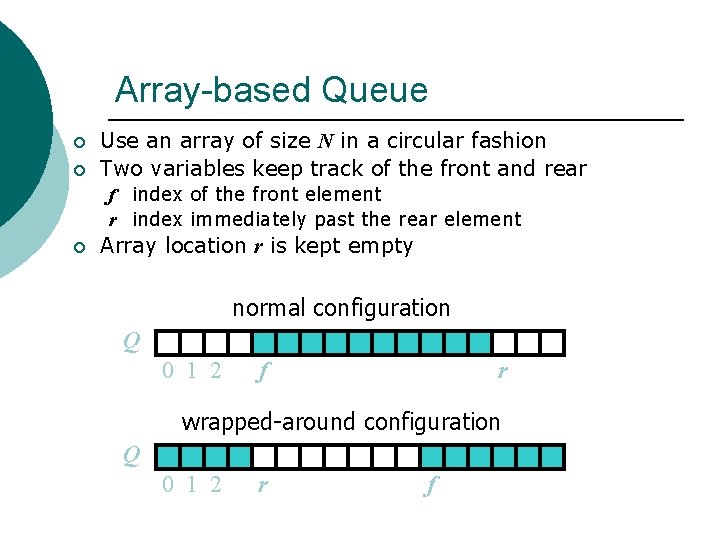
Array-based Queue ¡ ¡ Use an array of size N in a circular fashion Two variables keep track of the front and rear f index of the front element r index immediately past the rear element ¡ Array location r is kept empty normal configuration Q 0 1 2 f r wrapped-around configuration Q 0 1 2 r f

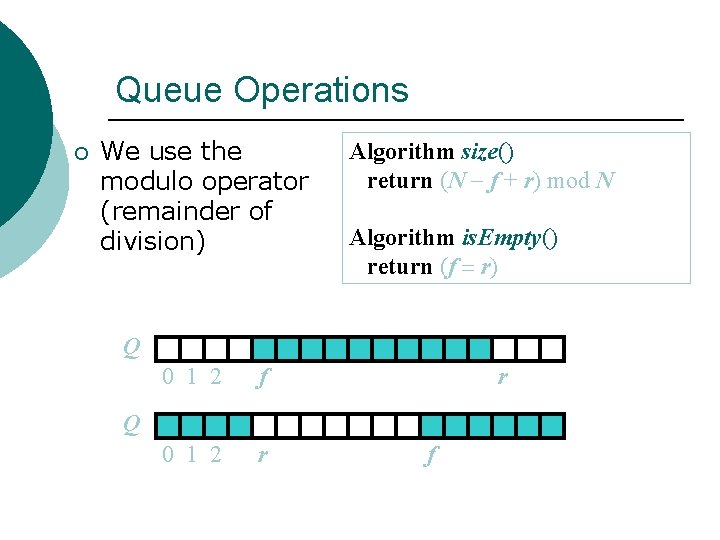
Queue Operations ¡ We use the modulo operator (remainder of division) Algorithm size() return (N f + r) mod N Algorithm is. Empty() return (f = r) Q 0 1 2 f 0 1 2 r r Q f

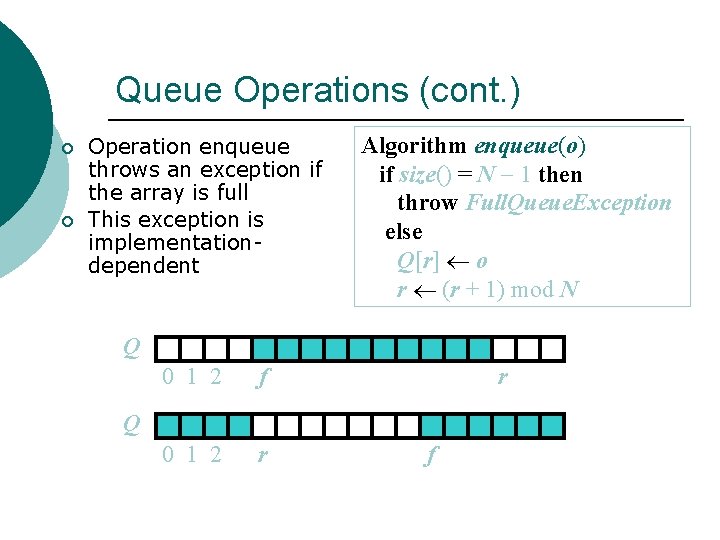
Queue Operations (cont. ) ¡ ¡ Operation enqueue throws an exception if the array is full This exception is implementationdependent Algorithm enqueue(o) if size() = N 1 then throw Full. Queue. Exception else Q[r] o r (r + 1) mod N Q 0 1 2 f 0 1 2 r r Q f

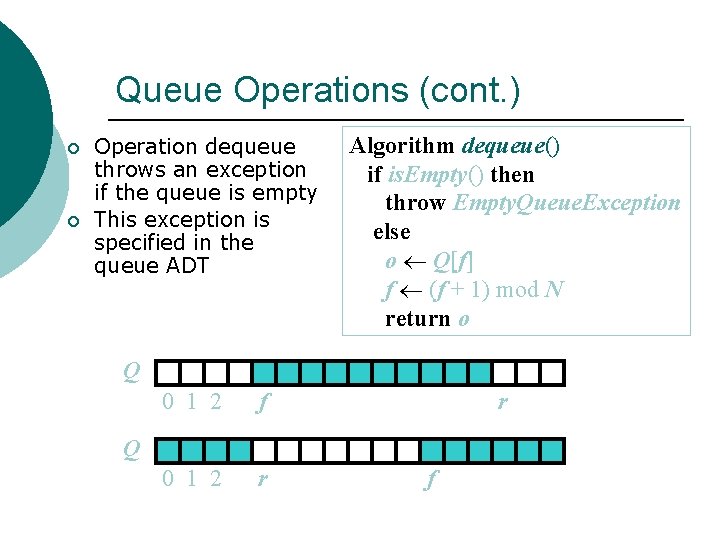
Queue Operations (cont. ) ¡ ¡ Operation dequeue throws an exception if the queue is empty This exception is specified in the queue ADT Algorithm dequeue() if is. Empty() then throw Empty. Queue. Exception else o Q[f] f (f + 1) mod N return o Q 0 1 2 f 0 1 2 r r Q f

Linked List Implementation ¡ We have already implemented methods necessary for the queue ADT (under different method names) using a singly linked list.

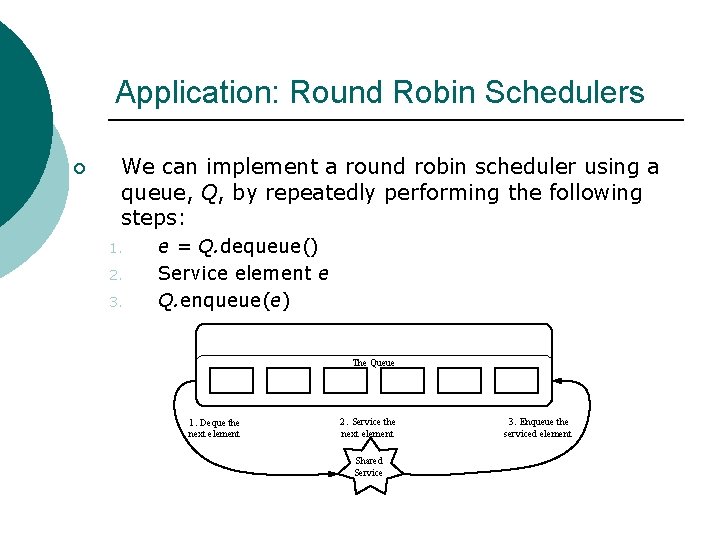
Application: Round Robin Schedulers ¡ We can implement a round robin scheduler using a queue, Q, by repeatedly performing the following steps: 1. 2. 3. e = Q. dequeue() Service element e Q. enqueue(e) The Queue 1. Deque the next element 2. Service the next element Shared Service 3. Enqueue the serviced element

Palindrome in C++: Spot the error #include “Stack. h”; #include “Queue. h”; #include <iostream. h> using namespace std; int main() { // Incorrect solution. Can you see it? Stack S; Queue Q; char ch; cout << “Enter string to be tested as palindrome: “; while (cin >> ch) { S. push(ch); Q. enqueue(ch); } bool pal = true; while (!Q. is. Empty()) pal = Q. dequeue() = = S. pop(); if (pal) cout << “Palindrome!!” << endl; return EXIT_SUCCESS; }

Example: Queue in Ruby is a newer object oriented scripting language using some software engineering principles. ¡ We use a queue example in Ruby to illustrative the use of queues for concurrent processes. ¡ There is no need to understand all details of the example. ¡

Queue. rb require 'thread' queue = Queue. new producer = Thread. new do # concurrent thread 1 5. times do |i| sleep rand(i) # simulate expense queue << i puts "#{i} produced" end consumer = Thread. new do # concurrent thread 2 5. times do |i| value = queue. pop sleep rand(i/2) # simulate expense puts "consumed #{value}" end consumer. join

Executing Queue. rb 0 produced 1 produced consumed 0 2 produced consumed 1 consumed 2 3 produced consumed 3 4 produced consumed 4

Questions and Comments?