CSCI 3333 Data Structures Introduction to Recursion Acknowledgement

CSCI 3333 Data Structures Introduction to Recursion

Acknowledgement Dr. Bun Yue ¡ Mr. Charles Moen ¡ Dr. Wei Ding ¡ Ms. Krishani Abeysekera ¡ Dr. Michael Goodrich ¡ Dr. Behrouz A. Forouzan ¡ Dr. Richard F. Gilberg ¡

Recursion is defining a function that calls itself as a subroutine. ¡ Recursion is a way to combat complexity and solve problems. ¡ Solving a problem by: ¡ l l Solving the problem for ‘trivial’ cases, and Solving the same problem, but with smaller sizes.

Recursive Definition A recursive definition: a definition in terms of itself. Example: ¡ 0 is a natural number. ¡ If x is a natural number, then x+1 is a natural number. (or x is a natural number if x-1 is a natural number). ¡

Recursive Methods A recursive method may calls itself. Example: factorial. Iterative definition: n! = n. (n-1). (n-2) … 3. 2. 1 ¡ Recursive definition:

Recursive Factorial Algorithm //By Forouzan

Factorial Implementation: Fac-1 ¡ Found here in C++: int factorial(int number) { int temp; if (number <= 1) return 1; temp = number * factorial(number - 1); return temp; } ¡ What do you think?

Another Implementation: Fac-2 int recursive. Factorial(int n) { if (n == 0) return 1; // base case else return n * recursive. Factorial(n- 1); // recursive case /general case }

Content of a Recursive Method ¡ ¡ Base case(s): exit conditions l Values of the input variables (exit conditions) for which we perform no recursive calls are called base cases (there should be at least one base case). l Every possible chain of recursive calls must eventually reach a base case. Recursive calls: recursive conditions l Calls to the current method. l Each call must reduce the size of the problem and move it toward the base case; reduces the size of the problem. .

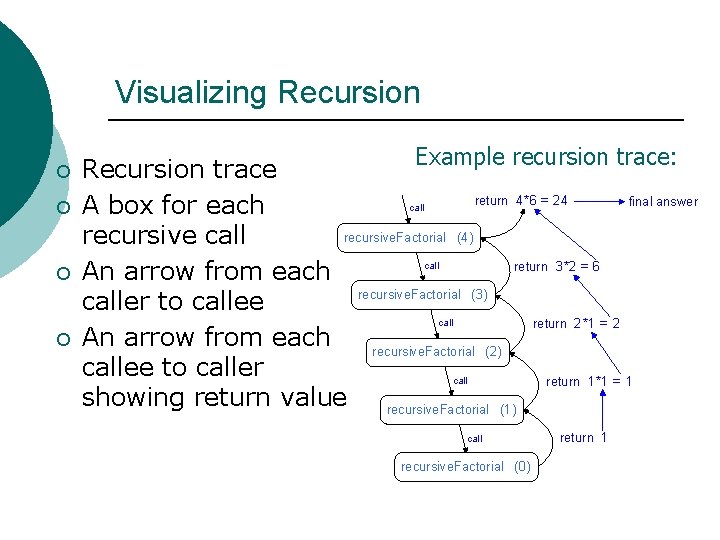
Visualizing Recursion ¡ ¡ ¡ Example recursion trace: Recursion trace return 4*6 = 24 final answer A box for each recursive. Factorial (4) recursive call return 3*2 = 6 An arrow from each recursive. Factorial (3) caller to callee return 2*1 = 2 An arrow from each recursive. Factorial (2) callee to caller return 1*1 = 1 showing return value recursive. Factorial (1) call ¡ call recursive. Factorial (0) return 1

Tips on Recursive Analysis Identify exit and recursive conditions. ¡ Ensure that the conditions cover all input ranges. ¡

Input Range Analysis of Fac ¡ ¡ Fac-1 and Fac-2: n (or number) has the type of int. Fac-2 may be caught in circularity forever for negative numbers.

Reversing an Array Algorithm Reverse. Array(A, i, j): Input: An array A and nonnegative integer indices i and j Output: The reversal of the elements in A starting at index i and ending at j if i < j then Swap A[i] and A[ j] Reverse. Array(A, i + 1, j - 1) return

Tips on Constructing Recursion In creating recursive methods, it is important to define the methods in ways that facilitate recursion. ¡ This sometimes requires we may define additional parameters that are passed to the method. ¡ For example, we defined the array reversal method as Reverse. Array(A, i, j), not Reverse. Array(A). ¡

Computing Powers ¡ The power function, p(x, n)=xn, can be defined recursively: ¡ This leads to an power function that runs in linear time (for we make n recursive calls). We can do better than this, however. ¡

Recursive Squaring ¡ We can derive a more efficient linearly recursive algorithm by using repeated squaring: ¡ For example, 24 = 2(4/2)2 = (22)2 = 42 = 16 25 = 21+(4/2)2 = 2(22)2 = 2(42) = 32 26 = 2(6/ 2)2 = (26/2)2 = (23)2 = 82 = 64 27 = 21+(6/2)2 = 2(23)2 = 2(82) = 128. Note: This definition leads to linear recursive algorithm that uses O(n)

A Recursive Squaring Method Algorithm Power(x, n): Input: A number x and integer n Output: The value xn if n = 0 then return 1 if n is odd then y = Power(x, (n - 1)/ 2) return x · y else y = Power(x, n/ 2) return y · y

Analyzing the Recursive Squaring Method Algorithm Power(x, n): Input: A number x and integer Output: The value xn if n = 0 then return 1 if n is odd then y = Power(x, (n - 1)/ 2) return x · y else y = Power(x, n/ 2) return y · y n Each time we make a recursive call we halve the value of n; hence, we make log n recursive calls. That is, this method runs in O(log n) time. It is important that we used a variable twice here rather than calling the method twice.

Further Analysis Need to limit the range of n, or. ¡ Add the recursive condition: ¡ if n < 0 return 1 / Power(x, -n);

Tail Recursion 1 Tail recursion occurs when a linearly recursive method makes its recursive call as its last step. ¡ The array reversal method is an example. ¡ Such methods can be easily converted to non-recursive methods (which saves on some resources), often by the compiler and runtime system. ¡

Tail Recursion Example Algorithm Iterative. Reverse. Array(A, i, j ): Input: An array A and nonnegative integer indices i and j Output: The reversal of the elements in A starting at index i and ending at j while i < j do Swap A[i ] and A[ j ] i =i+1 j =j-1 return

Tail Recursion 2 Tips: for linear recursion, write your method using tail recursion. ¡ Example: Fac-1 does not use tail recursion. Fac-2 does. ¡

Binary Recursion ¡ ¡ ¡ Binary recursion occurs whenever there are two recursive calls for each non-base case. Also known as Higher-Order Recursion. Example: Fibonacci number l 0, 1, 1, 2, 3, 5, 8, 13, 21, 34

Fibonacci Numbers ¡ Fibonacci numbers are defined recursively: F 0 = 0 F 1 = 1 Fi = Fi-1 + Fi-2 for i > 1.

Binary Recursions are expensive. ¡ If possible, convert it to linear recursion. ¡

Recursive Fibonacci Algorithm Binary. Fib(k): Input: Nonnegative integer k Output: The kth Fibonacci number Fk if k = 1 then return k else return Binary. Fib(k - 1) + Binary. Fib(k - 2) ¡ ¡ Binary recursion from the text book. Any problem here?

A C++ Implementation long fib(unsigned long n) { if (n <= 1) { return n; } else { return fib(n-1)+fib(n-2); } }

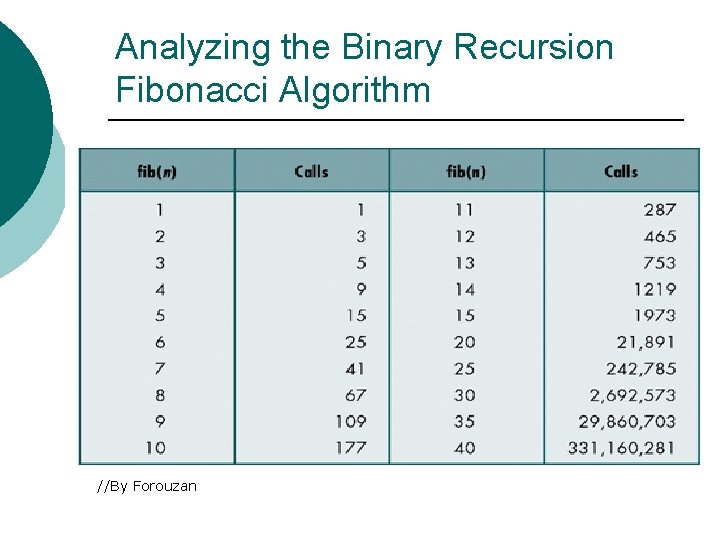
Analyzing the Binary Recursion Fibonacci Algorithm ¡ Let nk denote number of recursive calls made by Binary. Fib(k). Then l l l l l ¡ n 0 n 1 n 2 n 3 n 4 n 5 n 6 n 7 n 8 = = = = = 1 1 n 2 n 3 n 4 n 5 n 6 n 7 + + + + n 0 n 1 n 2 n 3 n 4 n 5 n 6 + + + + 1 1 1 1 = = = = 1+1+1=3 3+1+1=5 5+3+1=9 9 + 5 + 1 = 15 15 + 9 + 1 = 25 25 + 1 = 41 41 + 25 + 1 = 67. Note that the value at least doubles for every other value of nk. That is, nk > 2 k/2. It is exponential!

Analyzing the Binary Recursion Fibonacci Algorithm //By Forouzan

A Better Fibonacci Algorithm ¡ Use linear recursion instead: Algorithm Linear. Fibonacci(k): Input: A nonnegative integer k Output: Pair of Fibonacci numbers (Fk, Fk-1) if k = 1 then return (k, 0) else (i, j) = Linear. Fibonacci(k - 1) return (i +j, i) ¡ Runs in O(k) time.

Questions and Comments?