CSCI 3333 Data Structures Binary Trees by Dr

CSCI 3333 Data Structures Binary Trees by Dr. Bun Yue Professor of Computer Science yue@uhcl. edu http: //sce. uhcl. edu/yue/ 2013

Acknowledgement Mr. Charles Moen ¡ Dr. Wei Ding ¡ Ms. Krishani Abeysekera ¡ Dr. Michael Goodrich ¡

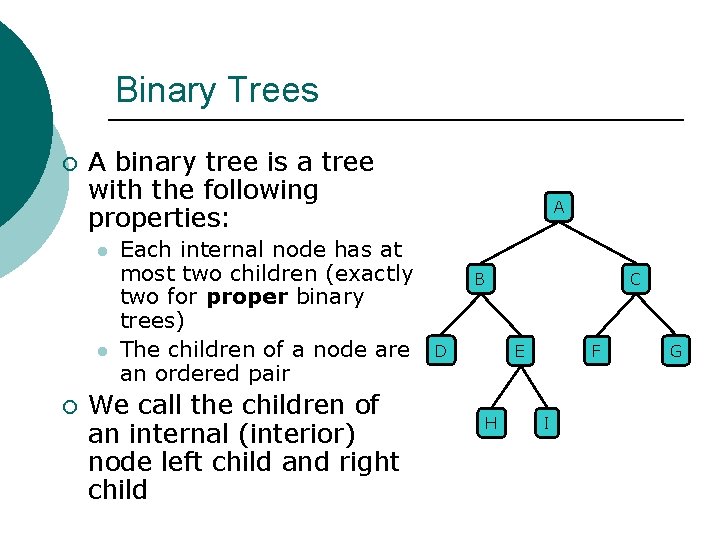
Binary Trees ¡ A binary tree is a tree with the following properties: l l ¡ Each internal node has at most two children (exactly two for proper binary trees) The children of a node are an ordered pair We call the children of an internal (interior) node left child and right child A C B D F E H I G

Binary Tree ¡ Alternative recursive definition: a binary tree is either l l ¡ a tree consisting of a single node, or a tree whose root has an ordered pair of children, each of which is a binary tree. Some Applications: l arithmetic expressions l decision processes l searching

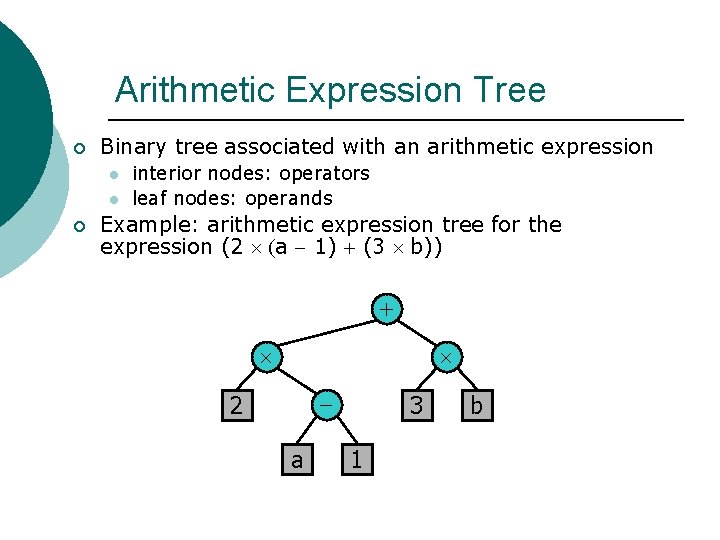
Arithmetic Expression Tree ¡ Binary tree associated with an arithmetic expression l l ¡ interior nodes: operators leaf nodes: operands Example: arithmetic expression tree for the expression (2 (a - 1) + (3 b)) + - 2 a 3 1 b

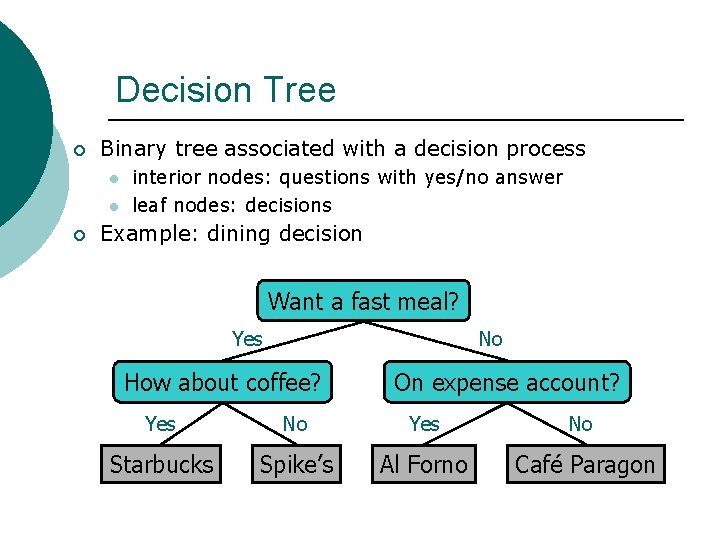
Decision Tree ¡ Binary tree associated with a decision process l l ¡ interior nodes: questions with yes/no answer leaf nodes: decisions Example: dining decision Want a fast meal? No Yes How about coffee? On expense account? Yes No Starbucks Spike’s Al Forno Café Paragon

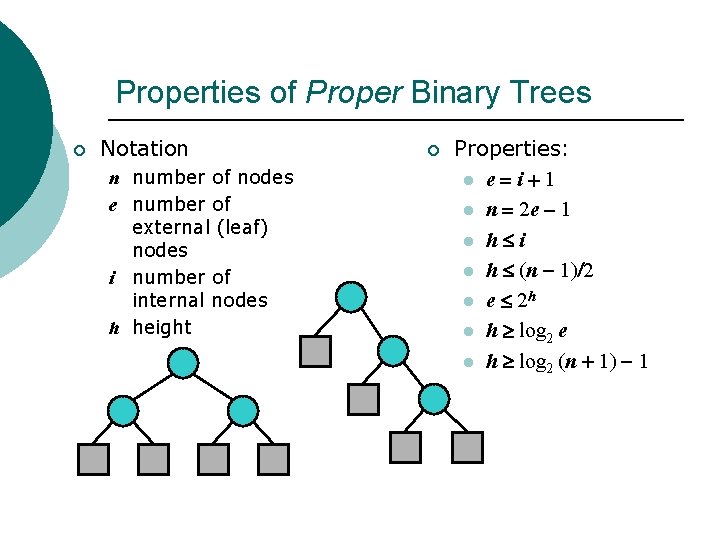
Properties of Proper Binary Trees ¡ Notation n number of nodes e number of external (leaf) nodes i number of internal nodes h height ¡ Properties: l e=i+1 l n = 2 e - 1 l h i l h (n - 1)/2 l e 2 h l h log 2 e l h log 2 (n + 1) - 1

Binary. Tree ADT ¡ ¡ The Binary. Tree ADT extends the Tree ADT, i. e. , it inherits all the methods of the Tree ADT Additional methods: l l position boolean left(p) right(p) has. Left(p) has. Right(p) ¡ Update methods may be defined by data structures implementing the Binary. Tree ADT

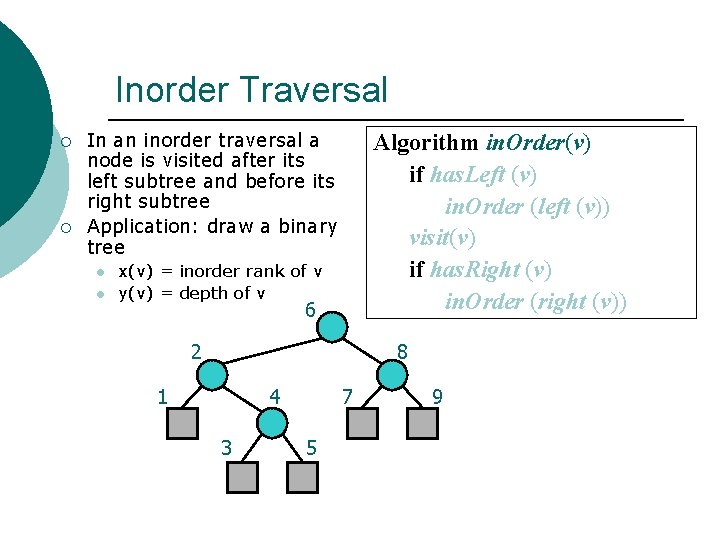
Inorder Traversal ¡ ¡ In an inorder traversal a node is visited after its left subtree and before its right subtree Application: draw a binary tree l l Algorithm in. Order(v) if has. Left (v) in. Order (left (v)) visit(v) if has. Right (v) in. Order (right (v)) x(v) = inorder rank of v y(v) = depth of v 6 2 8 1 4 3 7 5 9

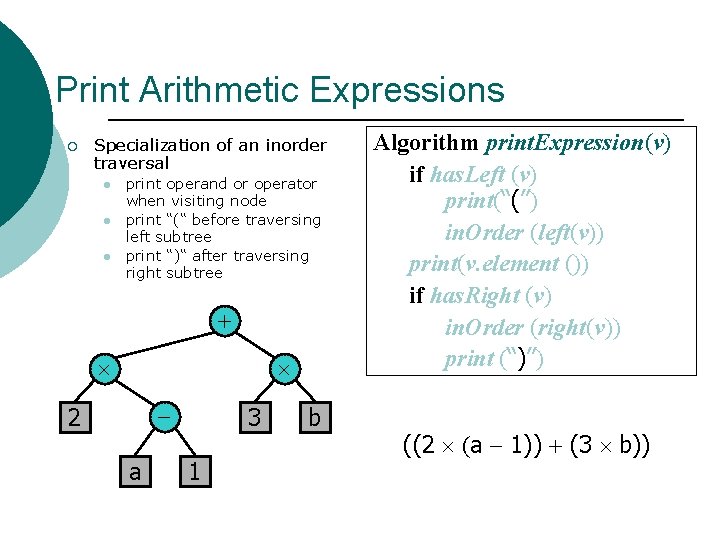
Print Arithmetic Expressions ¡ Specialization of an inorder traversal l print operand or operator when visiting node print “(“ before traversing left subtree print “)“ after traversing right subtree + - 2 a 3 1 b Algorithm print. Expression(v) if has. Left (v) print(“(’’) in. Order (left(v)) print(v. element ()) if has. Right (v) in. Order (right(v)) print (“)’’) ((2 (a - 1)) + (3 b))

Evaluate Arithmetic Expressions ¡ Specialization of a postorder traversal l l recursive method returning the value of a subtree when visiting an internal node, combine the values of the subtrees

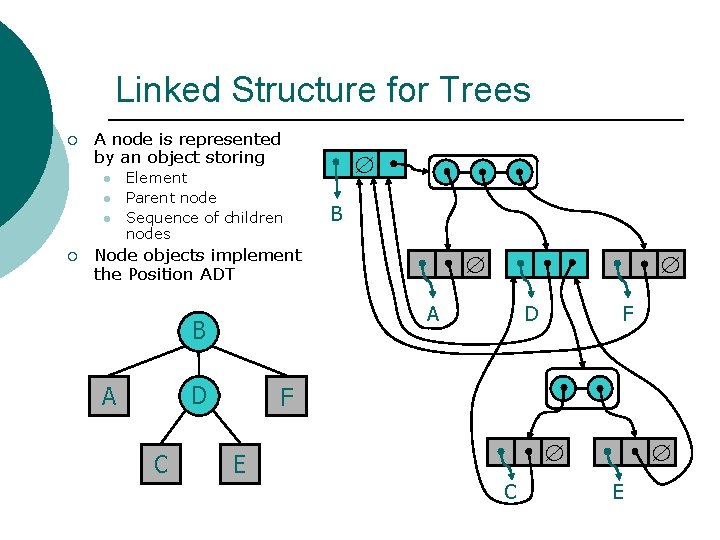
Linked Structure for Trees ¡ A node is represented by an object storing l l l ¡ Element Parent node Sequence of children nodes B Node objects implement the Position ADT D C A B A D F F E C E

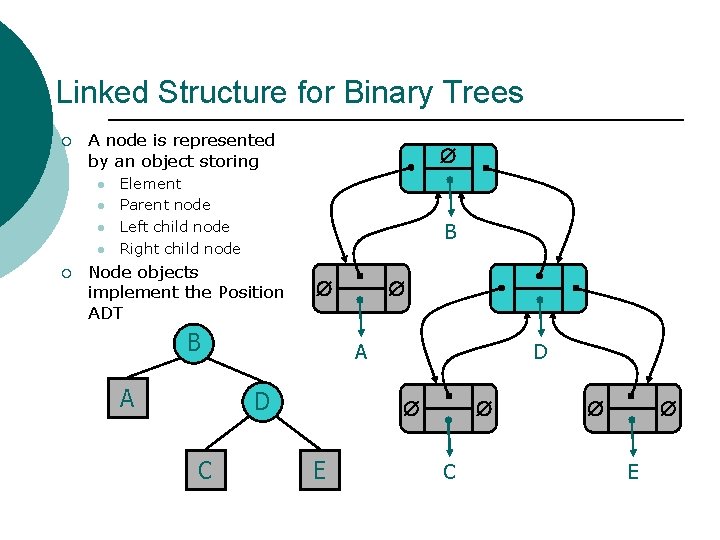
Linked Structure for Binary Trees ¡ A node is represented by an object storing l l ¡ Element Parent node Left child node Right child node B Node objects implement the Position ADT B A A D C D E C E

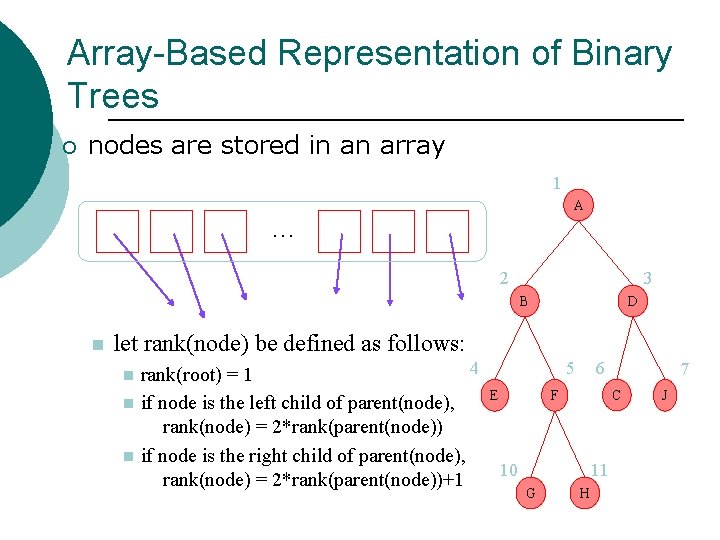
Array-Based Representation of Binary Trees ¡ nodes are stored in an array 1 A … 2 3 B n D let rank(node) be defined as follows: n n n 4 rank(root) = 1 if node is the left child of parent(node), rank(node) = 2*rank(parent(node)) if node is the right child of parent(node), rank(node) = 2*rank(parent(node))+1 5 E 6 C F 10 11 G 7 H J

Space Complexity Big-Oh for Memory Requirement. ¡ Linked Structures worst case: O(n), where n is the number of nodes. ¡ Array Representation Worst case: O(2 n) => not acceptable for many general binary tree applications. ¡

Questions and Comments?