CSCI 2950 C Lecture 8 Molecular Phylogeny Parsimony





































- Slides: 65

CSCI 2950 -C Lecture 8 Molecular Phylogeny: Parsimony and Likelihood http: //cs. brown. edu/courses/csci 2950 -c/

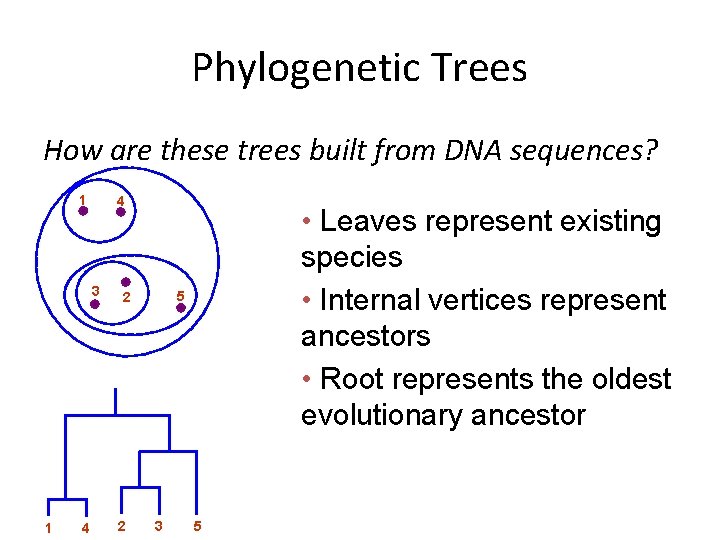
Phylogenetic Trees How are these trees built from DNA sequences? 1 4 3 1 4 5 2 2 • Leaves represent existing species • Internal vertices represent ancestors • Root represents the oldest evolutionary ancestor 3 5

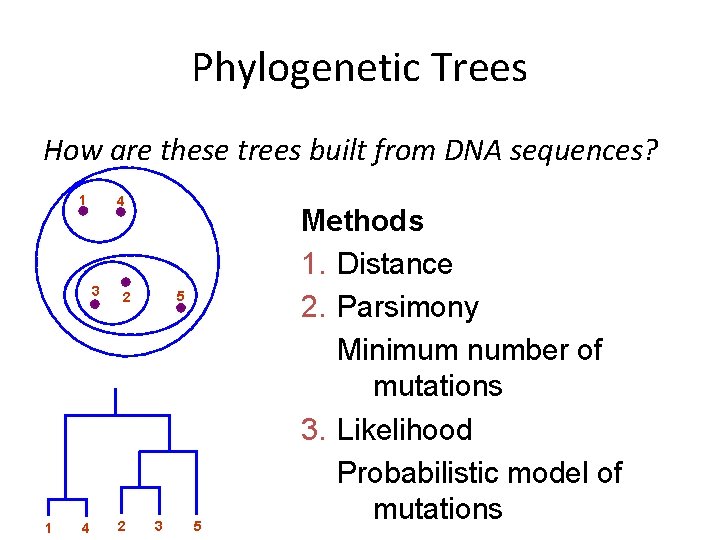
Phylogenetic Trees How are these trees built from DNA sequences? 1 4 3 1 4 5 2 2 3 5 Methods 1. Distance 2. Parsimony Minimum number of mutations 3. Likelihood Probabilistic model of mutations

Outline Last Lecture: distance-based Methods • Additive distances • 4 Point condition • UPGMA & Neighbor joining Today: • Parsimony-based methods • Sankoff + Fitch’s algorithms • Likelihood Methods • Perfect Phylogeny

Weighted Small Parsimony Problem: Formulation • Input: Tree T with each leaf labeled by elements of a k-letter alphabet and a k x k scoring matrix ( ij) • Output: Labeling of internal vertices of the tree T minimizing the weighted parsimony score

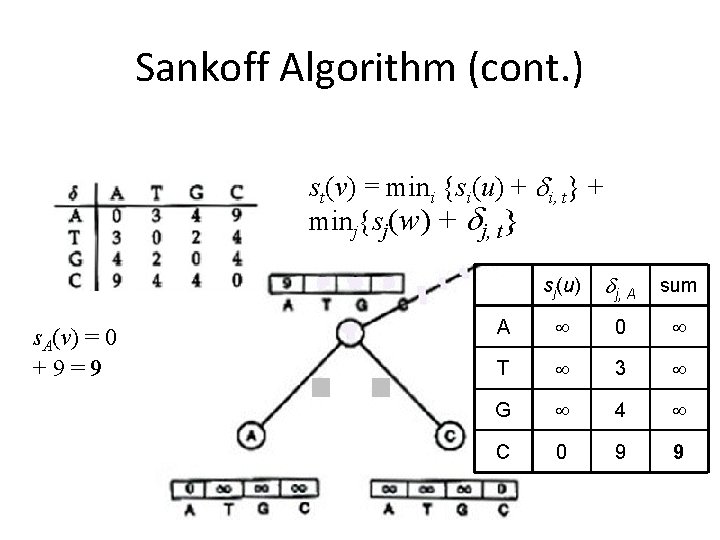
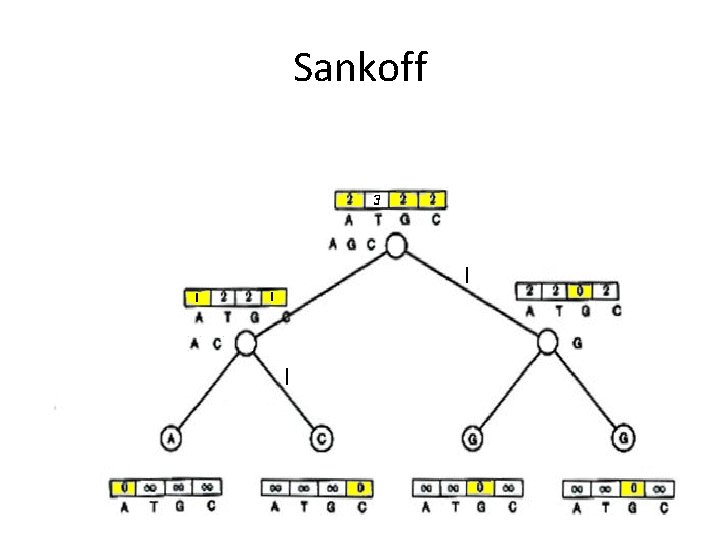
Sankoff Algorithm Dynamic Programming • Calculate and keep track of a score for every possible label at each vertex – st(v) = minimum parsimony score of the subtree rooted at vertex v if v has character t • The score at each vertex is based on scores of its children: – st(parent) = mini {si( left child ) + i, t} + minj {sj( right child ) + j, t}

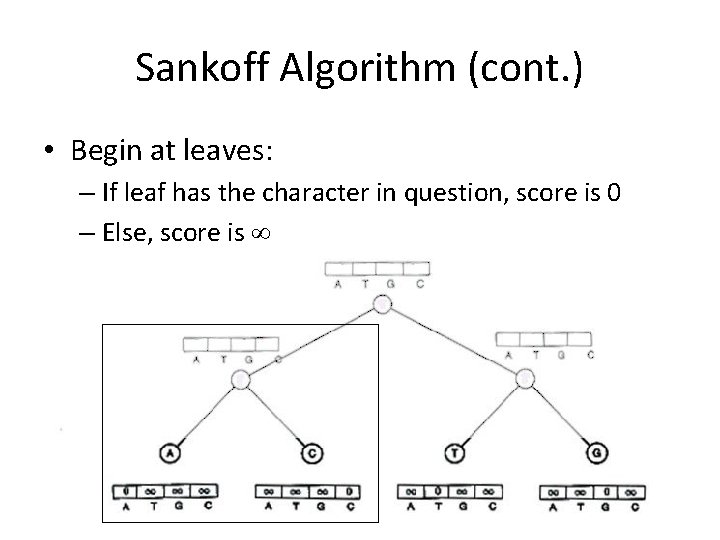
Sankoff Algorithm (cont. ) • Begin at leaves: – If leaf has the character in question, score is 0 – Else, score is

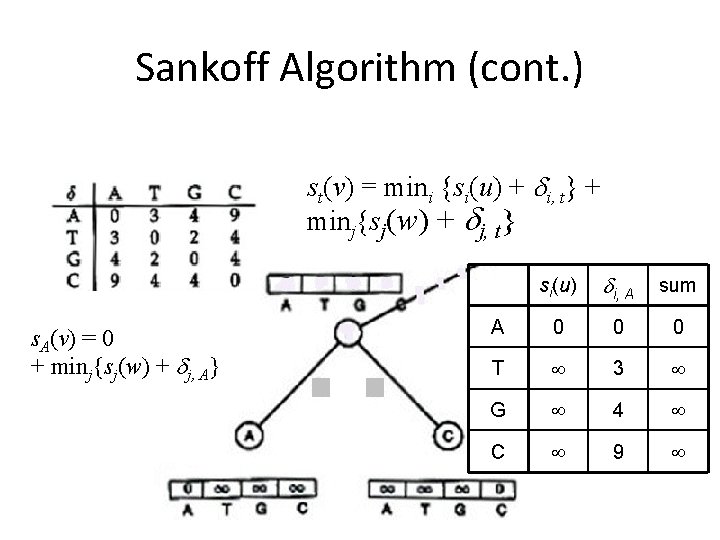
Sankoff Algorithm (cont. ) st(v) = mini {si(u) + i, t} + minj{sj(w) + j, t} s. A(v) = 0 mini{si(u) + i, A} + minj{sj(w) + j, A} si(u) i, A sum A 0 0 0 T 3 G 4 C 9

Sankoff Algorithm (cont. ) st(v) = mini {si(u) + i, t} + minj{sj(w) + j, t} s. A(v) = 0 mini{si(u) + i, A} + 9 min = 9 j{sj(w) + j, A} sj(u) j, A sum A 0 T 3 G 4 C 0 9 9

Sankoff Algorithm (cont. ) st(v) = mini {si(u) + i, t} + minj{sj(w) + j, t} Repeat for T, G, and C

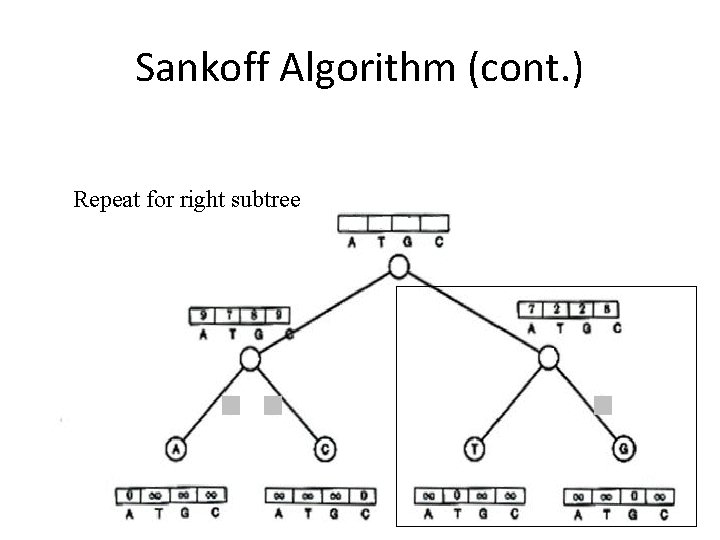
Sankoff Algorithm (cont. ) Repeat for right subtree

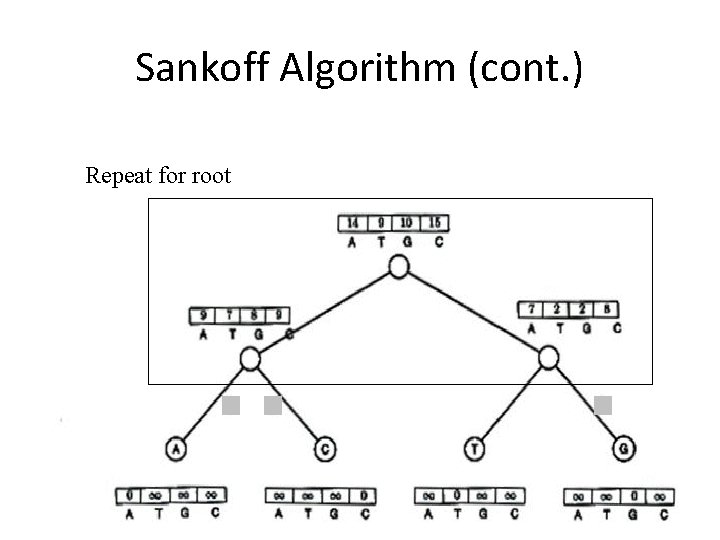
Sankoff Algorithm (cont. ) Repeat for root

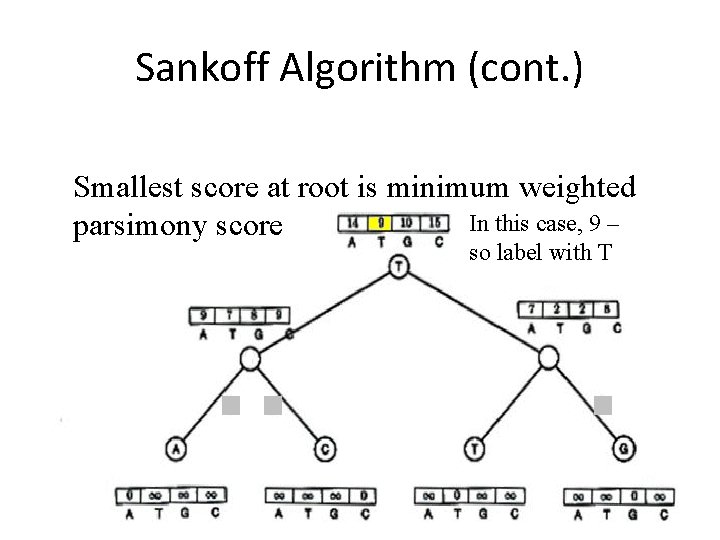
Sankoff Algorithm (cont. ) Smallest score at root is minimum weighted In this case, 9 – parsimony score so label with T

Sankoff Algorithm: Traveling down the Tree • The scores at the root vertex have been computed by going up the tree • After the scores at root vertex are computed the Sankoff algorithm moves down the tree and assign each vertex with optimal character.

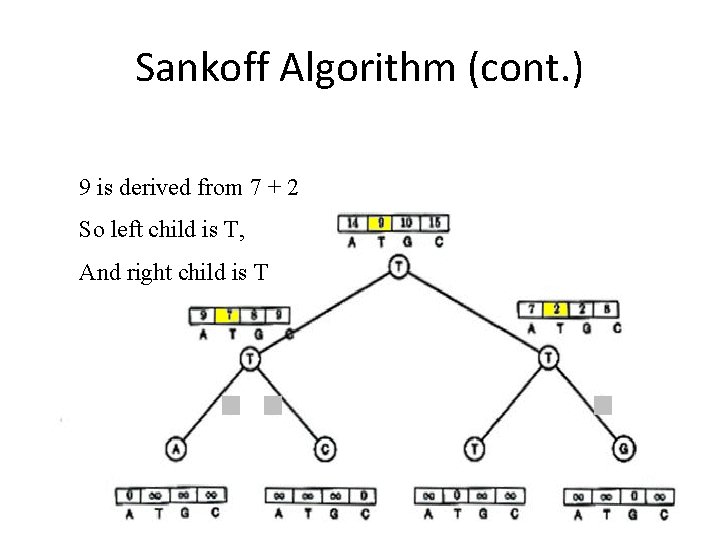
Sankoff Algorithm (cont. ) 9 is derived from 7 + 2 So left child is T, And right child is T

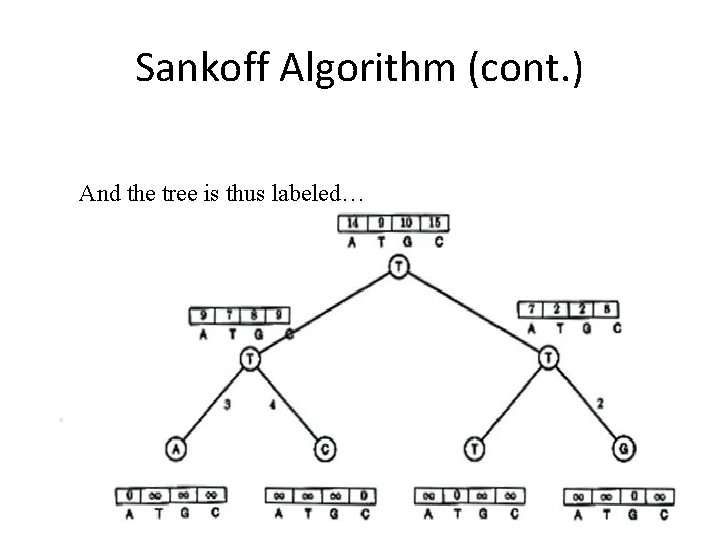
Sankoff Algorithm (cont. ) And the tree is thus labeled…

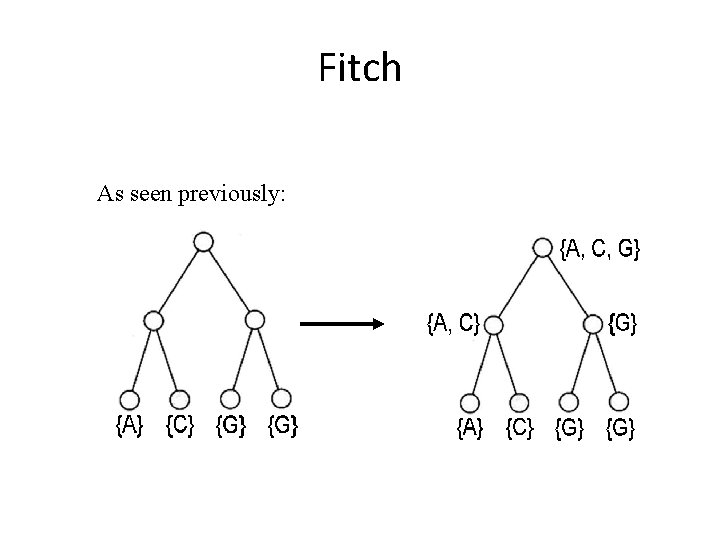
Fitch’s Algorithm • Solves Small Parsimony problem – Published 4 years before Sankoff (1971) • Assigns a set of letters to every vertex in the tree, S(v) • S(l) = observed character for each leaf l

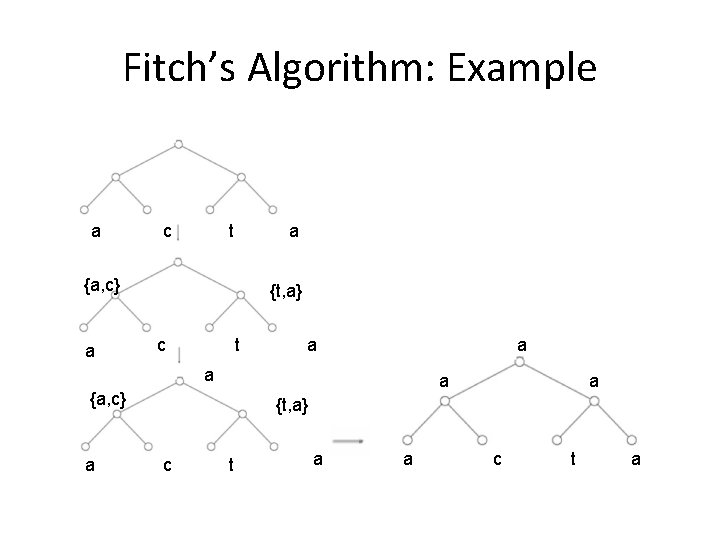
Fitch’s Algorithm: Example a c t a {a, c} a {t, a} c t a a {a, c} a a {t, a} c t a a c t a

Fitch Algorithm 1) Assign a set of possible letters Sv to every vertex v, traversing the tree from leaves to root • For vertex v with children u and w: – Sv = Su “intersect” Sw if non-empty intersection Su “union” Sw , otherwise – E. g. if the node we are looking at has a left child labeled {A, C} and a right child labeled {A, T}, the node will be given the set {A, C, T}

Fitch Algorithm (cont. ) 2) Assign labels to each vertex, traversing the tree from root to leaves • Assign root arbitrarily from its set of letters • For all other vertices, if its parent’s label is in its set of letters, assign it its parent’s label • Else, choose an arbitrary letter from its set as its label

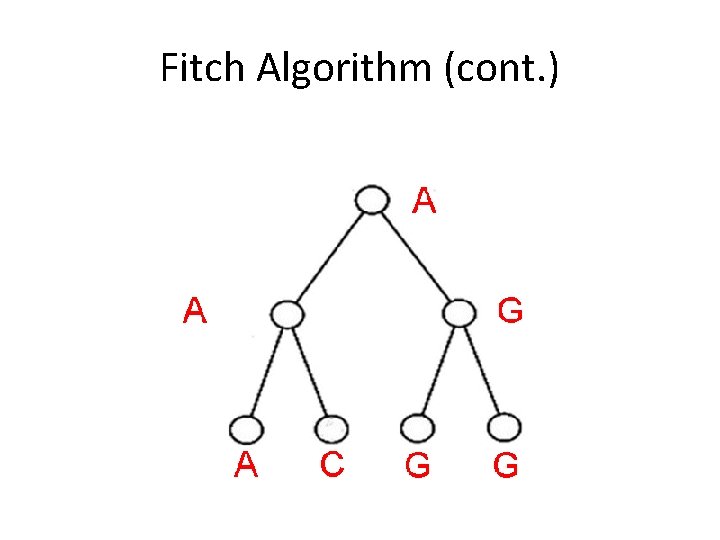
Fitch Algorithm (cont. )

Fitch vs. Sankoff • Both have an O(nk) runtime • Are they actually different? • Let’s compare …

Fitch As seen previously:

Comparison of Fitch and Sankoff • As seen earlier, the scoring matrix for the Fitch algorithm is merely: A T G C A 0 1 1 1 T 1 0 1 1 G 1 1 0 1 C 1 1 1 0 • So let’s do the same problem using Sankoff algorithm and this scoring matrix

Sankoff

Sankoff vs. Fitch • The Sankoff algorithm gives the same set of optimal labels as the Fitch algorithm • For Sankoff algorithm, character t is optimal for vertex v if st(v) = min 1<i<ksi(v) • Let Sv = set of optimal letters for v. • Then – Sv = Su “intersect” Sw if non-empty intersection Su “union” Sw , otherwise • This is also the Fitch recurrence • The two algorithms are identical

Large Parsimony Problem • Input: An n x m matrix M describing n species, each represented by an m-character string • Output: A tree T with n leaves labeled by the n rows of matrix M, and a labeling of the internal vertices such that the parsimony score is minimized over all possible trees and all possible labelings of internal vertices

Large Parsimony Problem (cont. ) • Possible search space is huge, especially as n increases – (2 n – 3)!! possible rooted trees – (2 n – 5)!! possible unrooted trees • Problem is NP-complete – Exhaustive search only possible w/ small n(< 10) • Hence, branch and bound or heuristics used

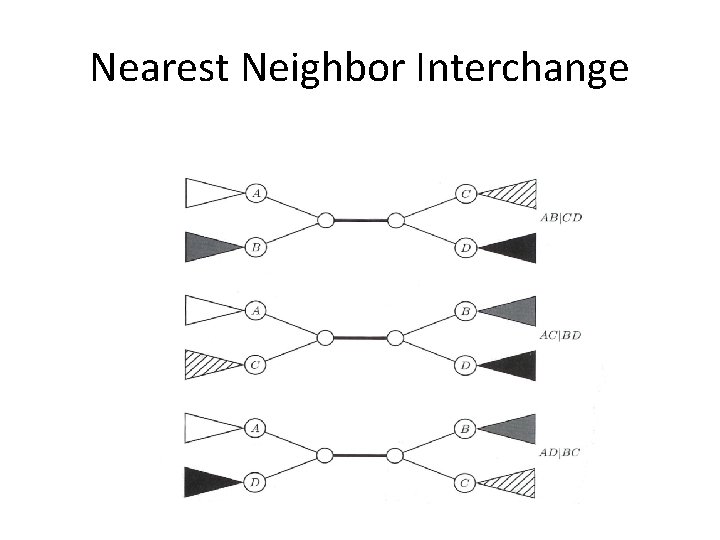
Nearest Neighbor Interchange A Greedy Algorithm • A Branch Swapping algorithm • Only evaluates a subset of all possible trees • Defines a neighbor of a tree as one reachable by a nearest neighbor interchange – A rearrangement of the four subtrees defined by one internal edge – Only three different rearrangements per edge

Nearest Neighbor Interchange

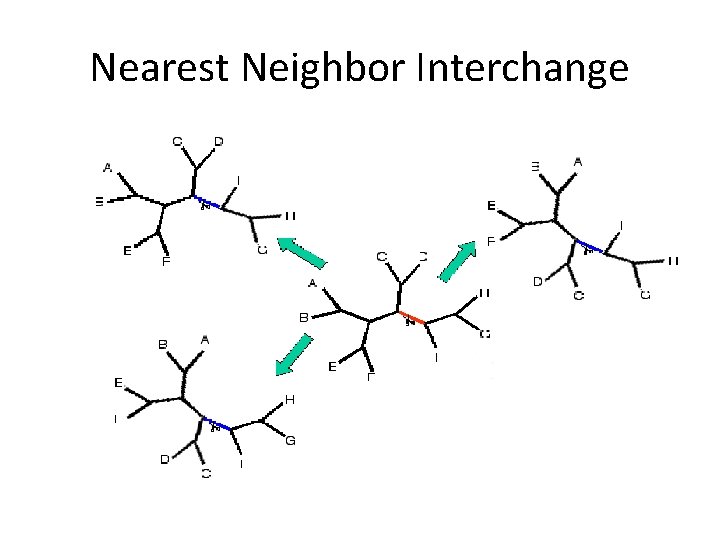
Nearest Neighbor Interchange • Start with an arbitrary tree and check its neighbors • Move to a neighbor if it provides the best improvement in parsimony score • No way of knowing if the result is the most parsimonious tree • Could be stuck in local optimum

Nearest Neighbor Interchange

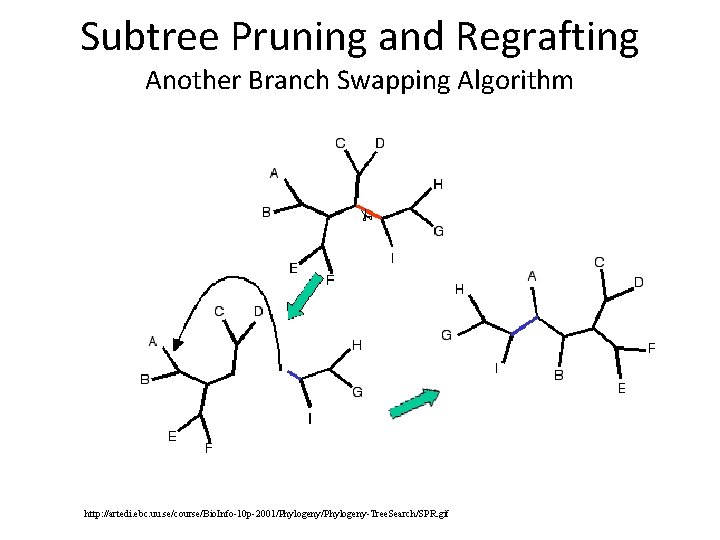
Subtree Pruning and Regrafting Another Branch Swapping Algorithm http: //artedi. ebc. uu. se/course/Bio. Info-10 p-2001/Phylogeny-Tree. Search/SPR. gif

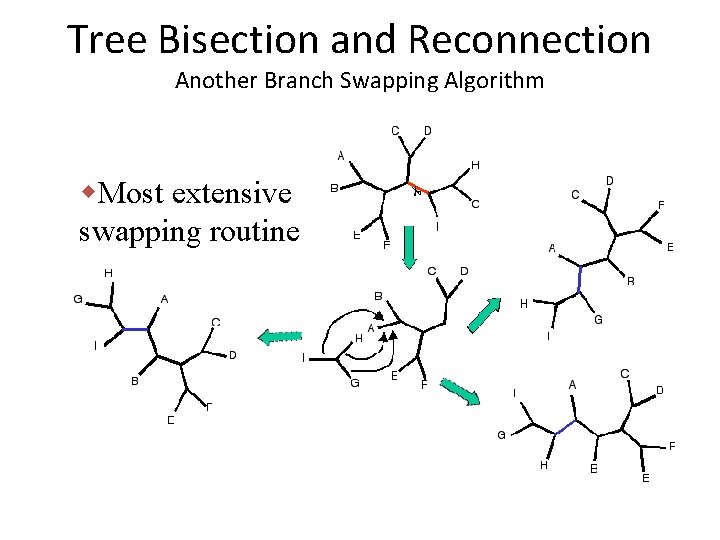
Tree Bisection and Reconnection Another Branch Swapping Algorithm w. Most extensive swapping routine

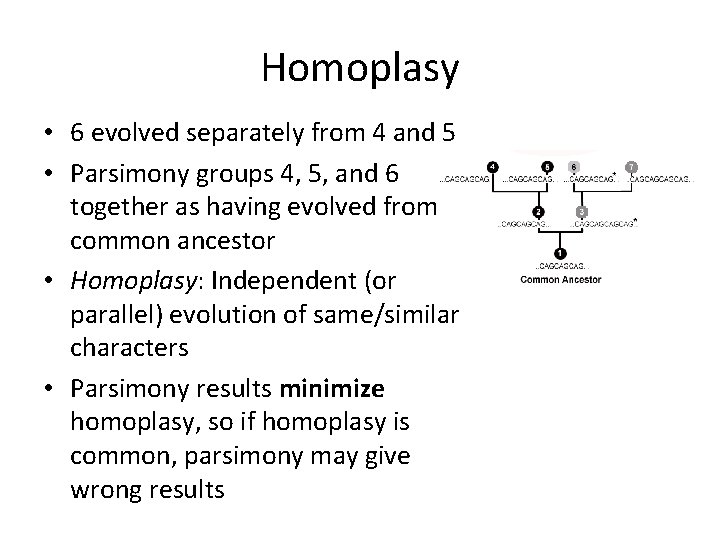
Homoplasy • Given: – – – – 1: CAGCAGCAG 2: CAGCAGCAG 3: CAGCAG 4: CAGCAGCAG 5: CAGCAGCAG 6: CAGCAGCAG 7: CAGCAG • Most would group 1, 2, 4, 5, and 6 as having evolved from a common ancestor, with a single mutation leading to the presence of 3 and 7

Homoplasy • But what if this was the real tree?

Homoplasy • 6 evolved separately from 4 and 5 • Parsimony groups 4, 5, and 6 together as having evolved from a common ancestor • Homoplasy: Independent (or parallel) evolution of same/similar characters • Parsimony results minimize homoplasy, so if homoplasy is common, parsimony may give wrong results

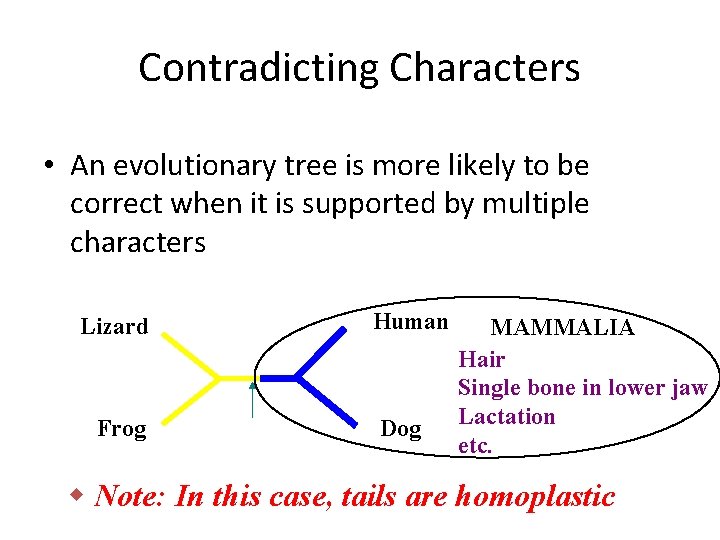
Contradicting Characters • An evolutionary tree is more likely to be correct when it is supported by multiple characters Lizard Frog Human Dog MAMMALIA Hair Single bone in lower jaw Lactation etc. w Note: In this case, tails are homoplastic

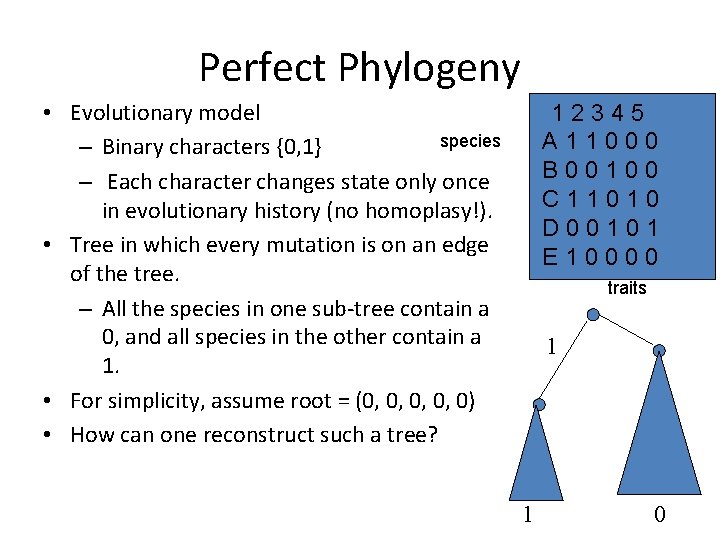
Perfect Phylogeny • Evolutionary model species – Binary characters {0, 1} – Each character changes state only once in evolutionary history (no homoplasy!). • Tree in which every mutation is on an edge of the tree. – All the species in one sub-tree contain a 0, and all species in the other contain a 1. • For simplicity, assume root = (0, 0, 0) • How can one reconstruct such a tree? 12345 A 11000 B 00100 C 11010 D 00101 E 10000 traits 1 1 0

The 4 -gamete condition • A column i partitions the set of species into two sets i 0, and i 1 • A column is homogeneous w. r. t a set of species, if it has the same value for all species. Otherwise, it is heterogeneous. • Example: i is heterogeneous w. r. t {A, D, E} i A 0 i 0 B 0 C 0 D 1 i 1 E 1 F 1

4 Gamete Condition There exists a perfect phylogeny if and only if for all pair of columns (i, j), j is homogenous w. r. t i 0 or i 1. Equivalently, There exists a perfect phylogeny if and only if for all pairs of columns (i, j), the following 4 rows do not exist i (0, 0), (0, 1), (1, 0), (1, 1) A 0 i 0 B 0 C 0 D 1 i 1 E 1 F 1

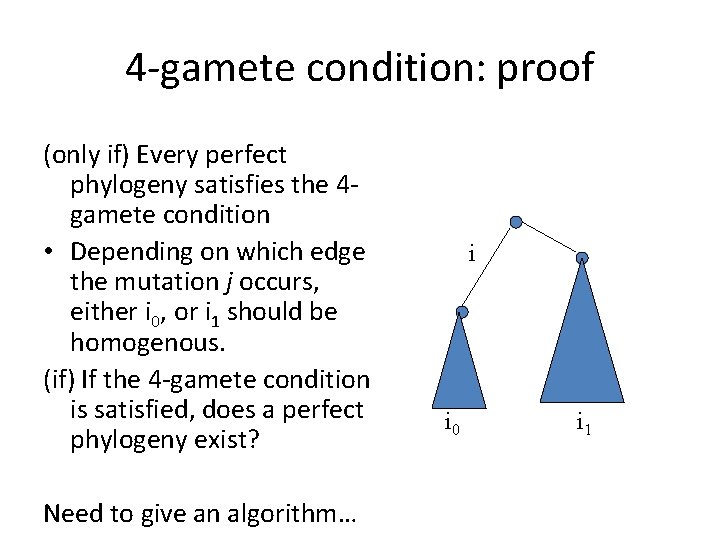
4 -gamete condition: proof (only if) Every perfect phylogeny satisfies the 4 gamete condition • Depending on which edge the mutation j occurs, either i 0, or i 1 should be homogenous. (if) If the 4 -gamete condition is satisfied, does a perfect phylogeny exist? Need to give an algorithm… i i 0 i 1

An algorithm for constructing a perfect phylogeny • We will consider the case where 0 is the ancestral state, and 1 is the mutated state. This will be fixed later. • In any tree, each node (except the root) has a single parent. – It is sufficient to construct a parent for every node. • In each step, we add a column and refine some of the nodes containing multiple children. • Stop if all columns have been considered.

Inclusion Property • For any pair of columns i, j: i < j if and only if i 1 j 1 • Note that if i < j then the edge containing i is an ancestor of the edge containing j i j

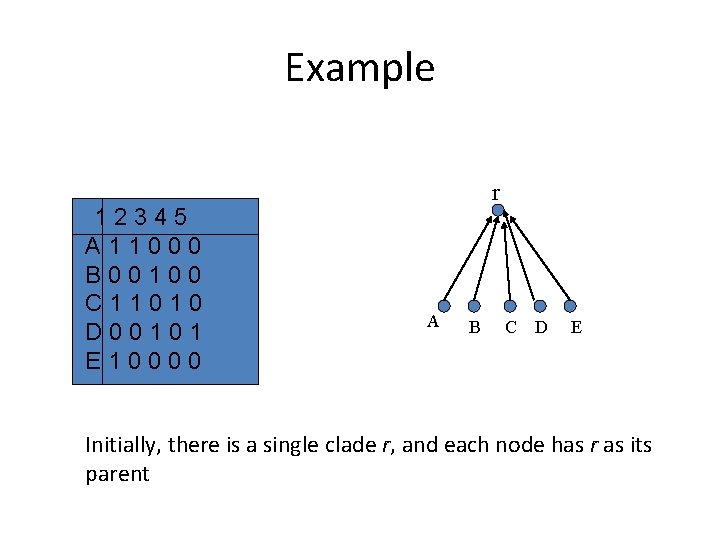
Example 12345 A 11000 B 00100 C 11010 D 00101 E 10000 r A B C D E Initially, there is a single clade r, and each node has r as its parent

Sort columns • Sort columns according to the inclusion property: i < j if and only if i 1 j 1 • This can be achieved by considering the columns as binary representations of numbers (most significant bit in row 1) and sorting in decreasing order 12345 A 11000 B 00100 C 11010 D 00101 E 10000

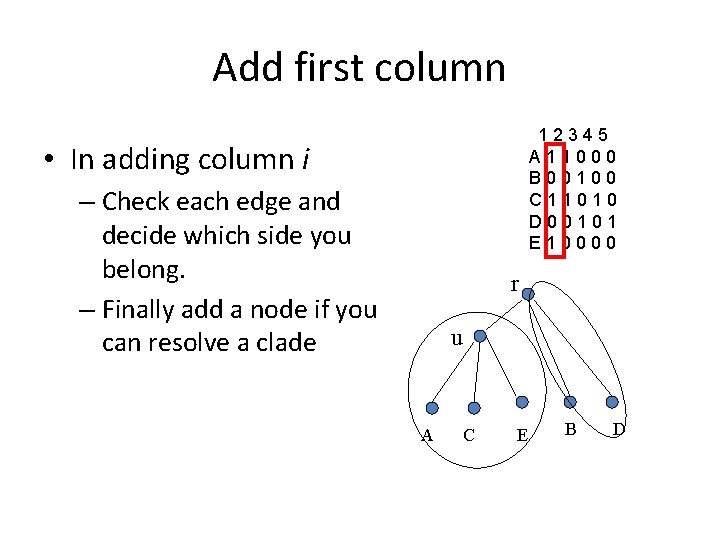
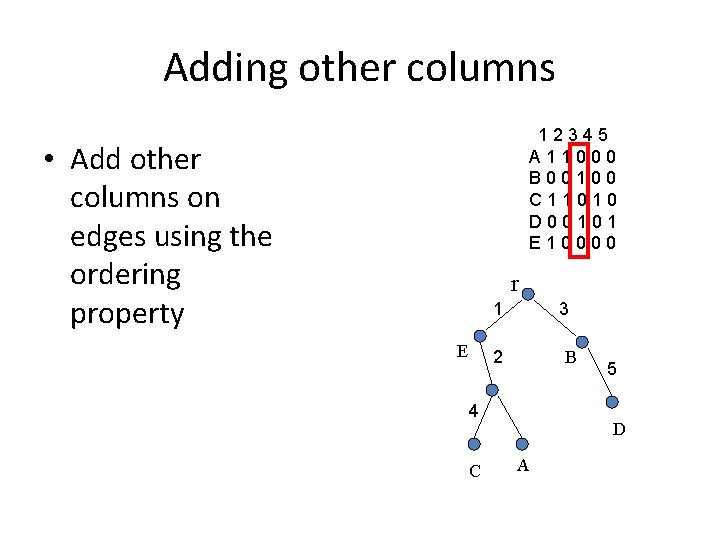
Add first column 12345 A 11000 B 00100 C 11010 D 00101 E 10000 • In adding column i – Check each edge and decide which side you belong. – Finally add a node if you can resolve a clade r u A C E B D

Adding other columns 12345 A 11000 B 00100 C 11010 D 00101 E 10000 • Add other columns on edges using the ordering property r 1 E 3 2 B 4 C 5 D A

Unrooted case • Switch the values in each column, so that 0 is the majority element. • Apply the algorithm for the rooted case

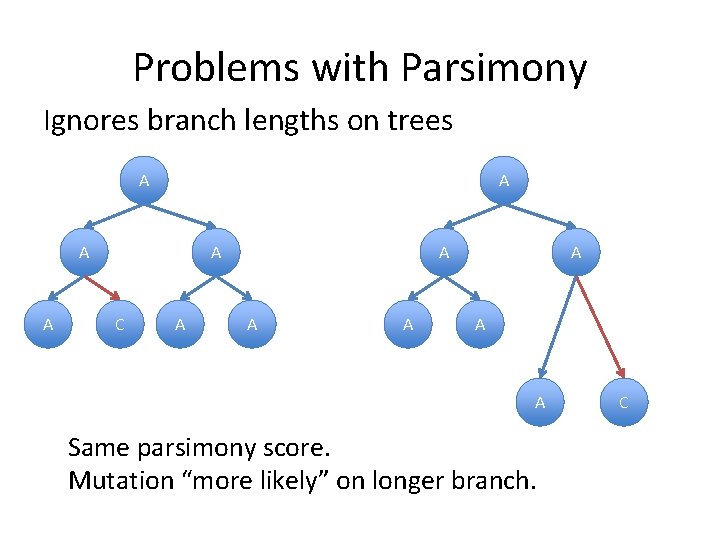
Problems with Parsimony Ignores branch lengths on trees A A A C A A A A Same parsimony score. Mutation “more likely” on longer branch. C

Maximum Likelihood See Class Notes

Algorithm Summary Distance based Parsimony Method Input Output Neighbor Joining Distance matrix D T, B UPGMA Distance matrix D T, B Sankoff’s & Fitch’s Alg. Characters, T A, B Perfect Phylogeny Characters A, B, T Characters, T, B A Probabilistic Felsenstein T = tree topology B = branch lengths A = ancestral states

Gene Tree vs. Species Tree

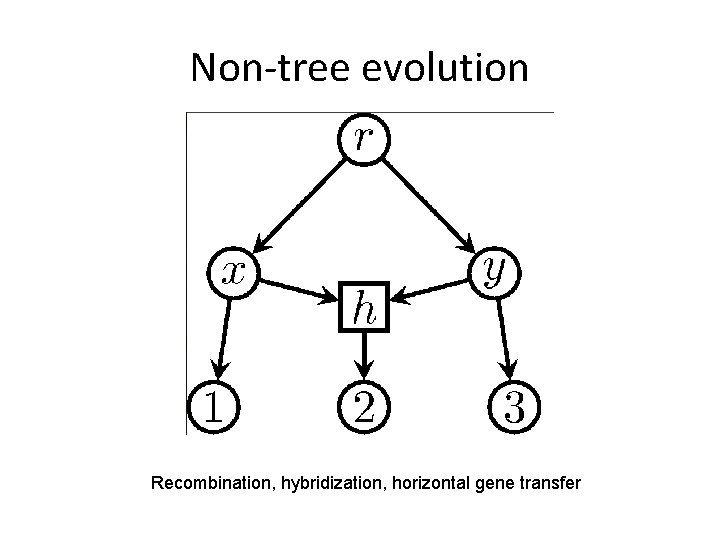
Non-tree evolution Recombination, hybridization, horizontal gene transfer

Using Multiple Methods • Important to keep in mind that reliance on purely one method for phylogenetic analysis provides incomplete picture • When different methods (parsimony, distance -based, etc. ) all give same result, more likely that the result is correct

How Many Times Evolution Invented Wings? • Whiting, et. al. (2003) looked at winged and wingless stick insects

Reinventing Wings • Previous studies had shown winged wingless transitions • Wingless winged transition much more complicated (need to develop many new biochemical pathways) • Used multiple tree reconstruction techniques, all of which required reevolution of wings

Most Parsimonious Evolutionary Tree of Winged and Wingless Insects • The evolutionary tree is based on both DNA sequences and presence/absence of wings • Most parsimonious reconstruction gave a wingless ancestor

Will Wingless Insects Fly Again? • Since the most parsimonious reconstructions all required the re-invention of wings, it is most likely that wing developmental pathways are conserved in wingless stick insects

Phylogenetic Analysis of HIV Virus • Lafayette, Louisiana, 1994 – A woman claimed her ex-lover (who was a physician) injected her with HIV+ blood • Records show the physician had drawn blood from an HIV+ patient that day • But how to prove the blood from that HIV+ patient ended up in the woman?

HIV Transmission • HIV has a high mutation rate, which can be used to trace paths of transmission • Two people who got the virus from two different people will have very different HIV sequences • Three different tree reconstruction methods (including parsimony) were used to track changes in two genes in HIV (gp 120 and RT)

HIV Transmission • Took multiple samples from the patient, the woman, and controls (non-related HIV+ people) • In every reconstruction, the woman’s sequences were found to be evolved from the patient’s sequences, indicating a close relationship between the two • Nesting of the victim’s sequences within the patient sequence indicated the direction of transmission was from patient to victim • This was the first time phylogenetic analysis was used in a court case as evidence (Metzker, et. al. , 2002)

Evolutionary Tree Leads to Conviction

Current popular methods HUNDREDS of programs available! http: //evolution. genetics. washington. edu/phylip/software. html#methods Some recommended programs: • Discrete—Parsimony-based – Rec-1 -DCM 3 http: //www. cs. utexas. edu/users/tandy/mp. html Tandy Warnow and colleagues • Probabilistic – SEMPHY http: //www. cs. huji. ac. il/labs/compbio/semphy/ Nir Friedman and colleagues

Sources • Metzker et al. Molecular evidence of HIV-1 transmission in a criminal case. PNAS 2002. • Whiting et al. “Loss and recovery of wings in stick insects” Nature 421, 264 -267 • Serafim Batzoglou http: //ai. stanford. edu/~serafim/CS 262_2006/ (Phylogeny slides) • http: //bioalgorithms. info (Phylogeny slides) • V. Bafna (Perfect Phylogeny slides)
 Compatibility
Compatibility Small parsimony problem
Small parsimony problem Maximum likelihood vs maximum parsimony
Maximum likelihood vs maximum parsimony Maximum likelihood vs maximum parsimony
Maximum likelihood vs maximum parsimony Maximum parsimony
Maximum parsimony 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Cleavage
Cleavage Molecular biology lectures
Molecular biology lectures Fibroblast
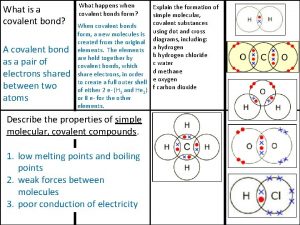
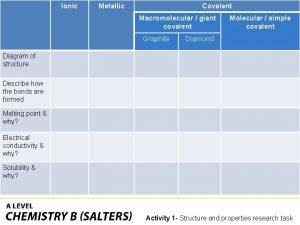
Fibroblast Giant molecular structure vs simple molecular structure
Giant molecular structure vs simple molecular structure Physical state of covalent compounds
Physical state of covalent compounds Giant molecular structure vs simple molecular structure
Giant molecular structure vs simple molecular structure Info 2950
Info 2950 Carla p gomes
Carla p gomes Cornell info 2950
Cornell info 2950 Cisco catalyst 2950 configuration
Cisco catalyst 2950 configuration Port security violation
Port security violation Giangarlo scientific
Giangarlo scientific Info 2950
Info 2950 Info 2950
Info 2950 Info 2950 cornell
Info 2950 cornell Info 2950
Info 2950 Dinosauria
Dinosauria Cladistics
Cladistics Outgroup in phylogeny
Outgroup in phylogeny Fish phylogeny
Fish phylogeny Ontogeny recapitulates phylogeny
Ontogeny recapitulates phylogeny Phylogeny and the tree of life chapter 26
Phylogeny and the tree of life chapter 26 Taxonomy of bacteria
Taxonomy of bacteria Cladogram animal kingdom
Cladogram animal kingdom Amphibian phylogeny
Amphibian phylogeny Cat family tree
Cat family tree Monophyletic group
Monophyletic group Ingroup phylogenetic tree
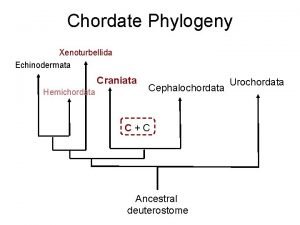
Ingroup phylogenetic tree Craniata
Craniata Chapter 26 phylogeny and the tree of life
Chapter 26 phylogeny and the tree of life What is a mammal
What is a mammal Basal group phylogeny
Basal group phylogeny Arthropoda phylogeny
Arthropoda phylogeny Ebi simple phylogeny
Ebi simple phylogeny Invertebrate phylogeny
Invertebrate phylogeny Protochordata
Protochordata Phylogeny is the study of _____.
Phylogeny is the study of _____. Chordates phylogenetic tree
Chordates phylogenetic tree Chapter 20 phylogeny and the tree of life
Chapter 20 phylogeny and the tree of life Phylogeny
Phylogeny What are nodes in a cladogram
What are nodes in a cladogram Chapter 26 phylogeny and the tree of life
Chapter 26 phylogeny and the tree of life Deer family tree
Deer family tree Metazoan phylogeny
Metazoan phylogeny Barnacle phylogeny
Barnacle phylogeny Chapter 26 phylogeny and the tree of life
Chapter 26 phylogeny and the tree of life Formal languages and automata theory tutorial
Formal languages and automata theory tutorial Csci3160
Csci3160 Mark redekopp
Mark redekopp Csci 5551
Csci 5551 Csci 3753
Csci 3753 Csci 530 security systems
Csci 530 security systems Csci 3753
Csci 3753 Csci-b 551 elements of artificial intelligence
Csci-b 551 elements of artificial intelligence Csci 5922
Csci 5922 201 principles of software development
201 principles of software development Csci 2670
Csci 2670 Csci 1933 umn
Csci 1933 umn Csci 420
Csci 420 Csci 3130
Csci 3130