CSCI 2950 C Lecture 6 Genome Rearrangements and

CSCI 2950 -C Lecture 6 Genome Rearrangements and Duplications http: //cs. brown. edu/courses/csci 2950 -c/

Outline 1. Recap • Sorting By Reversals & Breakpoint Graphs 2. Multichromosomal Rearrangements 3. Duplications: Segmental and Whole. Genome 4. Probabilistic Genome Rearrangements

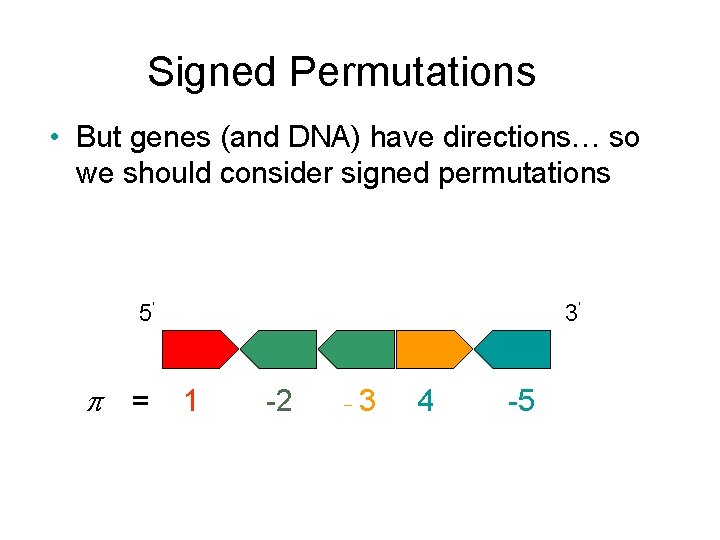
Signed Permutations • But genes (and DNA) have directions… so we should consider signed permutations 5’ p = 3’ 1 -2 - 3 4 -5

Sorting by reversals: 5 steps

Sorting by reversals: 4 steps

Sorting by reversals: 4 steps What is the reversal distance for this permutation? Can it be sorted in 3 steps?

Breakpoint graph 1 -dimensional construction n Transform = < 2, -4, -3, 5, -8, -7, -6, 1 > into = < 1, 2, 3, 4, 5, 6, 7, 8 > by reversals. n Vertices: i ® ia ib -i ® ib ia and 0 b, 9 a Edges: match the ends of consecutive blocks in , n Superimpose matchings n

Breakpoint graph Breakpoints Each reversal goes between 2 breakpoints, so d ³ # breakpoints / 2 = 6/2 = 3. n Theorem (Hannenhalli-Pevzner 1995): d(π) = n + 1 – c(π) + h(π) + f(π) where c(π) = # cycles; h, f are rather complicated, but can be computed from graph in polynomial time. n Here, d = 8 + 1 – 5 + 0 = 4 n

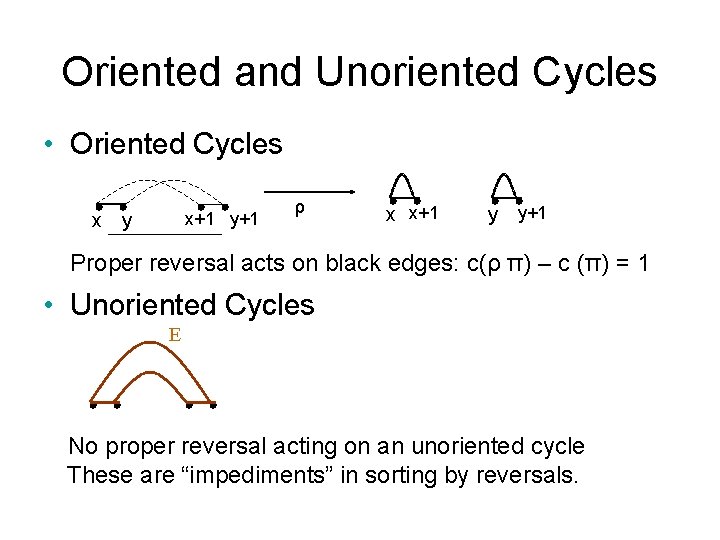
Oriented and Unoriented Cycles • Oriented Cycles x+1 y+1 x y ρ x x+1 y y+1 Proper reversal acts on black edges: c(ρ π) – c (π) = 1 • Unoriented Cycles E No proper reversal acting on an unoriented cycle These are “impediments” in sorting by reversals.

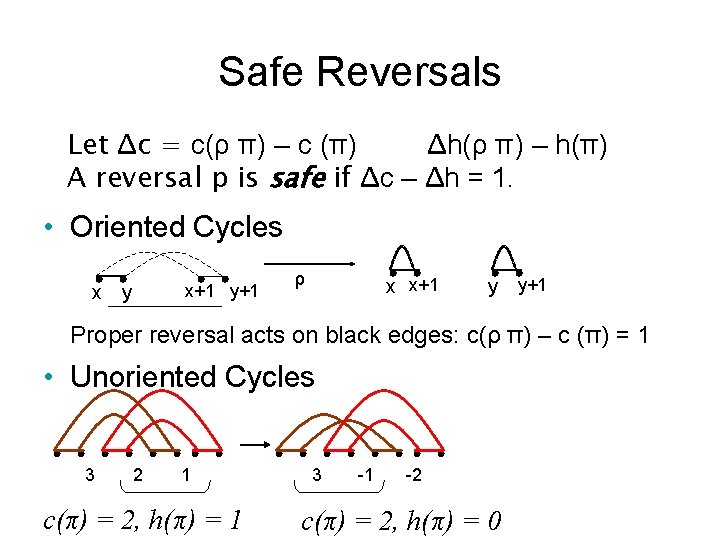
Safe Reversals Let Δc = c(ρ π) – c (π) Δh(ρ π) – h(π) A reversal p is safe if Δc – Δh = 1. • Oriented Cycles x+1 y+1 x y ρ x x+1 y y+1 Proper reversal acts on black edges: c(ρ π) – c (π) = 1 • Unoriented Cycles 3 2 1 c(π) = 2, h(π) = 1 3 -1 -2 c(π) = 2, h(π) = 0

Algorithm Outline Reversal_Sort(π) While π not sorted if π has a “long cycle” Select ρ [a padding of π] else if π has an oriented component Select a safe reversal in component else if π has a hurdle Select ρ [Hurdle merging or cutting] else if π is a fortress Select ρ [superhurdle merging] π π. ρ endwhile

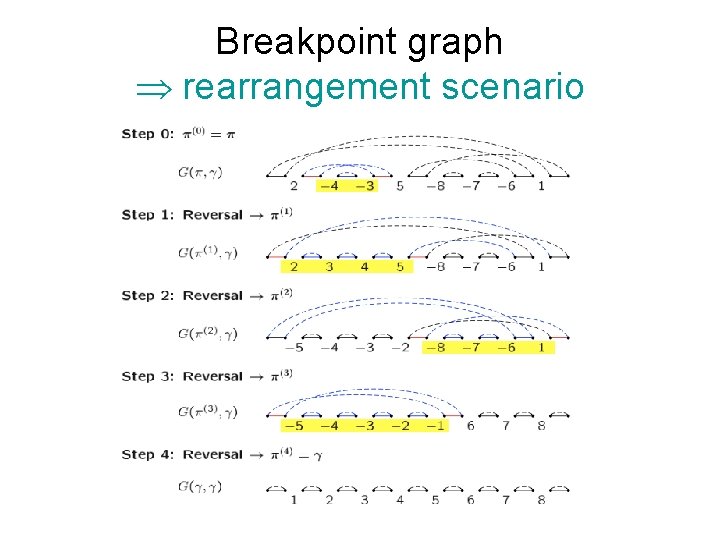
Breakpoint graph Þ rearrangement scenario

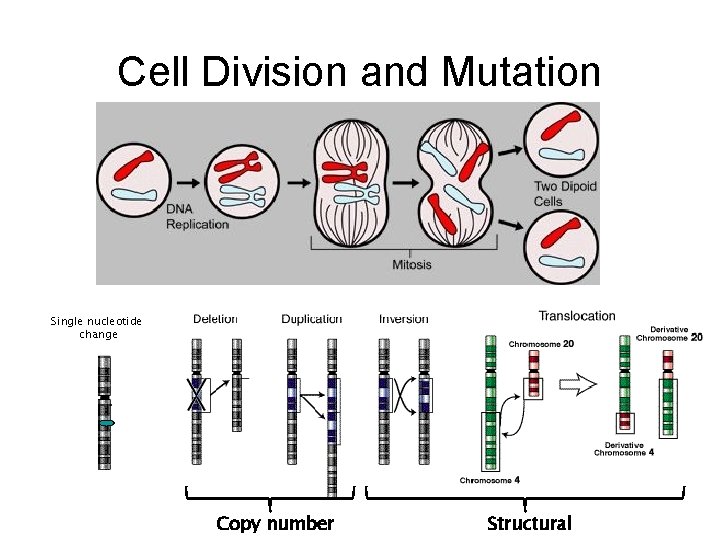
Cell Division and Mutation Single nucleotide change Copy number Structural

Types of Rearrangements Reversal 1 2 3 4 5 6 1 2 -5 -4 -3 6 Translocation 1 2 3 45 6 1 26 4 53 Fusion 1 2 3 4 5 6 Fission

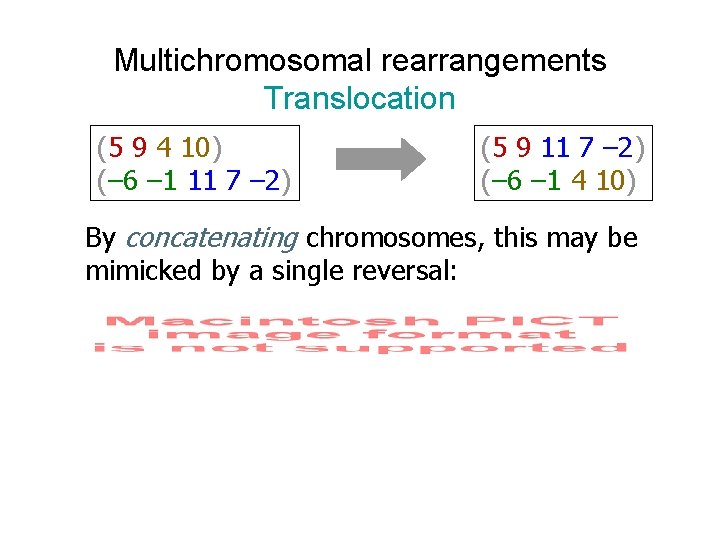
Multichromosomal rearrangements Translocation (5 9 4 10) (– 6 – 1 11 7 – 2) (5 9 11 7 – 2) (– 6 – 1 4 10) By concatenating chromosomes, this may be mimicked by a single reversal:

Multichromosomal rearrangements Translocation Most concatenates don’t work! n n n The first reversal just flipped a whole chromosome to position it correctly. This is an artifact of our genome representation; it is not a biological event. We want to avoid such artifacts.

Multichromosomal rearrangements Translocation Most concatenates don’t work! n n These concatenates required 3 reversals instead of 1! The second reversal just flipped a whole chromosome to position it correctly; this is an artifact of our genome representation, not a biological event. n We want to avoid such extra steps and artifacts.

Multichromosomal rearrangements Fission and fusion (1 2 3 4 5) () (1 2) (3 4 5) By concatenating chromosomes, this may be mimicked by a single reversal: Evolution: Human chromosome 2 is the fusion of two chromosomes from other hominoids (chimpanzees, orangutans, gorillas).

Multichromosomal rearrangements Fission and fusion (1 2 3 4 5) () (1 2) (3 4 5) • By concatenating chromosomes, this may be mimicked by a single reversal: • Flipping the whole chromosome (3 4 5) gives a different representation (– 5 – 4 – 3) of the same chromosome. • Chromosome ends ( ) must be tracked too.

Multichromosomal rearrangements Concatenates • Concatenate together all the chromosomes of a genome into a single sequence. • These concatenates represent the same genome: (5 9 4 10) (8 3) (– 6 – 1 11 7 – 2) (8 3) (2 – 7 – 11 1 6) (5 9 4 10) • Permuting the order of chromosomes and flipping chromosomes do not count as biological events. • Chromosome ends ( ) ( ) are included and are distinguishable.

Multichromosomal rearrangements Results Theorem (Tesler 2002): Let d = minimum total number of reversals, translocations, fissions, and fusions among all rearrangement scenarios between two genomes. By carefully choosing concatenates of the genomes, we can usually mimic a most parsimonious scenario by a d-step reversal scenario on the concatenates with no chromosome flips or chromosome permutations. There are pathological cases requiring a (d + 1)-step reversal scenario with one chromosome flip. Total time O(( n + N )2).

Multichromosomal rearrangements Results n n n = # of blocks, N = # of chromosomes Distance is the minimum number of reversals, fissions, fusions, translocations. Solution method: use suitable concatenates to obtain an equivalent “sorting by reversals” problem. The H-P algorithm has a nonconstructive step that required a lot of work to fix. It pertains to choosing concatenates to avoid flips and chromosome permutations. (Tesler 2002) does this constructively.

GRIMM Web Server • Real genome architectures are represented by signed permutations • Efficient algorithms to sort signed permutations have been developed • GRIMM web server computes the reversal distances between signed permutations:

GRIMM Web Server 22 dense pages to fix gaps http: //www-cse. ucsd. edu/groups/bioinformatics/GRIMM

Other Types of Rearrangements • Transpositions 123456 125346 • Duplication Transposition 123456 12345346 Duplications are very frequent in cancer genomes.

Duplications What problem to solve? Given G {1, . . , n}N. i = (1 2 … n) (“permutation with duplicates”) Find reversals 1, 2, …, t, duplications 1, …, s, and permutation such that ( 1, …, t, 1, …, s) i = G and s + t is minimal 123456 ? ? ? 1 2 3 4 5 3 4 -2 -3 6 HARD!!! (NP-hard? )

Duplications (2) What problem to solve? Given: G {1, . . , n}N , H = G for permutation , (“permutation with duplicates”) Find: Reversals 1, 2, …, t such that 1 … t G = H and t is minimal Signed reversal distance with duplicates NP-hard (Chen, et al. 2005) If 1 -1 mapping of repeated elements (orthologs) in G to H then problem reduces to reversal distance.

Duplications (3) What problem to solve? Given: G {1, . . , n}N (permutation with duplicates) Find: Permutation , reversals 1, 2, …, s, and duplications 1, … t such that 1, …, s 1, …, t = G and t minimal. Solution when at most two duplicates per gene and restricted class of duplications El-Mabrouk and Sankoff (2002)

Whole Genome Duplication • Genome is doubled – extra copy of each element. • Subsequently undergoes reversals. Genome Halving Problem. Given a duplicated genome P, recover the ancestral pre-duplicated genome R minimizing the reversal distance from the perfect duplicated genome R R to the duplicated genome P. (El-Mabrouk and Sankoff 1998 -2003)

Whole Genome Duplication • Genome is doubled – extra copy of each element. • Subsequently undergoes reversals. If copies of each element labeled uniquely, then problem reduces to reversal distance problem.

Reversal Distance and Duplications • Let d(G, H) = reversal distance b/w G and H • Problem of computing d(P, R R) is unsolved • min. R d(P, R R) solvable in polynomial time

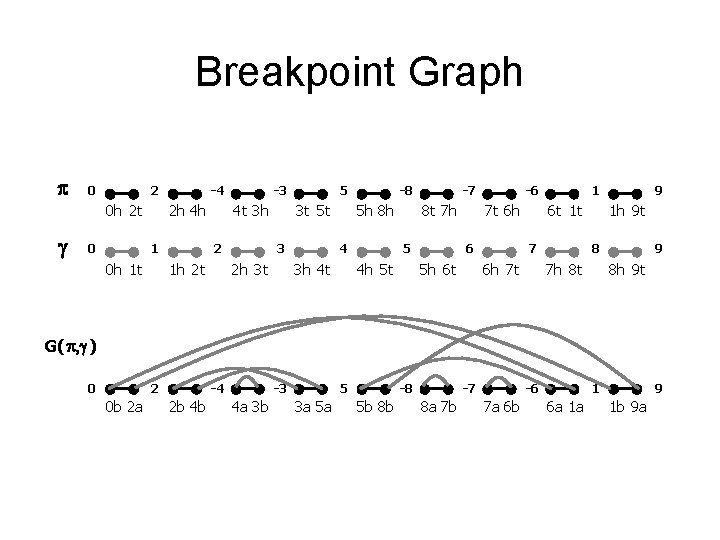
Breakpoint Graph p 0 2 0 h 2 t g 0 -4 2 h 4 h 1 0 h 1 t -3 4 t 3 h 2 1 h 2 t 5 3 t 5 t 3 2 h 3 t -8 5 h 8 h 4 3 h 4 t -7 8 t 7 h 5 4 h 5 t -6 7 t 6 h 6 5 h 6 t 1 t 7 6 h 7 t 9 1 h 9 t 8 7 h 8 t 9 8 h 9 t G( p, g ) 0 2 0 b 2 a -4 2 b 4 b -3 4 a 3 b 5 3 a 5 a -8 5 b 8 b -7 8 a 7 b -6 7 a 6 b 1 6 a 1 a 9 1 b 9 a

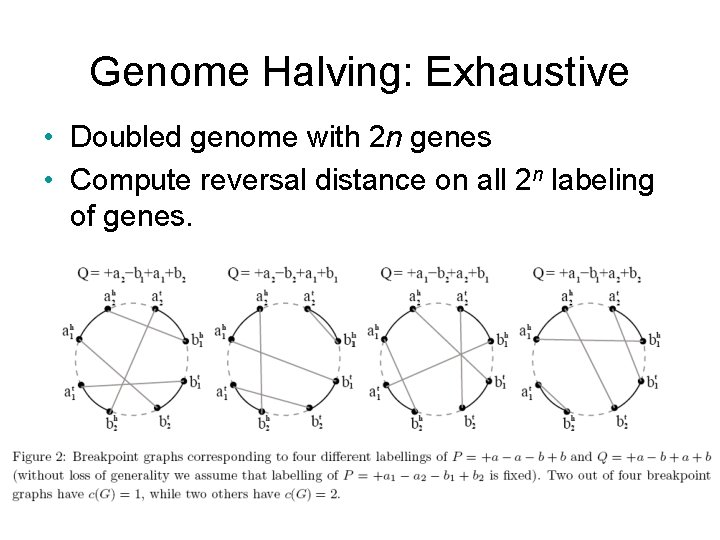
Genome Halving: Exhaustive • Doubled genome with 2 n genes • Compute reversal distance on all 2 n labeling of genes.

Genome Halving • Weak Genome Halving Problem. For a given duplicated genome P, find a perfect duplicated genome R R and a labeling of gene copies that maximizes the number of black-gray cycles c(G) in the breakpoint graph G(P, R R) of the labeled genomes P and R R. (Alekseyev and Pevzner 2006) Theorem (Hannenhalli-Pevzner 1995): d(π) = n + 1 – c(π) + h(π) + f where c = # cycles; h = # hurdles f = 1 if π is fortress.

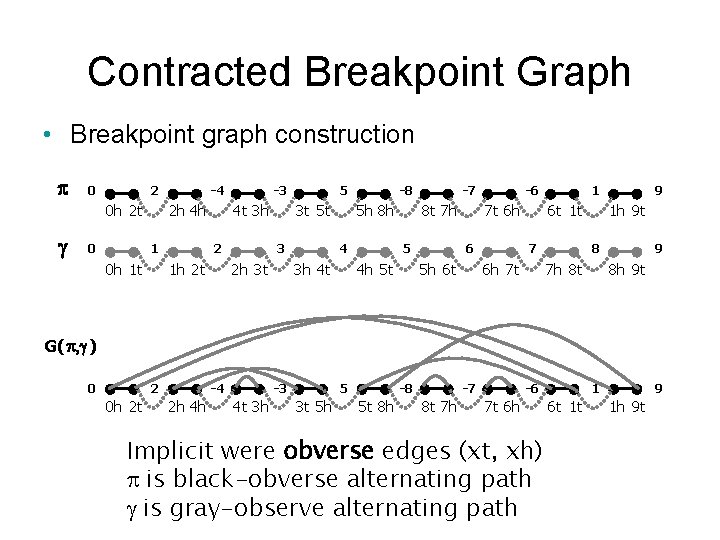
Contracted Breakpoint Graph • Breakpoint graph construction p 0 2 0 h 2 t g 0 -4 2 h 4 h 1 0 h 1 t -3 4 t 3 h 2 1 h 2 t 5 3 t 5 t 3 2 h 3 t -8 5 h 8 h 4 3 h 4 t -7 8 t 7 h 5 4 h 5 t -6 7 t 6 h 6 5 h 6 t 1 t 7 6 h 7 t 9 1 h 9 t 8 7 h 8 t 9 8 h 9 t G( p, g ) 0 2 0 h 2 t -4 2 h 4 h -3 4 t 3 h 5 3 t 5 h -8 5 t 8 h -7 8 t 7 h -6 7 t 6 h Implicit were obverse edges (xt, xh) is black-obverse alternating path is gray-observe alternating path 1 6 t 1 t 9 1 h 9 t

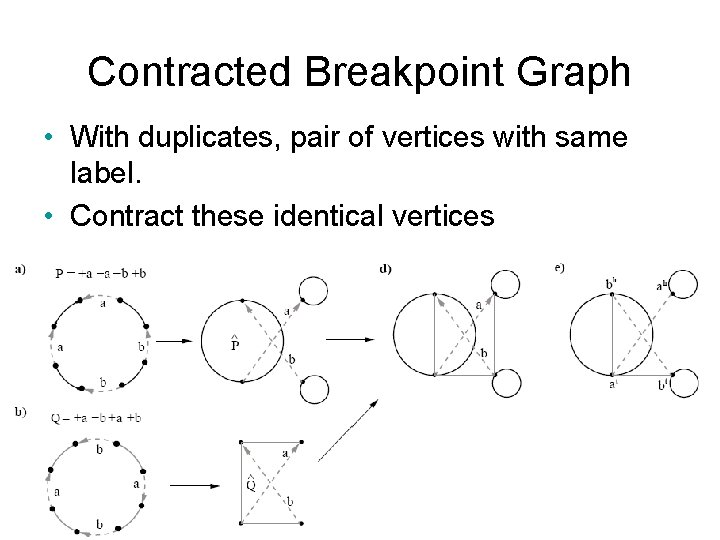
Contracted Breakpoint Graph • With duplicates, pair of vertices with same label. • Contract these identical vertices

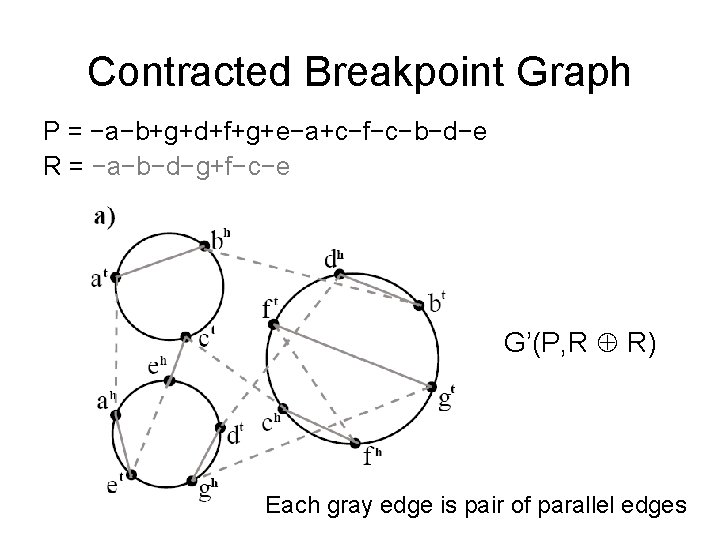
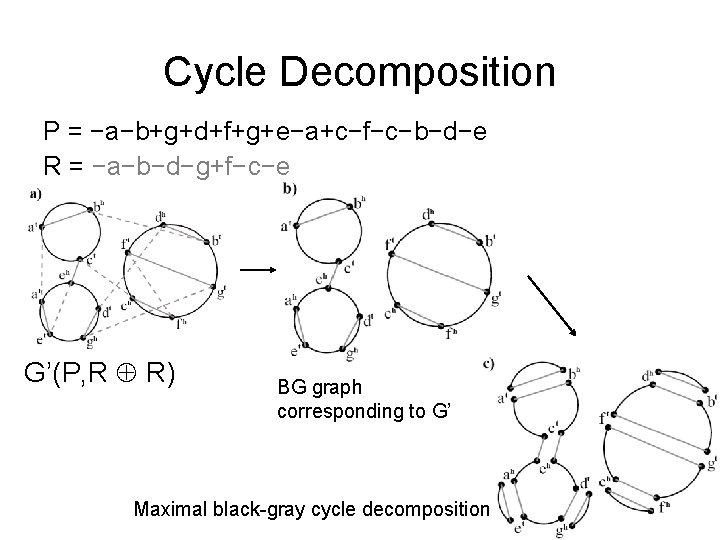
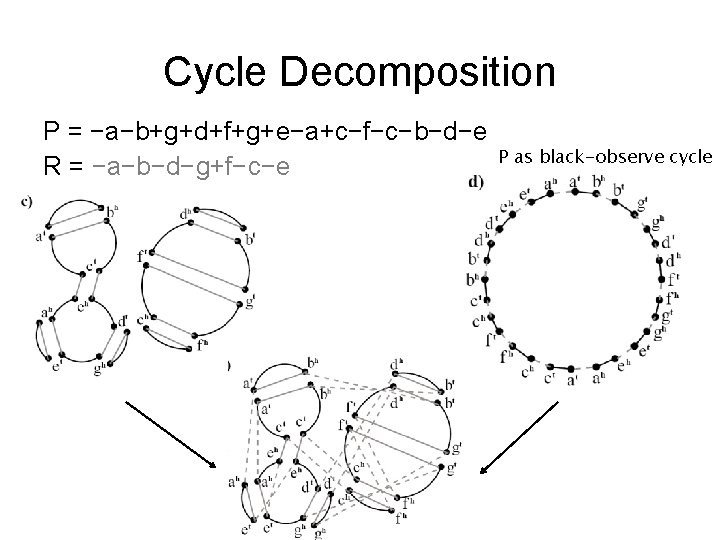
Contracted Breakpoint Graph P = −a−b+g+d+f+g+e−a+c−f−c−b−d−e R = −a−b−d−g+f−c−e G’(P, R R) Each gray edge is pair of parallel edges

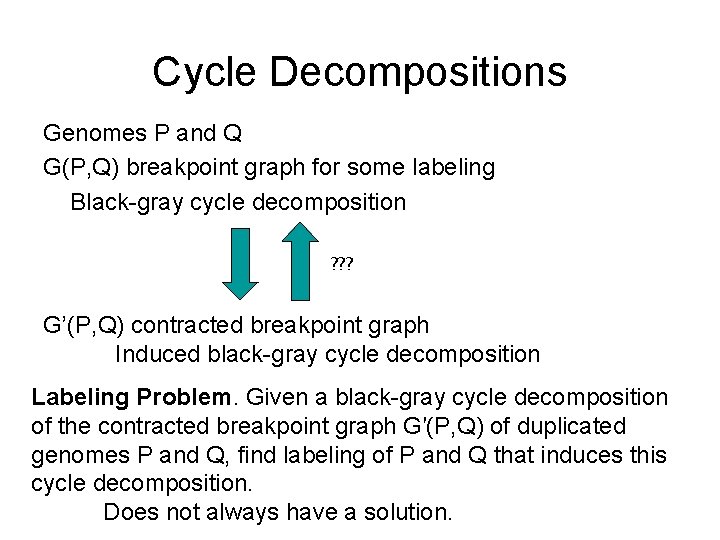
Cycle Decompositions • In H-P theory, c(π) = # of cycles in maximal cycle decomposition was key parameter. • Strategy: analyze cycle decompositions of contracted breakpoint graph

Cycle Decompositions Genomes P and Q G(P, Q) breakpoint graph for some labeling Black-gray cycle decomposition ? ? ? G’(P, Q) contracted breakpoint graph Induced black-gray cycle decomposition Labeling Problem. Given a black-gray cycle decomposition of the contracted breakpoint graph G′(P, Q) of duplicated genomes P and Q, find labeling of P and Q that induces this cycle decomposition. Does not always have a solution.

Cycle Decomposition P = −a−b+g+d+f+g+e−a+c−f−c−b−d−e R = −a−b−d−g+f−c−e G’(P, R R) BG graph corresponding to G’ Maximal black-gray cycle decomposition

Cycle Decomposition P = −a−b+g+d+f+g+e−a+c−f−c−b−d−e R = −a−b−d−g+f−c−e P as black-observe cycle

Genome Halving Algorithm: Outline Input: Doubled genome P 1. Construct BO (black-obverse) graph for P by gluing identical edges 2. Introduce gray edges “optimally” to create BOG (black-observe-gray) graph G’ with single gray-observe cycle (!!!) 3. R = gray-observe cycle in G’ 4. Find maximal black-gray cycle decomposition of G’ and labeling of 5. Q = R R

Alternative Rearrangement Metrics • Thus far, distance posed as minimum number of rearrangements transforming one permutation to identity. • Parsimony assumption in evolution. • Score S(ρ) for a rearrangement ρ. • Parsimony: S(ρ) = 1 for all ρ. S(ρ1, ρ2 …, ρt� ) = Σ S(ρi) = t • Length-weighted reversals S(ρ) = l(ρ)α, where l(ρ) = length of reversed subsequence (Bender, et al. 2008) Many of the resulting optimization problems are NP hard

Probabilistic Genome Rearrangements • Pr[rearrangement ρ] = p. Compute Pr[rearrangement sequence ρ1…ρn] • Inversions occur according to Poisson process (York, et al. (2002)) • L inversions: Pr[L | λ] = e-λ λL / L! • n(n+1)/2 possible inversions. • Each occurs with equal probability • Ω = {inversion sequences} • For X = ρ1… ρLx ε Ω, Pr[X | λ] = (e-λ λLx / Lx!) ( n (n+1)/2)-Lx

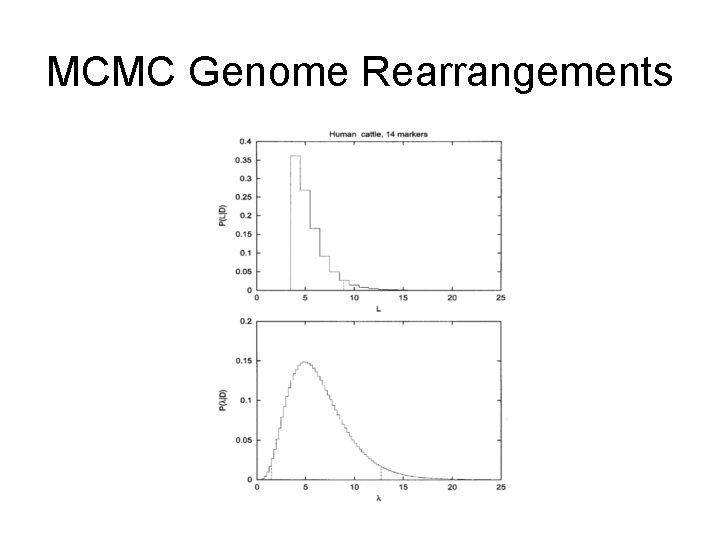
Probabilistic Genome Rearrangements • Pr[X, λ | π] = Pr [X, λ, π] / Pr[π] = Pr[π | X, λ] Pr[X | λ] Pr[λ] / Pr[π] = (1) ((e-λ λLx / Lx!) ( n (n+1)/2)-Lx) (1/ λmax) / Pr[π] • Problem: How to evaluate this distribution? • Solution: Iteratively sample from Ω × (0, λmax]. • (X 0, λ 0) (X 1, λ 1) (X 2, λ 2) … • After a long time, reach stationary distribution. • Markov chain Monte Carlo

MCMC Genome Rearrangements • How to update? (Xi, λi) (Xi+1, λi+1) • Alternate updates of λ and X (Metropolis-Hastings algorithm) • (Xi, λi) (Xi, λi+1) (Xi+1, λi+1) • Pr[ λ | X, π] α Pr[X | λ] Pr[λ] α e-λ λLx Pr[λ]

MCMC Genome Rearrangements: Updating X (Xi, λi+1) (Xi+1, λi+1) 1. Choose a section to replace with probability q(l, j), l = length, pj = starting permutation 2. Generate new subpath from pα to pβ • Use breakpoint graph G(pα, pβ) to choose an inversion sequence where Δ(c) = 1 with high probability

MCMC Genome Rearrangements

MCMC Genome Rearrangements • Can we use this approach for other genome rearrangement operations? • Translocations, duplications, etc.

References • • G. Tesler: “Efficient algorithms for multichromosomal genome rearrangements. ” J. Comput. Syst. Sci. 65(3): 587 -609 (2002) Xin Chen, Jie Zheng, Zheng Fu, Peng Nan, Yang Zhong, Stefano Lonardi, Tao Jiang: Assignment of Orthologous Genes via Genome Rearrangement. IEEE/ACM Trans. Comput. Biology Bioinform. 2(4): 302 -315 (2005) N. El-Mabrouk: “Reconstructing an ancestral genome using minimum segments duplications and reversals. ” J. Comput. Syst. Sci. 65(3): 442 -464 (2002) N. El-Mabrouk, David Bryant, David Sankoff: “Reconstructing the predoubling genome. ” RECOMB 1999: 154 -163 M. Alekseyev & P. Pevzner: “Colored de Bruijn Graphs and the Genome Halving Problem. ” IEEE/ACM Trans. Comput. Biology Bioinform. 4(1): 98107 (2007) Bender, et al. “Improved bounds on sorting by length-weighted reversals. ” J. of Computer and System Sciences 74 (2008) 744– 774. York, et al. “Bayesian Estimation of the Number of Inversions in the History of Two Chromosomes” J. of Computational Biol. (2002)