CSCI 256 Data Structures and Algorithm Analysis lecture

CSCI 256 Data Structures and Algorithm Analysis lecture 1 Some slides by Kevin Wayne copyright 2005, Pearson Addison Wesley all rights reserved, and some by Iker Gondra

Course Overview • MSCS Dept webpage: CS 256 http: //www. sites. stfx. ca/mscs/CS 256

Algorithms • Algorithm – [webster. com] A procedure for solving a mathematical problem (as of finding the greatest common divisor) in a finite number of steps that frequently involves repetition of an operation – [Knuth, TAOCP] An algorithm is a finite, definite, effective procedure, with some input and some output Great algorithms are the poetry of computation. Just like verse, they can be terse, allusive, dense, and even mysterious. But once unlocked, they cast a brilliant new light on some aspect of computing. - Francis Sullivan

Theory of Algorithms "As soon as an Analytic Engine exists, it will necessarily guide the future course of the science. Whenever any result is sought by its aid, the question will arise - By what course of calculation can these results be arrived at by the machine in the shortest time? - Charles Babbage

Theory of Algorithms • Claim: All* of Computer Science is the study of algorithms • What constitutes expertise in this area? • How do experts differ from novices? – Partial answer – there is a difference between doing something and doing it well – we strive to do it well (eg: guarantee correctness every time termination, scalability (at least for well described subclass of problems)

The Algorithmic Enterprise • The algorithmic enterprise consists of two fundamental components: – the task of getting to the mathematically clean core of a problem, and then – the task of identifying the appropriate algorithm design techniques, based on the structure of the problem.

Course Goals • Goal: To convey the algorithmic approach as a design process that: – begins with problems arising across the full range of computing applications, – builds on an understanding of algorithm design techniques, and – results in the development of efficient solutions to these problems. • The material and our discussions in this course will be structured around a sequence of three steps: – Describing a problem and working out its precise (clean mathematical) formulation; – Employing an appropriate design technique to develop an algorithm; – Proving properties of the algorithm (including its correctness) and analyzing its efficiency.

Algorithmic Paradigms • Design and analysis of computer algorithms – – – Greed Divide-and-conquer Dynamic programming Network flow Intractability Coping with intractability

A First Problem: Stable Matching • Setting: – Assign TAs to Instructors – Avoid having TAs and Instructors wanting to change • E. g. , Prof A. would rather have student X than her current TA, and student X would rather work for Prof A. than his current instructor

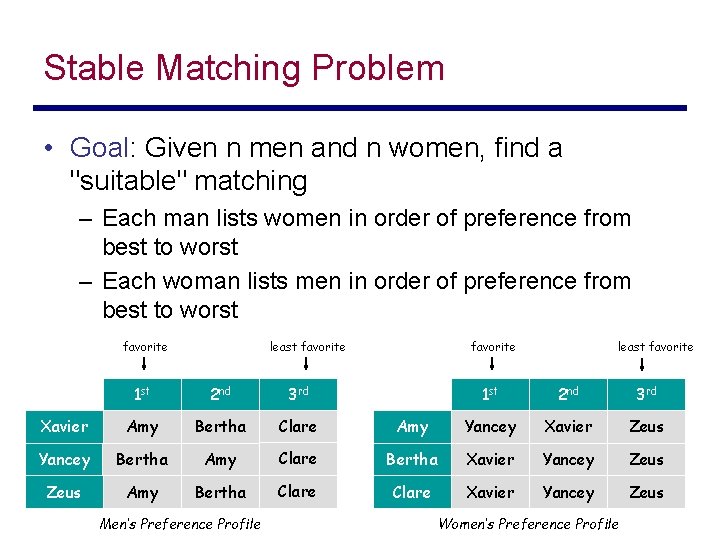
Stable Matching Problem • Goal: Given n men and n women, find a "suitable" matching – Each man lists women in order of preference from best to worst – Each woman lists men in order of preference from best to worst favorite least favorite 1 st 2 nd 3 rd Xavier Amy Bertha Clare Yancey Bertha Amy Zeus Amy Bertha Men’s Preference Profile favorite least favorite 1 st 2 nd 3 rd Amy Yancey Xavier Zeus Clare Bertha Xavier Yancey Zeus Clare Xavier Yancey Zeus Women’s Preference Profile

Stable Matching Problem • Perfect matching: everyone is matched monogamously – Each man gets exactly one woman – Each woman gets exactly one man • Instability: incentive for some pair of participants to undermine assignment by joint action – In matching M, a pair m-w is unstable if man m and woman w prefer each other over their current partners

Stable Matching Problem • Stable matching: perfect matching with no unstable pairs • Stable matching problem: Given the preference lists of n men and n women, find a stable matching if one exists

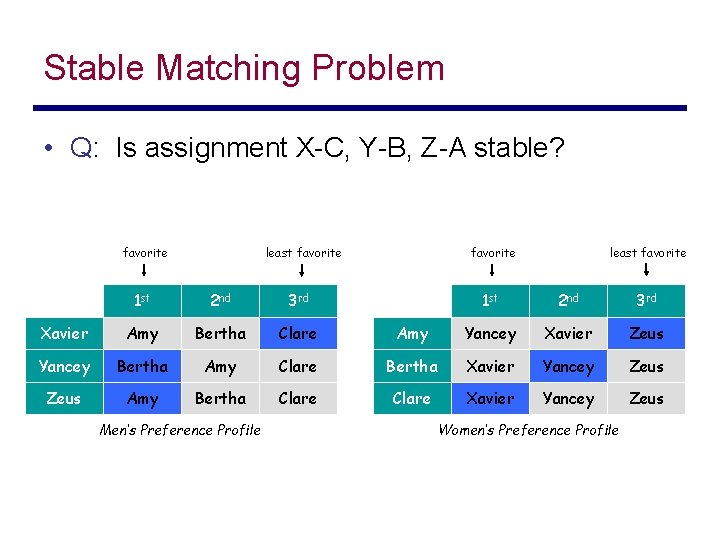
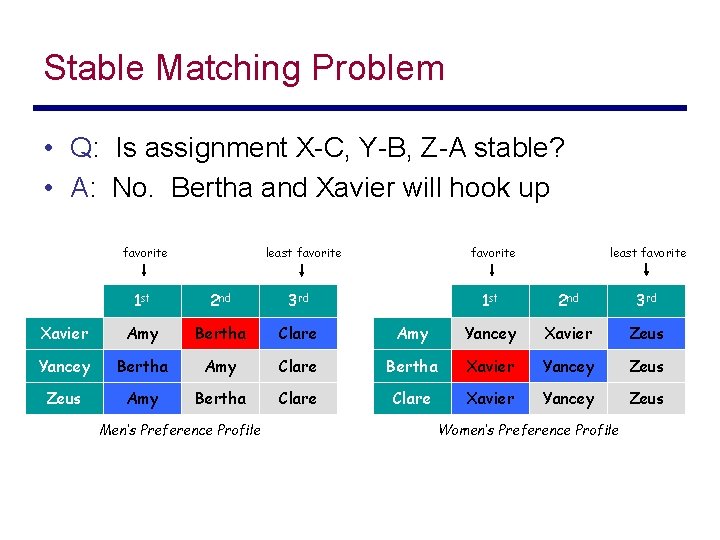
Stable Matching Problem • Q: Is assignment X-C, Y-B, Z-A stable? favorite least favorite 1 st 2 nd 3 rd Xavier Amy Bertha Clare Yancey Bertha Amy Zeus Amy Bertha Men’s Preference Profile least favorite 1 st 2 nd 3 rd Amy Yancey Xavier Zeus Clare Bertha Xavier Yancey Zeus Clare Xavier Yancey Zeus Women’s Preference Profile

Stable Matching Problem • Q: Is assignment X-C, Y-B, Z-A stable? • A: No. Bertha and Xavier will hook up favorite least favorite 1 st 2 nd 3 rd Xavier Amy Bertha Clare Yancey Bertha Amy Zeus Amy Bertha Men’s Preference Profile least favorite 1 st 2 nd 3 rd Amy Yancey Xavier Zeus Clare Bertha Xavier Yancey Zeus Clare Xavier Yancey Zeus Women’s Preference Profile

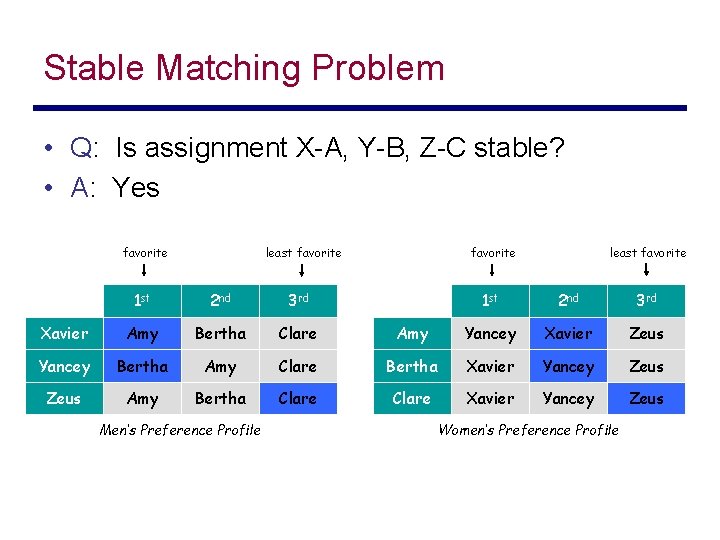
Stable Matching Problem • Q: Is assignment X-A, Y-B, Z-C stable? • A: Yes favorite least favorite 1 st 2 nd 3 rd Xavier Amy Bertha Clare Yancey Bertha Amy Zeus Amy Bertha Men’s Preference Profile least favorite 1 st 2 nd 3 rd Amy Yancey Xavier Zeus Clare Bertha Xavier Yancey Zeus Clare Xavier Yancey Zeus Women’s Preference Profile

Example – stable matching everyone gets first choice • • m 1 : w 1 w 2 m 2 : w 2 w 1: m 1 m 2 w 2: m 2 m 1 w 1 m 2 w 2

Example: unique stable matching • • m 1 : w 1 w 2 m 2 : w 1 w 2 w 1: m 1 m 2 w 2: m 1 m 2 m 1 w 1 m 2 w 2

2 stable matchings • • m 1 : w 1 w 2 m 2 : w 2 w 1: m 2 m 1 w 2: m 1 m 2 both men are as happy as possible; or both women are as happy as possible

Example: can you find a stable matching? (Exercise for the student!) m 1 : w 1 w 2 w 3 m 1 w 1 m 2 w 2 m 3 w 3 m 2 : w 1 w 3 w 2 m 3 : w 1 w 2 w 3 w 1: m 2 m 3 m 1 w 2: m 3 m 1 m 2 w 3: m 3 m 1 m 2

Indicators of Stable Matching Problem • Want Perfect matching • Have Preference lists (ranking is strictly increasing) • Want Stability – Instable (dotted line: m 1 and w 2 prefer each other) m 1 w 1 m 2 w 2

Intuitive Idea for a Proposal Algorithm • m proposes to w – If w is unmatched, w accepts – If w is matched to m' • If w prefers m to m', w accepts • If w prefers m' to m, w rejects • Unmatched m proposes to w highest on its preference list that m has not already proposed to

Propose-And-Reject Algorithm • Propose-and-reject algorithm [Gale-Shapley 1962]: Intuitive method that guarantees output which is a stable matching Initialize each person to be free while (some man is free and hasn't proposed to every woman) { Choose such a man m w = 1 st woman on m's list to whom m has not yet proposed if (w is free) assign m and w to be engaged else if (w prefers m to her fiancé m') assign m and w to be engaged, and m' to be free else w rejects m }

Example m 1 : w 1 w 2 w 3 m 1 w 1 m 2 w 2 m 3 w 3 m 2 : w 1 w 3 w 2 m 3 : w 1 w 2 w 3 w 1: m 2 m 3 m 1 w 2: m 3 m 1 m 2 w 3: m 3 m 1 m 2

Does this Work? • • • Does it terminate? Is the result a stable matching? Is the solution unique? What is the complexity? To analyse, we begin by identifying measures of progress and invariants: – Observation 1: Men propose to women in decreasing order of preference – Observation 2: Once a woman is matched, she never becomes unmatched; she only “trades up. ”