Csci 136 Computer Architecture II Lab6 Arithmetic Operations

Csci 136 Computer Architecture II Lab#6 Arithmetic Operations HW #5: Due on Mar. 1, before class Feb. 23, 2005

Unsigned Multiplication - Shift Multiplicand Left n Example: q q 4 -bit register 0010*0011 n n n Multiplicand: 8 bits Multiplier: 4 bits Product: 8 bits

Unsigned Multiplication - Shift Multiplicand Left Multiplier Multiplicand Product 0011 0000 0010 0000 • Initial 0011 0000 0010 • Prod+Mcand 0011 0000 0100 0010 • Mcand 0001 0000 0100 0010 • Mier 0001 0000 0100 0000 0110 0001 0000 1000 0110 …. …… …… • Cost ? ? ? • Time • Space

Unsigned Multiplication - Shift Product Right n Observations: q q q n Work on one bit each time 1/2 bits in multiplicand always 0 least significant bits of product never changed once formed Save Space? q Example: n n 4 -bit register 0010*0011 q q q n Multiplicand: 4 bits Multiplier: N/A Product: 8 bits Save Time? M’cand=0010 Product=0000 0011

Signed Multiplication n Booth’s algorithm Inspected bits 2 k+1 2 2 k-1 Operation 0 0 0 Shift right 2 bits 0 0 1 +1 x m’cand, shift right 2 bits 0 1 0 +1 x m’cand, shift right 2 bits 0 1 1 +2 x m’cand, shift right 2 bits 1 0 0 -2 x m’cand, shift right 2 bits 1 0 1 -1 x m’cand, shift right 2 bits 1 1 0 -1 x m’cand, shift right 2 bits 1 1 1 Shift right 2 bits

Booth’s algorithm n Example: q M’cand =3 = 0011 n q -m’cand=1101 M’ier = -2 = 1110

Unsigned Division - Restoring Division Start: Place Dividend in Remainder 1. Subtract the Divisor register from the Remainder register, and place the result in the Remainder register. Remainder 0 2 a. Shift the Quotient register to the left setting the new rightmost bit to 1. Test Remainder < 0 2 b. Restore the original value by adding the Divisor register to the Remainder register, & place the sum in the Remainder register. Also shift the Quotient register to the left, setting the new least significant bit to 0. 3. Shift the Divisor register right 1 bit. 33 repetition? No: < 33 repetitions Yes: 33 repetitions Done
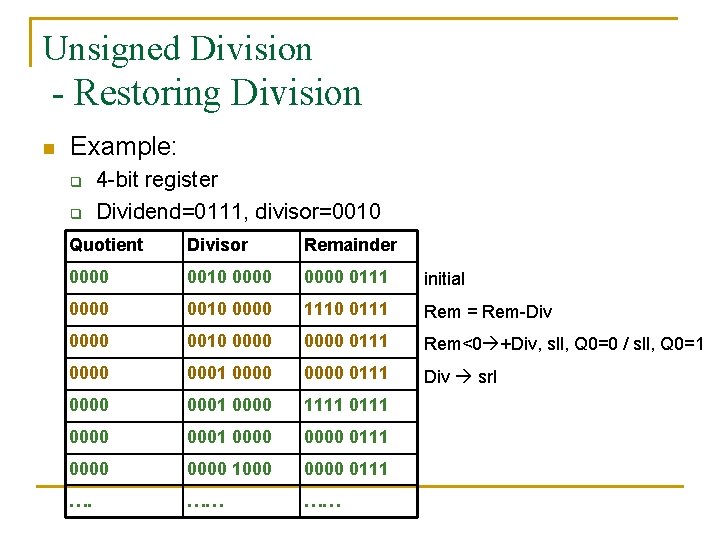
Unsigned Division - Restoring Division n Example: q q 4 -bit register Dividend=0111, divisor=0010 Quotient Divisor Remainder 0000 0010 0000 0111 initial 0000 0010 0000 1110 0111 Rem = Rem-Div 0000 0010 0000 0111 Rem<0 +Div, sll, Q 0=0 / sll, Q 0=1 0000 0111 Div srl 0000 0001 0000 1111 0000 0001 0000 0111 0000 1000 0111 …. …… ……

Floating-point Representation n n IEEE 754 Standard (-1)S x (1 + Significand) x 2(Exponent-127) q Double precision identical, except with exponent bias of 1023 31 30 23 22 S Exponent 1 bit 8 bits Significand 23 bits 0

Decimal Floating-point Representation n Example: -0. 375 q q q -0. 375 = -3/8 -11 two/1000 two = -0. 011 two Normalized to -1. 1 two x 2 -2 (-1)S x (1 + Significand) x 2(Exponent-127) (-1)1 x (1 +. 100 0000. . . 0000) x 2(125 -127) 1 0111 1101 100 0000 0000

Floating-point Representation Decimal n Example: 1 10000001 010 0000 0000 q (-1)S x (1 + Significand) x 2(Exponent-127) q (-1)1 x (1 + 0. 25) x 2(129 -127)

Floating-point Addition n Example: 0. 5 ten + -0. 4375 ten q q 0. 5 ten = 1/2 ten = 1. 000 two x 2 -1 -0. 4375 ten = -7/16 ten = -1. 110 two x 2 -2 q Alignment: -1. 110 two x 2 -2 = -0. 111 two x 2 -1 1. 000 two x 2 -1 +(-0. 111 two x 2 -1) = 0. 001 two x 2 -1 Normalization: 0. 001 two x 2 -1 = 1. 000 two x 2 -4 Rounding: 4 -bit already q 1. 000 two x 2 -4 = 0. 0625 q q q

Floating-point Multiplication n Example: 0. 5 ten x -0. 4375 ten q q q q 0. 5 ten = 1/2 ten = 1. 000 two x 2 -1 -0. 4375 ten = -7/16 ten = -1. 110 two x 2 -2 Exponents: (-1+127)+(-2+127)-127 = 124 Significands: 1. 000 twox 1. 110 two=1. 110000 twox 2 -3 Normalization: -126≤exp. ≤ 127 Rounding: =1. 110 twox 2 -3 Sign: -1. 110 twox 2 -3

HW#5 n Example: q 0111/0011: quotient=0010, remainder=0001 n Difference? n Restoring Division: q n (Remainder+Divisor)*2 – Divisor Non-restoring Division: q Remainder*2 + Divisor
- Slides: 14