CSCE 355 Foundations of Computation Lecture 1 Overview

CSCE 355 Foundations of Computation Lecture 1 Overview Topics 1. n June 1, 2015 Proof techniques: induction, contradiction Proof techniques

Models of Computation – 2– CSCE 355 Summer 2015

Course Outcomes • Mathematical prerequisites: functions, relations, properties of relations, posets. • Proof Techniques • Finite automata: regular languages, regular expressions, DFAs, NFAs, equivalences. • Limitations: pumping lemma • Context free languages: grammars, push-down automata • Turing machines: undecidability, the halting problem • Intractability: NP, NP-Completeness – 3– CSCE 355 Summer 2015

Prerequisites • CSCE 211 Number systems, n Boolean algebra, n logic design, n sequential machines n l Mealy machines l Moore machines – 4– CSCE 355 Summer 2015

Prerequisites • CSCE 350 Techniques for representing and processing information, including the use of n lists, trees, and graphs; n n n – 5– analysis of algorithms; sorting, searching, and hashing techniques. • MATH 374 Propositional and predicate logic; n proof techniques; n recursion and recurrence relations; n sets, n combinatorics, n n and probability; n functions, relations, n and matrices; n algebraic structures. CSCE 355 Summer 2015

Review of Relations on Sets • Binary relations - (X, Y) ἐ R or X Rel Y n n < on integers likes (X, Y) • Unary relation - properties n boring(matthews) • Ternary relation – 6– n “X was introduced to Y by Z” -- ( X, Y, Z) n Table in a relational database CSCE 355 Summer 2015

Special types of Relations • Injections • Surjections • Functions – 7– CSCE 355 Summer 2015

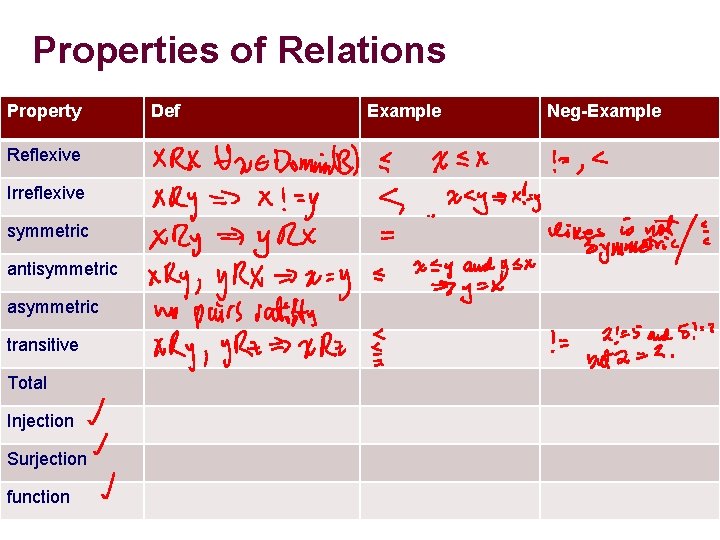
Properties of Relations Property Def Example Neg-Example Reflexive Irreflexive symmetric antisymmetric asymmetric transitive Total Injection Surjection function – 8– CSCE 355 Summer 2015

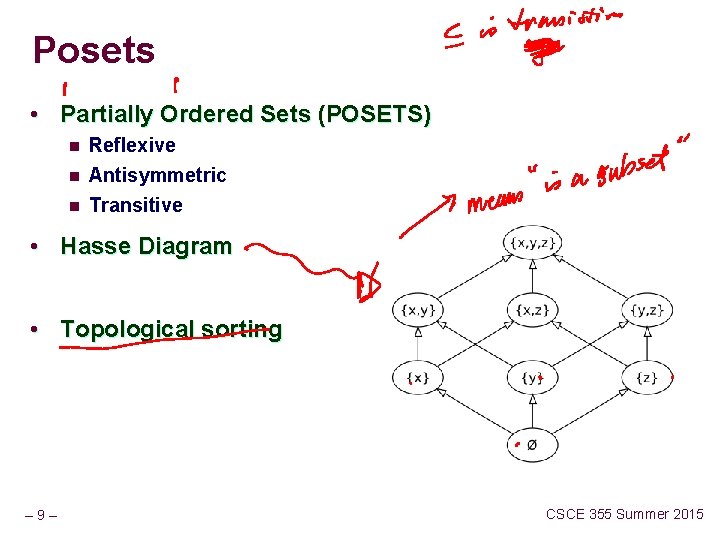
Posets • Partially Ordered Sets (POSETS) n Reflexive n Antisymmetric Transitive n • Hasse Diagram • Topological sorting – 9– CSCE 355 Summer 2015

Equivalence relations – 10 – CSCE 355 Summer 2015

Proof Techniques n 1. 1 Direct proof n 1. 2 Proof by induction 1. 3 Proof by transposition 1. 4 Proof by contradiction 1. 5 Proof by construction 1. 6 Proof by exhaustion 1. 7 Probabilistic proof 1. 8 Combinatorial proof 1. 9 Nonconstructive proof 1. 10 Proof nor disproof 1. 11 Elementary proof n n n n n – 11 – CSCE 355 Summer 2015

Deductive Proofs the conclusion is established by logically combining the axioms, definitions, and earlier theorems Example: The sum of two even integers is even. Hypothesis – 12 – CSCE 355 Summer 2015

Theorem 1. 3 used to prove Theorem 1. 4 • Theorem 1. 3 If x >= 4 then 2 x >= x 2. • Theorem 1. 4 If x is the sum of the squares of 4 positive integers then 2 x >= x 2. • Proof – 13 – CSCE 355 Summer 2015

Theorem 1. 3 If x >= 4 then 2 x >= x 2. • f(x) = x 2 / 2 x. • Then what is the derivative f’ of f • Derivative of quotient? ? n http: //www. math. hmc. edu/calculus/tutorials/quotient_rule/ • So f’(x) = – 14 – CSCE 355 Summer 2015

Proofs about Equality of Sets • To prove S = T n Show S is a subset of T, and n T is a subset of S • Commutative law of union • Theorem 1. 10 Distributive law of union over intersection • Proof – 15 – CSCE 355 Summer 2015

Proof by Contradiction – 16 – CSCE 355 Summer 2015

If and only If statements • IF H then C n H implies C n H only if C C if H n H = Hypothesis C = conclusion • A if and only if B n n If part : Only-if part • Theorm 1. 7 ceiling = floor x is an integer – 17 – CSCE 355 Summer 2015

Induction • Given a statement S(n) about an integer n that we want to prove. • Basis Step: Show S(i) is true for a particular integer i n Usually i = 0 or i = 1 • Inductive Step: Assume S(n) is true for n >= i and then show S(n+1) is true • Inductive Hypothesis: Assume S(n) is true – 18 – CSCE 355 Summer 2015

Example Induction Proof: Theorem 1. 16 – 19 – CSCE 355 Summer 2015

Number of leaves in complete tree of height h is 2 h. – 20 – CSCE 355 Summer 2015

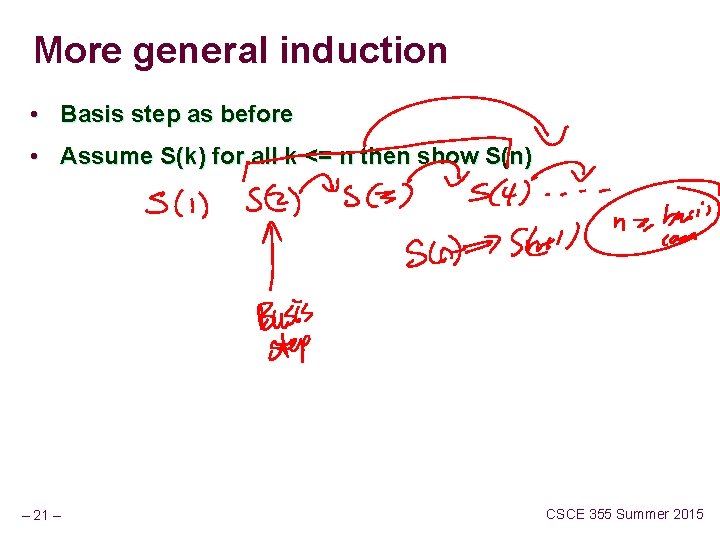
More general induction • Basis step as before • Assume S(k) for all k <= n then show S(n) – 21 – CSCE 355 Summer 2015

Recursive Def of Tree • Basis: a single node is a tree. • If T 1, T 2, … Tk are trees then a new tree can be formed by 1. 2. 3. – 22 – Add new node N, the root of the new tree Add copies of T 1… Tk Add an edge from N to the root of each T 1, T 2, … Tk CSCE 355 Summer 2015

Structural Induction • For objects with recursive definitions consisting of base objects and then combining rules • Basis step: show the proposition S(X) holds for every base object X. • Inductive step: Given a recursive structure X formed from X 1, X 2, … Xn by the application of the def. then Assume S(X 1) S(X 2) …. S(Xn) are true and show that S(X) is true – 23 – CSCE 355 Summer 2015

Recursive Def of Arithmetic Expressions • Basis: a number or a variable is an expression. • If E and F are expressions then a new expression G can be formed by applying one of the three rules 1. G = E + F 2. G = E * F 3. G = ( E ) – 24 – CSCE 355 Summer 2015

Every Expression has equal number of left and right parenthses – 25 – CSCE 355 Summer 2015

Homework 1. . 2. Prove if a complete binary tree has n leaves then it has 2 n-1 nodes. – 26 – CSCE 355 Summer 2015

References– Mathematical Foundations • http: //en. wikipedia. org/wiki/Binary_relation • http: //en. wikipedia. org/wiki/Relation_(mathematics) • http: //en. wikipedia. org/wiki/Mathematical_proof • http: //en. wikipedia. org/wiki/Proofs_from_THE_BOOK Extended “Proof” techniques • http: //www. maths. uwa. edu. au/~berwin/humour/invalid. proofs. html Fair Use Books Online • http: //fair-use. org/bertrand-russell/the-principles-ofmathematics/ Books Dr. Euler's Fabulous Formula: Cures Many Mathematical CSCE 355 Summer 2015 – 27 – Ills