CSCE 350 Algorithms and Data Structure Lecture 5

CSCE 350 Algorithms and Data Structure Lecture 5 Jianjun Hu Department of Computer Science and Engineering University of South Carolina 2009. 9.

Outline q How to analyze the Time Efficiency of non-recursive algorithms q How to analyze time efficiency of recursive algorithms

Analyze the Time Efficiency of An Algorithm Nonrecursive Algorithm Recursive Algorithm

Element Uniqueness Check whether all the elements in a given array are distinct Input: An array A[0…n-1] Output: Return “true” if all the elements in A are distinct and “false” otherwise

Selection sort

Insertion Sort

Insert Sorting—running time cases § The best case input is an array that is already sorted. In this case insertion sort has a linear running time (i. e. , O(n)). During each iteration, the first remaining element of the input is only compared with the right-most element of the sorted subsection of the array. § The worst case input is an array sorted in reverse order. In this case every iteration of the inner loop will scan and shift the entire sorted subsection of the array before inserting the next element. For this case insertion sort has a quadratic running time (i. e. , O(n 2)). § The average case is also quadratic, which makes insertion sort impractical for sorting large arrays. However, insertion sort is one of the fastest algorithms for sorting arrays containing fewer than ten elements.

Improvement of Insert sorting § Shell sort: two simple variants requiring O(n 3/2) and O(n 4/3) running time. § binary insertion sort § In 2004 Bender, Farach-Colton, and Mosteiro published a new variant of insertion sort called library sort or gapped insertion sort high probability in O(n log n) time

Example: Find the Number of Binary Digits in the Binary Representation of a Positive Decimal Integer

How to identify inefficiency and speed it up? What is it doing? Time complexity? How to speed it up?

How to identify inefficiency and speed it up? 2. 4. 7 Matrix multiplication For i 0 to n-1 do for j 0 to n-1 do C[i, j] 0 for k 0 to n-1 do C[i, j]+A[i, k]*B[k, j]

Example Recursive evaluation of n ! Recursive algorithm for n! Input size: n Basic operation: multiplication “*” Let M(n) be the number of multiplications needed to compute n!, then To compute Factorial(n-1) To multiply Factorial(n-1) by n

Solve the Recurrence Therefore, the number of multiplications needed to compute n! in this algorithm is n. The complexity of this algorithm is

Time Efficiency of Recursive Algorithms Steps in mathematical analysis of recursive algorithms: Decide on parameter n indicating input size Identify algorithm’s basic operation Determine worst, average, and best case for input of size n Set up a recurrence relation and initial condition(s) for C(n)-the number of times the basic operation will be executed for an input of size n (alternatively count recursive calls). Solve the recurrence to obtain a closed form or

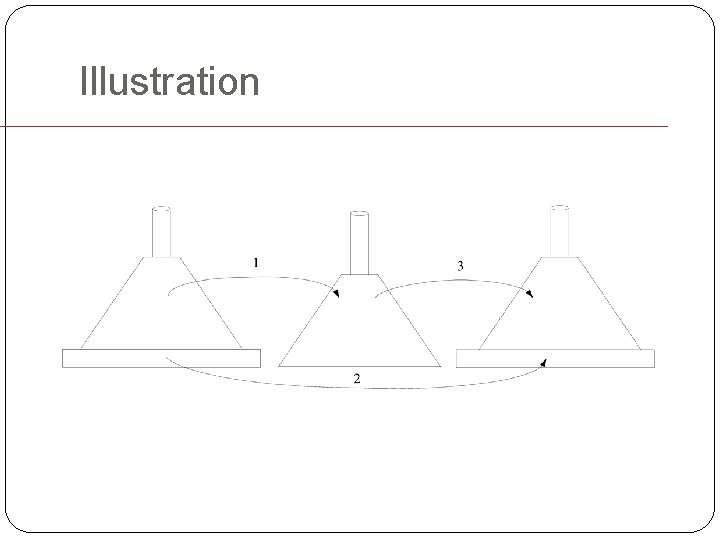
Another Example: Tower of Hanoi n different-size disks, 3 pegs, move disks from the left peg to the right one using the middle one as an auxiliary Rules: you can move one disk each time and it is forbidden to place a larger disk on top of a smaller one Design and algorithm and analyze its complexity

Recursive Algorithm Input size: n (disks) Basic operation: one move of a disk Initial condition: n=1 only one direct move To build the recurrence: suppose you have a way to move n-1 disks. Then you can move the top n-1 disks from the left peg to the middle peg using the right peg as an auxiliary. Move the bottom disk from the left peg to the right peg. Move n-1 disks from the middle peg to the right peg using the left one as an auxiliary.

Illustration

Algorithm Complexity Let M(n) be the number of needed moves Initialization M(1)=1 Recurrence

Important Recurrence Types: One (constant) operation reduces problem size by one. T(n) = T(n-1) + c T(1) = d Solution: T(n) = (n-1)c + d linear A pass through input reduces problem size by one. T(n) = T(n-1) + cn T(1) = d Solution: T(n) = [n(n+1)/2 – 1] c + d quadratic One (constant) operation reduces problem size by half. T(n) = T(n/2) + c Solution: T(n) = c lg n + d T(1) = d logarithmic A pass through input reduces problem size by half. T(n) = 2 T(n/2) + cn T(1) = d Solution: T(n) = cn lg n + d n n log n

A General Divide-and-Conquer Recurrence: Master Theorem T(n) = a. T(n/b) + f (n) where f (n) ∈ Θ(nk) a < bk T(n) ∈ Θ(nk) a = bk T(n) ∈ Θ(nk lg n ) a > bk T(n) ∈ Θ(nlog b a) Note: the same results hold with O instead of Θ.

Binary Digits (Recursive Algorithm) Find the Number of Binary Digits in the Binary Representation of a Positive Decimal Integer using a recursive algorithm Recurrence