CSCE 212 H Computer Architecture Lecture 1 Introduction

CSCE 212 H Computer Architecture Lecture 1 Introduction to Computer Architecture Topics n Representations of Data n Computer Architecture C Programming Unsigned Integers Signed magnitude Two’s complement n n January 16, 2018

Course Pragmatics Syllabus n Instructor: Manton Matthews n Website: http: //www. cse. sc. edu/~matthews/Courses/212/index. html n Text l "Computer Systems: A Programmer's Perspective" 3 rd edition by Randal E. Bryant and David O'Hallaron, Prentice-Hall 2016. – 2– n Important Dates on website n Academic Integrity n Slides are based on text, some directly supplied by the authors CSCE 212 H Spring 2018

What is Computer Architecture? Computer Architecture is the attributes of a [computing] system as seen by the programmer, i. e. the conceptual structure and functional behavior, as distinct from the organization of the data flows and controls the logic design, and the physical implementation. – Amdahl, Blaaw, and Brooks, 1964 The term computer architecture was first used in 1964 the designers of the IBM System/360. The IBM/360 was a family of computers all with the same architecture, but with a variety of organizations(implementations). – 3– CSCE 212 H Spring 2018

What and Why for this course Architecture from the programmer perspective n Use knowledge of architecture to improve performance Topics n n n n Representations of Data Basic Computer Organization Instruction Set Design Pipelining HDL Memory Hierarchies Basics of Performance Evaluation Interconnection Basics The goal is to provide foundational knowledge in the structure and organization of machines to enable you to write better programs – 4– CSCE 212 H Spring 2018

Umax, Tmin, Max Float Unsigned Two’s complement Floats Doubles – 5– CSCE 212 H Spring 2018

Carnegie Mellon Great Reality #1: Ints are not Integers, Floats are not Reals Example 1: Is x 2 ≥ 0? n Float’s: Yes! n Int’s: l 40000 * 40000 ➙ 1, 600, 000 l 50000 * 50000 ➙ ? ? Example 2: Is (x + y) + z = x + (y + z)? n n Unsigned & Signed Int’s: Yes! Float’s: l (1 e 20 + -1 e 20) + 3. 14 --> 3. 14 l 1 e 20 + (-1 e 20 + 3. 14) --> ? ? – 6– CSCESource: 212 Hxkcd. com/571 Spring 2018

Carnegie Mellon Computer Arithmetic Does not generate random values n Arithmetic operations have important mathematical properties Cannot assume all “usual” mathematical properties n n Due to finiteness of representations Integer operations satisfy “ring” properties l Commutativity, associativity, distributivity n Floating point operations satisfy “ordering” properties l Monotonicity, values of signs Observation n n – 7– Need to understand which abstractions apply in which contexts Important issues for compiler writers and serious application programmers CSCE 212 H Spring 2018

Carnegie Mellon Great Reality #2: You’ve Got to Know Assembly Chances are, you’ll never write programs in assembly n Compilers are much better & more patient than you are But: Understanding assembly is key to machine-level execution model n Behavior of programs in presence of bugs l High-level language models break down n Tuning program performance l Understand optimizations done / not done by the compiler l Understanding sources of program inefficiency n Implementing system software l Compiler has machine code as target l Operating systems must manage process state n – 8– Creating / fighting malware l x 86 assembly is the language of choice! CSCE 212 H Spring 2018

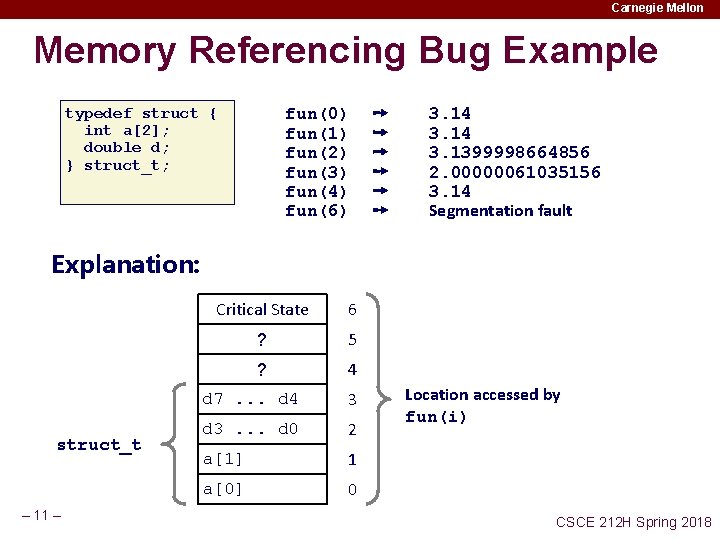
Carnegie Mellon Great Reality #3: Memory Matters Random Access Memory Is an Unphysical Abstraction Memory is not unbounded n n It must be allocated and managed Many applications are memory dominated Memory referencing bugs especially pernicious n Effects are distant in both time and space Memory performance is not uniform n n – 9– Cache and virtual memory effects can greatly affect program performance Adapting program to characteristics of memory system can lead to major speed improvements CSCE 212 H Spring 2018

Carnegie Mellon Memory Referencing Bug Example typedef struct { int a[2]; double d; } struct_t; double fun(int i) { volatile struct_t s; s. d = 3. 14; s. a[i] = 1073741824; /* Possibly out of bounds */ return s. d; } fun(0) fun(1) fun(2) fun(3) fun(4) fun(6) n – 10 – ➙ ➙ ➙ 3. 14 3. 1399998664856 2. 00000061035156 3. 14 Segmentation fault Result is system specific CSCE 212 H Spring 2018

Carnegie Mellon Memory Referencing Bug Example fun(0) fun(1) fun(2) fun(3) fun(4) fun(6) typedef struct { int a[2]; double d; } struct_t; ➙ ➙ ➙ 3. 14 3. 1399998664856 2. 00000061035156 3. 14 Segmentation fault Explanation: struct_t – 11 – Critical State 6 ? 5 ? 4 d 7. . . d 4 3 d 3. . . d 0 2 a[1] 1 a[0] 0 Location accessed by fun(i) CSCE 212 H Spring 2018

Carnegie Mellon Memory Referencing Errors C and C++ do not provide any memory protection n Out of bounds array references n Invalid pointer values Abuses of malloc/free n Can lead to nasty bugs n n Whether or not bug has any effect depends on system and compiler Action at a distance l Corrupted object logically unrelated to one being accessed l Effect of bug may be first observed long after it is generated How can I deal with this? n n n – 12 – Program in Java, Ruby, Python, ML, … Understand what possible interactions may occur Use or develop tools to detect referencing errors (e. g. Valgrind) CSCE 212 H Spring 2018

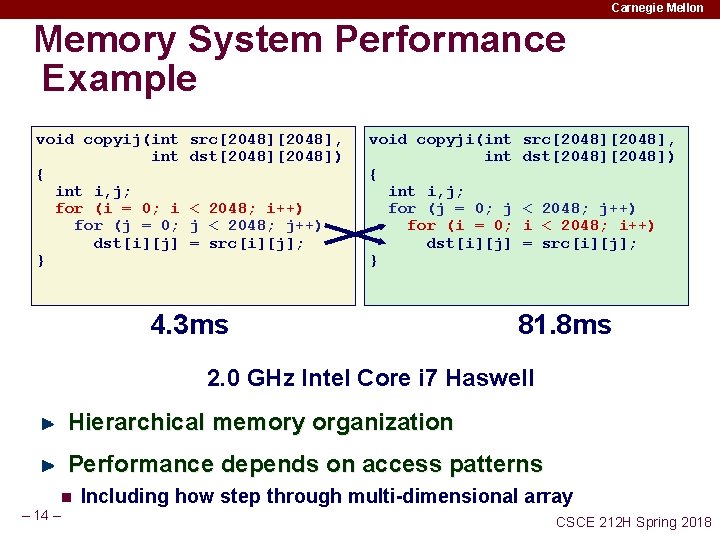
Carnegie Mellon Great Reality #4: There’s more to performance than asymptotic complexity Constant factors matter too! And even exact op count does not predict performance n n Easily see 10: 1 performance range depending on how code written Must optimize at multiple levels: algorithm, data representations, procedures, and loops Must understand system to optimize performance n n n – 13 – How programs compiled and executed How to measure program performance and identify bottlenecks How to improve performance without destroying code modularity and generality CSCE 212 H Spring 2018

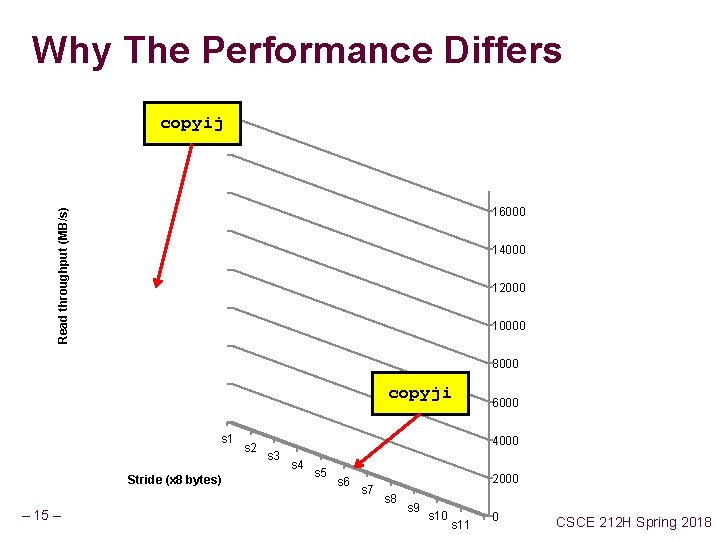
Carnegie Mellon Memory System Performance Example void copyij(int { int i, j; for (i = 0; i for (j = 0; dst[i][j] } src[2048], dst[2048]) < 2048; i++) j < 2048; j++) = src[i][j]; void copyji(int { int i, j; for (j = 0; j for (i = 0; dst[i][j] } 4. 3 ms src[2048], dst[2048]) < 2048; j++) i < 2048; i++) = src[i][j]; 81. 8 ms 2. 0 GHz Intel Core i 7 Haswell Hierarchical memory organization Performance depends on access patterns n – 14 – Including how step through multi-dimensional array CSCE 212 H Spring 2018

Why The Performance Differs copyij Read throughput (MB/s) 16000 14000 12000 10000 8000 copyji s 1 Stride (x 8 bytes) – 15 – s 2 6000 4000 s 3 s 4 s 5 s 6 s 7 2000 s 8 s 9 s 10 s 11 0 CSCE 212 H Spring 2018

Carnegie Mellon Great Reality #5: Computers do more than execute programs They need to get data in and out n I/O system critical to program reliability and performance They communicate with each other over networks n Many system-level issues arise in presence of network l Concurrent operations by autonomous processes l Coping with unreliable media l Cross platform compatibility l Complex performance issues – 16 – CSCE 212 H Spring 2018

Bits and Bytes n n Why bits? Representing information as bits l Binary/Hexadecimal l Byte representations » numbers » characters and strings » Instructions n Bit-level manipulations l Boolean algebra l Expressing in C How much C do we Know? – 17 – CSCE 212 H Spring 2018

Byte-Oriented Memory Organization Programs Refer to Virtual Addresses n n n Conceptually very large array of bytes Actually implemented with hierarchy of different memory types l SRAM, DRAM, disk l Only allocate for regions actually used by program In Unix and Windows NT, address space private to particular “process” l Program being executed l Program can clobber its own data, but not that of others Compiler + Run-Time System Control Allocation n – 18 – Where different program objects should be stored Multiple mechanisms: static, stack, and heap In any case, allocation within single virtual address space CSCE 212 H Spring 2018

Words Machine Has “Word Size” n Nominal size of integer-valued data l Including addresses n Most current machines are 32 bits (4 bytes) l Limits addresses to 4 GB l Becoming too small for memory-intensive applications n High-end systems are 64 bits (8 bytes) l Potentially address 1. 8 X 1019 bytes n Machines support multiple data formats l Fractions or multiples of word size l Always integral number of bytes Word-Oriented Memory Organization – 19 – CSCE 212 H Spring 2018

Byte Order Big Endian n Least significant byte has highest address Little Endian n Least significant byte has lowest address Example n n – 20 – Variable x has 4 -byte representation 0 x 01234567 Address given by &x is 0 x 100 CSCE 212 H Spring 2018

Reading Byte-Reversed Listings Disassembly n Text representation of binary machine code n Generated by program that reads machine code Example Fragment Address Instruction Code. Assembly Rendition 8048365: 5 b pop 8048366: 81 c 3 ab 12 00 00 add $0 x 12 ab, %ebx 804836 c: 83 bb 28 00 00 cmpl Deciphering Numbers $0 x 0, 0 x 28(%ebx) n. Value: n. Pad – 21 – 0 x 12 ab to 4 bytes: n. Split %ebx 0 x 000012 ab into bytes: 00 00 12 ab n. Reverse: ab 12 00 00 CSCE 212 H Spring 2018

Code to Print Byte Representation of Data typedef unsigned char *pointer; void show_bytes(pointer start, int len) { int i; for (i = 0; i < len; i++) printf("0 x%pt 0 x%. 2 xn", start+i, start[i]); printf("n"); } – 22 – Printf directives: %p: Print pointer %x: Print Hexadecimal CSCE 212 H Spring 2018

show_bytes Execution Example int a = 15213; printf("int a = 15213; n"); show_bytes((pointer) &a, sizeof(int)); Result (Linux): int a = 15213; 0 x 11 ffffcb 8 0 x 6 d 0 x 11 ffffcb 9 0 x 3 b 0 x 11 ffffcba 0 x 00 0 x 11 ffffcbb 0 x 00 – 23 – CSCE 212 H Spring 2018

Strings in C n Represented by array of characters n Each character encoded in ASCII format l Standard 7 -bit encoding of character set l Other encodings exist, but uncommon l Character “ 0” has code 0 x 30 n » Digit i has code 0 x 30+i String should be null-terminated l Final character = 0 Compatibility n Byte ordering not an issue l Data are single byte quantities n – 24 – Text files generally platform independent l Except for different conventions of line termination character(s)! CSCE 212 H Spring 2018

Machine-Level Code Representation Encode Program as Sequence of Instructions n Each simple operation l Arithmetic operation l Read or write memory l Conditional branch n Instructions encoded as bytes l Alpha’s, Sun’s, Mac’s use 4 byte instructions » Reduced Instruction Set Computer (RISC) l PC’s use variable length instructions n » Complex Instruction Set Computer (CISC) Different instruction types and encodings for different machines l Most code not binary compatible Programs are Byte Sequences Too! – 25 – CSCE 212 H Spring 2018

Relations Between Operations De. Morgan’s Laws n Express & in terms of |, and vice-versa l A & B = ~(~A | ~B) » A and B are true if and only if neither A nor B is false l A | B = ~(~A & ~B) » A or B are true if and only if A and B are not both false Exclusive-Or using Inclusive Or l A ^ B = (~A & B) | (A & ~B) » Exactly one of A and B is true l A ^ B = (A | B) & ~(A & B) » Either A is true, or B is true, but not both – 26 – CSCE 212 H Spring 2018

General Boolean Algebras Operate on Bit Vectors n Operations are applied bitwise 01101001 & 0101 01000001 01101001 | 0101 01111101 01101001 ^ 0101 00111100 ~ 0101 1010 All of the Properties of Boolean Algebra Apply – 27 – CSCE 212 H Spring 2018

Representing & Manipulating Sets Representation n n Width w bit vector represents subsets of {0, …, w– 1} aj = 1 if j A 01101001 { 0, 3, 5, 6 } 76543210 0101 76543210 { 0, 2, 4, 6 } Operations n n – 28 – & Intersection | Union ^ Symmetric difference ~ Complement 01000001 01111101 00111100 1010 { 0, 6 } { 0, 2, 3, 4, 5, 6 } { 2, 3, 4, 5 } { 1, 3, 5, 7 } CSCE 212 H Spring 2018

Bit-Level Operations in C Operations &, |, ~, ^ Available in C n Apply to any “integral” data type n View arguments as bit vectors Arguments applied bit-wise n l long, int, short, char Examples (Char data type) n ~0 x 41 --> 0 x. BE ~0 x 00 --> 0 x. FF ~010000012 n ~00002 --> n --> 101111102 11112 0 x 69 & 0 x 55 --> 0 x 41 0 x 69 | 0 x 55 --> 0 x 7 D 011010012 & 01012 --> 010000012 n 011010012 | 01012 --> 011111012 – 29 – CSCE 212 H Spring 2018

Contrast: Logic Operations in C Contrast to Logical Operators n &&, ||, ! l l View 0 as “False” Anything nonzero as “True” Always return 0 or 1 Early termination Examples (char data type) n n n – 30 – !0 x 41 --> !0 x 00 --> !!0 x 41 --> 0 x 69 && 0 x 55 0 x 69 || 0 x 55 p && *p 0 x 00 0 x 01 --> 0 x 01 (avoids null pointer access) CSCE 212 H Spring 2018

Shift Operations Left Shift: n x << y Shift bit-vector x left y positions l Throw away extra bits on left l Fill with 0’s on right Right Shift: n x >> y Shift bit-vector x right y positions l Throw away extra bits on right n Logical shift l Fill with 0’s on left n Arithmetic shift l Replicate most significant bit on right l Useful with two’s complement integer representation – 31 – CSCE 212 H Spring 2018

XOR n n Bitwise Xor is form of addition With extra property that every value is its own additive inverse A^A=0 void funny(int *x, int *y) { *x = *x ^ *y; /* #1 */ *y = *x ^ *y; /* #2 */ *x = *x ^ *y; /* #3 */ } – 32 – CSCE 212 H Spring 2018

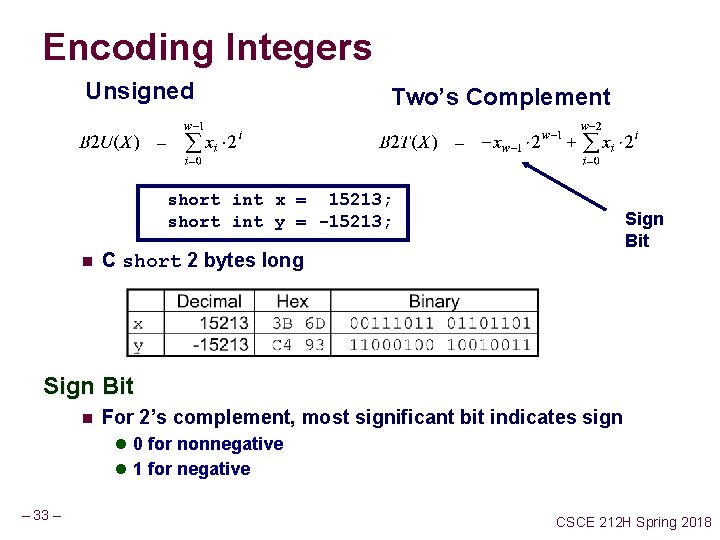
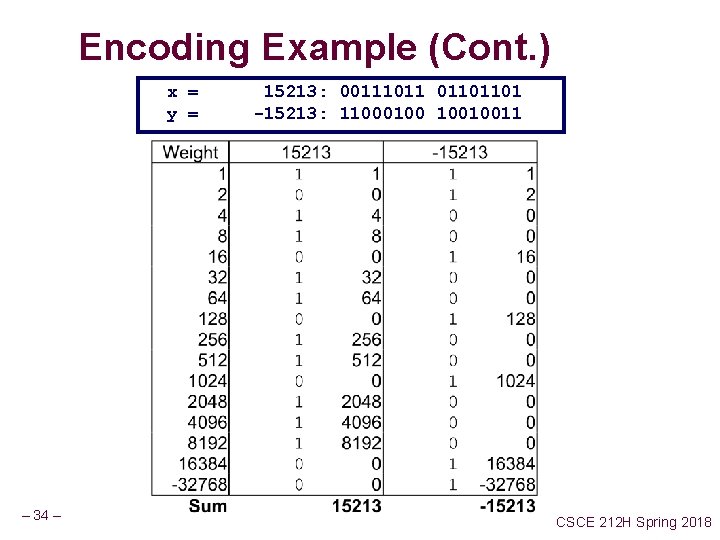
Encoding Integers Unsigned Two’s Complement short int x = 15213; short int y = -15213; n Sign Bit C short 2 bytes long Sign Bit n For 2’s complement, most significant bit indicates sign l 0 for nonnegative l 1 for negative – 33 – CSCE 212 H Spring 2018

Encoding Example (Cont. ) x = y = – 34 – 15213: 00111011 01101101 -15213: 11000100 10010011 CSCE 212 H Spring 2018

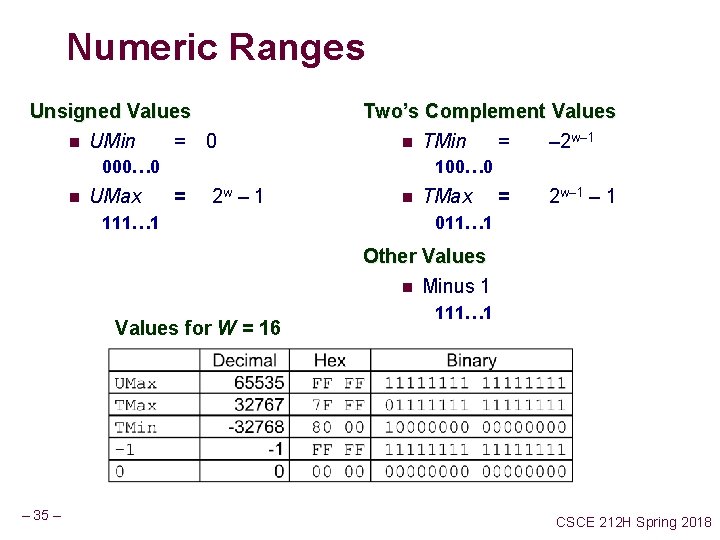
Numeric Ranges Unsigned Values n UMin = 0 Two’s Complement Values n TMin = – 2 w– 1 000… 0 n UMax 100… 0 = 2 w – 1 111… 1 n TMax = 2 w– 1 011… 1 Other Values n Minus 1 Values for W = 16 – 35 – 111… 1 CSCE 212 H Spring 2018

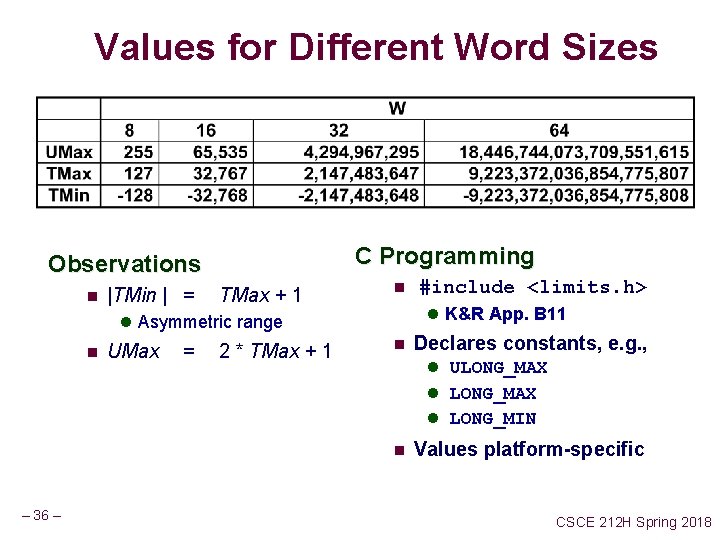
Values for Different Word Sizes C Programming Observations n |TMin | = TMax + 1 n l K&R App. B 11 l Asymmetric range n UMax = 2 * TMax + 1 #include <limits. h> n Declares constants, e. g. , l ULONG_MAX l LONG_MIN n – 36 – Values platform-specific CSCE 212 H Spring 2018

Casting Signed to Unsigned C Allows Conversions from Signed to Unsigned short int x = 15213; unsigned short int ux = (unsigned short) x; short int y = -15213; unsigned short int uy = (unsigned short) y; Resulting Value n n No change in bit representation Nonnegative values unchanged l ux = 15213 n Negative values change into (large) positive values l uy = 50323 – 37 – CSCE 212 H Spring 2018

Relation Between Signed & Unsigned n – 38 – uy = y + 2 * 32768 = y + 65536 CSCE 212 H Spring 2018

Signed vs. Unsigned in C Constants n By default are considered to be signed integers n Unsigned if have “U” as suffix 0 U, 4294967259 U Casting n Explicit casting between signed & unsigned same as U 2 T and T 2 U int tx, ty; unsigned ux, uy; tx = (int) ux; uy = (unsigned) ty; n Implicit casting also occurs via assignments and procedure calls tx = ux; uy = ty; – 39 – CSCE 212 H Spring 2018

Casting Surprises Expression Evaluation n If mix unsigned and signed in single expression, signed values implicitly cast to unsigned n Including comparison operations <, >, ==, <=, >= n Examples Constant 1 for W = 32 0 0 U == -1 0 U 2147483647 – 40 – Constant 2 unsigned 0 U <0 signed > 0 U unsigned -2147483648 Relation Evaluation > 2147483647 U -2147483648 < -2147483648 -1 -2 > -2 signed (unsigned) -1 -2 > unsigned -1 -2 2147483647 2147483648 U < 2147483648 U 2147483647 (int)2147483648 U> signed unsigned CSCE 212 H Spring 2018

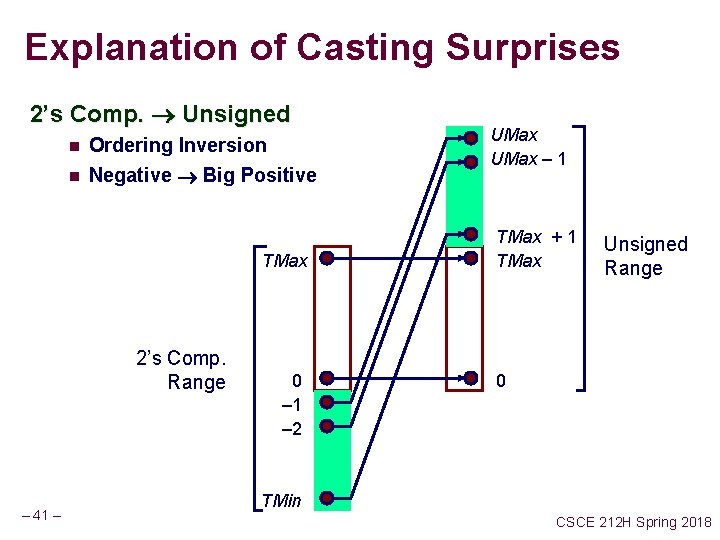
Explanation of Casting Surprises 2’s Comp. Unsigned n Ordering Inversion n Negative Big Positive TMax 2’s Comp. Range – 41 – 0 – 1 – 2 UMax – 1 TMax + 1 TMax Unsigned Range 0 TMin CSCE 212 H Spring 2018

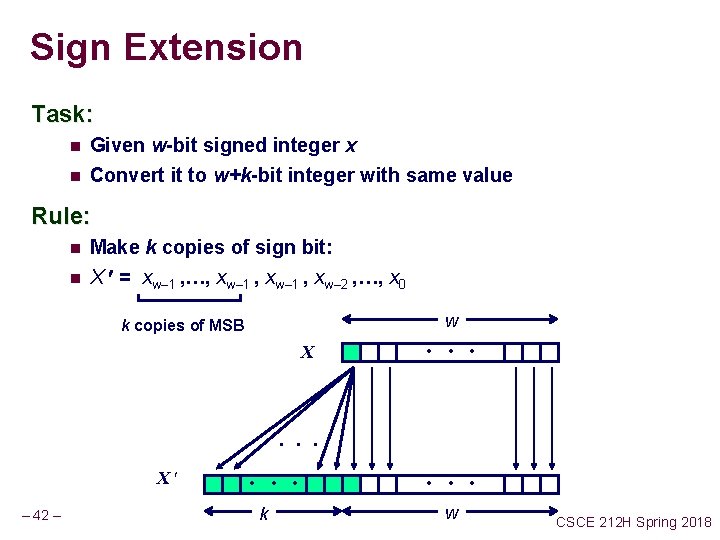
Sign Extension Task: n Given w-bit signed integer x n Convert it to w+k-bit integer with same value Rule: n n Make k copies of sign bit: X = xw– 1 , …, xw– 1 , xw– 2 , …, x 0 w k copies of MSB X • • • X – 42 – • • • k • • • w CSCE 212 H Spring 2018

Sign Extension Example short int x = 15213; int ix = (int) x; short int y = -15213; int iy = (int) y; Decimal Hex 3 B 15213 00 00 3 B C 4 -15213 FF FF C 4 x ix y iy n n – 43 – 6 D 6 D 93 93 Binary 00111011 00000000 00111011 11000100 11111111 11000100 01101101 10010011 Converting from smaller to larger integer data type C automatically performs sign extension CSCE 212 H Spring 2018

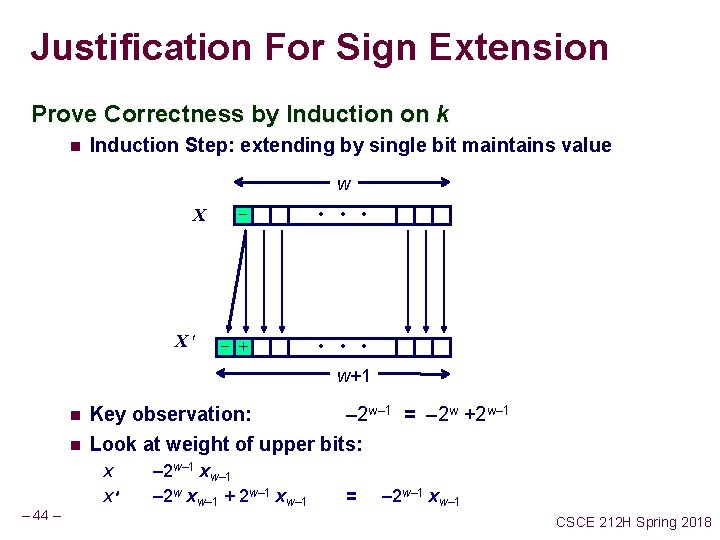
Justification For Sign Extension Prove Correctness by Induction on k n Induction Step: extending by single bit maintains value w X X - • • • - + • • • w+1 n n Key observation: – 2 w– 1 = – 2 w +2 w– 1 Look at weight of upper bits: X X – 44 – – 2 w– 1 xw– 1 – 2 w xw– 1 + 2 w– 1 xw– 1 = – 2 w– 1 xw– 1 CSCE 212 H Spring 2018

Why Should I Use Unsigned? Don’t Use Just Because Number Nonzero n C compilers on some machines generate less efficient code unsigned i; for (i = 1; i < cnt; i++) a[i] += a[i-1]; n Easy to make mistakes for (i = cnt-2; i >= 0; i--) a[i] += a[i+1]; Do Use When Performing Modular Arithmetic n n Multiprecision arithmetic Other esoteric stuff Do Use When Need Extra Bit’s Worth of Range n – 45 – Working right up to limit of word size CSCE 212 H Spring 2018

Negating with Complement & Increment Claim: Following Holds for 2’s Complement ~x + 1 == -x Complement n Observation: ~x + x == 1111… 112 == -1 x 1001 110 1 + ~x 0110 001 0 -1 111 1 Increment n n ~x + (-x + 1) ~x + 1 == == -1 + (-x + 1) -x Warning: Be cautious treating int’s as integers – 46 – n OK here CSCE 212 H Spring 2018

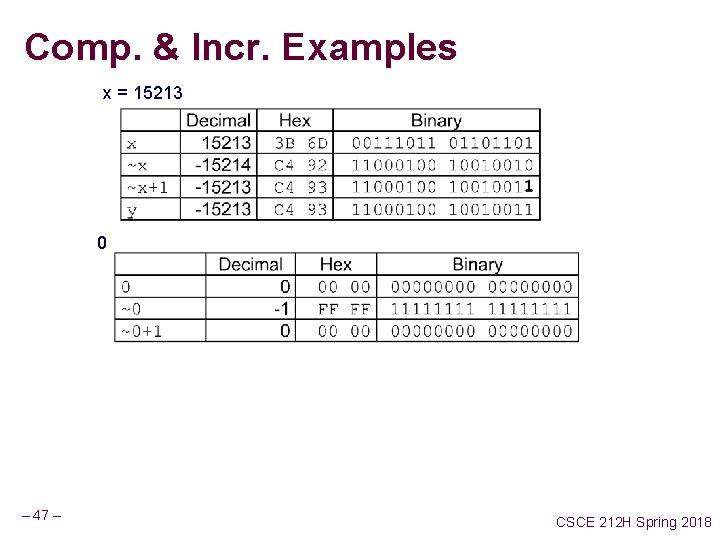
Comp. & Incr. Examples x = 15213 0 – 47 – CSCE 212 H Spring 2018

Unsigned Addition u • • • v • • • u+v • • • UAddw(u , v) • • • Operands: w bits + True Sum: w+1 bits Discard Carry: w bits Standard Addition Function n Ignores carry output Implements Modular Arithmetic s = – 48 – UAddw(u , v) = u + v mod 2 w CSCE 212 H Spring 2018

Mathematical Properties Modular Addition Forms an Abelian Group n Closed under addition 0 UAddw(u , v) 2 w – 1 n Commutative UAddw(u , v) = UAddw(v , u) n Associative UAddw(t, UAddw(u , v)) = UAddw(t, u ), v) n 0 is additive identity UAddw(u , 0) = u n Every element has additive inverse l Let UCompw (u ) = 2 w – u UAddw(u , UCompw (u )) = 0 – 49 – CSCE 212 H Spring 2018

Two’s Complement Addition u • • • v • • • u+v • • • TAddw(u , v) • • • Operands: w bits + True Sum: w+1 bits Discard Carry: w bits TAdd and UAdd have Identical Bit-Level Behavior n n – 50 – Signed vs. unsigned addition in C: int s, t, u, v; s = (int) ((unsigned) u + (unsigned) v); t = u + v Will give s == t CSCE 212 H Spring 2018

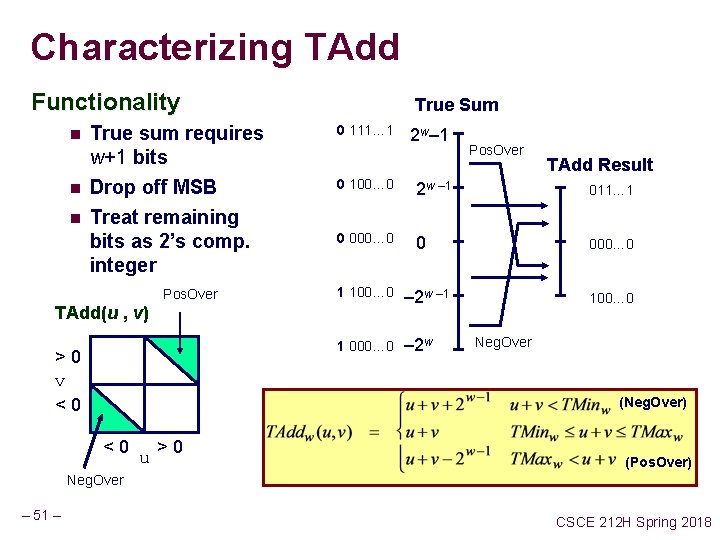
Characterizing TAdd Functionality n n n True sum requires w+1 bits Drop off MSB Treat remaining bits as 2’s comp. integer Pos. Over True Sum 0 111… 1 Pos. Over TAdd Result 0 100… 0 2 w – 1 011… 1 0 000… 0 1 100… 0 – 2 w – 1 1 000… 0 – 2 w TAdd(u , v) >0 v <0 2 w– 1 100… 0 Neg. Over (Neg. Over) <0 u >0 (Pos. Over) Neg. Over – 51 – CSCE 212 H Spring 2018

Detecting 2’s Comp. Overflow Task 2 w– 1 n Given s = TAddw(u , v) n Determine if s = Addw(u , v) Example int s, u, v; s = u + v; n Pos. Over 2 w – 1 0 Claim n Overflow iff either: Neg. Over u, v < 0, s 0 (Neg. Over) u, v 0, s < 0 (Pos. Over) ovf = (u<0 == v<0) && (u<0 != s<0); – 52 – CSCE 212 H Spring 2018

Mathematical Properties of TAdd Isomorphic Algebra to UAdd n TAddw(u , v) = U 2 T(UAddw(T 2 U(u ), T 2 U(v))) l Since both have identical bit patterns Two’s Complement Under TAdd Forms a Group n n Closed, Commutative, Associative, 0 is additive identity Every element has additive inverse Let TCompw (u ) = U 2 T(UCompw(T 2 U(u )) TAddw(u , TCompw (u )) = 0 – 53 – CSCE 212 H Spring 2018

Unsigned vs. Signed Multiplication Unsigned Multiplication unsigned ux = (unsigned) x; unsigned uy = (unsigned) y; unsigned up = ux * uy n n Truncates product to w-bit number up = UMultw(ux, uy) Modular arithmetic: up = ux uy mod 2 w Two’s Complement Multiplication int x, y; int p = x * y; n n – 54 – Compute exact product of two w-bit numbers x, y Truncate result to w-bit number p = TMultw(x, y) CSCE 212 H Spring 2018

Unsigned vs. Signed Multiplication Unsigned Multiplication unsigned ux = (unsigned) x; unsigned uy = (unsigned) y; unsigned up = ux * uy Two’s Complement Multiplication int x, y; int p = x * y; Relation n n – 55 – Signed multiplication gives same bit-level result as unsigned up == (unsigned) p CSCE 212 H Spring 2018

Properties of Two’s Comp. Arithmetic Isomorphic Algebras n Unsigned multiplication and addition l Truncating to w bits n Two’s complement multiplication and addition l Truncating to w bits Both Form Rings n Isomorphic to ring of integers mod 2 w Comparison to Integer Arithmetic n n Both are rings Integers obey ordering properties, e. g. , u>0 u > 0, v > 0 n – 56 – u+v>v u·v>0 These properties are not obeyed by two’s comp. arithmetic TMax + 1 == 15213 * 30426 TMin == -10030 (16 -bit words) CSCE 212 H Spring 2018

C Puzzles n n n Taken from old exams Assume machine with 32 bit word size, two’s complement integers For each of the following C expressions, either: l Argue that is true for all argument values l Give example where not true ((x*2) < 0) • x & 7 == 7 (x<<30) < 0 • x < 0 Initialization • ux >= 0 int x = foo(); • ux > -1 int y = bar(); • x > y unsigned ux = x; • x * x >= 0 unsigned uy = y; • x > 0 && y > 0 – 57 – -x < -y x + y > 0 • x >= 0 -x <= 0 • x <= 0 -x >= CSCE 0 212 H Spring 2018

C Puzzle Answers n n Assume machine with 32 bit word size, two’s comp. integers TMin makes a good counterexample in many cases TMin x < 0 q ux >= 0 q x & 7 == 7 q ux > -1 q x > y q x * x >= 0 q x > 0 && y > 0 q x >= 0 -x <= 0 True: –TMax < 0 q x <= 0 -x >= 0 False: TMin – 58 – ((x*2) < 0) False: q True: (x<<30) < 0 False: -x < -y False: 0 = UMin True: x 1 = 1 0 False: -1, TMin 30426 x + y > 0 False: TMax, TMax CSCE 212 H Spring 2018