CSCE 211 Digital Design Lecture 3 Boolean algebra

CSCE 211 Digital Design Lecture 3 Boolean algebra Topics n Error Correcting Codes n Boolean algebra Combinational circuits Algebraic analysis, Truth tables, Logic Diagrams Sums-of-Products and Products-of-Sums n n n August 31, 2015

Overview Last Time: n n BCD, excess-3 Ripple carry Adder Two’s complement IEEE 754 floats New: n n n Some from Lecture 02: floats again; two’s complement overflow Boolean Algebra Basic Gates: symbols and truth tables l for : AND, OR, NOT, NOR, NAND, XOR, n n n Half Adder: table and circuit Full Adder: Table and logic diagram from 2 Half-adders + ? ? ? Gray Code, Error Correcting Codes Example Error Correcting Codes Combinational circuits l Algebraic analysis, Truth tables, Logic Diagrams n – 2– Sums-of-Products and Products-of-Sums CSCE 211 H Fall 2015

Pop. Quiz 1. Convert 11011. 010012 to hex 1. Convert 37. 0310 to Octal 2. Give the representation of 37. 0310 as a IEEE 754 float a. b. d. What is the Actual Exponent? What is the exponent field? e. What is the fraction field? c. 2. Octal to binary is like hex to binary except groups of 3 since 23 = 8 Convert 37. 0310 to binary – 3– What is the sign bit? Write in “binary” scientific notation(normalized) CSCE 211 H Fall 2015

Boolean Algebra George Boole (1854) invented a two valued algebra To “give expression … to the fundamental laws of reasoning in the symbolic language of a Calculus. ” 1938 Claude Shannon at Bell Labs noted that this Boolean logic could be used to describe switching circuits. (Switching Algebra) In Shannon’s view a relay has two positions open and closed representing 1 and 0. Collections of relays satisfied the properties of Boolean algebra. – 4– CSCE 211 H Fall 2015

Basic Gates – 5– CSCE 211 H Fall 2015

Describing Circuits: Ex. Half-adder Boolean Expression Block diagram symbol Logic Diagram Truth Table – 6– CSCE 211 H Fall 2015

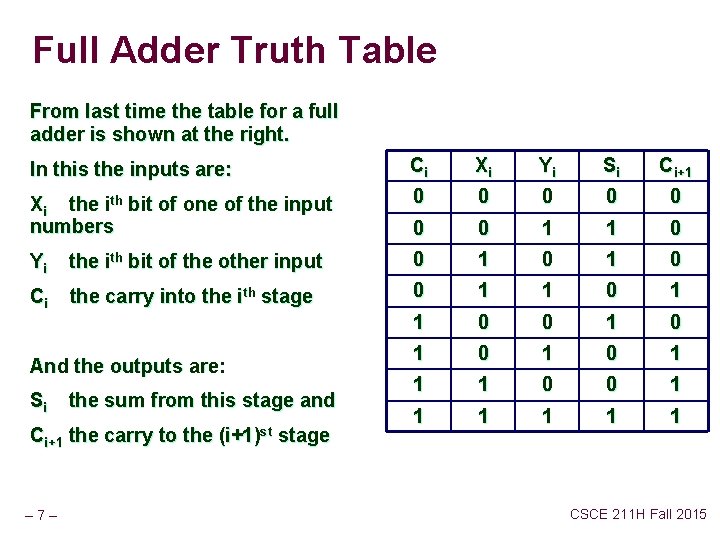
Full Adder Truth Table From last time the table for a full adder is shown at the right. In this the inputs are: Ci Xi Yi Si Ci+1 Xi the ith bit of one of the input numbers 0 0 0 0 1 1 0 Yi the ith bit of the other input 0 1 0 Ci the carry into the ith stage 0 1 1 0 0 1 0 1 1 1 0 0 1 1 1 And the outputs are: Si the sum from this stage and Ci+1 the carry to the (i+1)st stage – 7– CSCE 211 H Fall 2015

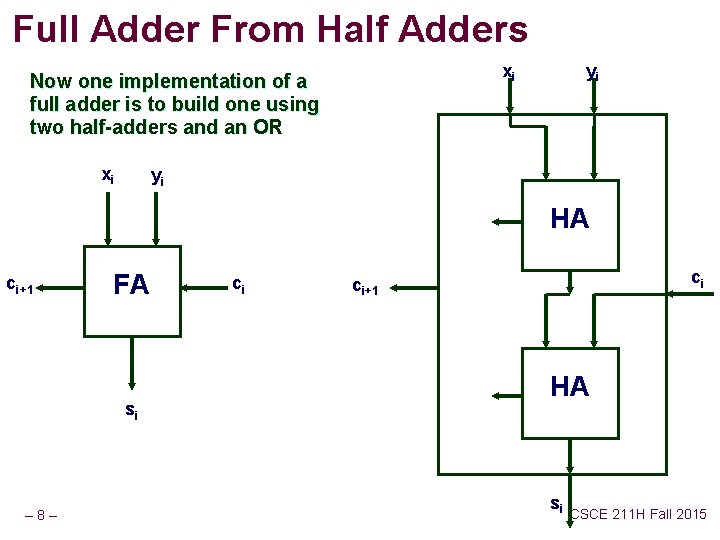
Full Adder From Half Adders xi Now one implementation of a full adder is to build one using two half-adders and an OR xi yi yi HA ci+1 FA si – 8– ci ci ci+1 HA si CSCE 211 H Fall 2015

Error Correcting codes Revisited For an n-bit code, consider the hypercube of dimension n Choose some subset of the nodes as code words. Suppose the distance between any two code words is at least 3. Now consider transmission errors. Then if there is an error in transmitting just one bit then the distance from the received word to one code word is one, distances to other code words are at least two. Single error correcting, double error detecting. Such codes are called Hamming codes after their inventor Richard Hamming. – 9– CSCE 211 H Fall 2015

Boolean Algebra Axioms The axioms of a mathematical system are a minimal set of properties that are assumed to be true. Axioms of Boolean Algebra 1. X = 0 if X != 1 1’. X=1 if X!=0 2. If X = 0, then X’ = 1 3. 0. 0 = 0 2’. if X=1 then X’=0 4. 1. 1 = 1 5. 0. 1 = 1. 0 = 0 4’. 0 + 0 = 0 3’. 1 + 1 = 1 5’. 1 + 0 = 0 + 1 = 1 Axioms 1 -5 and 1’-5’ completely define what it means to be a Boolean algebra. – 10 – CSCE 211 H Fall 2015

Boolean Algebra Theorems We can prove a new theorem: l By directly applying axioms and other already proved theorems, or l By perfect induction, i. e. considering all possible cases n – 11 – Truth tables CSCE 211 H Fall 2015

Consider a Proof from the axioms Prove Theorem “T 5: X + X’ = 1” from the axioms Proof: First suppose that X=1. Then by Axiom 2’ (if X=1 then X’=0) we have X’=0 and thus X + X’ = 1 + 0 and then by Axiom 5’ (1+0 = 1) and so X + X’ = 1. Now if X != 1 then by Axiom 1 (X = 0 if X != 1) and we have X = 0. Then by Axiom 2 (If X = 0, then X’ = 1) we have X’=1 and so X + X’ = 0 + 1 and again by axiom 5’ (0 + 1 = 1) we have X + X’ = 1 – 12 – CSCE 211 H Fall 2015

More Theorems N. B. T 8¢, T 10, T 11 – 13 – CSCE 211 H Fall 2015

Consider a Truth Table Proof Prove Theorem “T 8’: (X+Y). (X+Z) = X + Y. Z” using a truth table X Y Z 0 0 0 1 1 1 0 0 1 1 1 X+Y X+Z (X+Y). (X+Z) X Y. Z X + Y. Z Then since the “(X+Y). (X+Z)” column and the “X + Y. Z” column are …. for all possible values of X, Y and Z this truth table proves … – 14 – CSCE 211 H Fall 2015

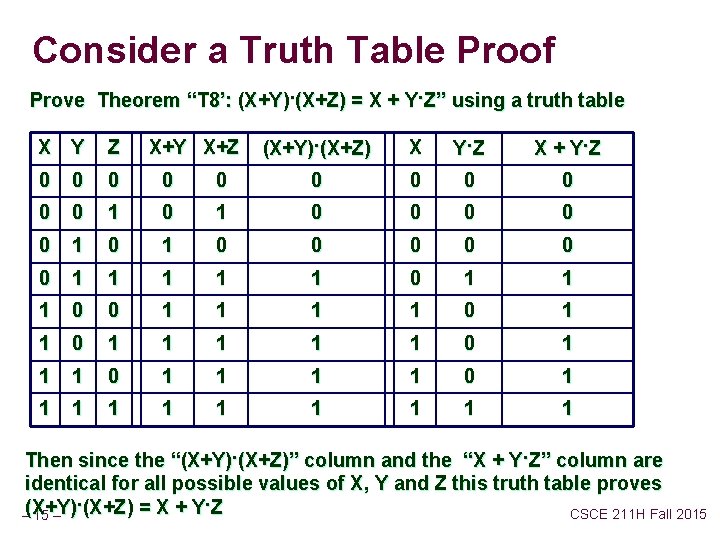
Consider a Truth Table Proof Prove Theorem “T 8’: (X+Y). (X+Z) = X + Y. Z” using a truth table (X+Y). (X+Z) X Y. Z X + Y. Z 0 0 0 1 0 0 0 0 0 1 1 1 0 0 1 1 0 1 1 1 1 1 X Y Z X+Y X+Z 0 0 0 1 0 Then since the “(X+Y). (X+Z)” column and the “X + Y. Z” column are identical for all possible values of X, Y and Z this truth table proves. (X+Z) = X + Y. Z CSCE 211 H Fall 2015 –(X+Y) 15 –

Duals Given a boolean equation then we can take its dual by n Replacing each 1 with 0, n replacing each 0 with a 1, n replacing each ‘+’ (OR) with ‘. ’ (AND), and n replacing each ‘. ’ (AND) with a ‘+’ (OR) Example: The dual of X. Y + X. Z = X. (Y+Z) is … – 16 – CSCE 211 H Fall 2015

Principle of Duality Given a boolean equation E that is a theorem if we take the dual then the resulting equation is also a theorem. Why? n Each axiom (A 1 -A 5) has a dual (A 1¢-A 5¢) Example: X + (Y + Z) = (X + Y) + Z X × (Y × Z) = (X × Y) × Z (this is theorem T 7) (taking the dual yields T 7’) Example 2: X + X’ = 1 (Axiom A 5) X × X’ = 0 (taking the dual yields Axiom A 5’) – 17 – CSCE 211 H Fall 2015

Principle of Duality 2 Now consider the following argument using duals X+X×Y=X (this is theorem T 9) X×X+Y=X (by taking the dual ? ? ? ) X+Y=X (But then X × X = X by T 3¢) Counterexample? This is not true! (consider X=0, Y=1) Where did we go wrong? X + (X × Y) = X X × (X + Y) = X (X × X) + (X × Y) = X X + (X × Y) = X – 18 – (T 9 fully parenthesized) (dual) (using T 8 to rewrite left side) (the using T 3¢) CSCE 211 H Fall 2015

N-variable Theorems Prove using finite induction Most important: De. Morgan theorems – 19 – CSCE 211 H Fall 2015

Combinational Circuit Analysis A combinational circuit is one whose outputs are a function of its inputs and only its inputs. These circuits can be analyzed using: 1. Truth tables 2. Algebraic equations 3. Logic diagrams – 20 – CSCE 211 H Fall 2015

Boolean Algebra Proofs Axioms n Statements (boolean equations) that are assumed to be true that form the basis of a mathematical system. Theorems n Statements that can be “proved” from the axioms and earlier theorems. Lemmas, Corollaries, Postulates Proof by truth-table n For a “possible theorem” with a small number of variables, we can exhaustively consider all possible cases. Algebraic Proofs n Apply axioms and previously proven theorems to rewrite a “possible theorem” until it is reduced to an equation known to be true. Induction n – 21 – n Basis case: P(1) Inductive hypothesis: Assuming P(n) show P(n+1) CSCE 211 H Fall 2015

Proof by truth-table Prove Demorgan’s Law: (X+Y)' = X '. Y ' X Y 0 0 0 1 1 (X+Y)' X' Y' X'. Y' Note the table considers all possible cases and in each case the value in the column for (X+Y)' is equal to the value in the column for X'. Y' So, (X+Y) ' = X'. Y' – 22 – CSCE 211 H Fall 2015

Algebraic Simplification Simplify F = A. B. C’. D + D. C. A + B. C. D + A’. B’. C. D – 23 – CSCE 211 H Fall 2015

Proof by Induction Thereom 13 (X 1. X 2. X 3 …. Xn)’ = X 1’ + X 2’ + X 3’ … + Xn’ Proof: Basis Step n = 2, (X 1. X 2)’ = X 1’ + X 2’ was proven using a truth-table. Now suppose as inductive hypothesis that (X 1. X 2. X 3 …. Xn)’ = X 1’ + X 2’ + X 3’ … + Xn’ Then consider n n – 24 – (X 1. X 2. …. Xn+1)’ = ((X 1. X 2. X 3 …. Xn ). Xn+1)’ by associativity = (X 1. X 2. X 3 …. Xn )’ + Xn+1’ by the basis step = (X 1’ + X 2’ + X 3’ … + Xn’) + Xn+1’ by the inductive hypothesis CSCE 211 H Fall 2015

Universal Sets of Gates A set of Gates(operators), S, is universal if every boolean function can be expressed using gates only from S. Examples l {AND, OR, NOT} is a universal set l {NAND} is a universal set – 25 – CSCE 211 H Fall 2015

Universal Sets of Gates (cont. ) Examples l {AND, OR} is not l {NOR}? l {XOR}? HW – 26 – CSCE 211 H Fall 2015

Combinational Circuit Analysis A combinational circuit is one whose outputs are a function of its inputs and only its inputs. These circuits can be analyzed using: 1. Truth tables 2. Algebraic equations 3. Logic diagrams – timing considerations; graphical – 27 – CSCE 211 H Fall 2015

Switching Algebra Terminology Literal – a variable or the complement of a variable Product term – a single literal or the AND of several literals Sum term – a single literal or the OR of several literals Sums-of-products Product-of-sums Normal term – a product (sum) term in which no variable appears twice Minterm – a normal product term with n literals Maxterm – a normal sum term with n literals – 28 – CSCE 211 H Fall 2015

Timing Analysis We will do some extensive timing analysis in the labs but for right now we will assume the delay for and an AND-gate and an OR-gate is “d” When we fabricate circuits there a couple special circumstances: 1. Inverters (Not gates) cost nothing 2. Circuits are usually fabricated from “NANDs” – 29 – CSCE 211 H Fall 2015

Circuit Simplification Why would we want to simplify circuits? n To minimize time delays n To minimize costs To minimize area n – 30 – CSCE 211 H Fall 2015

Sums-of-Products What is the delay of sums-of-products circuit? – 31 – CSCE 211 H Fall 2015

Circuit Simplification Minterms – a product term in which every variable occurs once either complemented or uncomplemented X Y F minterm 0 0 1 X’. Y’ 0 1 0 X’. Y 1 0 1 X. Y’ 1 1 1 X. Y Sum of minterms form: F(X, Y) = X’. Y’ + X. Y F(X, Y) = Σ(0, 2, 3) – 32 – (sum of minterms m, with F(m)=1 CSCE 211 H Fall 2015

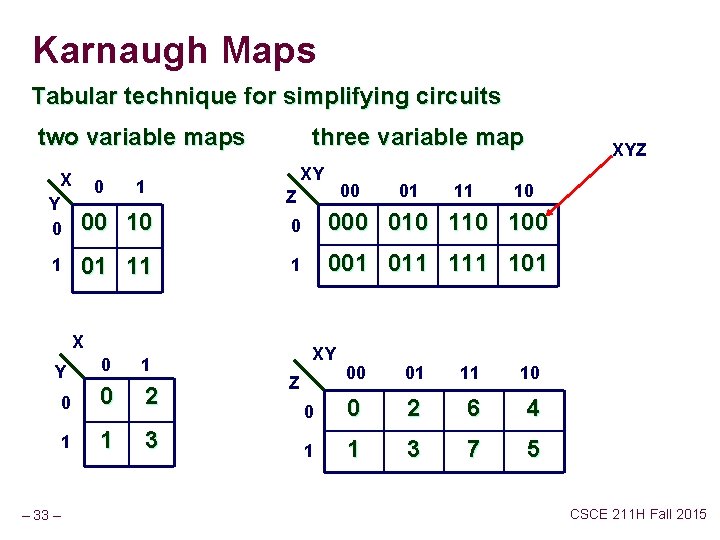
Karnaugh Maps Tabular technique for simplifying circuits two variable maps X 0 1 three variable map XY 00 Z 01 11 XYZ 10 Y 0 00 10 0 000 010 100 1 01 11 1 001 011 101 X Y 0 1 0 0 2 1 1 3 – 33 – XY 00 01 11 10 0 0 2 6 4 1 1 3 7 5 Z CSCE 211 H Fall 2015

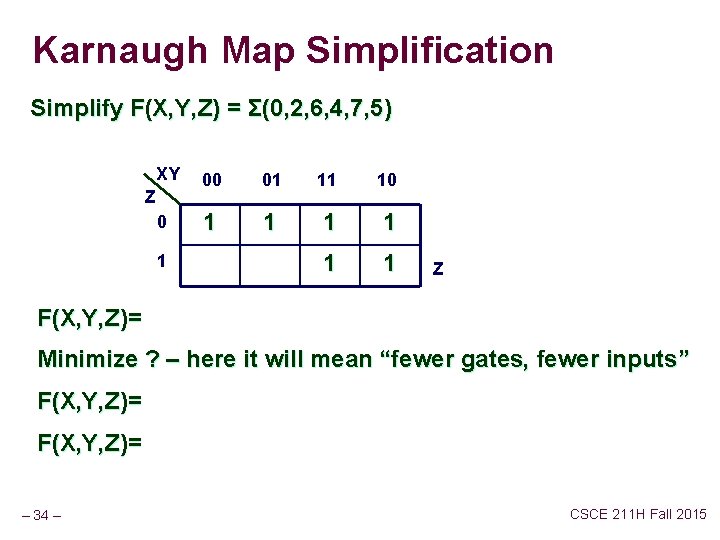
Karnaugh Map Simplification Simplify F(X, Y, Z) = Σ(0, 2, 6, 4, 7, 5) XY 00 01 11 10 0 1 1 1 Z 1 Z F(X, Y, Z)= Minimize ? – here it will mean “fewer gates, fewer inputs” F(X, Y, Z)= – 34 – CSCE 211 H Fall 2015

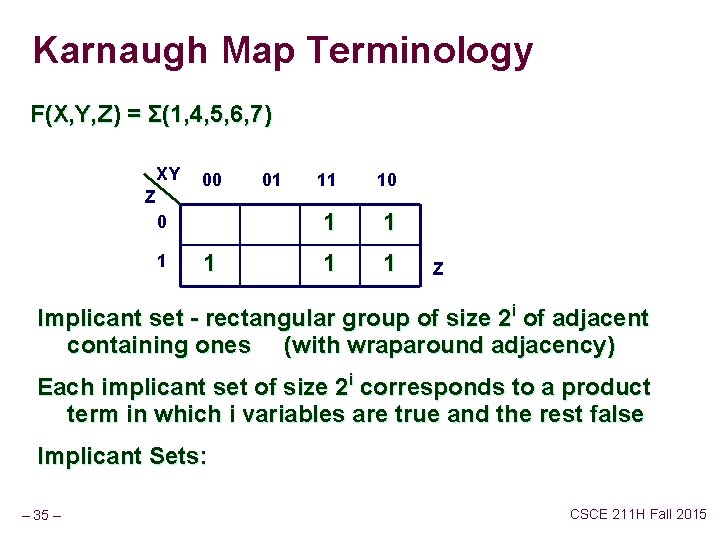
Karnaugh Map Terminology F(X, Y, Z) = Σ(1, 4, 5, 6, 7) XY Z 00 0 1 1 01 11 10 1 1 Z Implicant set - rectangular group of size 2 i of adjacent containing ones (with wraparound adjacency) Each implicant set of size 2 i corresponds to a product term in which i variables are true and the rest false Implicant Sets: – 35 – CSCE 211 H Fall 2015

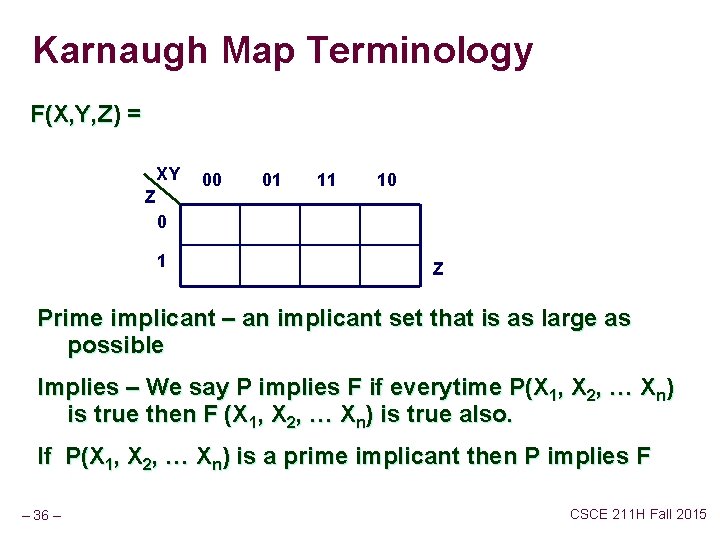
Karnaugh Map Terminology F(X, Y, Z) = XY Z 00 01 11 10 0 1 Z Prime implicant – an implicant set that is as large as possible Implies – We say P implies F if everytime P(X 1, X 2, … Xn) is true then F (X 1, X 2, … Xn) is true also. If P(X 1, X 2, … Xn) is a prime implicant then P implies F – 36 – CSCE 211 H Fall 2015

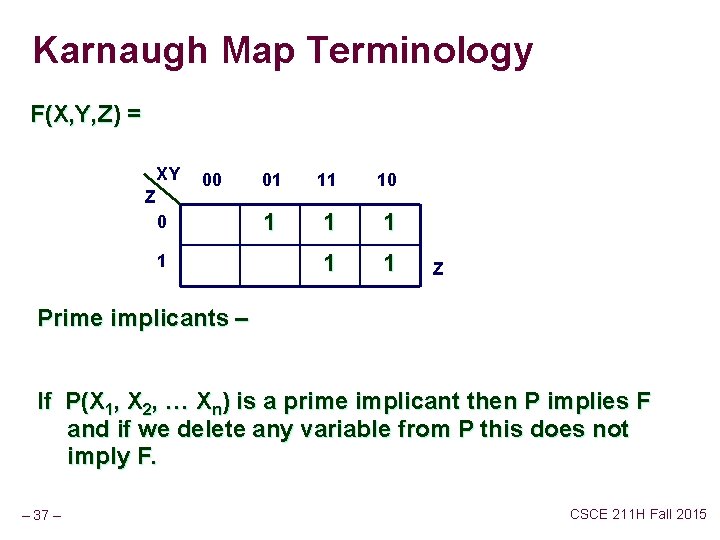
Karnaugh Map Terminology F(X, Y, Z) = XY Z 00 0 1 01 11 10 1 1 1 Z Prime implicants – If P(X 1, X 2, … Xn) is a prime implicant then P implies F and if we delete any variable from P this does not imply F. – 37 – CSCE 211 H Fall 2015

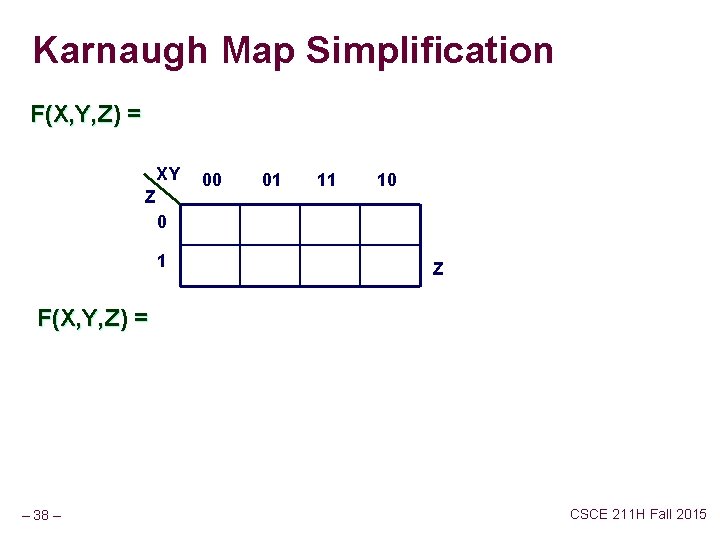
Karnaugh Map Simplification F(X, Y, Z) = XY Z 00 01 11 10 0 1 Z F(X, Y, Z) = – 38 – CSCE 211 H Fall 2015

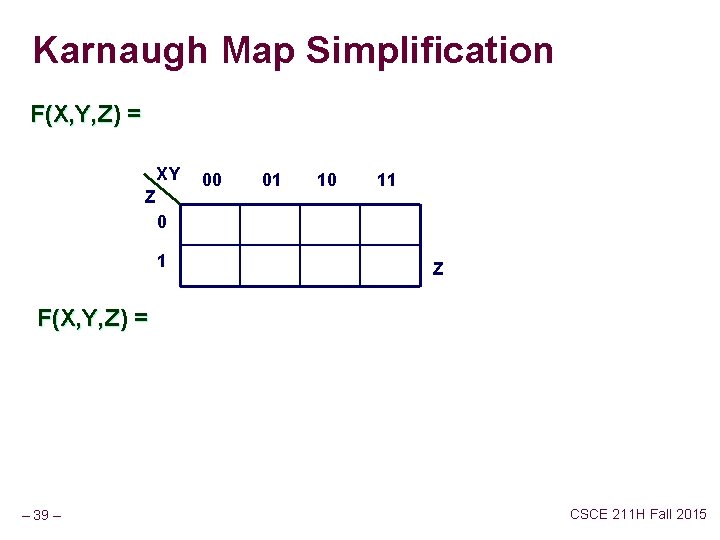
Karnaugh Map Simplification F(X, Y, Z) = XY Z 00 01 10 11 0 1 Z F(X, Y, Z) = – 39 – CSCE 211 H Fall 2015

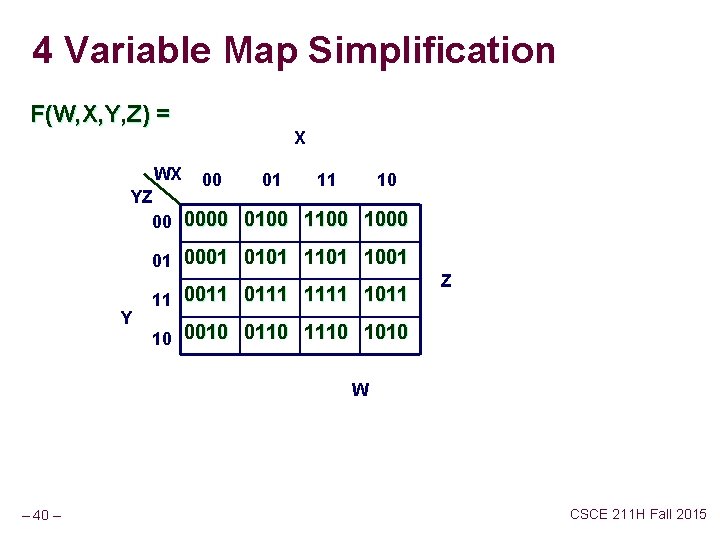
4 Variable Map Simplification F(W, X, Y, Z) = WX X 00 01 11 10 YZ 00 0000 0100 1000 01 0001 0101 1001 Y 11 0011 0111 1011 Z 10 0010 0110 1010 W – 40 – CSCE 211 H Fall 2015

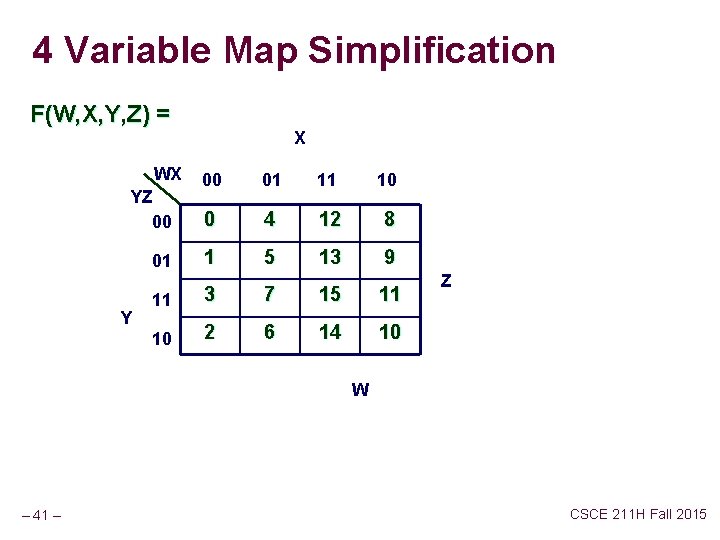
4 Variable Map Simplification F(W, X, Y, Z) = WX 00 01 11 10 0 4 12 8 01 1 5 13 9 11 3 7 15 11 10 2 6 14 10 YZ 00 Y X Z W – 41 – CSCE 211 H Fall 2015

Products-of-Sums What is the delay of products-of-sums circuit? – 42 – CSCE 211 H Fall 2015