CSCD 300 Data Structures Donald Shells Sorting Algorithm

CSCD 300 Data Structures Donald Shell’s Sorting Algorithm Originally developed by Bill Clark, modified by Tom Capaul and Tim Rolfe 1

Shell Sort - Introduction More properly, Shell’s Sort Created in 1959 by Donald Shell Link to a local copy of the article: Donald Shell, “A High-Speed Sorting Procedure”, Communications of the ACM Vol 2, No. 7 (July 1959), 30 -32 Originally Shell built his idea on top of Bubble Sort (link to article flowchart), but it has since been transported over to Insertion Sort. 2

Shell Sort -General Description Essentially a segmented insertion sort Divides an array into several smaller noncontiguous segments The distance between successive elements in one segment is called a gap. Each segment is sorted within itself using insertion sort. Then resegment into larger segments (smaller gaps) and repeat sort. Continue until only one segment (gap = 1) - final sort finishes array sorting. 3

Shell Sort -Background General Theory: Makes use of the intrinsic strengths of Insertion sort is fastest when: The array is nearly sorted. The array contains only a small number of data items. Shell sort works well because: It always deals with a small number of elements. Elements are moved a long way through array with each swap and this leaves it more nearly sorted. 4

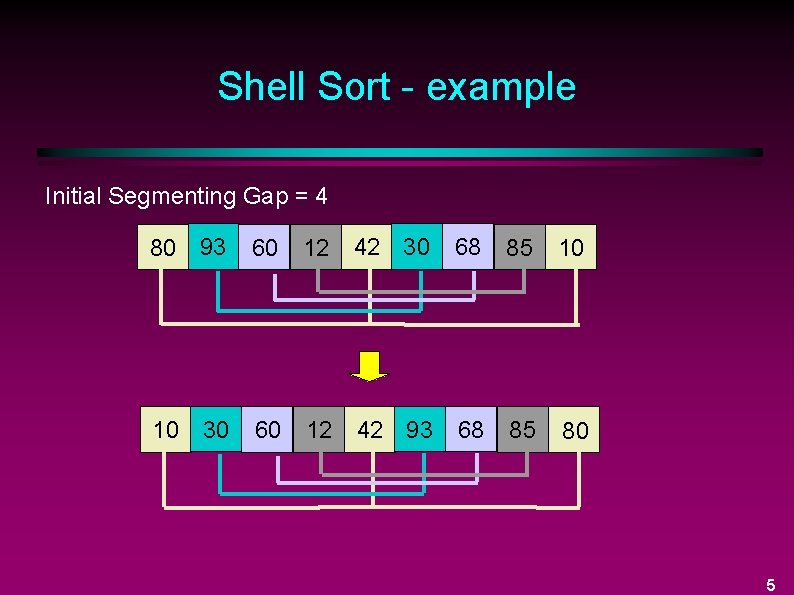
Shell Sort - example Initial Segmenting Gap = 4 80 93 60 12 42 30 68 85 10 10 30 60 12 42 93 68 85 80 5

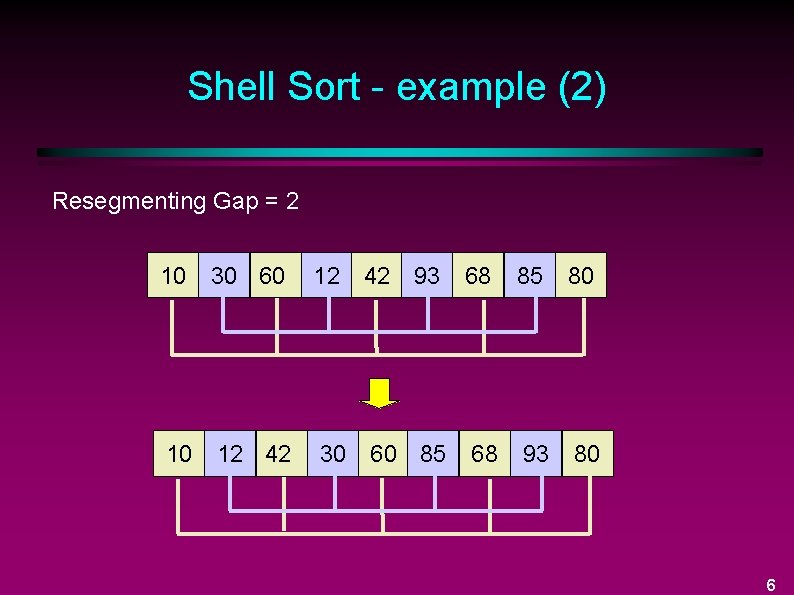
Shell Sort - example (2) Resegmenting Gap = 2 10 30 60 12 42 93 68 85 80 10 12 42 30 68 93 80 60 85 6

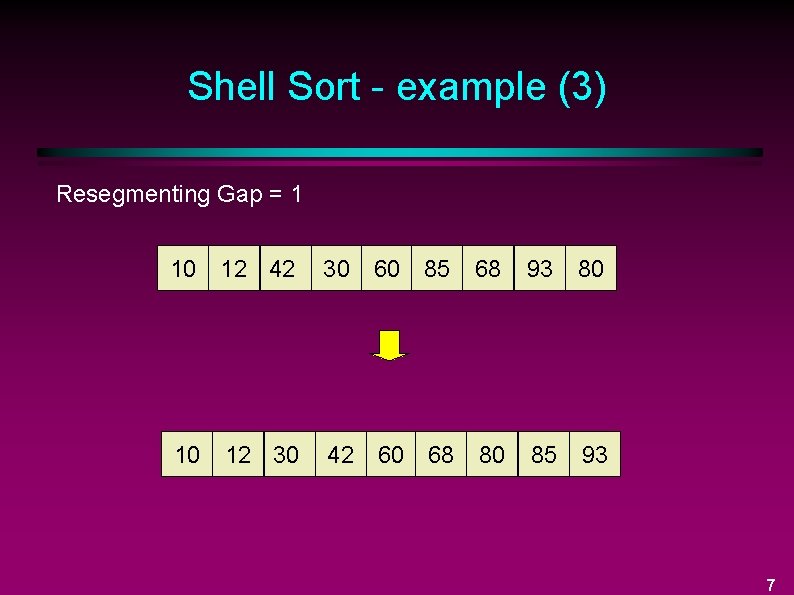
Shell Sort - example (3) Resegmenting Gap = 1 10 12 42 30 60 85 68 93 80 10 12 30 42 60 68 80 85 93 7

Gap Sequences for Shell Sort The sequence h 1, h 2, h 3, . . . , ht is a sequence of increasing integer values which will be used as a sequence (from right to left) of gap values. Any sequence will work as long as it is increasing and h 1 = 1. For any gap value hk we have A[i] <= A[i + hk] An array A for which this is true is hk sorted. An array which is hk sorted and is then hk-1 sorted remains hk sorted. 8

Shell Sort - Ideal Gap Sequence Although any increasing sequence will work ( if h 1 = 1): Best results are obtained when all values in the gap sequence are relatively prime (sequence does not share any divisors). Obtaining a relatively prime sequence is often not practical in a program so practical solutions try to approximate relatively prime sequences. 9

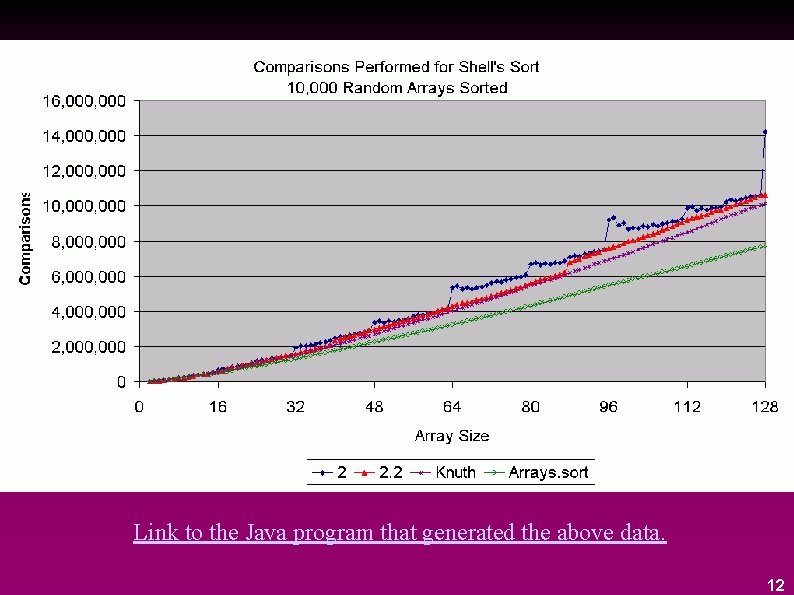
Shell Sort - Practical Gap Sequences Three possibilities presented: 1) Shell's suggestion - first gap is N/2 - successive gaps are previous value divided by 2. Odd gaps only - like Shell method except if division produces an even number add 1. better performance than 1) since all odd values eliminates the factor 2. 2. 2 method - like Odd gaps method (add 1 to even division result) but use a divisor of 2. 2 and truncate. best performance of all - most nearly a relatively prime sequence. 10

Shell Sort - Added Gap Sequence Donald Knuth, in his discussion of Shell’s Sort, recommended another sequence of gaps. h 0 = 1 hj+1 = hj * 3 + 1 Find the hj > n, then start with hj/3 11

Link to the Java program that generated the above data. 12

Shell Sort - Time Complexity Time complexity: O(nr) with 1 < r < 2 This is better than O(n 2) but generally worse than O(n log 2 n). 13

Shellsort - Code public static void shell. Sort( Comparable[ ] the. Array, int n ) { // shell. Sort: sort first n items in array the. Array for( int gap = n / 2; gap > 0; gap = gap / 2 ) for( int i = gap; i < n; i++ ) { Comparable tmp = the. Array[ i ]; int j = i; for( ; j >= gap && tmp. compare. To(the. Array[ j - gap ]) < 0 ; j -= gap ) the. Array[ j ] = the. Array[ j - gap ]; the. Array[ j ] = tmp; } } 14

Shell. Sort -Trace (gap = 4) [0] [2] [3] [4] [5] [6] the. Array 80 93 60 12 42 30 68 n: 9 gap: 4 [1] [7] 85 [8] 10 i: j: for( int gap = n / 2; gap > 0; gap = gap / 2 ) for( int i = gap; i < n; i++ ) { Comparable tmp = the. Array[ i ]; int j = i; for( ; j >= gap && tmp. compare. To(the. Array[ j - gap ]) < 0 ; j -= gap ) the. Array[ j ] = the. Array[ j - gap ]; the. Array[ j ] = tmp; } 15

Shell. Sort -Trace (gap = 2) [0] [1] [2] [3] [4] [5] [6] the. Array 10 30 60 12 42 93 68 n: 9 gap: 2 i: j: [7] 85 [8] 80 for( int gap = n / 2; gap > 0; gap = gap / 2 ) for( int i = gap; i < n; i++ ) { Comparable tmp = the. Array[ i ]; int j = i; for( ; j >= gap && tmp. compare. To(the. Array[ j - gap ]) < 0 ; j -= gap ) the. Array[ j ] = the. Array[ j - gap ]; the. Array[ j ] = tmp; } 16

Shell. Sort -Trace (gap = 1) [0] [1] [2] [3] [4] [5] [6] the. Array 10 12 42 30 60 85 68 n: 9 gap: 1 i: j: [7] 93 [8] 80 for( int gap = n / 2; gap > 0; gap = gap / 2 ) for( int i = gap; i < n; i++ ) { Comparable tmp = the. Array[ i ]; int j = i; for( ; j >= gap && tmp. compare. To(the. Array[ j - gap ]) < 0 ; j -= gap ) the. Array[ j ] = the. Array[ j - gap ]; the. Array[ j ] = tmp; } 17