CSC470 ARTIFICIAL INTELLIGENCE https sites google comsitemtsiddiquecsai Department

CSC-470: ARTIFICIAL INTELLIGENCE https: //sites. google. com/site/mtsiddiquecs/ai Department of Computer Science Lecture 2: Problem Solving by Search

Outline Problem Solving Agent Problem Examples Uninformed search � Problem formulation � Search strategies: depth-first, breadth-first Informed search � Search strategies: best-first, A* � Heuristic functions © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 2

Problem Solving Agent Goal formulation, based on the current situation and performance measure Problem formulation is the process of deciding what actions and states to consider, given a goal. an agent with several options can decide what to do by first examining different possible sequences of actions that lead to states of known value, and then choosing the best sequence. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 3

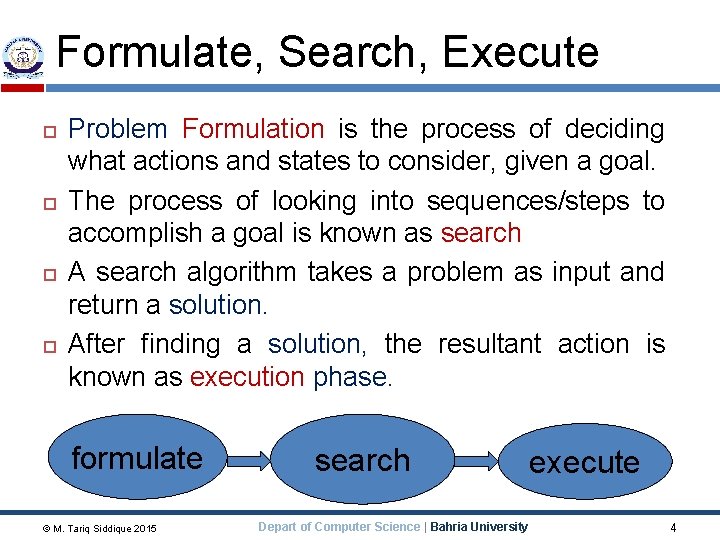
Formulate, Search, Execute Problem Formulation is the process of deciding what actions and states to consider, given a goal. The process of looking into sequences/steps to accomplish a goal is known as search A search algorithm takes a problem as input and return a solution. After finding a solution, the resultant action is known as execution phase. formulate © M. Tariq Siddique 2015 search execute Depart of Computer Science | Bahria University 4

A Simple Problem-Solving Agent function SIMPLE-PROBLEM-SOLVING-AGENT( percept) returns an action persistent: seq, an action sequence, initially empty state, some description of the current world state goal, a goal, initially null problem, a problem formulation state UPDATE-STATE(state, percept) if seq is empty then goal FORMULATE-GOAL(state) problem FORMULATE-PROBLEM(state, goal) seq SEARCH(problem) If seq = failure then return a null action FIRST(seq) seq REST(seq) return action © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 5

Problem Solving By Search 6 Represent the problem as STATES and OPERATORS that transform one state into another state. A solution to the problem is an OPERATOR SEQUENCE that transforms the INITIAL STATE into a GOAL STATE. Finding the sequence requires SEARCHING the STATE SPACE by GENERATING the paths connecting the two. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 6

Search By Generating States 7 Initial State 3 2 1 5 4 6 Operations 100 Goal State 1 2 6 5 1 6 3 5 2 3 5 4 2 5 © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 7

Basic Concepts State: finite representation of the world at a given time. Operator(action formulation): a function that transforms a state into another (also called rule, transition, successor function, production, action) Initial state: world state at the beginning. Goal state: desired world state (can be several) Goal test: test to determine if the goal has been reached. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 8

Basic Concepts (Cont. . ) Reachable goal: a state for which there exists a sequence of operators to reach it. State space: set of all reachable states from initial state (possibly infinite). Cost function: a function that assigns a cost to each operation. Performance: � cost of the final operator sequence (path cost) � cost of finding the sequence © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 9

Problem Solving Agents (Example) Goal Formulation � Based on the current situation and agent’s performance measure E. g. Going from Los Angeles to Las Vegas Problem Formulation � What actions and states to consider, given a goal � Not too detail, not to broad E. g. Driving from Los Angeles to Las Vegas � If unknown environment, take random action � Observable environment know current state (location) � Discrete environment at any given state, only finitely many actions to choose from � Deterministic environment each action has exactly one outcome Solution � Action sequence © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 10

© M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 11

Problem-Solving Agent (Example) function SIMPL-PROBLEM-SOLVING-AGENT( percept) returns an action persistent: seq, an action sequence, initially empty state, some description of the current world state goal, a goal, initially null problem, a problem formulation // What is the current state? state UPDATE-STATE(state, percept) // From LA to Vegas (given current state) if seq is empty then // e. g. , Gas usage goal FORMULATE-GOAL(state) problem FORMULAE-PROBLEM(state, goal) seq SEARCH(problem) // If fails to reach goal, update If seq = failure then return a null action FIRST(seq) seq REST(seq) return action © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 12

Problems (Example) Initial state : state that agent starts in � In(Los Angeles) Actions : applicable functions to the agents � {Go (Long Beach), Go(Santa Clarita), Go(San Bernardino)} Transition model: what each action does (result) � RESULT(In(Los Angeles), Go (Long Beach)) = In(Long Beach) State space = initial state + actions + transition model � Represent in a graph form � Path = sequence of states connected by a sequence of actions Goal test: check whether a given state is a goal state Path cost, step cost Solution: an action sequence that leads from the initial state to a goal state. Optimal solution: the lowest path cost among all solutions © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 13

Example Problems Toy problems � The Maze � The 8 and 15 -puzzle � The 8 -queen/nqueens � Cryptarithmetic � Robotic Assembly � The vacuum world � Missionaries and cannibals � The River Problem � Water Jugs © M. Tariq Siddique 2015 § Real-world problems § Route finding § Touring and travelling salesperson § VLSI layout § Robot navigation § Assembly sequencing Depart of Computer Science | Bahria University 14

The Maze A maze can be represented as a state space Initial state Each state represents “where you are” in the maze � The start state represents your starting position � The goal state represents the exit from the maze � Operators (for a rectangular maze) are: move north, move south, move east, and move west Each operator takes you to a new state (maze location) � Operators may not always apply, because of walls in the maze � © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University Goal state 15

The 8 and 15 -puzzle The 8 -puzzle is a small single board player game: Tiles are numbered 1 through 8 and one blank space on a 3 x 3 board. A 15 -puzzle, using a 4 x 4 board, is commonly sold as a child's puzzle. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 16

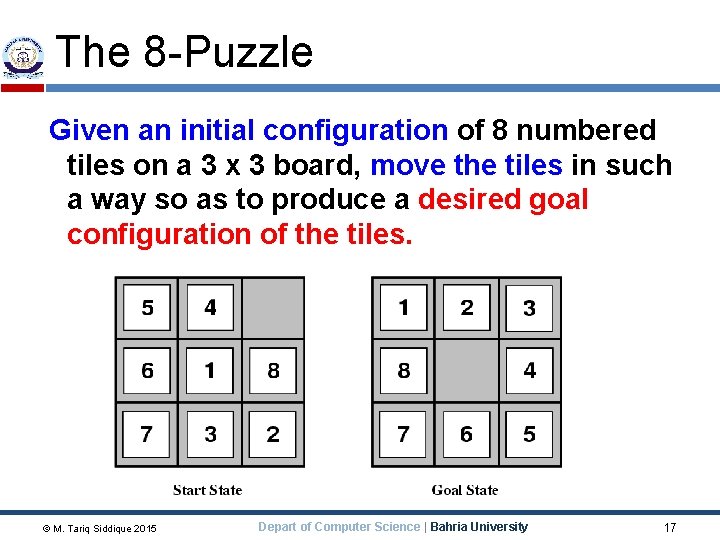
The 8 -Puzzle Given an initial configuration of 8 numbered tiles on a 3 x 3 board, move the tiles in such a way so as to produce a desired goal configuration of the tiles. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 17

The 8 -Puzzle (Cont) States: Integer location of tiles (ignore intermediate positions) Operators: Move blank left, right, up, down Goal Test: goal state (given) Path Cost: 1 per move Constraints: Can only move blank in a direction if it stays in puzzle © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 18

The 8 -Puzzle (Cont) States: a state description specifies the location of each of the eight tiles in one of the nine squares. Operators: blank moves left, right, up, , or down. Goal test: state matches the goal configuration shown in the right. Path: each step costs 1, so that the path cost is just the length of the path. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 19

The 8 -Puzzle (Cont) ¬ ® ¯ 1 5 4 6 1 8 7 3 2 Goal: 7 5 4 6 1 8 7 3 2 © M. Tariq Siddique 2015 ® 5 4 6 1 8 7 3 2 8 3 4 6 5 ¯ ¬ ¬ 2 5 4 8 6 1 7 3 2 ¬ ¯ 5 1 4 6 8 7 3 2 5 4 8 6 1 7 3 2 ¯ 5 4 8 6 1 2 7 3 Depart of Computer Science | Bahria University 5 4 6 1 8 7 3 2 20

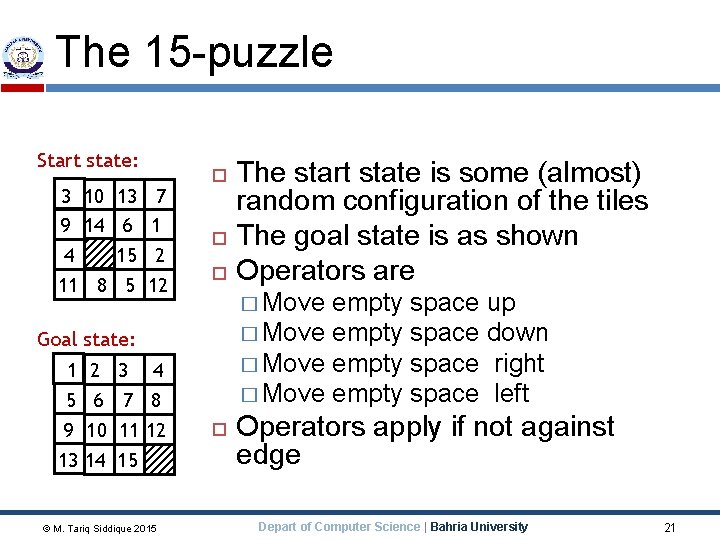
The 15 -puzzle Start state: 3 10 9 14 4 11 8 13 6 15 5 7 1 2 12 � Move empty space up � Move empty space down � Move empty space right � Move empty space left Goal state: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 © M. Tariq Siddique 2015 The start state is some (almost) random configuration of the tiles The goal state is as shown Operators are Operators apply if not against edge Depart of Computer Science | Bahria University 21

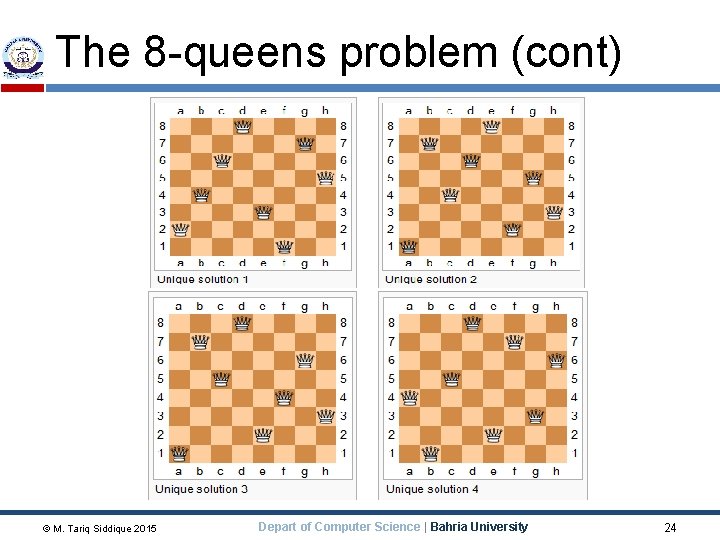
The 8 -queens problem The objective is to place eight queens on a chessboard such that no queen threatens another. A queen threatens another queen in the same row, column or in diagonal In this example, the two queens on the corners are the only queens threatening each other. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 22

The 8 -queens problem (cont) The states and operators for this problem could be: � States: any arrangement of 0 to 8 queens on the board. � Operators: add a queen to any square. This is a bad choice because there are 64^8 possible sequences to investigate. A better formulation would be to choose a smarter operator that States: any arrangement of 0 to 8 queens on the board. � Operators: place a queen in the left-most empty column such that it is not attacked by any other queen. � © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 23

The 8 -queens problem (cont) © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 24

Robotic Assembly states: real-valued coordinates of robot joint angles parts of the object to be assembled operators: continuous motions of robot joints goal test: complete assembly with no robot included! path cost: time to execute © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 25

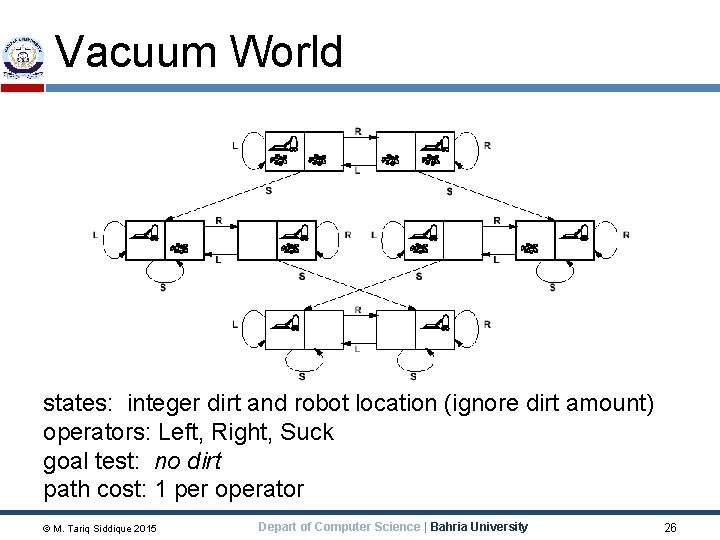
Vacuum World states: integer dirt and robot location (ignore dirt amount) operators: Left, Right, Suck goal test: no dirt path cost: 1 per operator © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 26

Cryptarithmetic Problem • States: a cryptarithmetic puzzle with some letters replaced by digits • Operators: replace all occurrences of a letter with a digit not already appearing in the puzzle. • Goal test: puzzle contains only digits, and represents a correct sum. • Path cost: zero. All solutions equally valid. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 27

Cryptarithmetic Problem (cont. . ) The puzzle SEND + MORE = MONEY, after solving, will appear like this: SEND 9 56 7 +MORE 1 0 8 5 ---------MONEY 1 0 6 52 © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 28

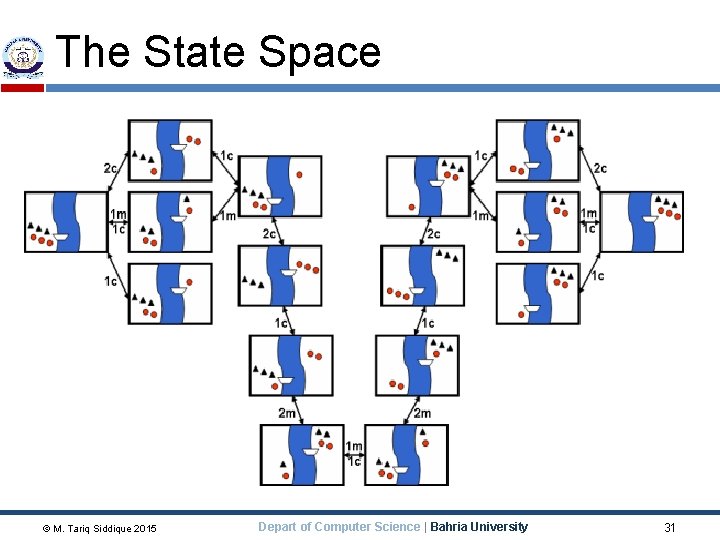
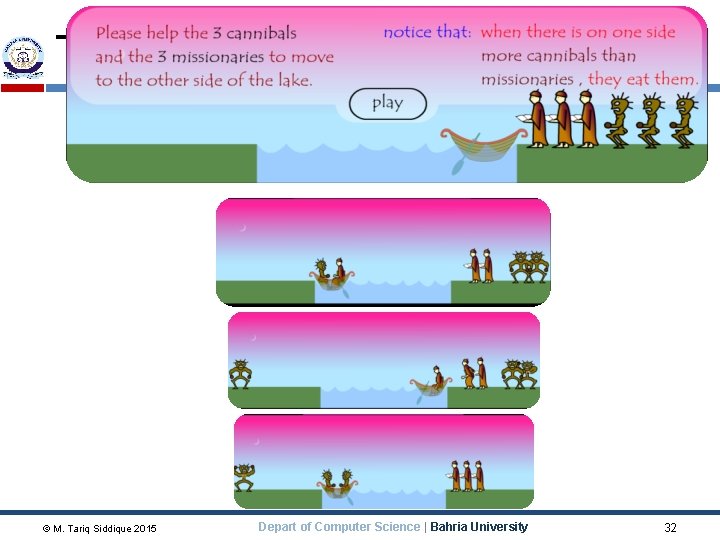
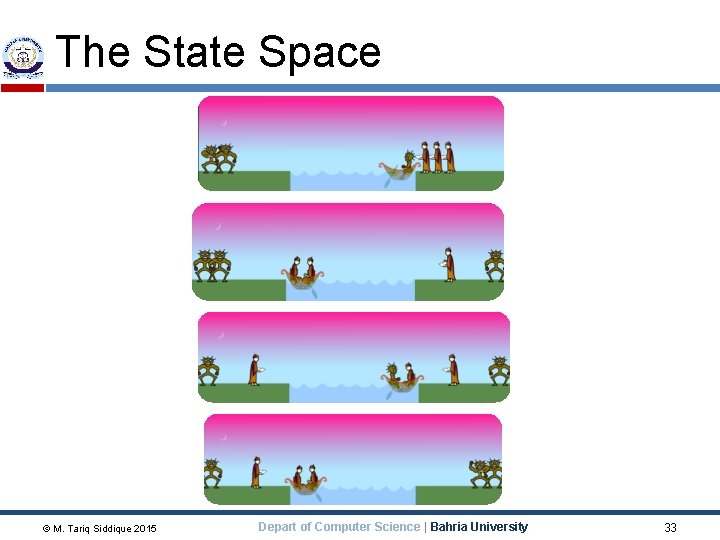
Missionaries and Cannibals An old puzzle is the “Missionaries and cannibals” problem (in various guises) The missionaries and cannibals wish to cross a river They have a canoe that can hold two people It is unsafe to have cannibals outnumber missionaries M M C C C M Initial state © M. Tariq Siddique 2015 M M C C C M Goal state Depart of Computer Science | Bahria University 29

Operations An operation takes us from one state to another Here are five possible operations: � Canoe takes 1 missionary across river (1 m) � Canoe takes 1 cannibal across river (1 c) � Canoe takes 2 missionaries across river (2 m) � Canoe takes 2 cannibals across river (2 c) � Canoe takes 1 missionary and 1 cannibal across river (1 m 1 c) We don’t have to specify “west to east” or “east to west” because only one of these will be possible at any given time © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 30

The State Space © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 31

The State Space © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 32

The State Space © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 33

© M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 34

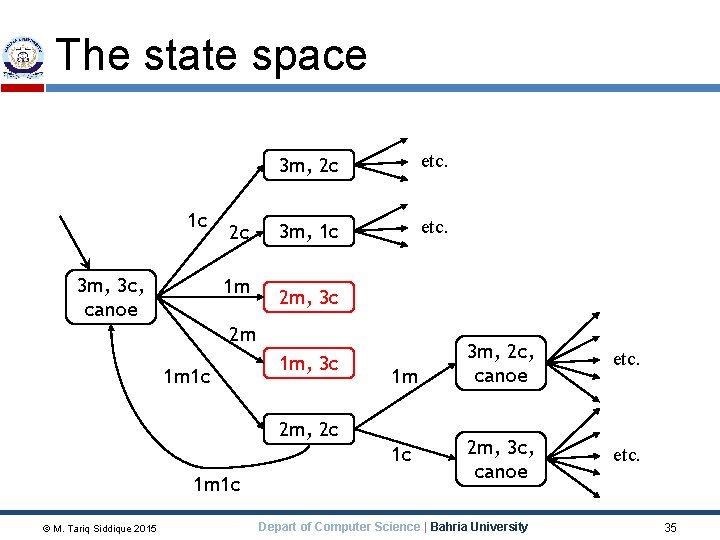
The state space 35 1 c 3 m, 3 c, canoe 2 c 1 m 3 m, 2 c etc. 3 m, 1 c etc. 2 m, 3 c 2 m 1 m 1 c 1 m, 3 c 1 m 2 m, 2 c 1 c 1 m 1 c © M. Tariq Siddique 2015 3 m, 2 c, canoe etc. 2 m, 3 c, canoe etc. Depart of Computer Science | Bahria University 35

Missionaries and Cannibals Solution Near side 0 1 2 3 4 5 6 7 8 9 side Initial setup: MMMCCC Two cannibals cross over: MMMC One comes back: MMMCC Two cannibals go over again: MMM CCC One comes back: MMMC Two missionaries cross: MC MMCC A missionary & cannibal return: MMCC Two missionaries cross again: CC MMMC A cannibal returns: CCC MMM Two cannibals cross: C Depart of Computer Science | Bahria University © M. Tariq Siddique 2015 Far B B B CC C B B CC B B MC B B B 36

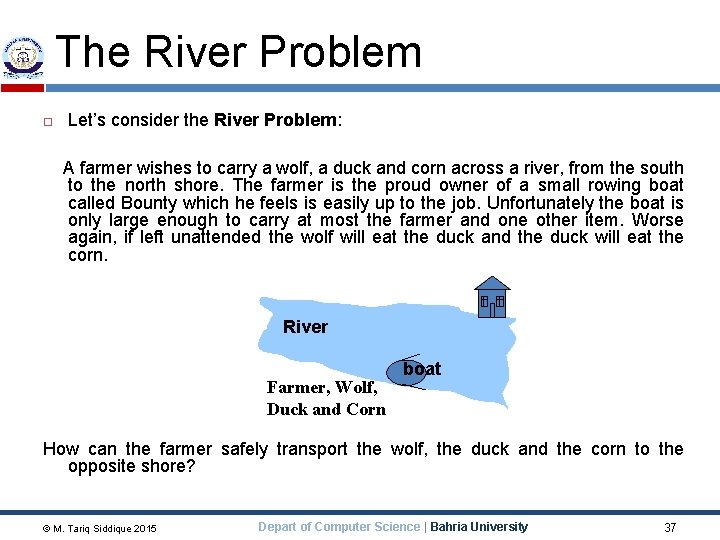
The River Problem Let’s consider the River Problem: A farmer wishes to carry a wolf, a duck and corn across a river, from the south to the north shore. The farmer is the proud owner of a small rowing boat called Bounty which he feels is easily up to the job. Unfortunately the boat is only large enough to carry at most the farmer and one other item. Worse again, if left unattended the wolf will eat the duck and the duck will eat the corn. River Farmer, Wolf, Duck and Corn boat How can the farmer safely transport the wolf, the duck and the corn to the opposite shore? © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 37

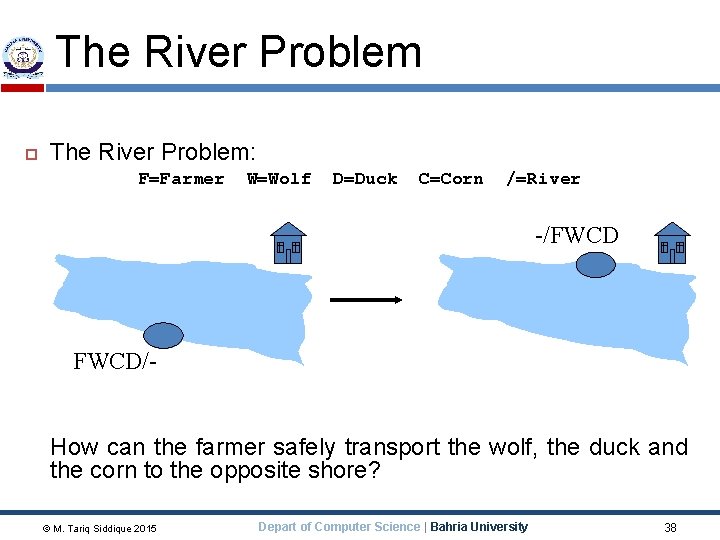
The River Problem The River Problem: F=Farmer W=Wolf D=Duck C=Corn /=River -/FWCD/How can the farmer safely transport the wolf, the duck and the corn to the opposite shore? © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 38

The River Problem formulation: � State representation: location of farmer and items in both sides of river [items in South shore / items in North shore] : (FWDC/-, FD/WC, C/FWD …) � Initial State: farmer, wolf, duck and corn in the south shore � Goal State: farmer, duck and corn in the north shore -/FWDC � Operators: the farmer takes in the boat at most one item from one side to the other side (F-Takes-W, F-Takes-D, F-Takes-C, F-Takes-Self [himself only]) � Path cost: the number of crossings © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University FWDC/- 39

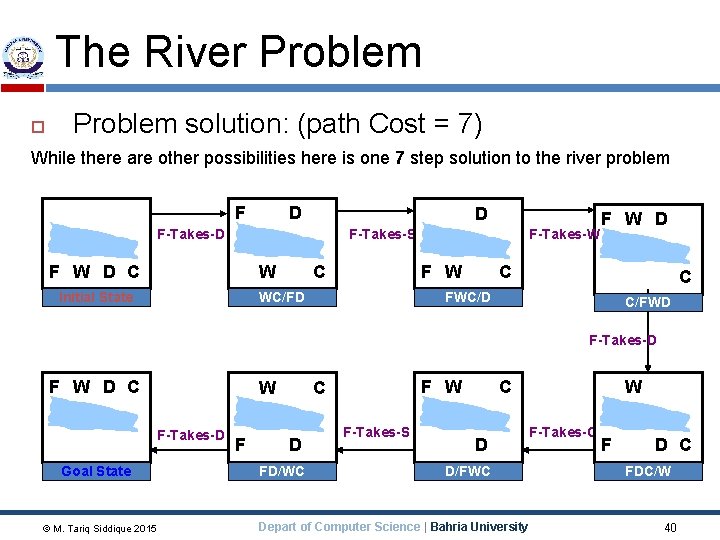
The River Problem solution: (path Cost = 7) While there are other possibilities here is one 7 step solution to the river problem F D D F-Takes-S F W D C W C F W WC/FD Initial State F-Takes-W F W D C C FWC/D C/FWD F-Takes-D F W D C W F-Takes-D Goal State © M. Tariq Siddique 2015 F F W C D FD/WC F-Takes-S C D W F-Takes-C D/FWC Depart of Computer Science | Bahria University F D C FDC/W 40

Water Jugs You’re given � A spigot � A 3 Gallon jug � A 4 Gallon jug The goal: Get 2 gallons of water in the 4 Gallon jug. Actions: Filling jugs from spigot, dumping water in jugs onto ground, dumping 4 gallon into 3 gallon jug until 3 gallon jug is full. Dumping 3 gallon jug into 4 gallon jug until empty or until 4 gallon is full, etc. Think of states, actions, goals state, operators and a solution. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 41

Water Jugs States: How full are the two jugs? State Representation 4 G 3 G Initial State: 4 G = 0 3 G=0 Goal State 4 G=2 Constraints 0 4 G 4 0 3 G 3 © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 42

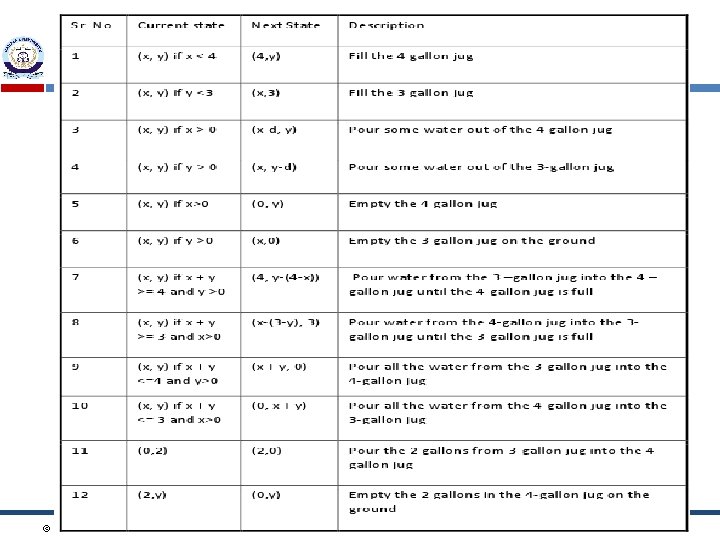
Operators F 3: Fill the 3 Gallon jug from the tap. F 4: Fill the 4 Gallon jug from the tap. E 4: Empty the 4 -Gallon jug on the ground P 43: Pour water from 4 G jug into the 3 G jug until 3 G jug is full P 34: Pour water from 3 G jug into the 4 G jug © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 43

Search Space The state space for this problem can be described as the set of ordered pairs of integers (x, y) such that x = 0, 1, 2, 3 or 4 and y = 0, 1, 2 or 3; x represents the number of gallons of water in the 4 -gallon jug and y represents the quantity of water in 3 -gallon jug Production rules for Water Jug Problem The operators to be used to solve the problem can be described as follows: The start state is (0, 0) The goal state is (2, n) © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 44

© M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 45

States vs. nodes *A state is a (representation of a) physical configuration. *A node is a data structure constituting part of a search tree includes parent, children, depth, path cost g(n). * States do not have parents, children, depth, or path cost! A Node is a data structure with five components: � the state in the state space to which the node corresponds; � the node in search tree that generated this node (this is called the parent node); � the operator that was applied to generate the node; � the number of nodes on the path from the root to this node (the depth of the node); � the path cost of the path from the initial state to the node. Datatype node Depart of Computer Science | Bahria University components: STATE, PARENT-NODE, OPERATOR, DEPTH, PATH-COST © M. Tariq Siddique 2015 46

Nodes and States Node is a data structure to represent search tree for a particular problem State represents a configuration of the world Fringe or frontier � A collection of nodes that are waiting to be expanded � a set of nodes can be represented as a queue with following operations MAKE-QUEUE(Elements) creates a queue with the given elements EMPTY? (Queue) returns true if there are no more elements in the queue. REMOVE-FRONT(Queue) removes the element at the front of the queue and returns it QUEUE-FN(Element, Queue) inserts a set of elements into the queue. Different varieties of the queuing function produce different varieties of the search algorithm © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 47

Implementation of Search Algorithms Nodes: state, parent-node, operator, depth, path cost Function GENERAL-SEARCH (problem, queing-fn) returns a solution or failure nodes MAKE-QUEUE (MAKE-NODE(INITIAL-STATE[problem])) loop do if nodes is empty, then return failure node Remove-Front(nodes) if GOAL-TEST [problem] applied to STATE(node) succeeds then return node else nodes QUEING-FN(nodes, EXPAND(node, operators[problem])) end © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 48

Conclusions Interesting problems can be cast as search problems, but you’ve got to set up state space Problem formulation usually requires abstracting away real world details to define a state space that can feasibly be explored © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 49

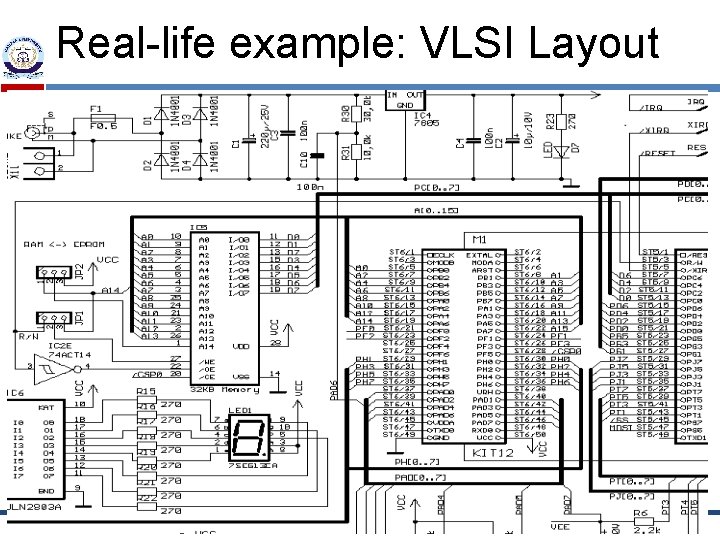
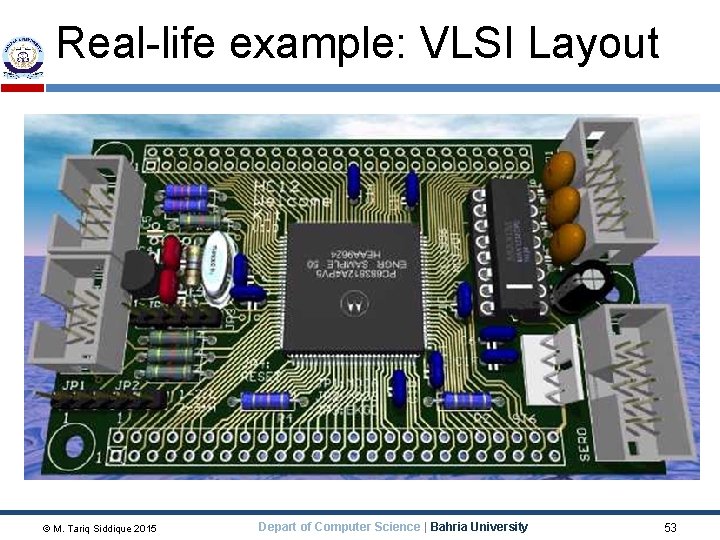
Real-life example: VLSI Layout Ø Ø Ø Given schematic diagram comprising components (chips, resistors, capacitors, etc) and interconnections (wires), find optimal way to place components on a printed circuit board, under the constraint that only a small number of wire layers are available (and wires on a given layer cannot cross!) “optimal way”? ? minimize surface area minimize number of signal layers minimize number of vias (connections from one layer to another) minimize length of some signal lines (e. g. , clock line) distribute heat throughout board etc. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 50

Real-life example: VLSI Layout © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 51

Use automated tools to place components and route wiring. © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 52

Real-life example: VLSI Layout © M. Tariq Siddique 2015 Depart of Computer Science | Bahria University 53