CSC 4170 Theory of Computation Turing Machines Section

CSC 4170 Theory of Computation Turing Machines Section 3. 1

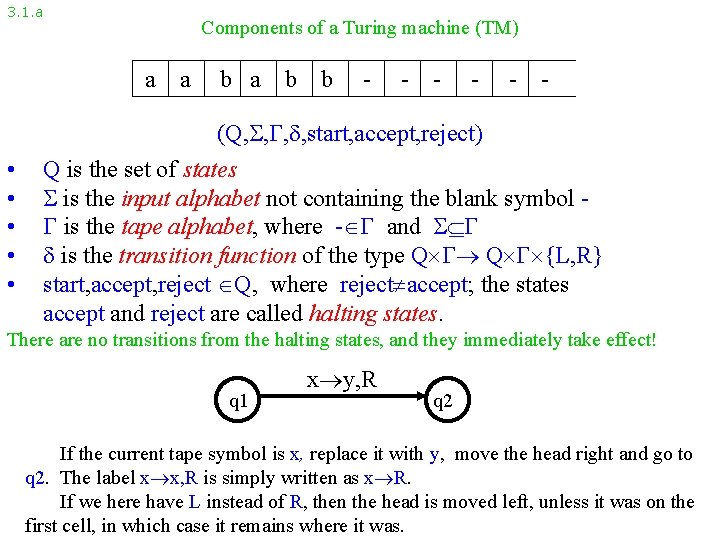
3. 1. a Components of a Turing machine (TM) a a b b - - - (Q, , start, accept, reject) • • • Q is the set of states is the input alphabet not containing the blank symbol is the tape alphabet, where - and is the transition function of the type Q Q {L, R} start, accept, reject Q, where reject accept; the states accept and reject are called halting states. There are no transitions from the halting states, and they immediately take effect! q 1 x y, R q 2 If the current tape symbol is x, replace it with y, move the head right and go to q 2. The label x x, R is simply written as x R. If we here have L instead of R, then the head is moved left, unless it was on the first cell, in which case it remains where it was.

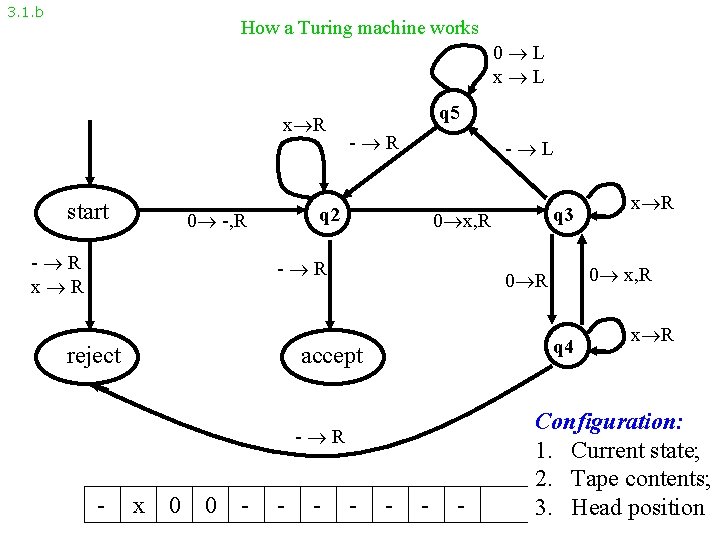
3. 1. b How a Turing machine works 0 L x R start - R - L q 2 0 -, R - R x R q 5 0 x, R - R reject q 4 accept x 0 0 - - - - x R 0 x, R 0 R - q 3 x R Configuration: 1. Current state; 2. Tape contents; 3. Head position

3. 1. c 1 Definitions A TM accepts an input string iff, for this input, sooner or later it enters the accept state. Otherwise the string is considered rejected. Thus, the input is rejected in two cases: 1) The machine enters the reject state at some point, or 2) The machine never halts (never enters a halting state). A Turing machine is said to be a decider iff it halts for every input. The language recognized by a TM --- the set the strings that TM accepts; If this machine is a decider, then we say that it not only recognizes, but also decides that language. A language is said to be Turing-recognizable iff some TM recognizes it. A language is said to be Turing-decidable iff some TM decides it.

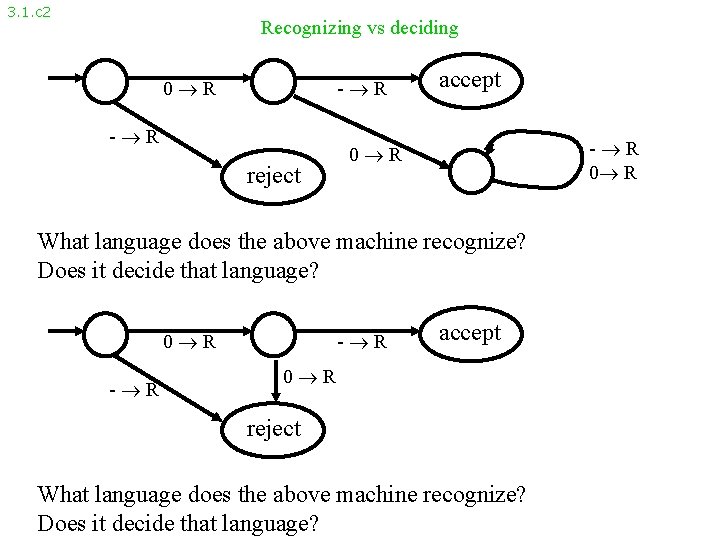
3. 1. c 2 Recognizing vs deciding 0 R - R reject accept - R 0 R What language does the above machine recognize? Does it decide that language? 0 R - R accept 0 R reject What language does the above machine recognize? Does it decide that language?

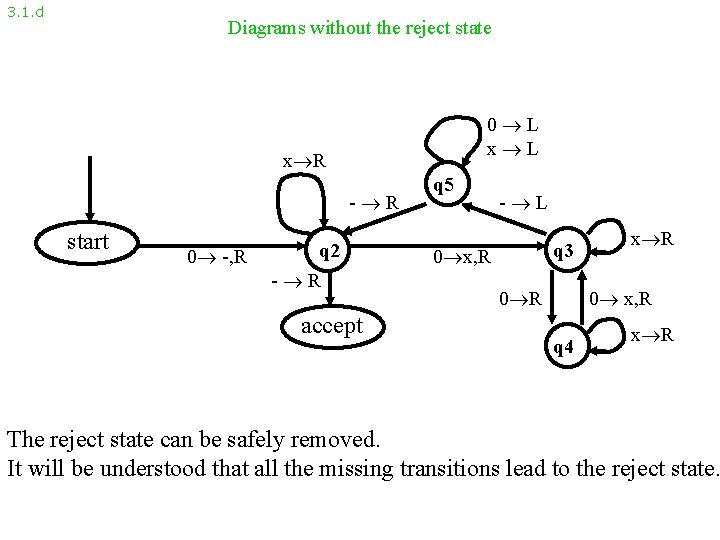
3. 1. d Diagrams without the reject state 0 L x R - R start 0 -, R q 2 - R accept q 5 - L q 3 0 x, R 0 R x R 0 x, R q 4 x R The reject state can be safely removed. It will be understood that all the missing transitions lead to the reject state.

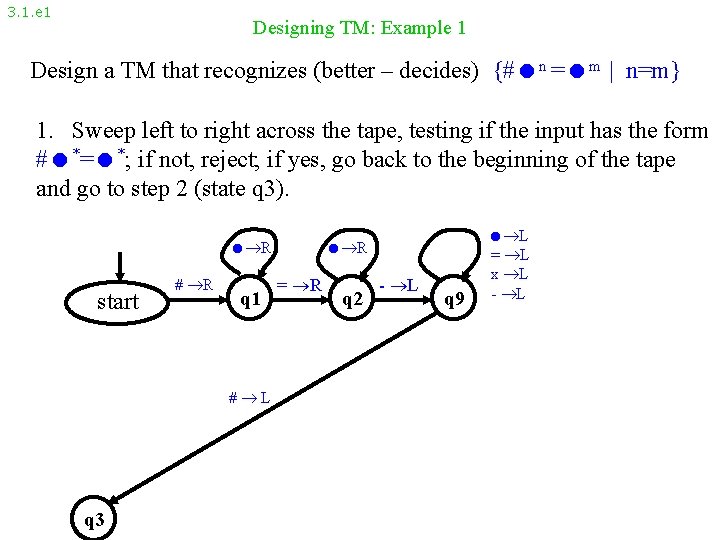
3. 1. e 1 Designing TM: Example 1 Design a TM that recognizes (better – decides) {# n = m | n=m} 1. Sweep left to right across the tape, testing if the input has the form # *= *; if not, reject; if yes, go back to the beginning of the tape and go to step 2 (state q 3). R start # R q 1 # L q 3 R = R q 2 - L q 9 L = L x L - L

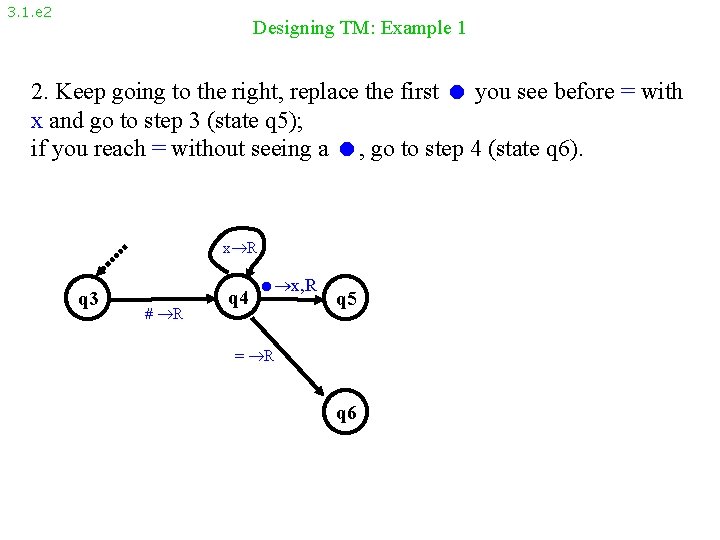
3. 1. e 2 Designing TM: Example 1 2. Keep going to the right, replace the first you see before = with x and go to step 3 (state q 5); if you reach = without seeing a , go to step 4 (state q 6). x R q 3 # R q 4 x, R q 5 = R q 6

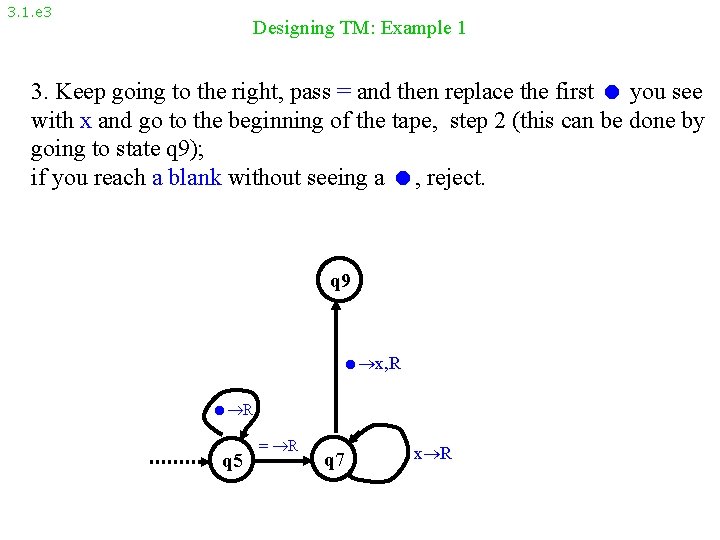
3. 1. e 3 Designing TM: Example 1 3. Keep going to the right, pass = and then replace the first you see with x and go to the beginning of the tape, step 2 (this can be done by going to state q 9); if you reach a blank without seeing a , reject. q 9 x, R R q 5 = R q 7 x R

3. 1. e 4 Designing TM: Example 1 4. Keep going to the right as long as you see x. If you see a before reaching a blank, reject; otherwise accept. x R q 6 - R accept

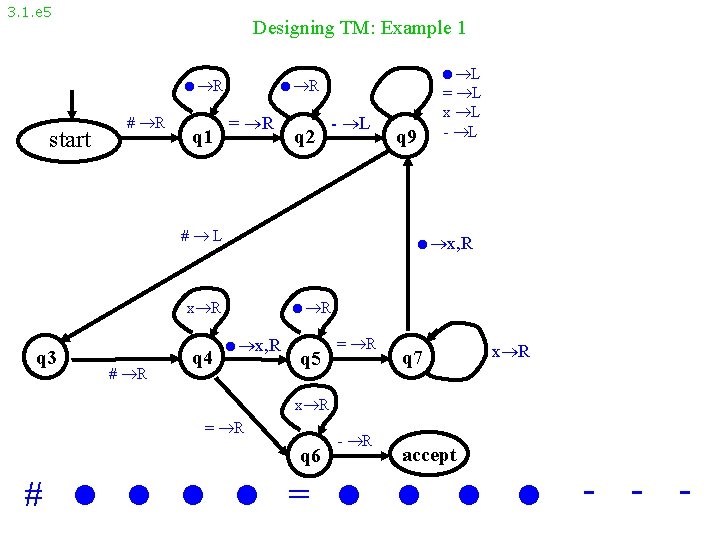
3. 1. e 5 Designing TM: Example 1 R start # R R = R q 1 q 2 - L # L x R q 3 # R q 4 q 9 L = L x L - L x, R R x, R q 5 = R q 7 x R = R q 6 - R accept # = - - -

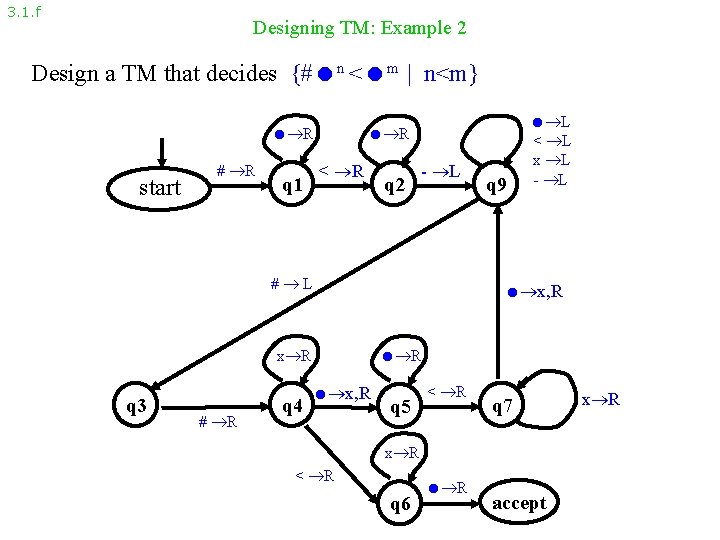
3. 1. f Designing TM: Example 2 Design a TM that decides {# n < m | n<m} R start # R R < R q 1 q 2 - L # L x R q 3 # R q 4 q 9 L < L x L - L x, R R x, R q 5 < R q 7 x R < R q 6 R accept x R

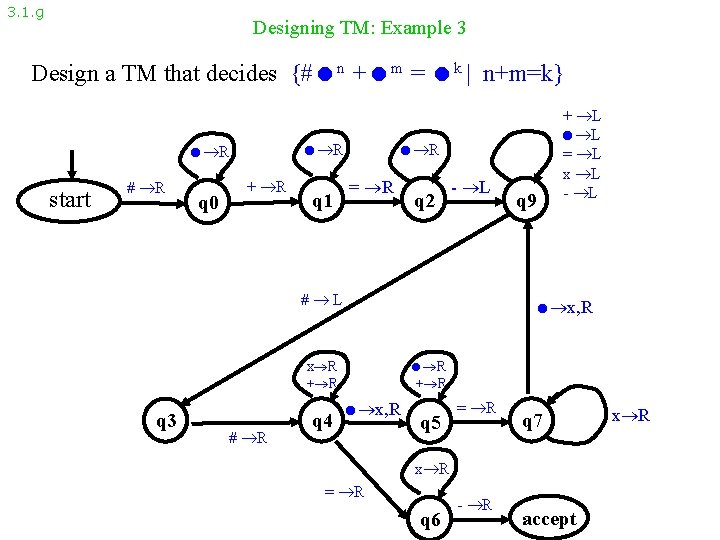
3. 1. g Designing TM: Example 3 Design a TM that decides {# n + m = k | n+m=k} R R start # R q 0 + R R = R q 1 q 2 - L # L x R + R q 3 # R q 4 q 9 + L L = L x L - L x, R R + R x, R q 5 = R q 7 x R = R q 6 - R accept x R

3. 1. h Designing TM: Example 4 Design a TM that decides {# n m = k | n m=k} Step 1: Check if the string has the form # * * = *. If not, reject; If yes, go back to the beginning of the tape, step 2. Step 2: Find the first between # and , delete it and go to step 3; If no such was found, go to step 5. Step 3: Find the first between and =, delete it and go to step 4; If no such was found, go to the beginning of the tape, restoring on the way back all the deleted between and =, and go to step 2. Step 4: Find the first after =, delete it, go back to , and go to step 3; If no such was found before seeing a blank, reject. Step 5: Go right past = ; if no is found there before reaching a blank, Accept; otherwise reject. # = -

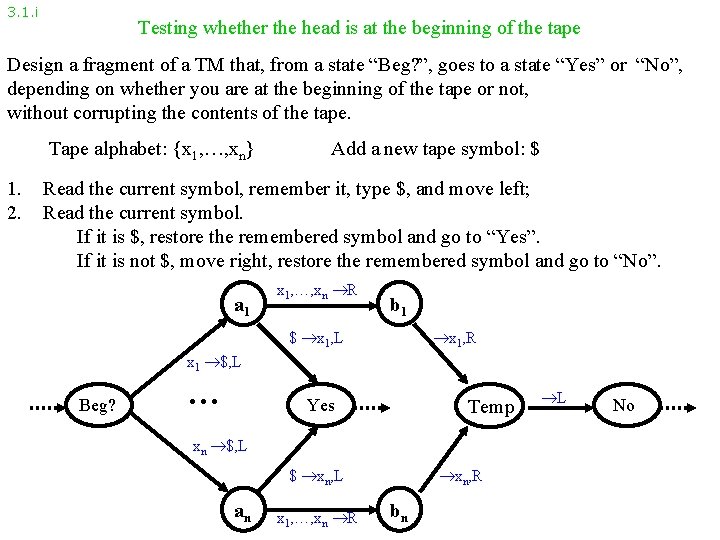
3. 1. i Testing whether the head is at the beginning of the tape Design a fragment of a TM that, from a state “Beg? ”, goes to a state “Yes” or “No”, depending on whether you are at the beginning of the tape or not, without corrupting the contents of the tape. Tape alphabet: {x 1, …, xn} 1. 2. Add a new tape symbol: $ Read the current symbol, remember it, type $, and move left; Read the current symbol. If it is $, restore the remembered symbol and go to “Yes”. If it is not $, move right, restore the remembered symbol and go to “No”. a 1 x 1, …, xn R b 1 $ x 1, L x 1, R x 1 $, L Beg? … Yes Temp xn $, L $ xn, L an x 1, …, xn R xn, R bn L No

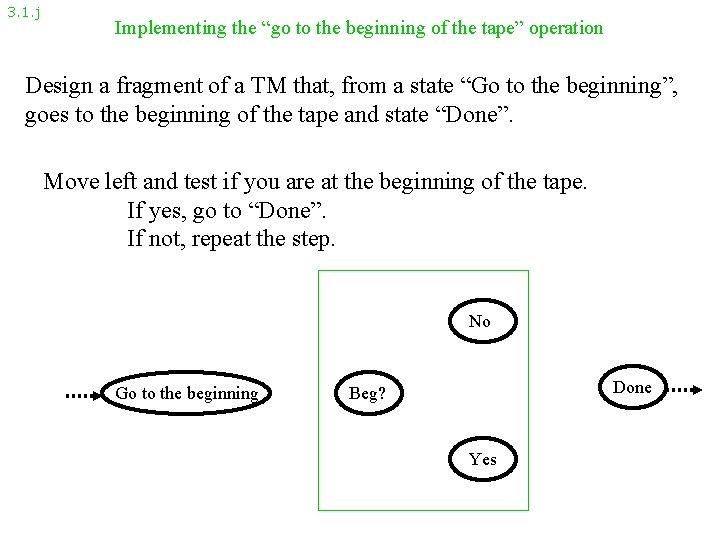
3. 1. j Implementing the “go to the beginning of the tape” operation Design a fragment of a TM that, from a state “Go to the beginning”, goes to the beginning of the tape and state “Done”. Move left and test if you are at the beginning of the tape. If yes, go to “Done”. If not, repeat the step. No Go to the beginning Done Beg? Yes

3. 1. k Shifting tape contents Design a fragment of a TM that types 0 in the current cell and shifts the (old) contents of the remaining tape one cell to the right. Assume the tape alphabet is {0, 1, -}, and that all cells after the leftmost blank cells are also always blank. 1. Read the current symbol, remember it, type 0 and move right. 2. While the current symbol is not -, remember it, type the previously remembered symbol and move right. 3. Once you see a blank, type the remembered symbol and you are done. Shift Done

3. 1. l A TM for the element distinctness problem Design a TM that decides the language E={#x 1#x 2#…#xn | each xi {0, 1} and xi xj for each i j} See page 135 for a description of such a TM # x 1 # x 2 # x 3 # x 4 # x 5 x 1 # 0 1 x 2 1 # 0 1 x 3 0 # 0 x 4 # 1 1 0 -