CSC 4170 Theory of Computation Regular Expressions Section

CSC 4170 Theory of Computation Regular Expressions Section 1. 3 (also 1. 1, 1. 2)

1. 3. a Union: Regular operations L 1 L 2 = {x | x L 1 or x L 2} {Good, Bad} {Boy, Girl} = {0, 000, …} {1, 111, …} = L = Concatenation: L 1 L 2 = {xy | x L 1 and y L 2} {Good, Bad} {Boy, Girl} = {0, 000, …} {1, 111, …} = L = Star: L* = {x 1…xk | k 0 and each xi L} {Boy, Girl}* = {0, 000, …}* = *=

1. 3. b Regular expressions We say that R is a regular expression (RE) iff R is one of the following: What language is represented by the expression: 1. a, where a is a symbol of the alphabet {a} 2. { } 3. 4. (R 1) (R 2), where R 1 and R 2 are RE The union of the languages represented by R 1 and R 2 The concatenation of the languages represented by R 1 and R 2 The star of the language represented by R 1 5. (R 1) (R 2), where R 1 and R 2 are RE 6. (R 1)*, where R 1 is a RE Conventions: § The symbol is often omitted in RE § Some parentheses can be omitted. The precedence order for the operators is: * (highest), (medium), (lowest)

1. 3. c Regular languages A language is said to be regular iff it can be represented by a regular expression. Language {11} {Boy, Girl, Good, Bad} { , 0, 00, 000, 0000, …} { , 0101, 01010101, …} {x | x = 0 k where k is a multiple of 2 or 3} {x | x is divisible by 8} {x | x MOD 4 = 3} Expression

1. 3. d Exercising reading regular expressions Expression Language (Good Bad)(Boy Girl) (Tom Bob)_is_(good bad) {Name_is_adjective | Name is an uppercase letter followed by zero or more lowercase letters, and adjective is a lowercase letter followed by zero or more lowercase letters} 0*10* (0 1)*101(0 1)* ((0 1))*

1. 3. e Regular languages and DFA-recognizable languages are the same Theorem 1. 54* A language is regular if and only if some NFA (DFA) recognizes it. In other words, a) [The “only if” part] For every regular expression there is an NFA that recognizes exactly the language represented by that expression. b) [The “if” part] For every NFA there is a regular expression that represents exactly the language recognized by that NFA.

1. 3. f Constructing an NFA from a regular expression: Base cases Case of a, where a is a symbol of the alphabet. Case of

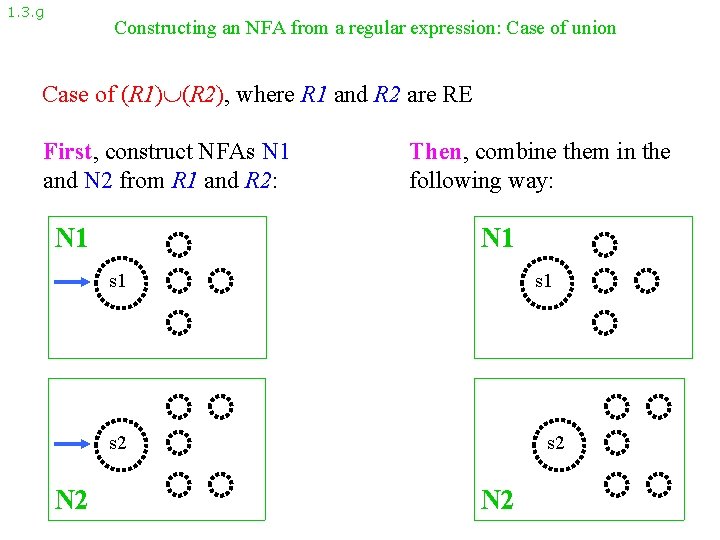
1. 3. g Constructing an NFA from a regular expression: Case of union Case of (R 1) (R 2), where R 1 and R 2 are RE First, construct NFAs N 1 and N 2 from R 1 and R 2: N 1 Then, combine them in the following way: N 1 s 1 s 2 N 2

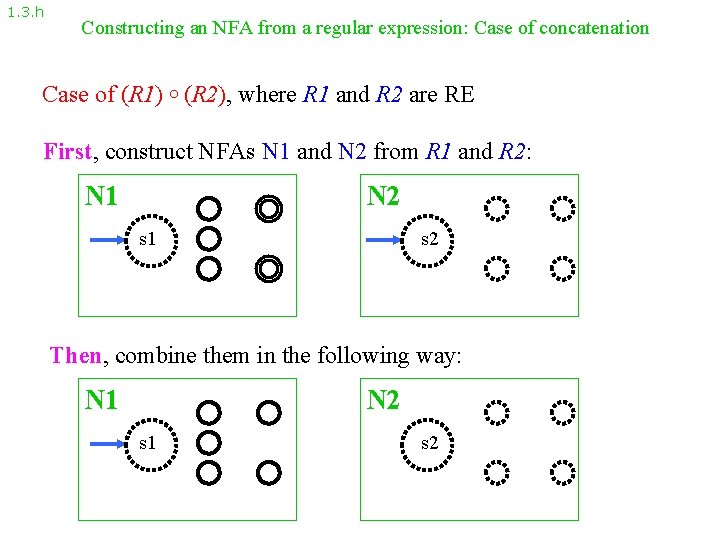
1. 3. h Constructing an NFA from a regular expression: Case of concatenation Case of (R 1) (R 2), where R 1 and R 2 are RE First, construct NFAs N 1 and N 2 from R 1 and R 2: N 1 N 2 s 1 s 2 Then, combine them in the following way: N 1 N 2 s 1 s 2

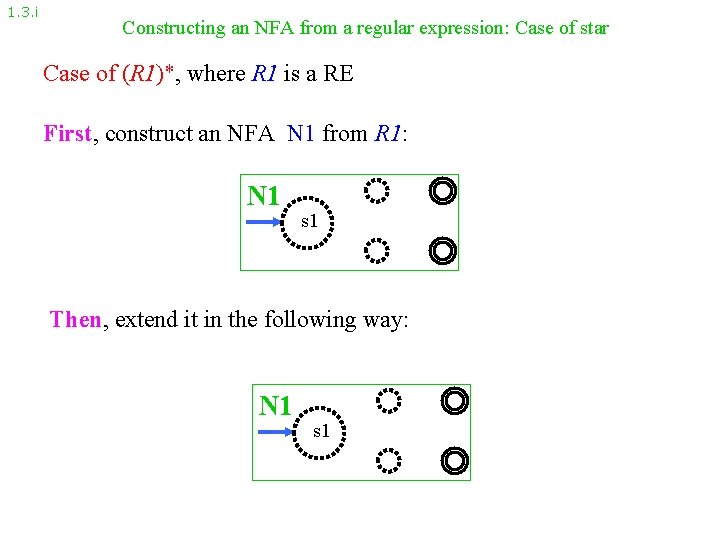
1. 3. i Constructing an NFA from a regular expression: Case of star Case of (R 1)*, where R 1 is a RE First, construct an NFA N 1 from R 1: N 1 s 1 Then, extend it in the following way: N 1 s 1

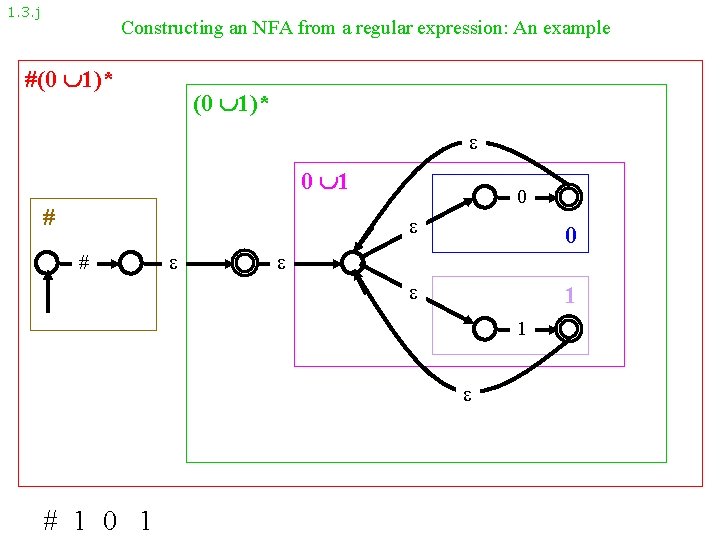
1. 3. j Constructing an NFA from a regular expression: An example #(0 1)* 0 1 # # 0 0 1 1 # 1 0 1

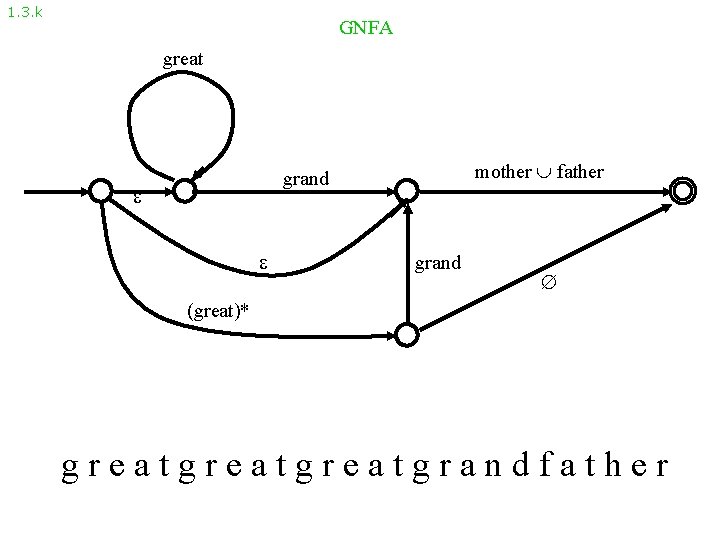
1. 3. k GNFA great mother father grand (great)* greatgreatgrandfather

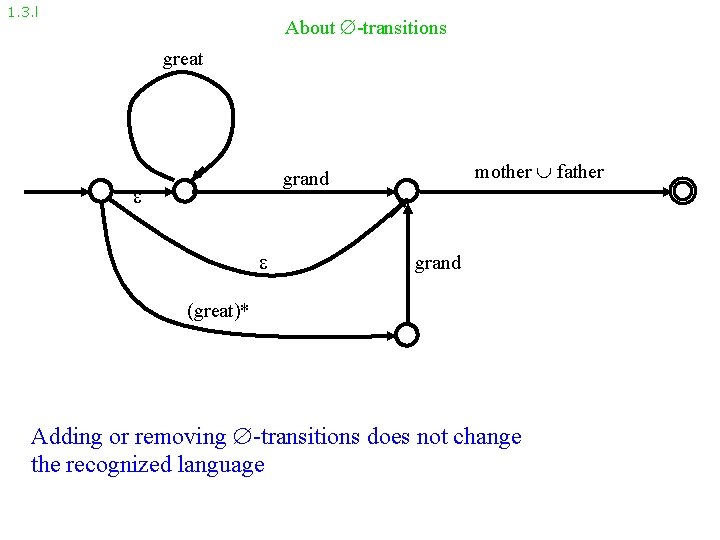
1. 3. l About -transitions great mother father grand (great)* Adding or removing -transitions does not change the recognized language

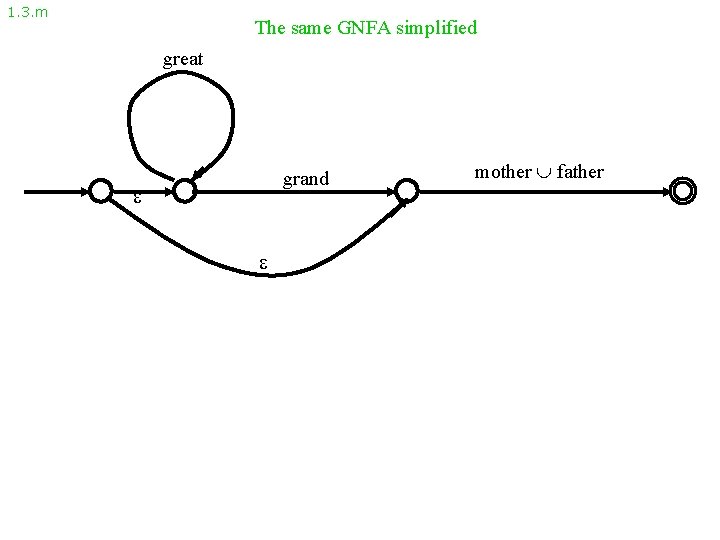
1. 3. m The same GNFA simplified great grand mother father

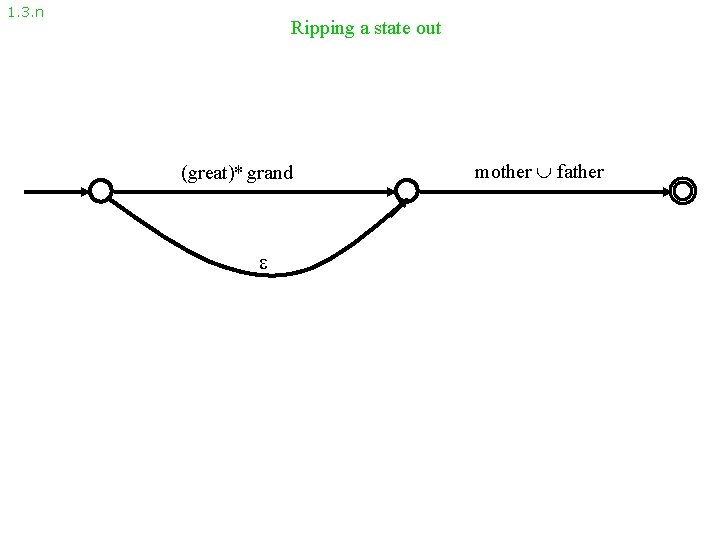
1. 3. n Ripping a state out (great)* grand mother father

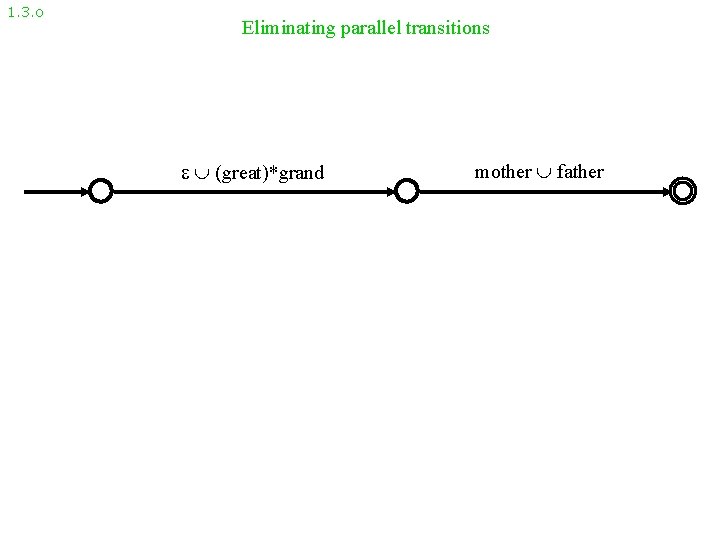
1. 3. o Eliminating parallel transitions (great)*grand mother father

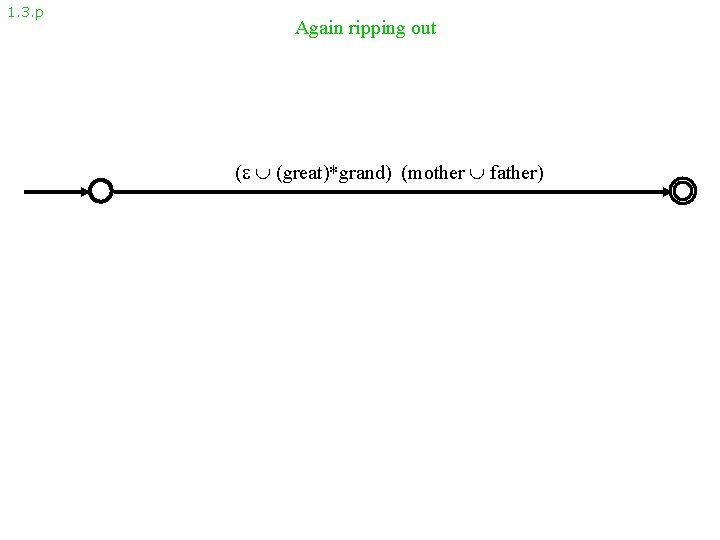
1. 3. p Again ripping out ( (great)*grand) (mother father)

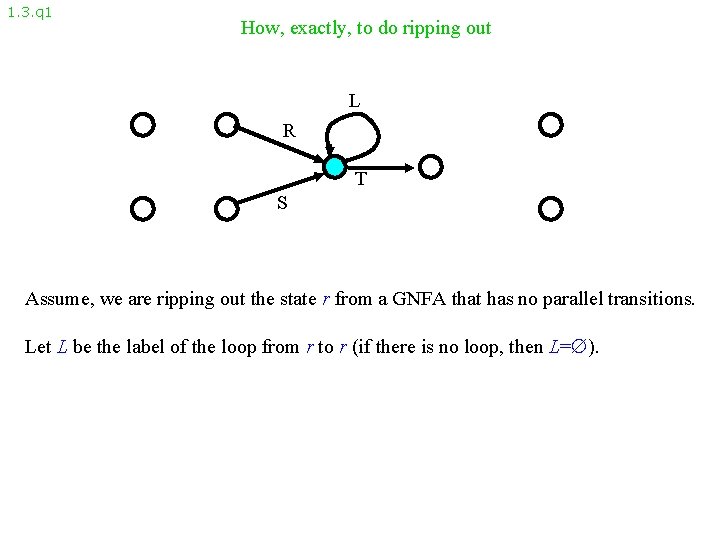
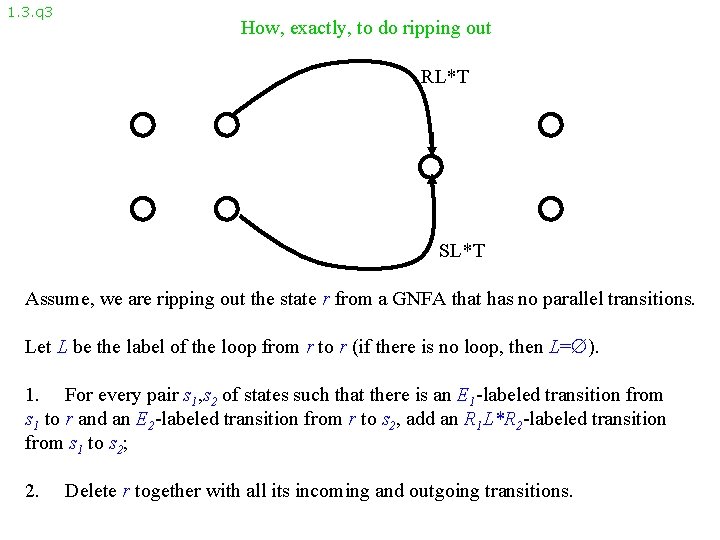
1. 3. q 1 How, exactly, to do ripping out L R T S Assume, we are ripping out the state r from a GNFA that has no parallel transitions. Let L be the label of the loop from r to r (if there is no loop, then L= ).

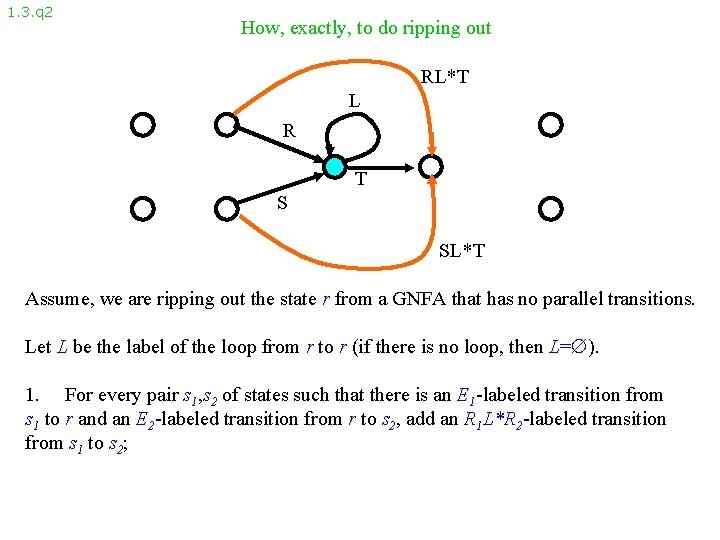
1. 3. q 2 How, exactly, to do ripping out RL*T L R T S SL*T Assume, we are ripping out the state r from a GNFA that has no parallel transitions. Let L be the label of the loop from r to r (if there is no loop, then L= ). 1. For every pair s 1, s 2 of states such that there is an E 1 -labeled transition from s 1 to r and an E 2 -labeled transition from r to s 2, add an R 1 L*R 2 -labeled transition from s 1 to s 2;

1. 3. q 3 How, exactly, to do ripping out RL*T SL*T Assume, we are ripping out the state r from a GNFA that has no parallel transitions. Let L be the label of the loop from r to r (if there is no loop, then L= ). 1. For every pair s 1, s 2 of states such that there is an E 1 -labeled transition from s 1 to r and an E 2 -labeled transition from r to s 2, add an R 1 L*R 2 -labeled transition from s 1 to s 2; 2. Delete r together with all its incoming and outgoing transitions.

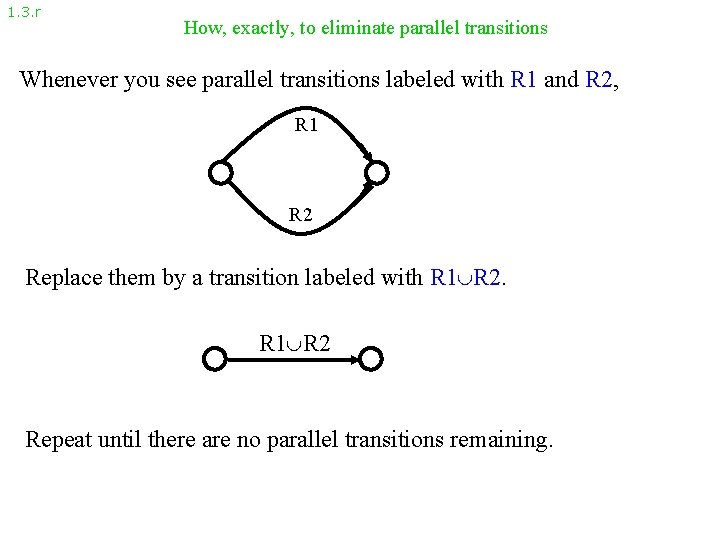
1. 3. r How, exactly, to eliminate parallel transitions Whenever you see parallel transitions labeled with R 1 and R 2, R 1 R 2 Replace them by a transition labeled with R 1 R 2 Repeat until there are no parallel transitions remaining.

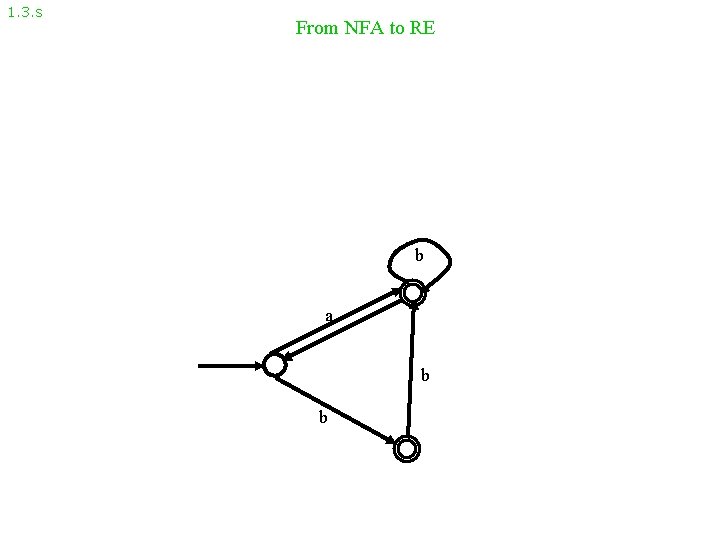
1. 3. s From NFA to RE b a b b

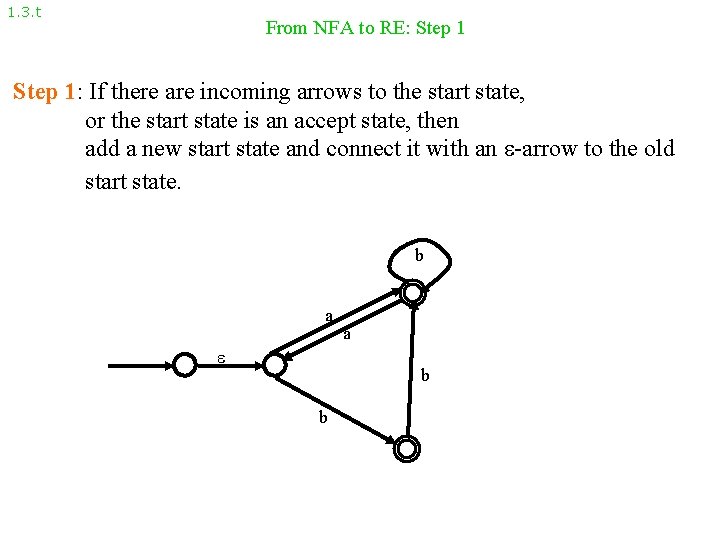
1. 3. t From NFA to RE: Step 1: If there are incoming arrows to the start state, or the start state is an accept state, then add a new start state and connect it with an -arrow to the old start state. b a a b b

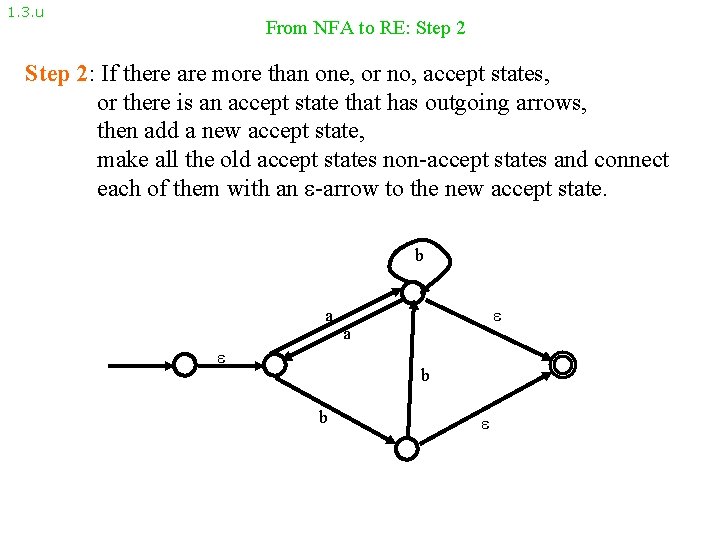
1. 3. u From NFA to RE: Step 2: If there are more than one, or no, accept states, or there is an accept state that has outgoing arrows, then add a new accept state, make all the old accept states non-accept states and connect each of them with an -arrow to the new accept state. b a a b b

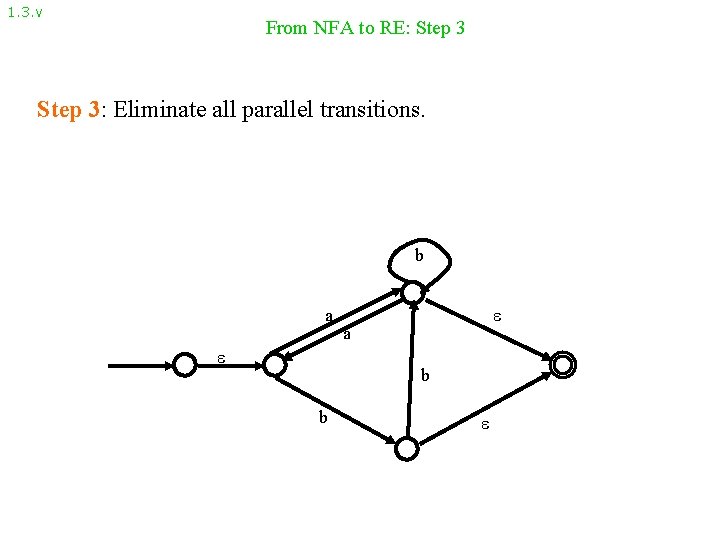
1. 3. v From NFA to RE: Step 3: Eliminate all parallel transitions. b a a b b

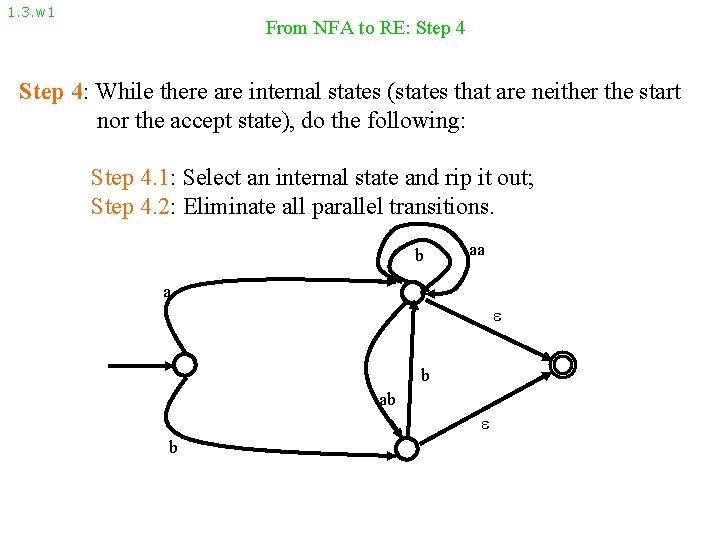
1. 3. w 1 From NFA to RE: Step 4: While there are internal states (states that are neither the start nor the accept state), do the following: Step 4. 1: Select an internal state and rip it out; Step 4. 2: Eliminate all parallel transitions. b aa a b ab b

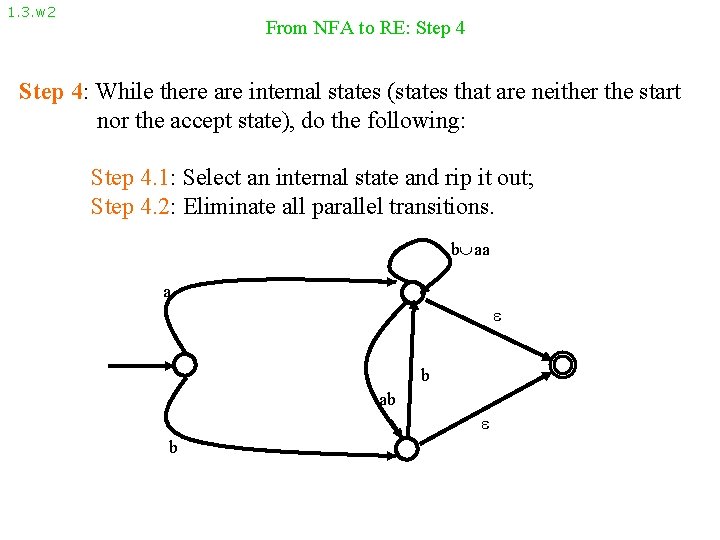
1. 3. w 2 From NFA to RE: Step 4: While there are internal states (states that are neither the start nor the accept state), do the following: Step 4. 1: Select an internal state and rip it out; Step 4. 2: Eliminate all parallel transitions. b aa a b ab b

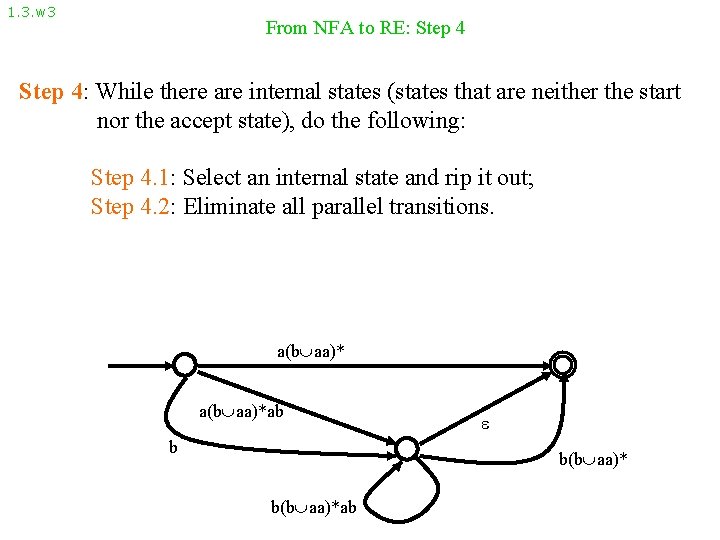
1. 3. w 3 From NFA to RE: Step 4: While there are internal states (states that are neither the start nor the accept state), do the following: Step 4. 1: Select an internal state and rip it out; Step 4. 2: Eliminate all parallel transitions. a(b aa)*ab b b(b aa)*ab

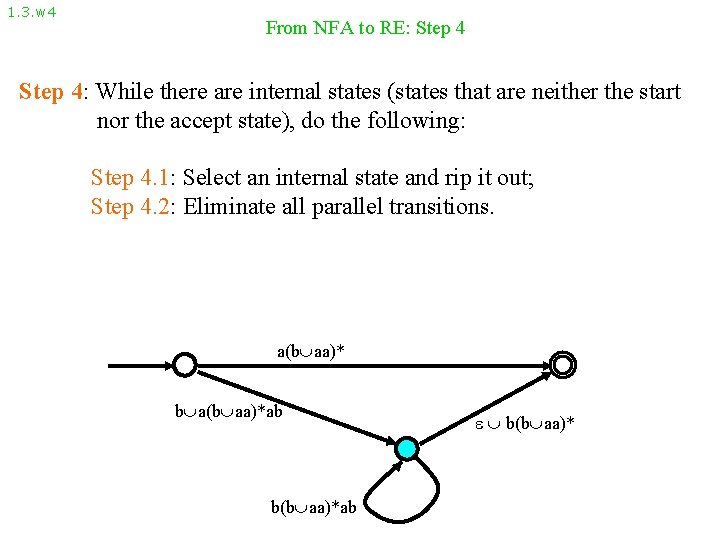
1. 3. w 4 From NFA to RE: Step 4: While there are internal states (states that are neither the start nor the accept state), do the following: Step 4. 1: Select an internal state and rip it out; Step 4. 2: Eliminate all parallel transitions. a(b aa)* b a(b aa)*ab b(b aa)*

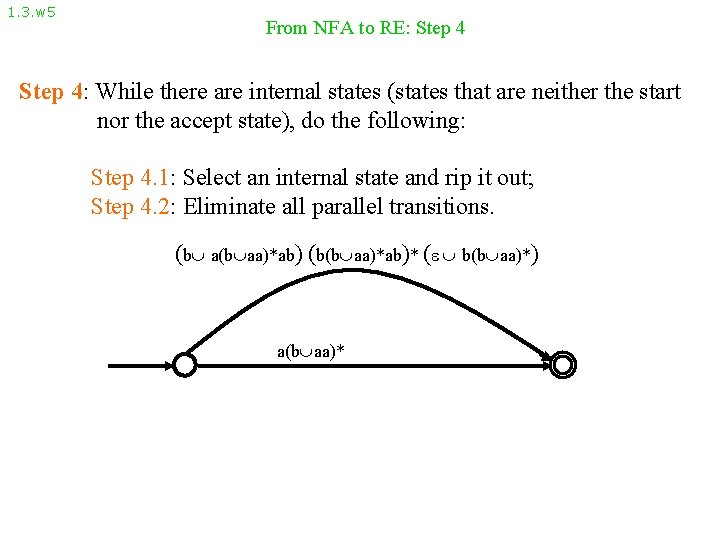
1. 3. w 5 From NFA to RE: Step 4: While there are internal states (states that are neither the start nor the accept state), do the following: Step 4. 1: Select an internal state and rip it out; Step 4. 2: Eliminate all parallel transitions. (b aa)*ab) (b(b aa)*ab)* ( b(b aa)*) a(b aa)*

1. 3. w 6 From NFA to RE: Step 4: While there are internal states (states that are neither the start nor the accept state), do the following: Step 4. 1: Select an internal state and rip it out; Step 4. 2: Eliminate all parallel transitions. ((b aa)*ab) (b(b aa)*ab)* ( b(b aa)*) (a(b aa)*)

1. 3. x From NFA to RE: Step 5: Return the label of the only remaining arrow (if there is no arrow, return ). ((b a(b aa)*ab) (b(b aa)*ab)* ( b(b aa)*) (a(b aa)*) Claim: The resulting RE represents exactly the language recognized by the original NFA. This completes the proof of Theorem 1. 54.