CSC 4170 Theory of Computation Nonregular Languages Section





- Slides: 6

CSC 4170 Theory of Computation Nonregular Languages Section 1. 4

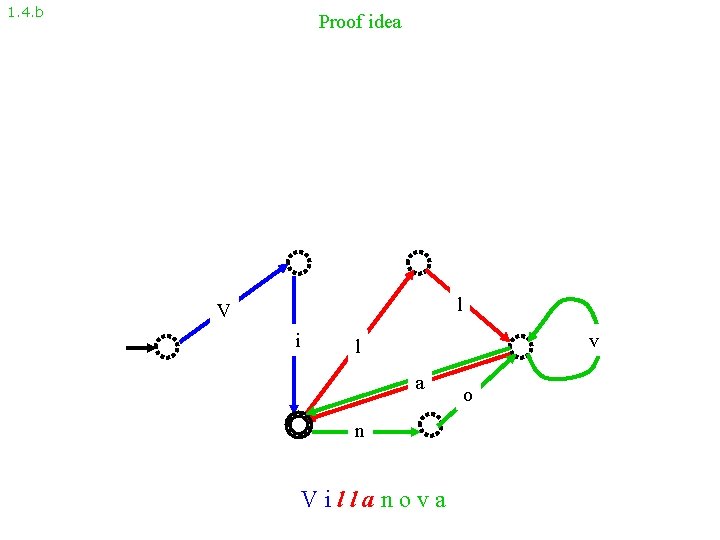
1. 4. a Pumping Lemma (preliminary version): Suppose L is the language recognized by a DFA with p states, and w is a string in L of length at least p. Then w may be divided into three parts, w = xyz, so that: 1. For each i 0, xyiz L; 2. |y| > 0; 3. |xy| p. Example: Suppose a DFA with 6 states accepts Villanova. Then Villanova = xyz, e. g. , with x = Vi, y = lla, z = nova, Villanova so that the DFA also accepts Vinova (xy 0 z) We also have: |lla| > 0, |Villa| 6. Villanova Villallallanova Villallanova … (xy 1 z) (xy 2 z) (xy 3 z) (xy 4 z)

1. 4. b Proof idea l V i v l a n Villanova o

1. 4. c An equivalent formulation of the pumping lemma Pumping Lemma (Theorem 1. 70): Suppose L is a regular language. Then there is a number p, called the pumping length, such that any string w from L of length at least p can be divided into three parts, w = xyz, so that: 1. For each i 0, xyiz L; 2. |y| > 0; 3. |xy| p. Proof: Suppose L is a regular language. Then we know that there must be a DFA recognizing L. Take the pumping length p to be the number of states of this DFA. The rest of theorem is then a repetition of the previous formulation of the pumping lemma.

1. 4. d Using the pumping lemma for proving nonregularity: Example 1. 73: Show the nonregularity of B = {0 n 1 n | n 0} Proof by contradiction: Assume B is regular. Let then p be its pumping length. Select w B with |w| p. By the pumping lemma, w=xyz and y can be pumped, so that we must also have xyyz B. Case 1: y only has 0 s. But then xyyz has more 0 s than 1 s and B. Case 2: y only has 1 s. But then xyyz has more 1 s than 0 s and B. Case 3: y has both 0 s and 1 s. But then xyyz has a 1 followed by a 0 and B. The assumption that B is regular took us to a contradiction. Hence the assumption was wrong, i. e. B is not regular.

1. 4. e Using the pumping lemma for proving nonregularity: Example 2 Example 1. 75: Show the nonregularity of F = { ww | w {0, 1}* } Proof by contradiction: Assume F is regular. Let then p be its pumping length. Observe that 0 p 1 F. By the pumping lemma, 0 p 1 =xyz and y can be pumped. By Condition 3, |xy| p. Therefore, y is entirely in the first 0 p. Pumping y would produce a string that has only 0 s is the first half, and two 1 s in the second half. Obviously this string cannot be in F, which contradicts with the pumping lemma. The assumption that F is regular took us to a contradiction. Hence the assumption was wrong, i. e. F is not regular.