CSC 382 Computer Security Classical Cryptography CSC 382

CSC 382: Computer Security Classical Cryptography CSC 382: Computer Security 1

Overview 1. 2. 3. 4. Modular Arithmetic Review What is Cryptography? Transposition Ciphers Substition Ciphers 1. Cæsar cipher 2. Vigènere cipher 5. Cryptanalysis: frequency analysis 6. Block Ciphers 7. DES CSC 382: Computer Security 2

Modular Arithmetic Congruence – a = b (mod N) iff a = b + kn – Equivalently, a = b (mod N) iff N / (a – b) – ex: 37=27 mod 10 b is the residue of a, modulo N – Ints 0. . N-1 are complete set of residues mod N CSC 382: Computer Security 3

Laws of Modular Arithmetic 1. 2. 3. 4. (a + b) mod N = (a mod N + b mod N) mod N (a - b) mod N = (a mod N - b mod N) mod N ab mod N = (a mod N)(b mod N) mod N a(b+c) mod N = ((ab mod N)+(ac mod N)) mod N CSC 382: Computer Security 4

What is Cryptography? Cryptography: The art and science of keeping messages secure. Cryptanalysis: the art and science of decrypting messages. Cryptology: cryptography + cryptanalysis CSC 382: Computer Security 5

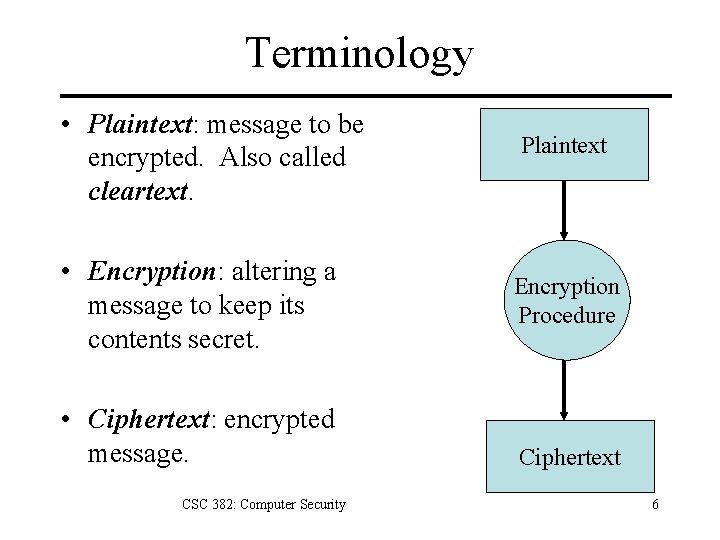
Terminology • Plaintext: message to be encrypted. Also called cleartext. • Encryption: altering a message to keep its contents secret. • Ciphertext: encrypted message. CSC 382: Computer Security Plaintext Encryption Procedure Ciphertext 6

History of Cryptography Egyptian hieroglyphics ~ 2000 B. C. E. – Cryptic tomb enscriptions for regality. Spartan skytale cipher ~ 500 B. C. E. – Wrapped thin sheet of papyrus around staff. – Messages written down length of staff. – Decrypted by wrapped around = diameter staff. Cæsar cipher ~ 50 B. C. E. – Simple alphabetic substitution cipher. al-Kindi ~ 850 C. E. – Cryptanalysis using letter frequencies. CSC 382: Computer Security 7

History of Cryptography Alberti’s polyalphabetic cipher 1467 Decryption of Zimmerman telegram 1917 – Leads US into World War I Japanese Purple Machine cracked 1937 – US breaks rotor machine for highest secrets. German Enigma machine cracked 1933 -45 – Initially broken by Polish mathematician Rejewski – Variants broken at Bletchley Park in UK – Colossus, world’s 1 st electronic computer. CSC 382: Computer Security 8

Cryptosystem Formal Definition 5 -tuple (E, D, M, K, C) – M set of plaintexts – K set of keys – C set of ciphertexts – E set of encryption functions e: M K C – D set of decryption functions d: C K M CSC 382: Computer Security 9

Example: Cæsar cipher Letter shifting cipher (A=>D, B=>E, C=>F, …) 5 -tuple – M = { all sequences of letters } – K = { i | i is an integer and 0 ≤ i ≤ 25 } – E = { Ek | k K and for all letters m, Ek(m) = (m + k) mod 26 } – D = { Dk | k K and for all letters c, Dk(c) = (26 + c – k) mod 26 } – C=M History: Cæsar’s key was 3. CSC 382: Computer Security 10

Example: Cæsar cipher • Plaintext is HELLO WORLD • Change each letter to the third letter following it (X goes to A, Y to B, Z to C) – Key is 3, usually written as letter ‘D’ • Ciphertext is KHOOR ZRUOG CSC 382: Computer Security 11

A Transposition Cipher Rearrange letters in plaintext. Example: Rail-Fence Cipher – Plaintext is HELLO WORLD – Rearrange as H L O O L E L W R D – Ciphertext is HLOOL ELWRD CSC 382: Computer Security 12

Cryptosystem Security Dependencies 1. Quality of shared encryption algorithm E 2. Secrecy of key K CSC 382: Computer Security 13

Cryptanalysis Goals – Decrypt a given message. – Recover encryption key. Adversarial models vary based on – Type of information available to adversary – Interaction with cryptosystem. CSC 382: Computer Security 14

Cryptanalysis Adversarial Models 1. ciphertext only: adversary has only ciphertext; goal is to find plaintext, possibly key. 2. known plaintext: adversary has ciphertext, corresponding plaintext; goal is to find key. 3. chosen plaintext: adversary may supply plaintexts and obtain corresponding ciphertext; goal is to find key. CSC 382: Computer Security 15

Classical Cryptography Sender & receiver share common key – Keys may be the same, or trivial to derive from one another. – Sometimes called symmetric cryptography. CSC 382: Computer Security 16

Substitution Ciphers Substitute plaintext chars for ciphered chars. – Simple: Always use same substitution function. – Polyalphabetic: Use different substitution functions based on position in message. CSC 382: Computer Security 17

Cryptanalysis of Cæsar Cipher Exhaustive search – If the key space is small enough, try all possible keys until you find the right one. – Cæsar cipher has 26 possible keys. CSC 382: Computer Security 18

General Simple Substitution Cipher Key Space: All permutations of alphabet. Encryption: – Replace each plaintext letter x with K(x) Decryption: – Replace each ciphertext letter y with K-1(y) Example: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z K= F U B A R D H G J I L K N M P O S Q Z W X Y V T C E CRYPTO BQCOWP CSC 382: Computer Security 19

General Substitution Cryptanalysis Exhaustive search impossible – Key space size is 26! =~ 4 x 1026 – Historically thought to be unbreakable. – Yet people solve them as newspaper puzzles every day… Solution: frequency analysis. Lesson: A large key space is necessary but not sufficient for security of a cryptosystem. CSC 382: Computer Security 20

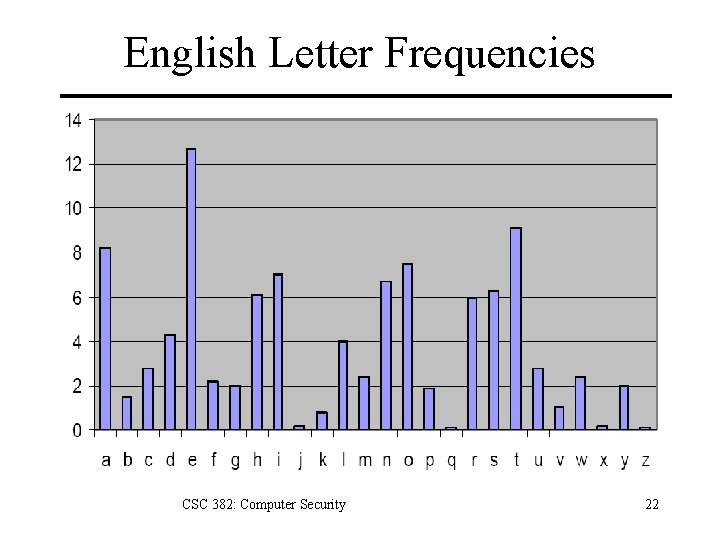
Cryptanalysis: Frequency Analysis Languages have different frequencies of – letters – digrams (groups of 2 letters) – trigrams (groups of 3 letters) – etc. Simple substitution ciphers preserve frequency distributions. CSC 382: Computer Security 21

English Letter Frequencies CSC 382: Computer Security 22

Additional Frequency Features 1. Digram frequencies – Common digraphs: EN, RE, ER, NT, TH 2. Trigram frequencies – Common trigrams: THE, ING, THA, ENT 3. Vowels other than E rarely followed by another vowel. 4. The letter Q is followed only by U. 5. Many others. CSC 382: Computer Security 23

Countering Frequency Analysis Nulls – Insert additional symbols (numbers) which have no meaning in random places. Idiosyncratic spellings – Hacker speak: www. google. com/intl/xx-hacker Homophonic substitution – Each letter has multiple substitutions. These techniques increase difficulty of frequency analysis but don’t make it impossible. CSC 382: Computer Security 24

Countering Frequency Analysis Primary weakness of simple substition: – Each ciphertext letter corresponds to only one letter of plaintext. Solution: polyalphabetic substitution – Use multiple cipher alphabets. – Switch between cipher alphabets from character to character in the plaintext. CSC 382: Computer Security 25

Letter Frequency Distributions CSC 382: Computer Security 26

Vigènere Cipher Use phrase instead of letter as key. Example: – Message THE BOY HAS THE BALL – Key VIG – Encipher using Cæsar cipher for each letter: key VIGVIGVIGV plain THEBOYHASTHEBALL cipher OPKWWECIYOPKWIRG Key space size is 26 m. CSC 382: Computer Security 27

Relevant Parts of Tableau A B E H L O S T Y G G H L N R U Y Z E I I J M P T W A B H V V W Z C G J N O T CSC 382: Computer Security Tableau shown has relevant rows, columns only. Example encipherments: 1. 2. key V, letter T: follow V column down to T row (giving “O”) Key I, letter H: follow I column down to H row (giving “P”) 28

Useful Terms period: length of key – In earlier example, period is 3 tableau: table used to encipher and decipher – Vigènere cipher has key letters on top, plaintext letters on the left. CSC 382: Computer Security 29

Simple Attacks 1. Chosen Plaintext – Choose plaintext of all a’s. – If long enough, it will be encrypted to the key. 2. Dictionary Attack – Guess key from dictionary and try decryption. 3. Brute Force – Try every possible key in turn. – Is there a ciphertext only attack that’s faster? CSC 382: Computer Security 30

Vigènere Cryptanalysis 1. Find key length (period). 2. Break message into n parts, each part being enciphered using the same key letter. 3. Use frequency analysis to solve resulting simple substition ciphers. key VIGVIGVIGV plain THEBOYHASTHEBALL cipher OPKWWECIYOPKWIRG CSC 382: Computer Security 31

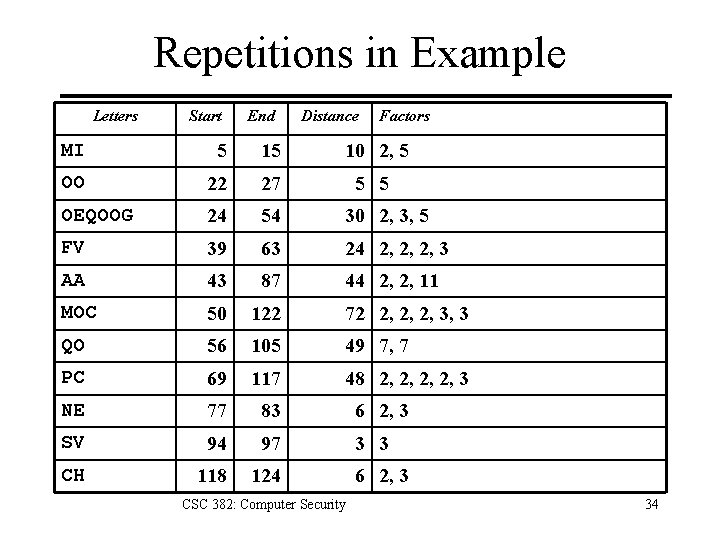
Kaskski Test • Conjunction of key repetition with repeated portion of plaintext produces repeated ciphertext. • Example: key VIGVIGVIGV plain THEBOYHASTHEBALL cipher OPKWWECIYOPKWIRG Key and plaintext line up over the repetitions. • Distance between reptitions is 9 – Repeated phrase “OPK” at 1 st and 10 th positions. – Period is a multiple of 9 (1, 3 or 9. ) CSC 382: Computer Security 32

Example Vigènere Ciphertext ADQYS EQOOG MOCIO HSNEW HCEUT HIUIX MIUSB IFBAG EQOOG VECNE QOIOF OXKKT KAUMF BMBFV DLAAV MEGJS CSC 382: Computer Security MIBHK VVTAA ZGGWP RWKXS WTPCH IZOOO CIDTW CIEKQ VNSVP AJMOC 33

Repetitions in Example Letters Start End Distance Factors MI 5 15 10 2, 5 OO 22 27 5 5 OEQOOG 24 54 30 2, 3, 5 FV 39 63 24 2, 2, 2, 3 AA 43 87 44 2, 2, 11 MOC 50 122 72 2, 2, 2, 3, 3 QO 56 105 49 7, 7 PC 69 117 48 2, 2, 3 NE 77 83 6 2, 3 SV 94 97 3 3 CH 118 124 CSC 382: Computer Security 6 2, 3 34

Estimate of Period • OEQOOG is probably not a coincidence – Two character repetitions may be chance. – Period may be 1, 2, 3, 5, 6, 10, 15, or 30 • Most others (7/10) have 2 in their factors • Almost as many (6/10) have 3 in their factors. • Begin with period of 2 3 = 6. CSC 382: Computer Security 35

Letter Coincidence • Coincidence: Picking two letters at random from a message that are identical. • Probability of picking two a’s – Let there be n letters in the ciphertext. – Let there be na a’s in the ciphertext. – The probability of selecting two a’s at random CSC 382: Computer Security 36

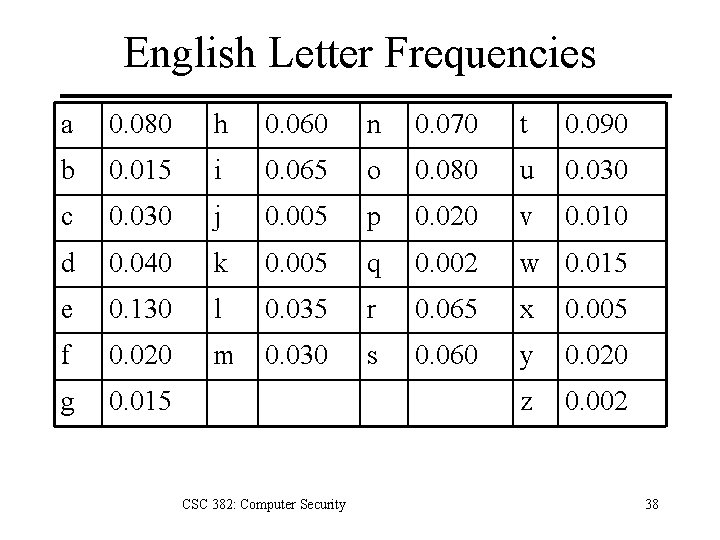
Index of Coincidence Probability of chosing two identical letters Coincidence probabilities for two letters: – English plaintext: 0. 0667 – Random English letters: 1/26 @ 0. 0385 CSC 382: Computer Security 37

English Letter Frequencies a 0. 080 h 0. 060 n 0. 070 t 0. 090 b 0. 015 i 0. 065 o 0. 080 u 0. 030 c 0. 030 j 0. 005 p 0. 020 v 0. 010 d 0. 040 k 0. 005 q 0. 002 w 0. 015 e 0. 130 l 0. 035 r 0. 065 x 0. 005 f 0. 020 m 0. 030 s 0. 060 y 0. 020 g 0. 015 z 0. 002 CSC 382: Computer Security 38

Coincidence Counting Simple Language: f(A)=0. 75, f(B)=0. 25 Simple Cipher: Swap A’s and B’s Plaintext AA BB AB BA . 5625. 0625. 1875 CSC 382: Computer Security Plaintext/Ciphertext AA BB AB BA . 1875. 5625. 0625 39

Friedman Test Expected IC by period Expected IC – Random: 0. 0385 – Plaintext: 0. 0667 – 2: 0. 052 – 3: 0. 047 – 4: 0. 045 – 5: 0. 044 – 10: 0. 041 Index of Coincidence Shorter Key 0. 0385 Longer Key CSC 382: Computer Security 0. 0667 40

Compute I. C. for Example For our ciphertext, IC = 0. 043 – Indicates a key of slightly more than 5. – A statistical measure, so it can be in error, but it agrees with the previous estimate (6). If the key has m characters, then every mth character is enciphered with the same shift. – The string of letters won’t be recognizable. – But its letter frequencies should be the same as English as it’s a monoalphabetic ciphertext. CSC 382: Computer Security 41

Splitting Into Alphabets Divide cipher into 6 (period) alphabets. Alphabet AIKHOIATTOBGEEERNEOSAI DUKKEFUAWEMGKWDWSUFWJU QSTIQBMAMQBWQVLKVTMTMI YBMZOAFCOOFPHEAXPQEPOX SOIOOGVICOVCSVASHOGCC MXBOGKVDIGZINNVVCIJHH IC 0. 069 0. 078 0. 056 0. 124 0. 043 IC indicates single alphabet, except #4 and #6. CSC 382: Computer Security 42

Frequency Examination ABCDEFGHIJKLMNOPQRSTUVWXYZ 1 31004011301001300112000000 2 10022210013010000010404000 3 12000000201140004013021000 4 21102201000010431000000211 5 10500021200000500030020000 6 01110022311012100000030101 HMMMHMMHHMMMMHHMLHHHMLLLLL Unshifted frequencies (H high, M medium, L low) CSC 382: Computer Security 43

Begin Decryption • • First matches characteristics of unshifted alphabet Third matches if I shifted to A Sixth matches if V shifted to A Substitute into ciphertext (bold are substitutions) ADIYS RIUKB OCKKL MIGHK AZOTO EIOOL IFTAG PAUEF VATAS CIITW EOCNO EIOOL BMTFV EGGOP CNEKI HSSEW NECSE DDAAA RWCXS ANSNP HHEUL QONOF EEGOS WLPCM AJEOC MIUAX CSC 382: Computer Security 44

Look For Clues AJE in last line suggests “are”, meaning second alphabet maps A into S: ALIYS MIOOL EOCNO HSSEE HHECL MICAX RICKB INTAG MIOOL NECSE QONON OCKSL PACEF BUTFV LDAAA EEGOS CSC 382: Computer Security MIGHS VATIS EGOOP RECXS ELPCM AZOTO CIITE CNESI ANANP AREOC 45

Next Alphabet MICAX in last line suggests “mical” (a common ending for an adjective), meaning fourth alphabet maps O into A: ALIMS MICOL ECCNO VSSEE HHECL MICAL RICKP INTOG MICOL NSCSE EONON OCKSL PACET BUTTV LDOAA ESGOS CSC 382: Computer Security AIGHS VATIS EGOOD RECLS ELDCM ANOTO QIITE CNESI ANAND ARECC 46

Got It! QI means that U maps into I, as Q is always followed by U: ALIME MICAL ECONO VESEE THECL MICAL RICKP INTOS MICAL NSOSE EANON ACKSL PACET BUTTH LDOMA ESSOS CSC 382: Computer Security AUGHS HATIS EGOOD RECLE ELDOM ANATO QUITE ONESI ANAND ARECO 47

Countering Frequency Analaysis • Observation: If Vigènere key is very long, frequency analysis won’t work. • Problem: Long keys are hard to remember. • Solution: Use multiple encryptions. – Encrypting with a key m and key n is same as encryption by key whose length is least common multiple of m and n. – If m and n are relatively prime, then the least common multiple is mn. CSC 382: Computer Security 48

Rotor Machines Use multiple rounds of Vigènere substitution. – Machine contains multiple cylinders. – Each cylinder has 26 states (ciphers). – Cylinders rotate to change states on different schedules. – m-cylinder machine has 26 m substitution ciphers. CSC 382: Computer Security 49

Enigma Machine • 3 rotors: 17576 substitutions. • 3 rotors can be used in any order: 6 combinations. • Plug board: 6 pairs of letters can be swapped. • Total keys ~ 1016 CSC 382: Computer Security 50

Perfect Security: The One-Time Pad • A Vigenère cipher with a random key at least as long as the message. • Provably unbreakable. • Example ciphertext: DXQR. • Equally likely to correspond to – plaintext DOIT (key AJIY) – plaintext DONT (key AJDY) – and any other 4 letters. CSC 382: Computer Security 51

One-Time Pad • Warning: keys must be random, or you can attack the cipher by trying to regenerate the key. • Approximations, such as using computer pseudorandom number generators to generate keys, are not random. CSC 382: Computer Security 52

Block Ciphers • Encrypt groups (blocks) of chars at once. • Improvement over single char substitution – Cryptanalysis must use digraph frequencies for two-char blocks. – Longer blocks are more difficult to analyze. – Modern ciphers are block ciphers. • Example: Playfair Cipher, 1854 CSC 382: Computer Security 53

Playfair Cipher Create 5 x 5 table – Fill in spaces with letters of key, dropping duplicate letters. – Fill remaining spaces with unused letters of alphabet in order • Drop Q … or • I=J CSC 382: Computer Security P I|J B K T L R C N U A E D O V Y X G Q W F M H S Z 54

Playfair Cipher Encryption Algorithm 1. If letters of pair are identical (or only one letter remains), add an “X” after first letter. 2. If two letters are in same row or column, replace them with the succeeding letters. 3. Otherwise, two letters form a rectangle, and we replace them with letters on the same row respectively at the other pair of corners. CSC 382: Computer Security 55

Playfair Cipher Example Plaintext is HELLO WORLD – Pair HE is rectangle, replace with DM – Pair LX (X inserted) is rectangle, YR – Pair LO is rectangle, replace with AN – Pair WO is rectangle, replace with VQ – Pair RL is in column, replace with CR – Pair DX is rectangle, replace with GE Ciphertext is DMYRANVQCRGE CSC 382: Computer Security 56

Transposition Cipher Cryptanalysis Anagramming – If • 1 -gram frequencies match English frequencies, • but other n-gram frequencies do not, – then, message likely ciphered via transposition. – Rearrange letters to form n-grams with highest frequencies. CSC 382: Computer Security 57

Cryptanalysis Example Ciphertext: HLOOLELWRD Frequencies of 2 -grams beginning with H – HE 0. 0305 – HO 0. 0043 – HL, HW, HR, HD < 0. 0010 Frequencies of 2 -grams ending in H – WH 0. 0026 – EH, LH, OH, RH, DH ≤ 0. 0002 Implies E follows H CSC 382: Computer Security 58

Cryptanalysis Example Arrange so the H and E are adjacent HE LL OW OR LD Read across, then down, to recover plaintext. CSC 382: Computer Security 59

Shannon Criteria 1. Kerchoff’s Principle – The only secret should be the key. – Cipher should be secure if mechanism known but not the key. 2. Incorporate both confusion + diffusion – Confusion: hide local patterns of language. – Diffusion: hide large-scale patterns by mixing different parts of plaintext. CSC 382: Computer Security 60

SP-Networks Combine Substitution+Permutation (transposition) – Confusion: adding unknown key values will confuse attacker about value of plaintext symbol. – Diffusion: Transposing text to ensure nothing is left in its original position. Designing for Security – Block Size – Number of Rounds • Each input bit is XOR of several output bits from previous round. – Choice of S-boxes CSC 382: Computer Security 61

Overview of the DES 1. Block cipher: encrypts blocks of 64 bits – 56 -bit key + 8 parity bits 2. Product cipher – substitution + transposition 3. 16 rounds (iterations) of encryption – – Round key generated from user key Each round is a Feistel network. CSC 382: Computer Security 62

Feistel Network • Start: string of 2 n bits • Group into two halves, L and R, each a vector of n bits. • Let f be any function that – Accepts inputs of n bits. – Produces output of n bits. • Feistel network Ff is • Ff is its own inverse CSC 382: Computer Security 63

Generation of Round Keys Drop parity bits, reducing effective key size to 56 bits. Permute and extract 48 bits for round key. CSC 382: Computer Security 64

Encipherment Split 64 -bit block L 0=init left half R 0=init right half Encrypt with f=round fn K 1=round 1 key Join L + R halves L 16=round 16 left half R 16=round 16 right half CSC 382: Computer Security 65

The f Function Each round has effect: Li = Ri-1 Ri = Li-1 + f(Ri-1, Ki) CSC 382: Computer Security 66

Controversy Considered too weak – Diffie, Hellman said in a few years technology would allow DES to be broken in days (1976). • EFF built “Deep Crack” in 1998 for $100, 000. • Brute forced DES in 56 hours. – Design decisions not public • NSA involved in weakening cipher. • 128 -bit key reduced to 56 bits. • S-boxes may have backdoors. CSC 382: Computer Security 67

Undesirable Properties • 4 weak keys – They are their own inverses. • 12 semi-weak keys – Each has another semi-weak key as inverse. • Complementation property – DESk(m) = c DESk´(m´) = c´ • S-boxes exhibit irregular properties – Distribution of odd, even numbers non-random. – Outputs of fourth box depends on input to third box. CSC 382: Computer Security 68

Differential Cryptanalysis • A chosen ciphertext attack – – Biham and Shamir (1990) Examines pairs of plaintext with particular diffs. Requires 247 plaintext, ciphertext pairs. Only 214 pairs required with 8 round DES. • Revealed several properties – S-box designed to resist differential cryptanalysis. – IBM revealed knowledge of technique at design time. • Linear cryptanalysis improves result – Linear approximation of DES. – Requires 243 plaintext, ciphertext pairs. – DES not designed to resist this technique. CSC 382: Computer Security 69

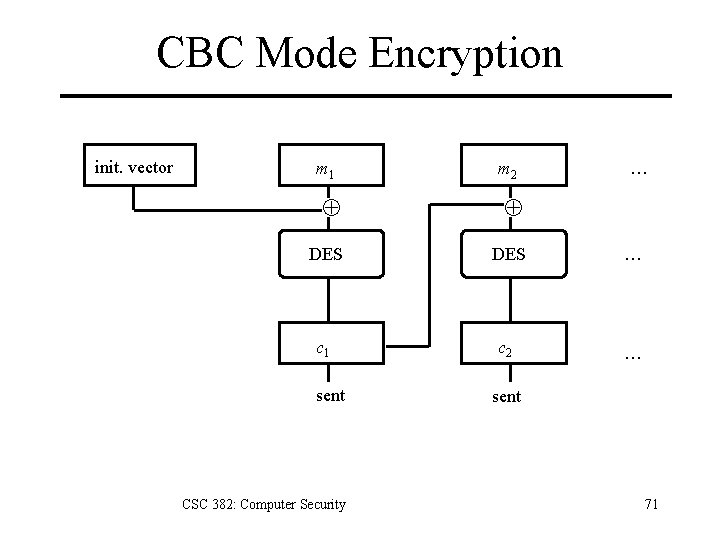
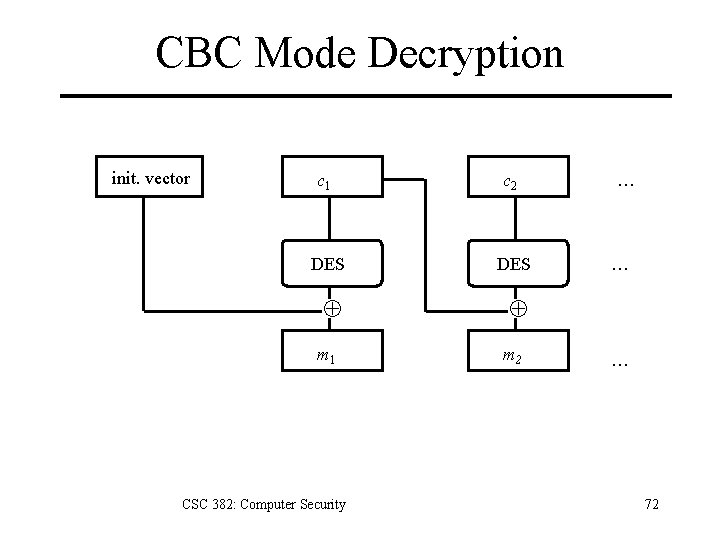
DES Modes • Electronic Code Book Mode (ECB) – Encipher each block independently. Insecure. • Cipher Block Chaining Mode (CBC) – XOR each block with previous ciphertext block. – Requires an initialization vector for the first one. • Triple DES: Encrypt-Decrypt-Encrypt Mode (3 keys: k, k´´) – c = DESk(DESk´– 1(DESk’’(m))) – Double-encryption vulnerable to meet-in-middle attack, reducing difficulty from 2112 to 257. CSC 382: Computer Security 70

CBC Mode Encryption init. vector m 1 m 2 … DES … c 1 c 2 … sent CSC 382: Computer Security sent 71

CBC Mode Decryption init. vector c 1 c 2 DES m 1 CSC 382: Computer Security m 2 … … … 72

Self-Healing Property • Plaintext “heals” after 2 blocks. – i. e. , if ciphertext altered, error propagated 2 blocks. • Initial message – 3231343336353837 • Received as (underlined 4 c should be 4 b) – ef 7 c 4 cb 2 b 4 ce 6 f 3 b f 6266 e 3 a 97 af 0 e 2 c 746 ab 9 a 6308 f 4256 33 e 60 b 451 b 09603 d • Which decrypts to – efca 61 e 19 f 4836 f 1 3231333336353837 3231343336353837 CSC 382: Computer Security 73

Current Status of DES • Design for computer system, associated software that could break any DES-enciphered message in a few days published in 1998. • Several challenges to break DES messages solved using distributed computing. • NIST selected Rijndael as Advanced Encryption Standard, successor to DES. – 128 -bit block product cipher. – Designed to withstand attacks that succeeded on DES. – Keys: 128, 192, or 256 bits. CSC 382: Computer Security 74

Key Points 1. Cryptography is the art of securing messages. 2. Types of ciphers 1. Substitition 2. Transposition (permutation) 3. Product 3. Cryptanalysis 1. Language features can be used to break ciphers. 2. Frequency analysis: Kaski test, Index of Coincidence. 4. Block ciphers 1. DES CSC 382: Computer Security 75

References 1. 2. 3. 4. 5. 6. 7. 8. 9. Matt Bishop, Introduction to Computer Security, Addison-Wesley, 2005. Paul Garrett, Making, Breaking Codes: An Introduction to Cryptology, Prentice Hall, 2001. David Kahn, The Codebreakers, Mac. Millan, 1967. Wenbo Mao, Modern Cryptography: Theory and Practice, Prentice Hall, 2004. Alfred J. Menezes, Paul C. van Oorschot and Scott A. Vanstone, Handbook of Applied Cryptography, http: //www. cacr. math. uwaterloo. ca/hac/, CRC Press, 1996. NIST, FIPS Publication 46 -3: Data Encryption Standard (DES), 1999, http: //csrc. nist. gov/publications/fips 46 -3/fips 46 -3. pdf Bruce Schneier, Applied Cryptography, 2 nd edition, Wiley, 1996. US Government Dept of the Army, FM 34 -40 -2 FIELD MANUAL, 1990, http: //www. umich. edu/~umich/fm-34 -40 -2/ John Viega and Gary Mc. Graw, Building Secure Software, Addison. Wesley, 2002. CSC 382: Computer Security 76