CSC 2100 B Tutorial 9 Graph 1 Graph

CSC 2100 B Tutorial 9 Graph 1
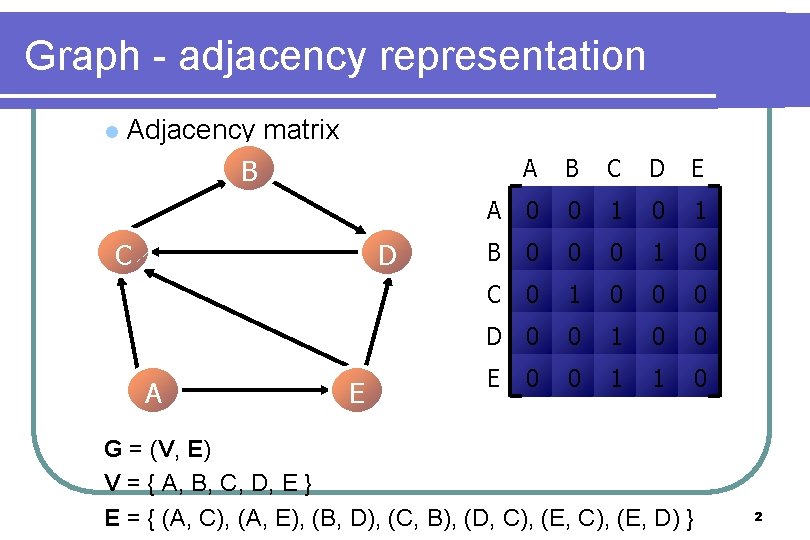
Graph - adjacency representation l Adjacency matrix A B C D E A 0 0 1 B 0 0 0 1 0 C 0 1 0 0 0 D 0 0 1 1 0 B C D A E E G = (V, E) V = { A, B, C, D, E } E = { (A, C), (A, E), (B, D), (C, B), (D, C), (E, D) } 2
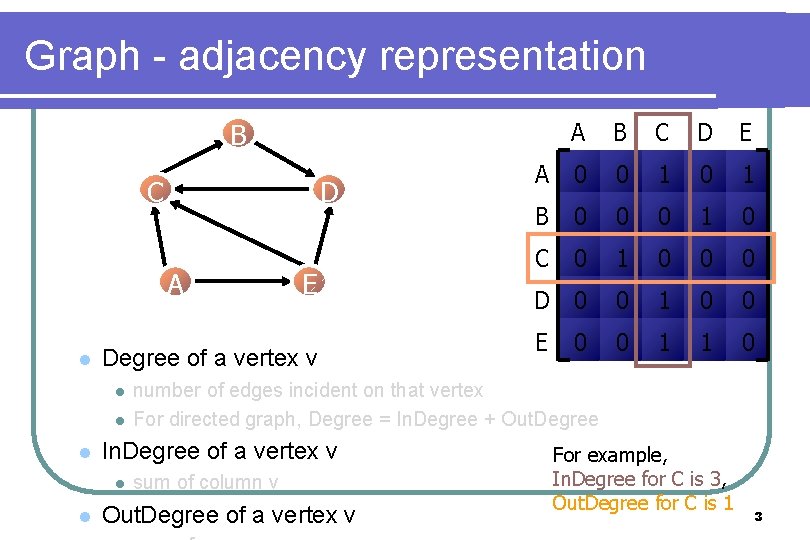
Graph - adjacency representation A B C D E A 0 0 1 B 0 0 0 1 0 C 0 1 0 0 0 D 0 0 1 1 0 B C D A l Degree of a vertex v l l l E number of edges incident on that vertex For directed graph, Degree = In. Degree + Out. Degree In. Degree of a vertex v l l E sum of column v Out. Degree of a vertex v For example, In. Degree for C is 3, Out. Degree for C is 1 3
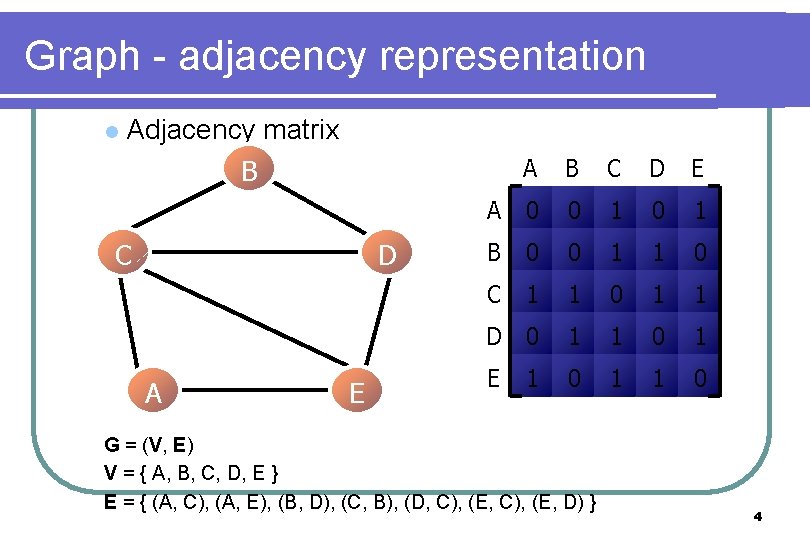
Graph - adjacency representation l Adjacency matrix A B C D E A 0 0 1 B 0 0 1 1 0 C 1 1 0 1 1 D 0 1 1 0 B C D A E E G = (V, E) V = { A, B, C, D, E } E = { (A, C), (A, E), (B, D), (C, B), (D, C), (E, D) } 4
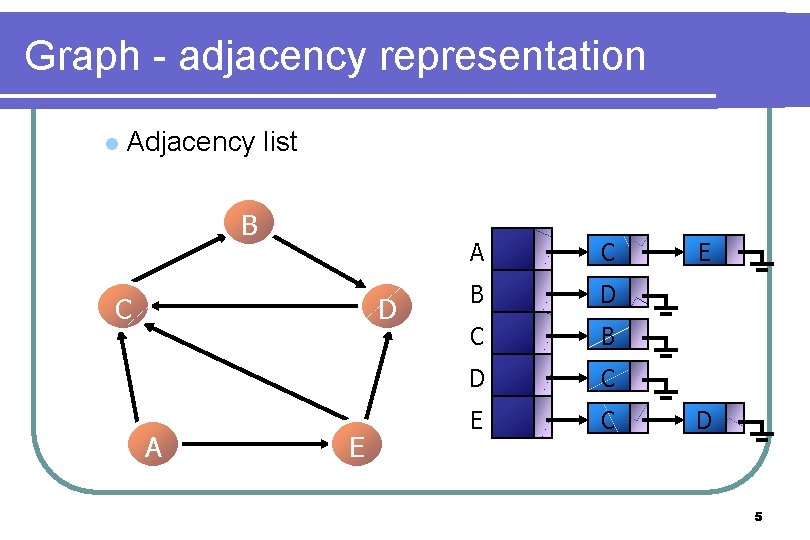
Graph - adjacency representation l Adjacency list B C D A E A C B D C E D 5
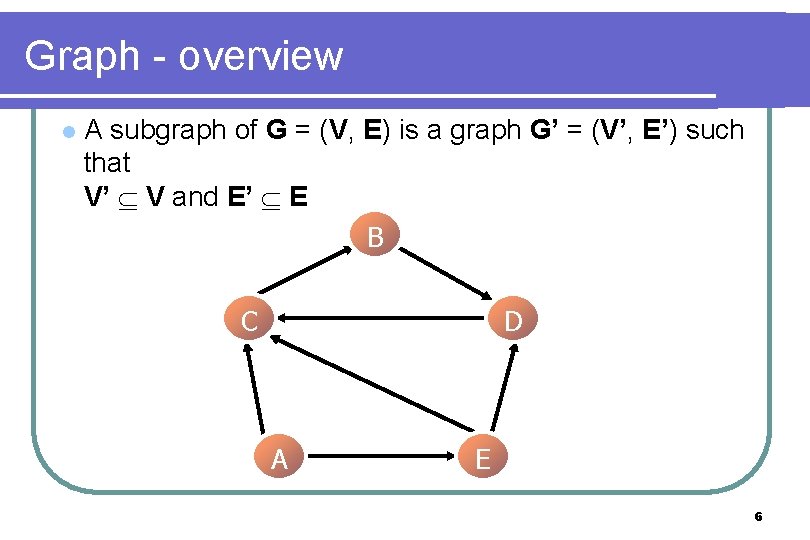
Graph - overview l A subgraph of G = (V, E) is a graph G’ = (V’, E’) such that V’ V and E’ E B C D A E 6
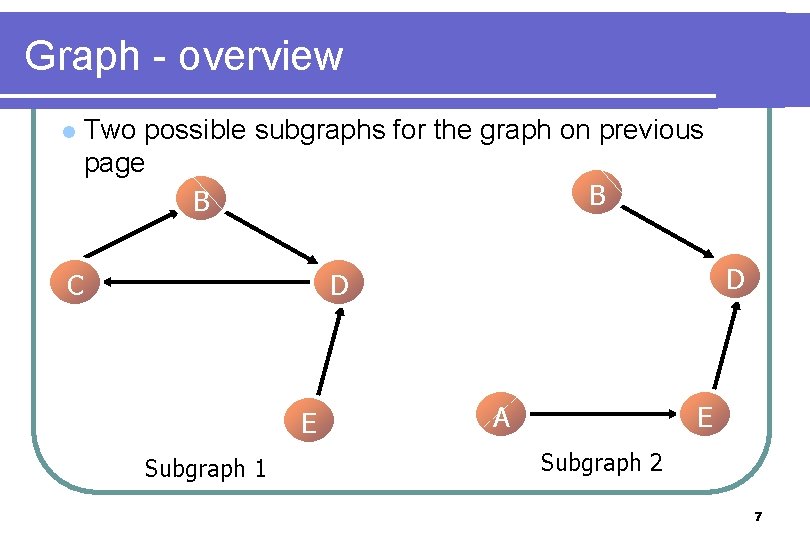
Graph - overview l Two possible subgraphs for the graph on previous page B B C D D E Subgraph 1 A E Subgraph 2 7
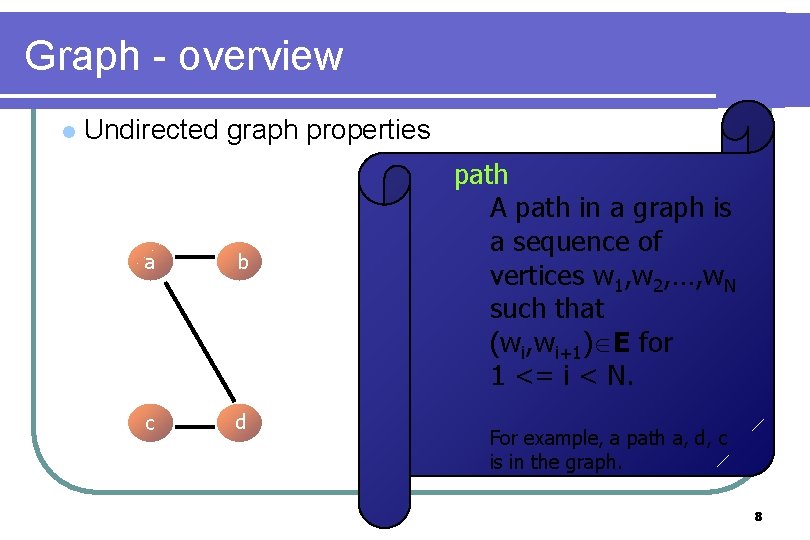
Graph - overview l Undirected graph properties a b c d path A path in a graph is a sequence of vertices w 1, w 2, …, w. N such that (wi, wi+1) E for 1 <= i < N. For example, a path a, d, c is in the graph. 8
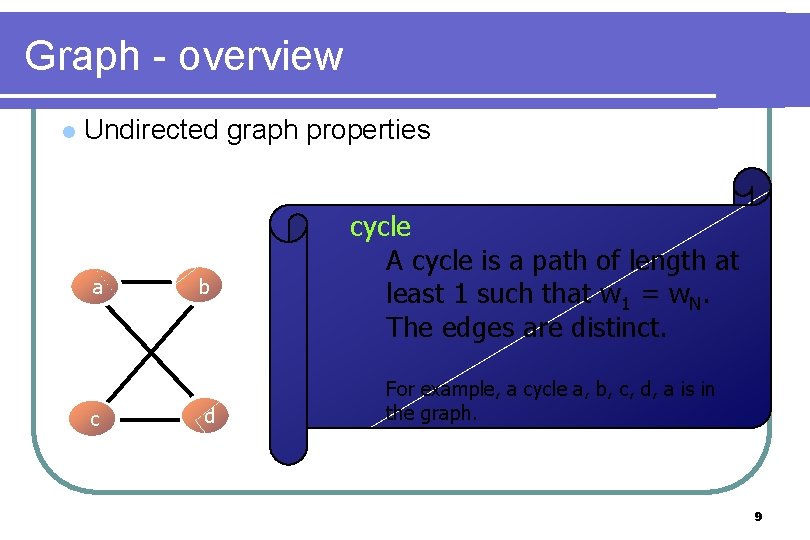
Graph - overview l Undirected graph properties a c b d cycle A cycle is a path of length at least 1 such that w 1 = w. N. The edges are distinct. For example, a cycle a, b, c, d, a is in the graph. 9
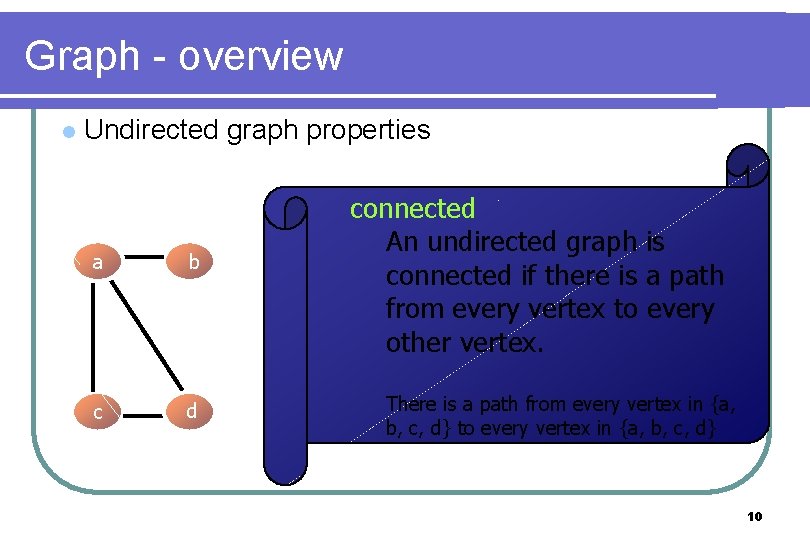
Graph - overview l Undirected graph properties a b c d connected An undirected graph is connected if there is a path from every vertex to every other vertex. There is a path from every vertex in {a, b, c, d} to every vertex in {a, b, c, d} 10
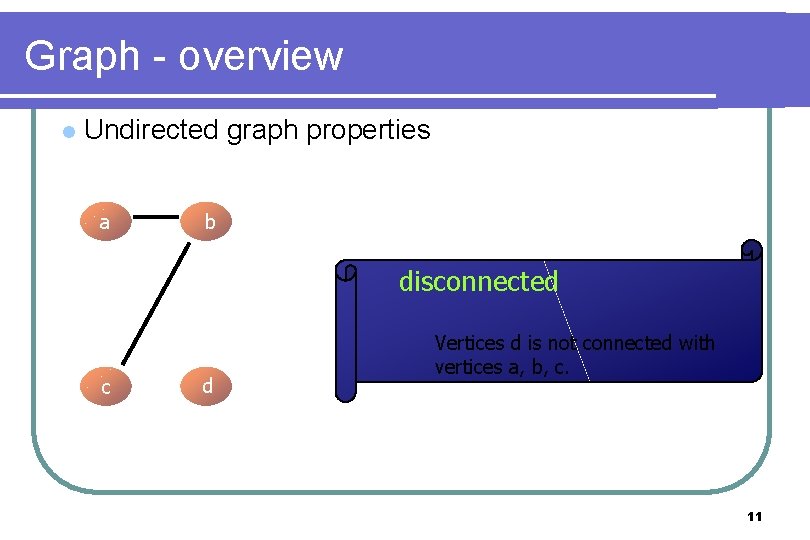
Graph - overview l Undirected graph properties a b disconnected c d Vertices d is not connected with vertices a, b, c. 11
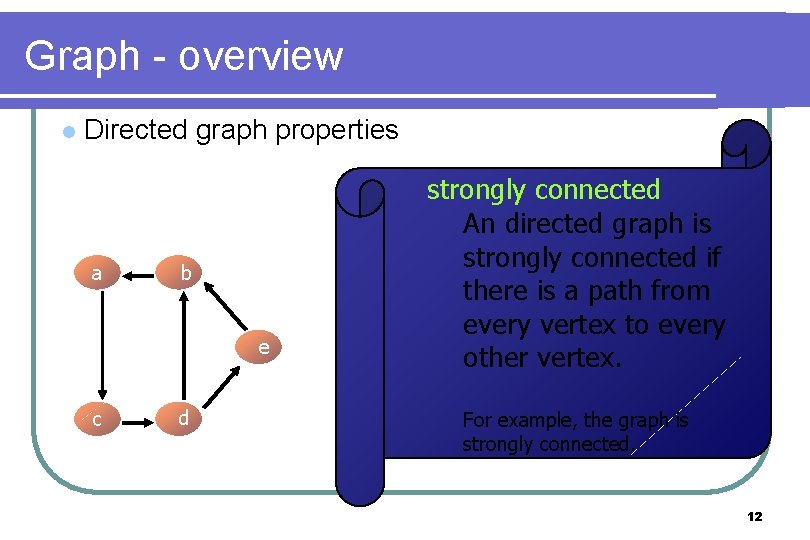
Graph - overview l Directed graph properties a b e c d strongly connected An directed graph is strongly connected if there is a path from every vertex to every other vertex. For example, the graph is strongly connected. 12
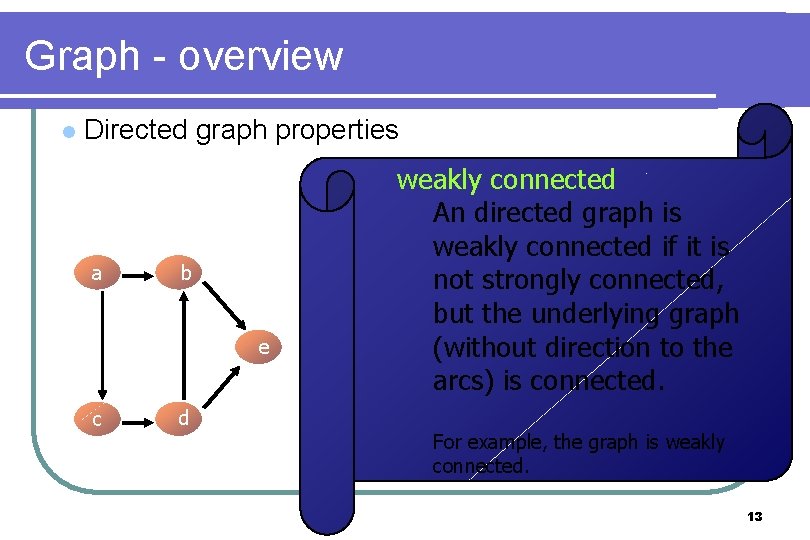
Graph - overview l Directed graph properties a b e c d weakly connected An directed graph is weakly connected if it is not strongly connected, but the underlying graph (without direction to the arcs) is connected. For example, the graph is weakly connected. 13
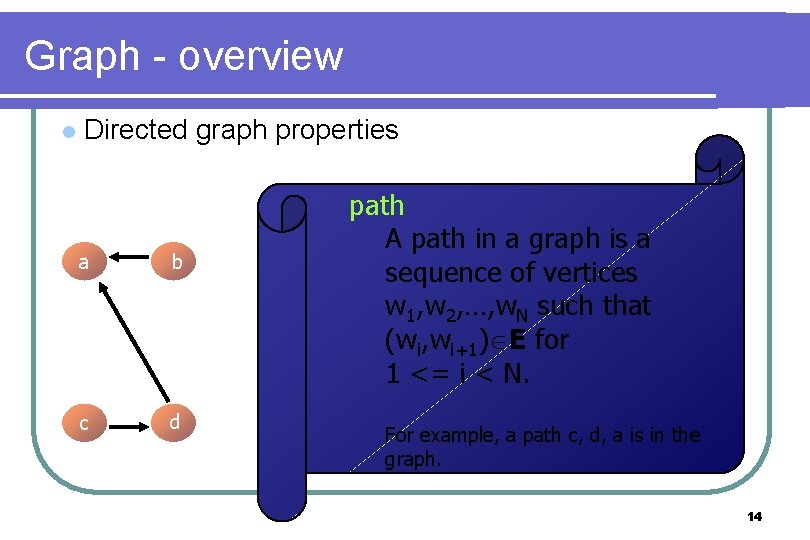
Graph - overview l Directed graph properties a b c d path A path in a graph is a sequence of vertices w 1, w 2, …, w. N such that (wi, wi+1) E for 1 <= i < N. For example, a path c, d, a is in the graph. 14
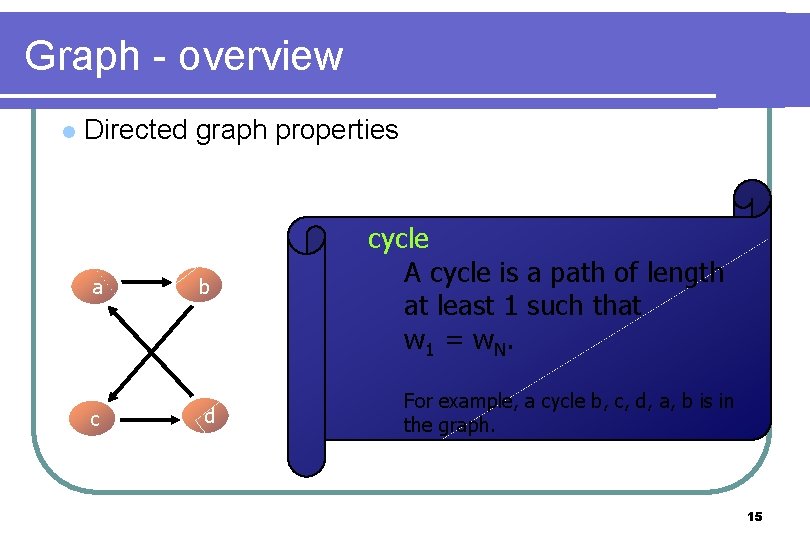
Graph - overview l Directed graph properties a c b d cycle A cycle is a path of length at least 1 such that w 1 = w. N. For example, a cycle b, c, d, a, b is in the graph. 15
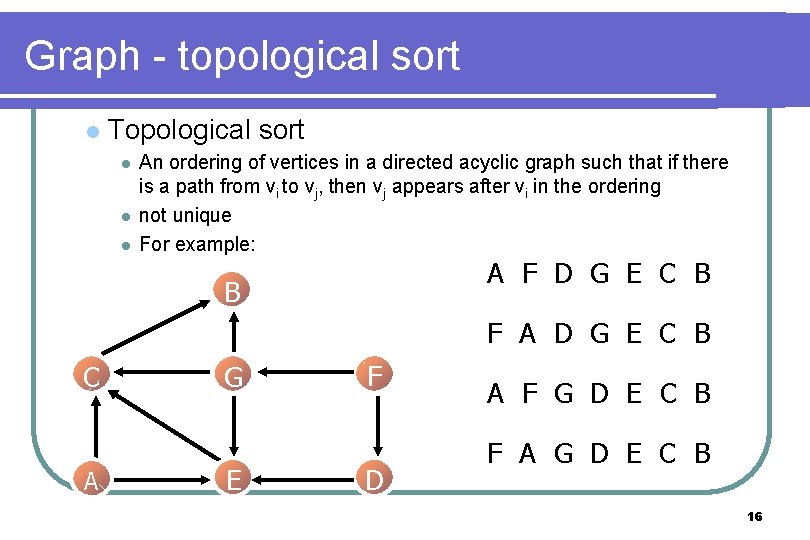
Graph - topological sort l Topological sort l l l An ordering of vertices in a directed acyclic graph such that if there is a path from vi to vj, then vj appears after vi in the ordering not unique For example: A F D G E C B B F A D G E C B C A G E F D A F G D E C B F A G D E C B 16

Graph - topological sort l Algorithm A queue is used l Steps: l Initialize counter to 0 l Calculate the indegree for each vertex l Enqueue all vertices with indegree = 0 l While the queue is not empty l l l Dequeue a vertex X from the queue Increment counter by 1 Vertex X is the counter’th element in the sort For each vertex Y that is adjacent to vertex X, decrement its indegree by one, if its indegree is zero, enqueue the vertex Y. 17
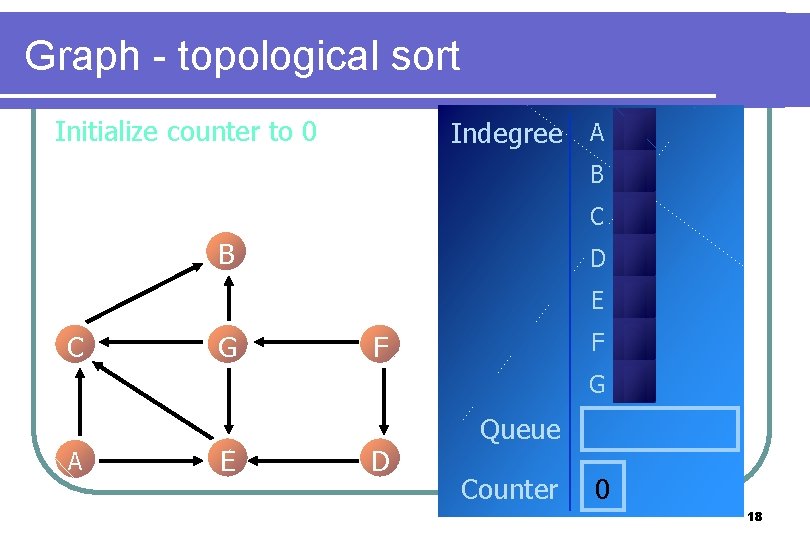
Graph - topological sort Initialize counter to 0 Indegree A B C B D E C G F F G A E D Queue Counter 0 18
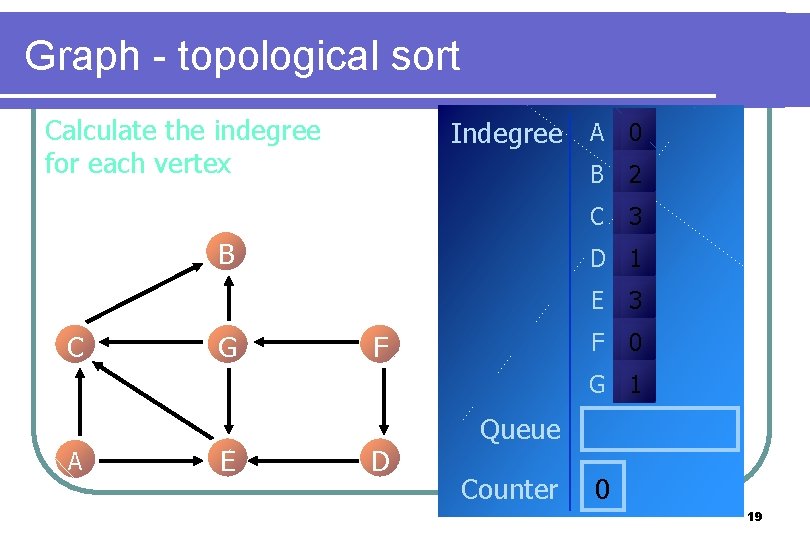
Graph - topological sort Calculate the indegree for each vertex Indegree A 0 B C G B 2 C 3 D 1 F E 3 F 0 G 1 A E D Queue Counter 0 19
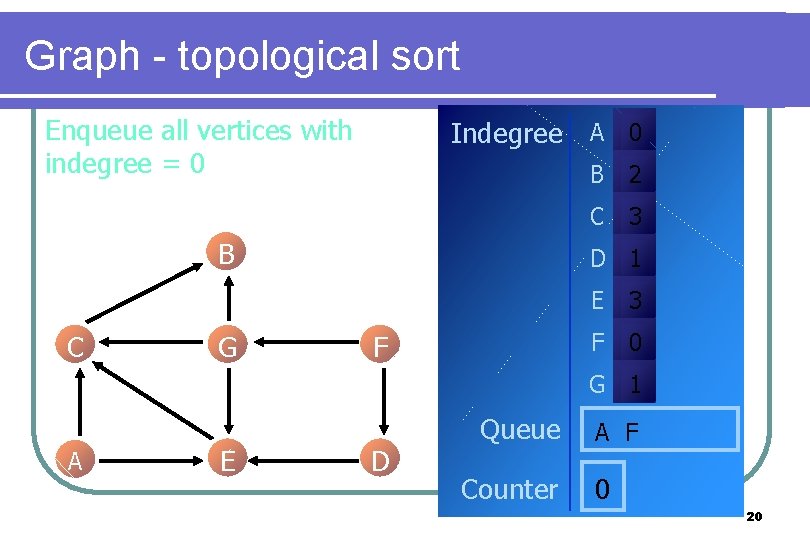
Graph - topological sort Enqueue all vertices with indegree = 0 Indegree A 0 B C G B 2 C 3 D 1 F E 3 F 0 G 1 A E D Queue Counter A F 0 20
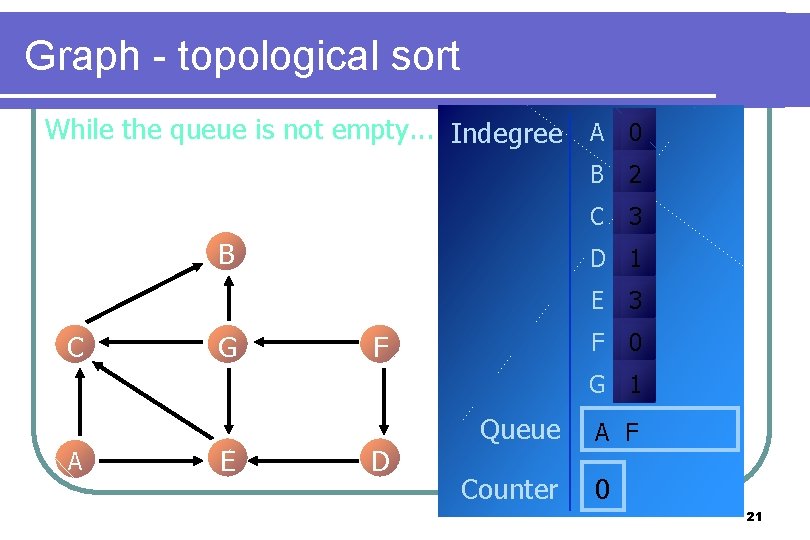
Graph - topological sort While the queue is not empty. . . Indegree A 0 B C G B 2 C 3 D 1 F E 3 F 0 G 1 A E D Queue Counter A F 0 21
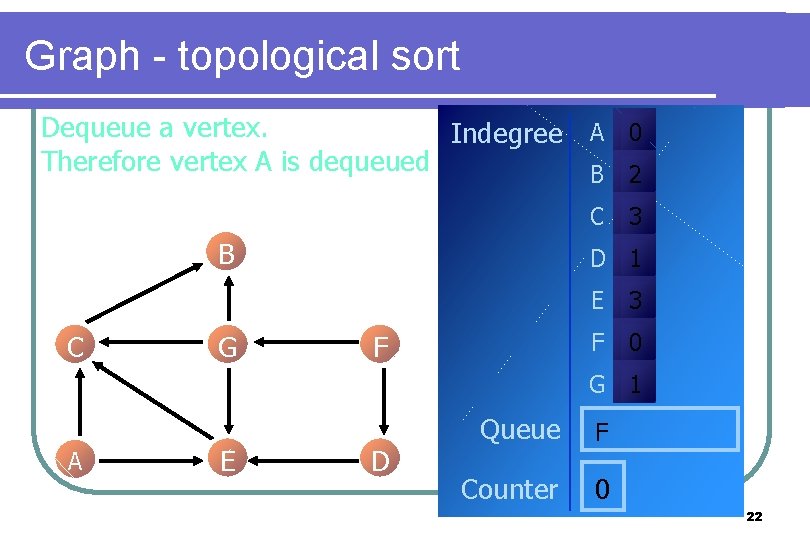
Graph - topological sort Dequeue a vertex. Indegree A 0 Therefore vertex A is dequeued B 2 C B C G 3 D 1 F E 3 F 0 G 1 A E D Queue F Counter 0 22
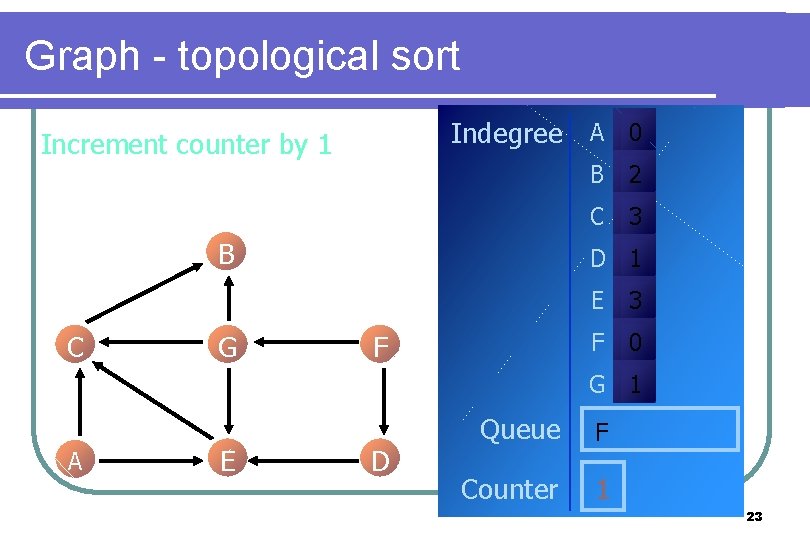
Graph - topological sort Indegree A 0 Increment counter by 1 B C G B 2 C 3 D 1 F E 3 F 0 G 1 A E D Queue F Counter 1 23
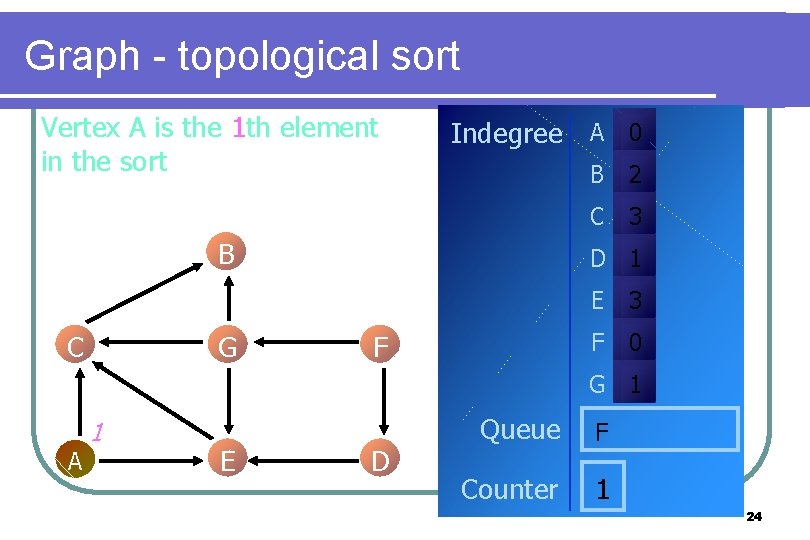
Graph - topological sort Vertex A is the 1 th element in the sort Indegree A 0 B C G B 2 C 3 D 1 F E 3 F 0 G 1 A 1 E D Queue F Counter 1 24
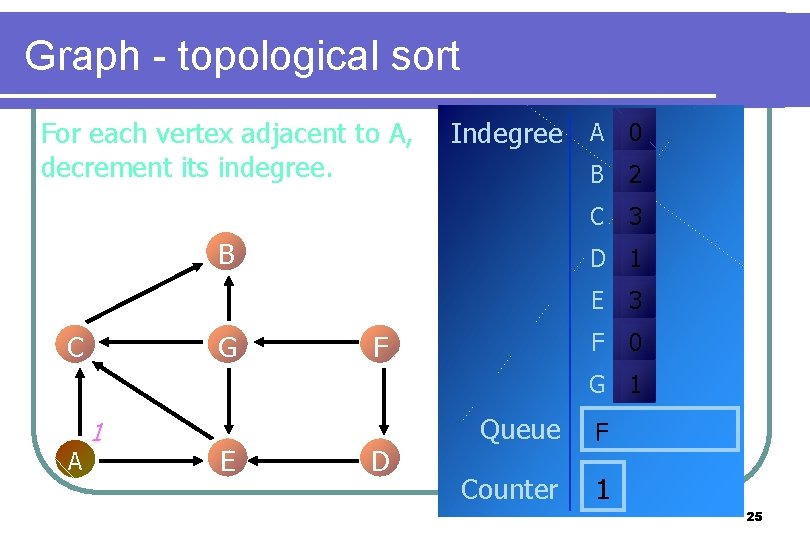
Graph - topological sort For each vertex adjacent to A, decrement its indegree. Indegree A 0 B C G B 2 C 3 D 1 F E 3 F 0 G 1 A 1 E D Queue F Counter 1 25
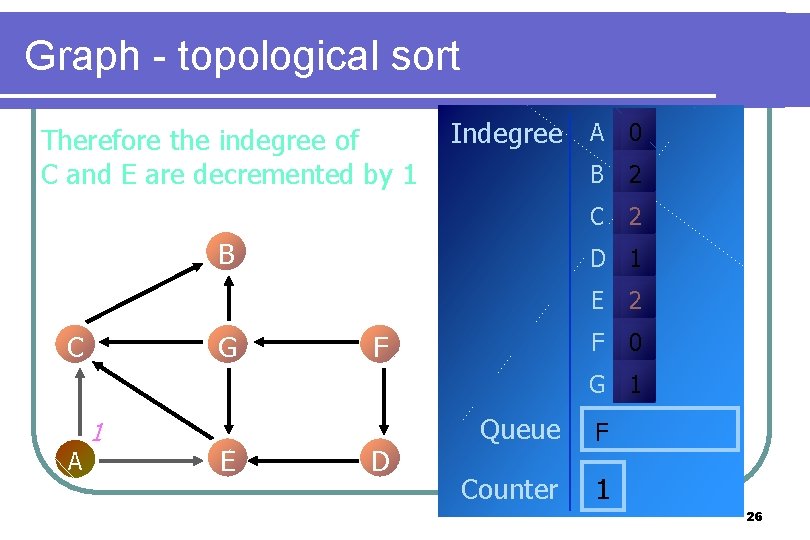
Graph - topological sort Therefore the indegree of C and E are decremented by 1 Indegree A 0 B C G B 2 C 2 D 1 F E 2 F 0 G 1 A 1 E D Queue F Counter 1 26
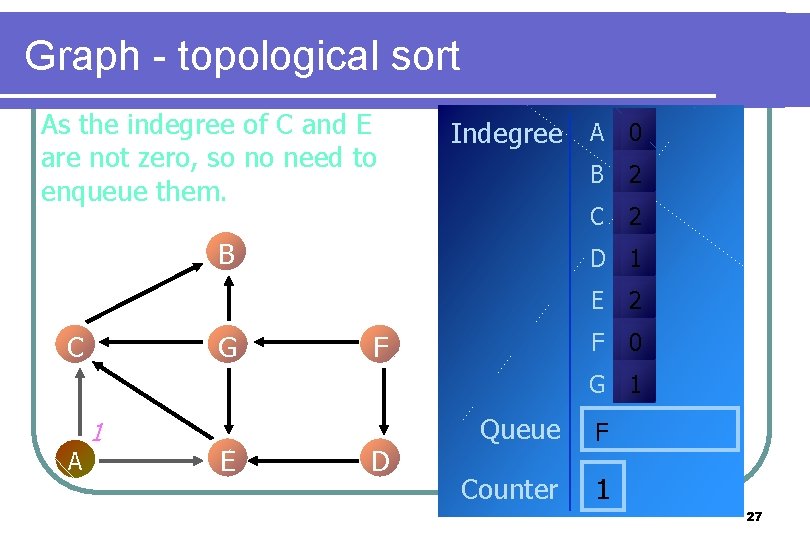
Graph - topological sort As the indegree of C and E are not zero, so no need to enqueue them. Indegree A 0 B C G B 2 C 2 D 1 F E 2 F 0 G 1 A 1 E D Queue F Counter 1 27
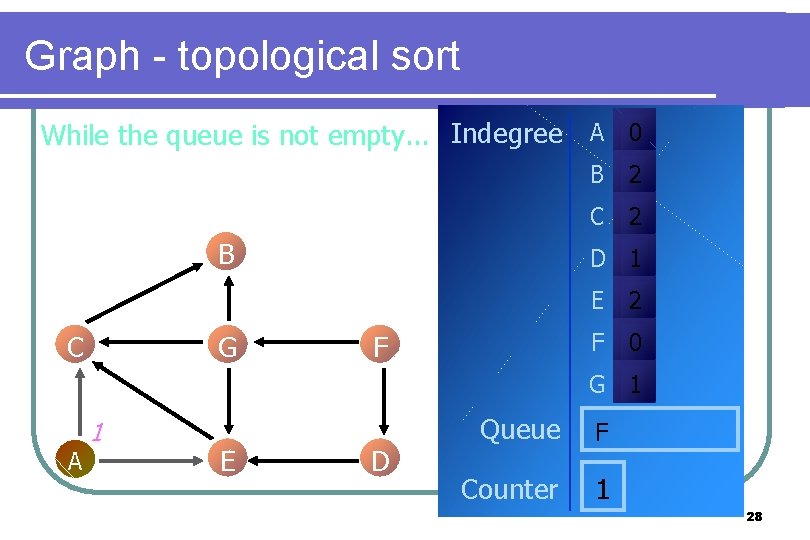
Graph - topological sort While the queue is not empty. . . Indegree A 0 B C G B 2 C 2 D 1 F E 2 F 0 G 1 A 1 E D Queue F Counter 1 28
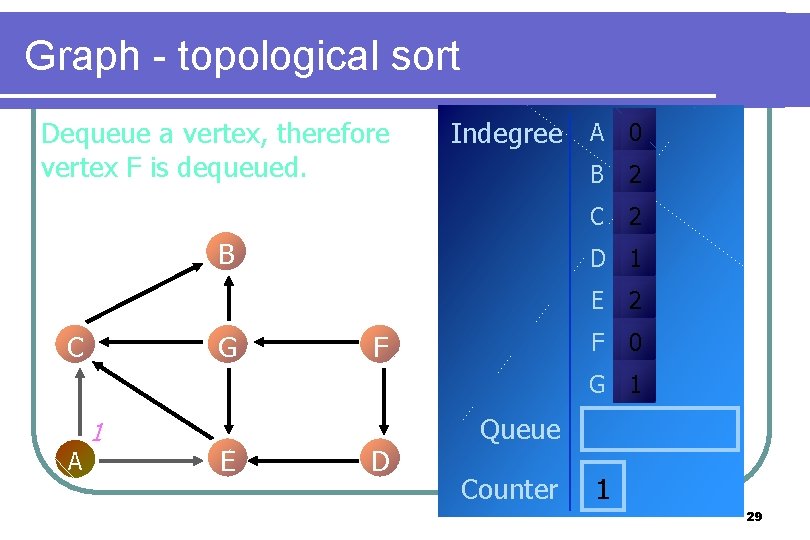
Graph - topological sort Dequeue a vertex, therefore vertex F is dequeued. Indegree A 0 B C G B 2 C 2 D 1 F E 2 F 0 G 1 A 1 E D Queue Counter 1 29
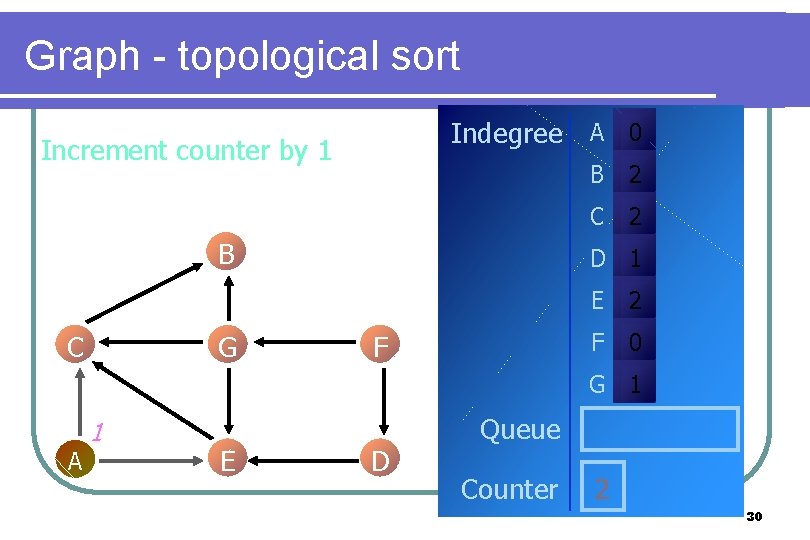
Graph - topological sort Indegree A 0 Increment counter by 1 B C G B 2 C 2 D 1 F E 2 F 0 G 1 A 1 E D Queue Counter 2 30
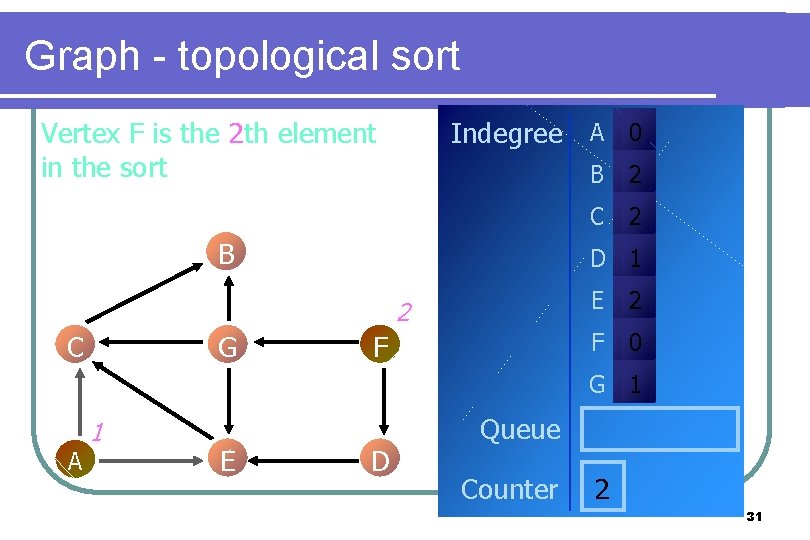
Graph - topological sort Vertex F is the 2 th element in the sort Indegree A 0 B G 2 C 2 D 1 2 C B F E 2 F 0 G 1 A 1 E D Queue Counter 2 31
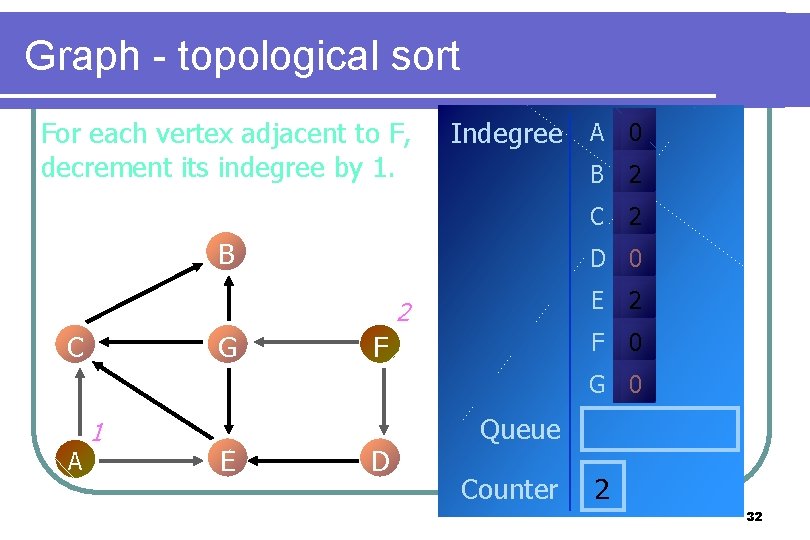
Graph - topological sort For each vertex adjacent to F, decrement its indegree by 1. Indegree A 0 B G 2 C 2 D 0 2 C B F E 2 F 0 G 0 A 1 E D Queue Counter 2 32
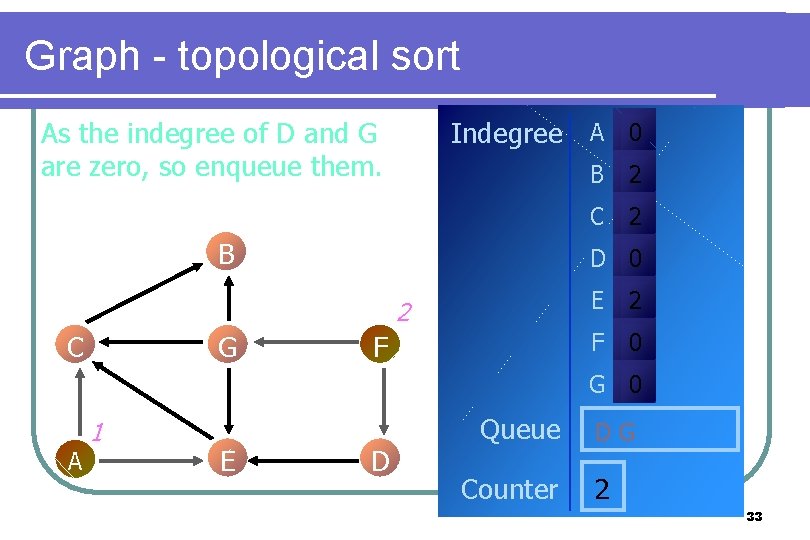
Graph - topological sort As the indegree of D and G are zero, so enqueue them. Indegree A 0 B G 2 C 2 D 0 2 C B F E 2 F 0 G 0 A 1 E D Queue Counter DG 2 33
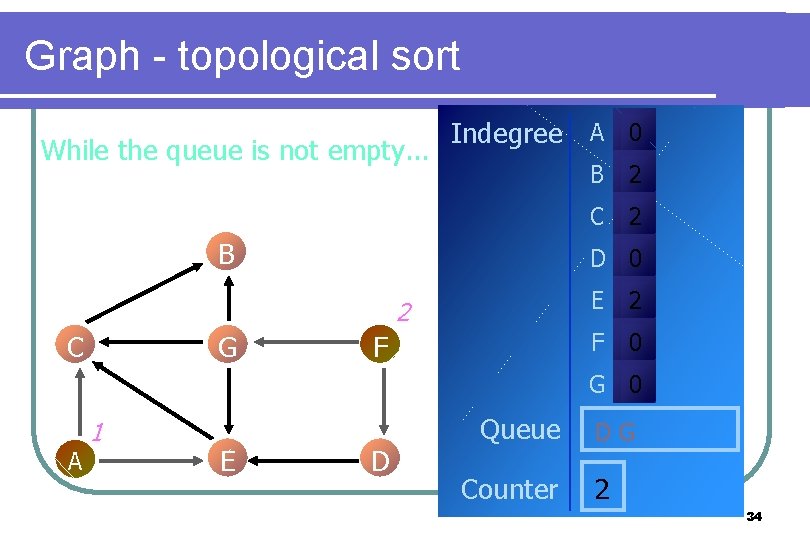
Graph - topological sort While the queue is not empty. . . Indegree A 0 B G 2 C 2 D 0 2 C B F E 2 F 0 G 0 A 1 E D Queue Counter DG 2 34
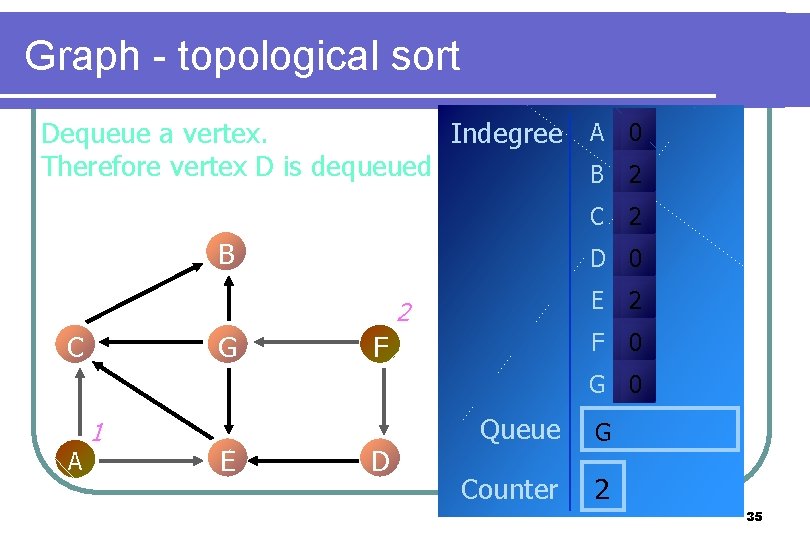
Graph - topological sort Dequeue a vertex. Indegree A 0 Therefore vertex D is dequeued B 2 C B D 0 2 C G 2 F E 2 F 0 G 0 A 1 E D Queue G Counter 2 35
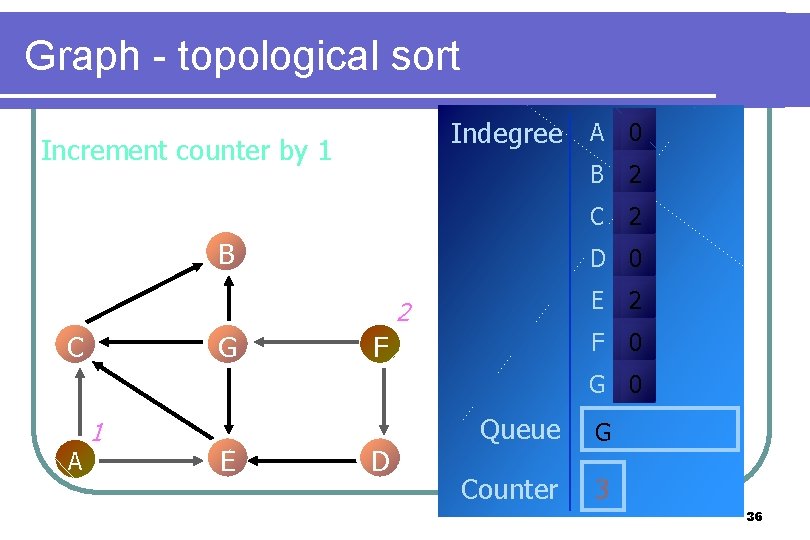
Graph - topological sort Indegree A 0 Increment counter by 1 B G 2 C 2 D 0 2 C B F E 2 F 0 G 0 A 1 E D Queue G Counter 3 36
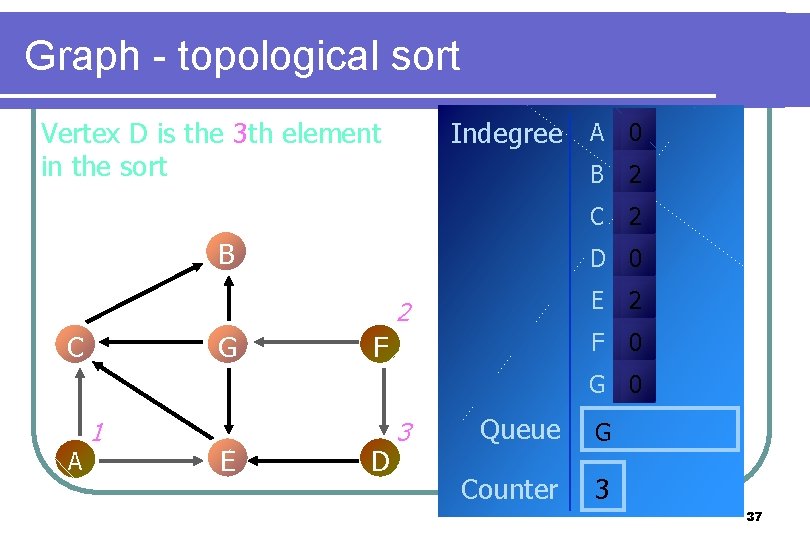
Graph - topological sort Vertex D is the 3 th element in the sort Indegree A 0 B G 2 C 2 D 0 2 C B F E 2 F 0 G 0 A 1 E D 3 Queue G Counter 3 37
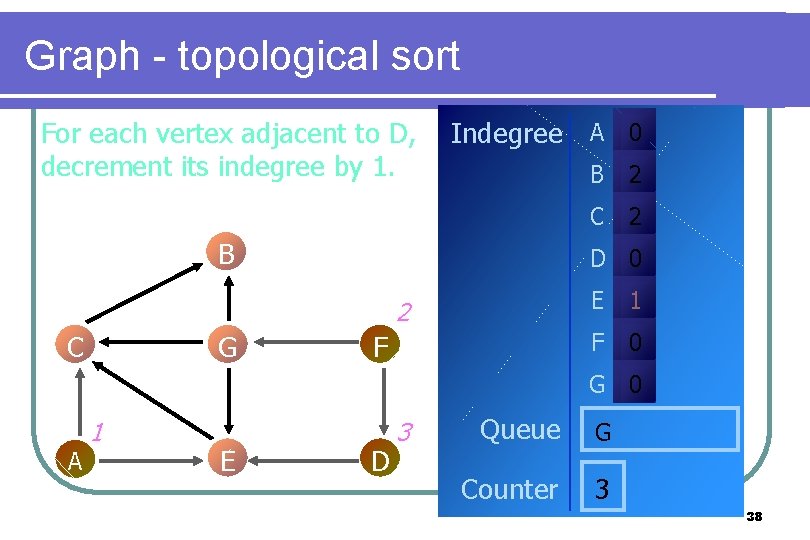
Graph - topological sort For each vertex adjacent to D, decrement its indegree by 1. Indegree A 0 B G 2 C 2 D 0 2 C B F E 1 F 0 G 0 A 1 E D 3 Queue G Counter 3 38
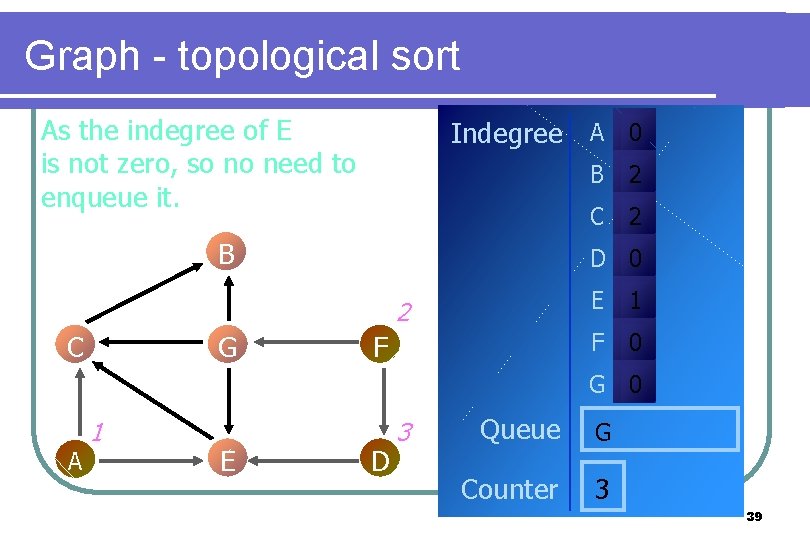
Graph - topological sort As the indegree of E is not zero, so no need to enqueue it. Indegree A 0 B G 2 C 2 D 0 2 C B F E 1 F 0 G 0 A 1 E D 3 Queue G Counter 3 39
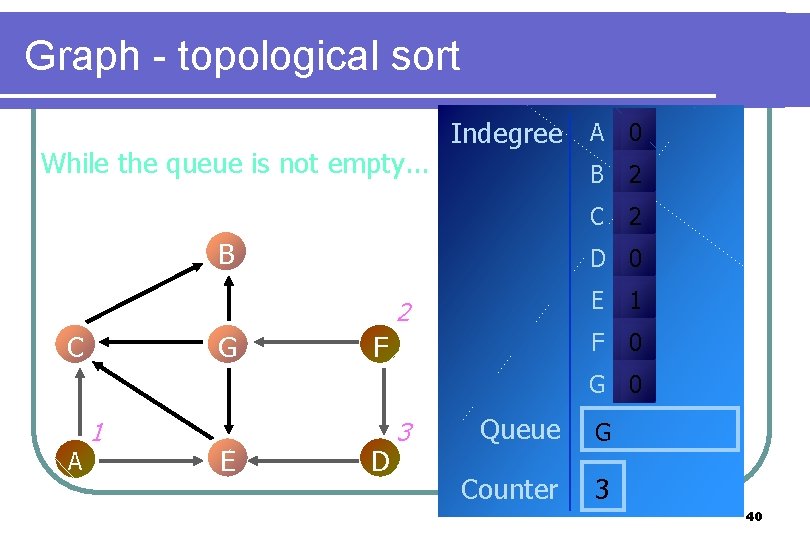
Graph - topological sort While the queue is not empty. . . Indegree A 0 B G 2 C 2 D 0 2 C B F E 1 F 0 G 0 A 1 E D 3 Queue G Counter 3 40
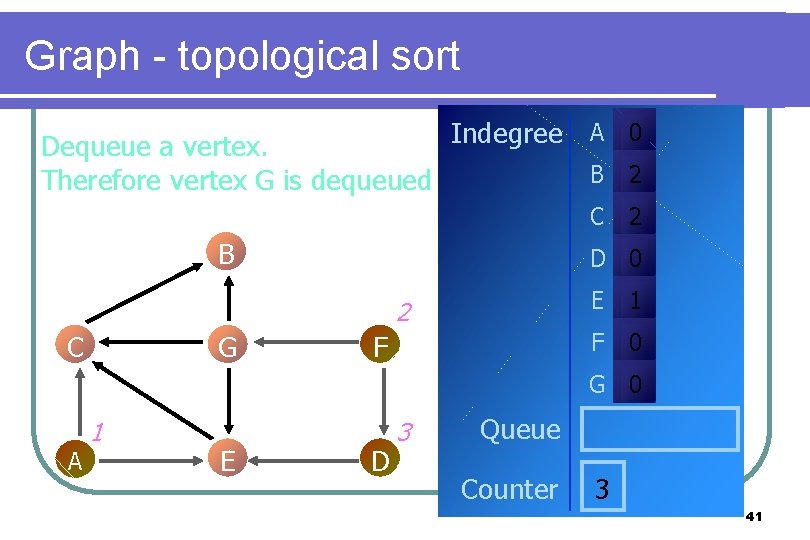
Graph - topological sort Dequeue a vertex. Therefore vertex G is dequeued Indegree A 0 B G 2 C 2 D 0 2 C B F E 1 F 0 G 0 A 1 E D 3 Queue Counter 3 41
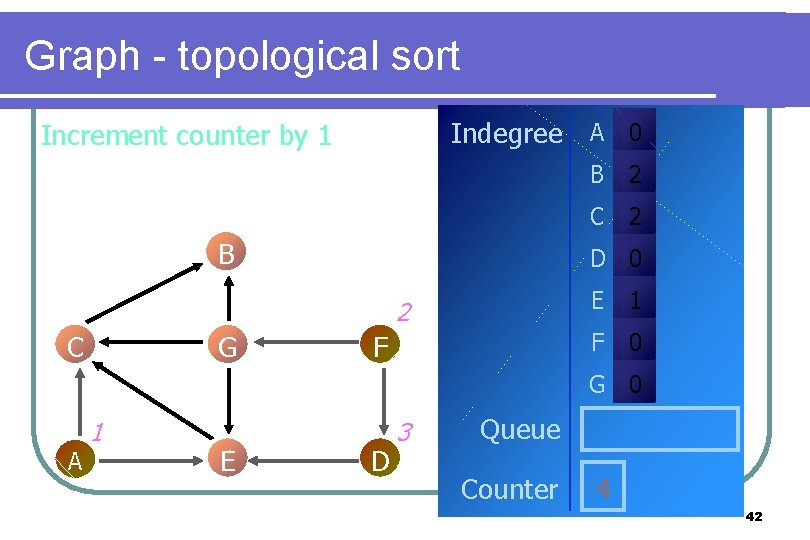
Graph - topological sort Indegree A 0 Increment counter by 1 B G 2 C 2 D 0 2 C B F E 1 F 0 G 0 A 1 E D 3 Queue Counter 4 42
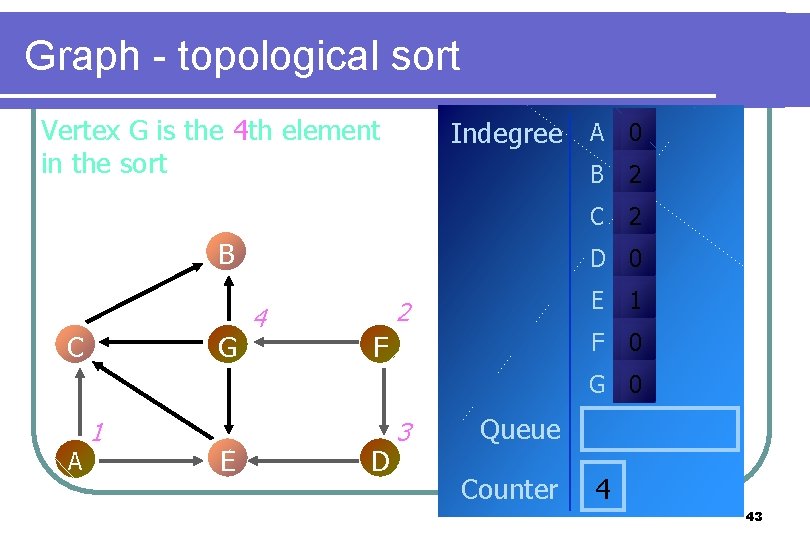
Graph - topological sort Vertex G is the 4 th element in the sort Indegree A 0 B C G B 2 C 2 D 0 4 2 F E 1 F 0 G 0 A 1 E D 3 Queue Counter 4 43
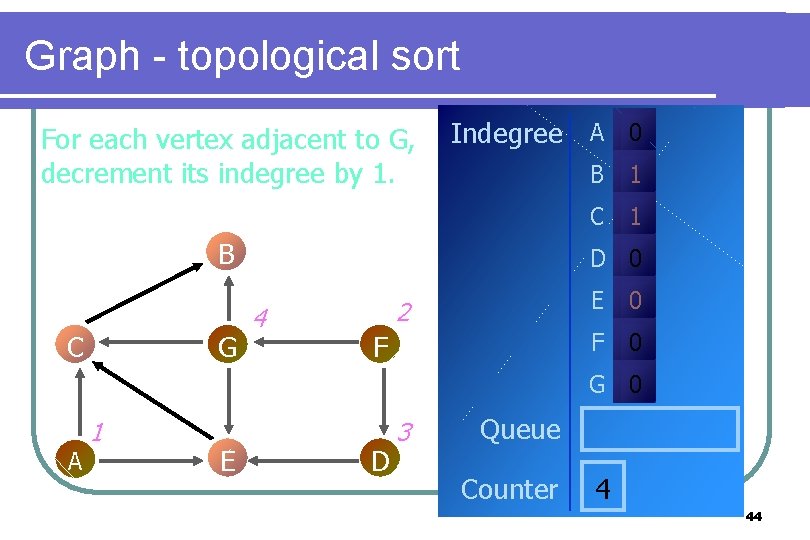
Graph - topological sort For each vertex adjacent to G, decrement its indegree by 1. Indegree A 0 B C G B 1 C 1 D 0 4 2 F E 0 F 0 G 0 A 1 E D 3 Queue Counter 4 44
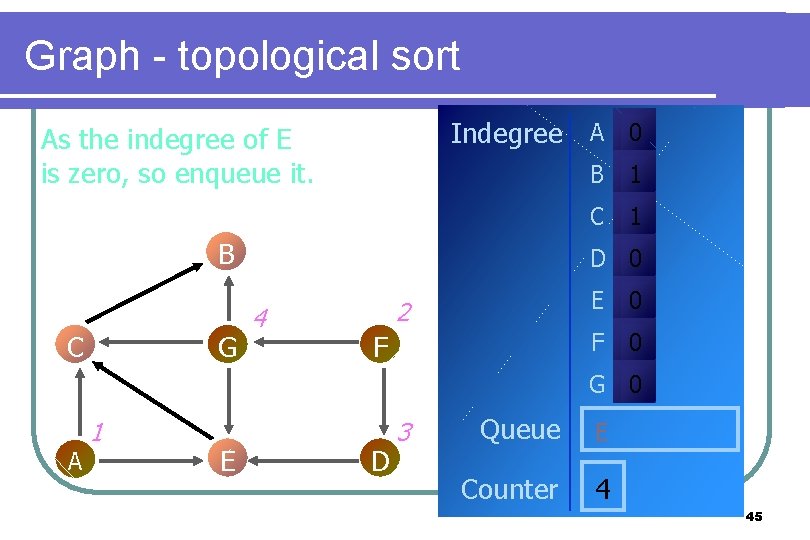
Graph - topological sort Indegree A 0 As the indegree of E is zero, so enqueue it. B C G B 1 C 1 D 0 4 2 F E 0 F 0 G 0 A 1 E D 3 Queue E Counter 4 45
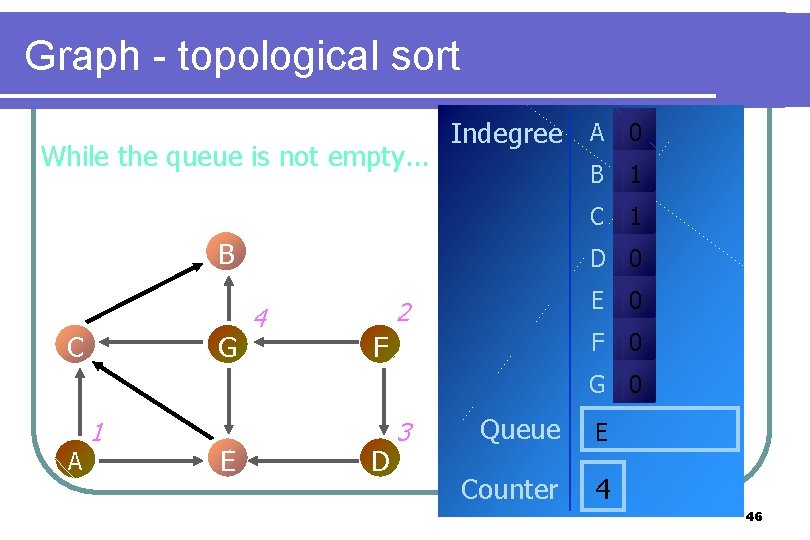
Graph - topological sort While the queue is not empty. . . Indegree A 0 B C G B 1 C 1 D 0 4 2 F E 0 F 0 G 0 A 1 E D 3 Queue E Counter 4 46
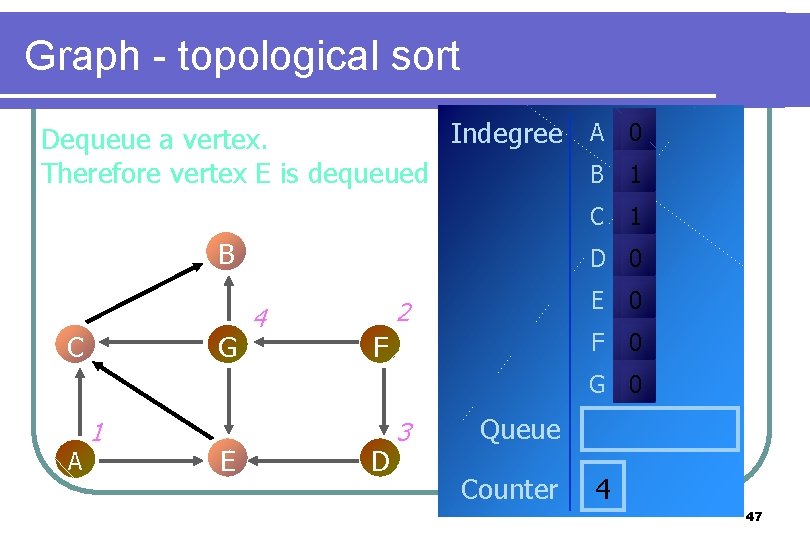
Graph - topological sort Indegree A 0 Dequeue a vertex. Therefore vertex E is dequeued B 1 C B C G 1 D 0 4 2 F E 0 F 0 G 0 A 1 E D 3 Queue Counter 4 47
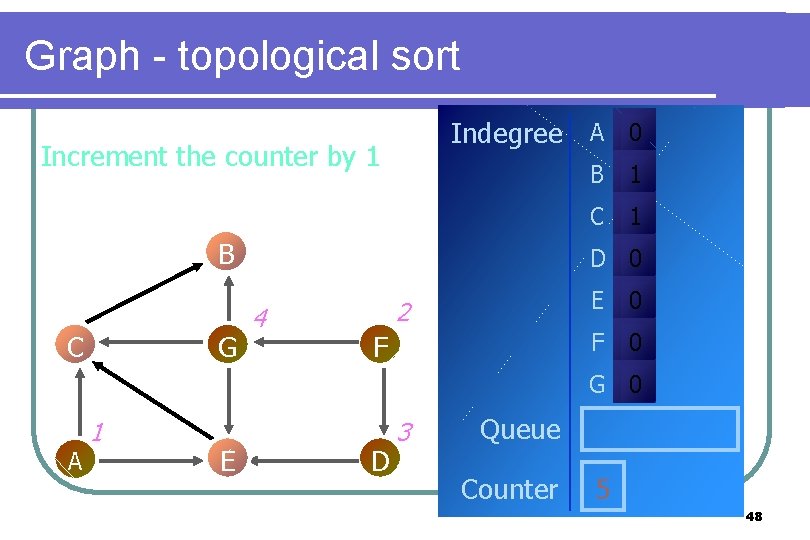
Graph - topological sort Indegree A 0 Increment the counter by 1 B C G B 1 C 1 D 0 4 2 F E 0 F 0 G 0 A 1 E D 3 Queue Counter 5 48
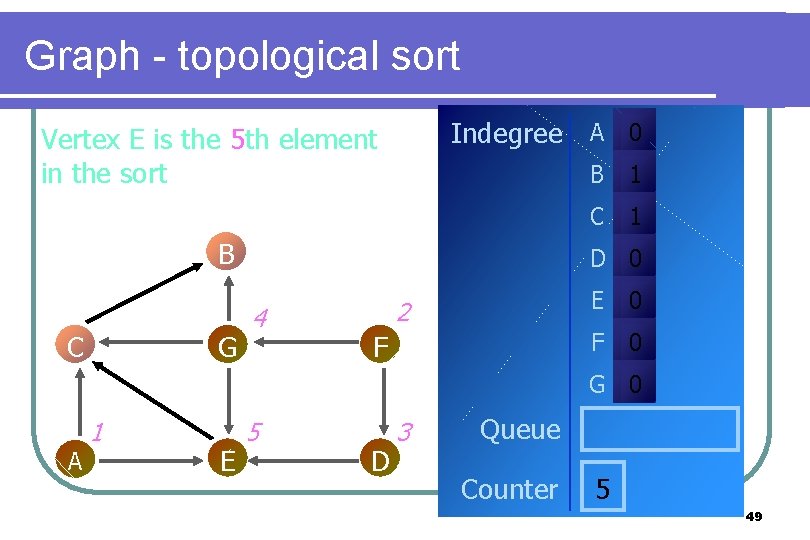
Graph - topological sort Indegree A 0 Vertex E is the 5 th element in the sort B C G B 1 C 1 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 5 49
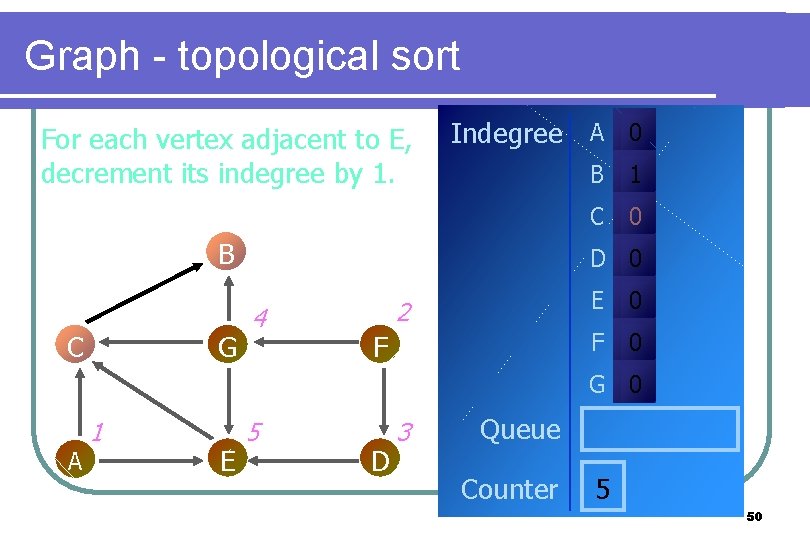
Graph - topological sort For each vertex adjacent to E, decrement its indegree by 1. Indegree A 0 B C G B 1 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 5 50
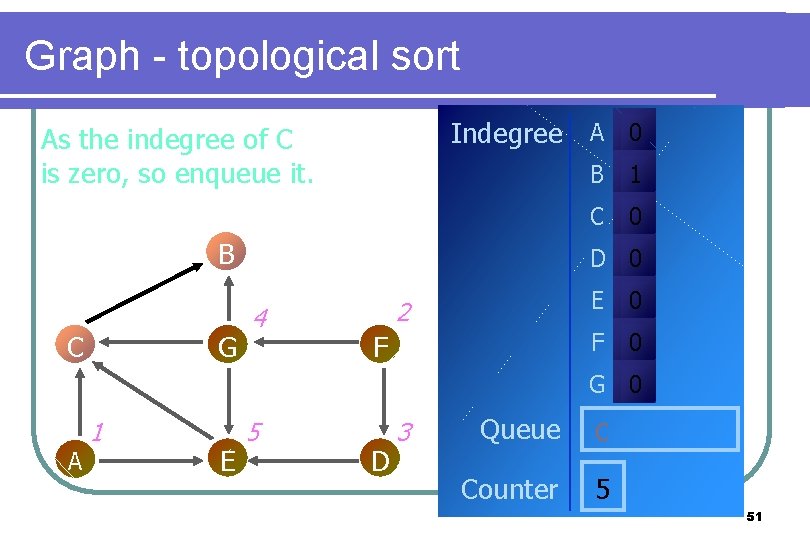
Graph - topological sort Indegree A 0 As the indegree of C is zero, so enqueue it. B C G B 1 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue C Counter 5 51
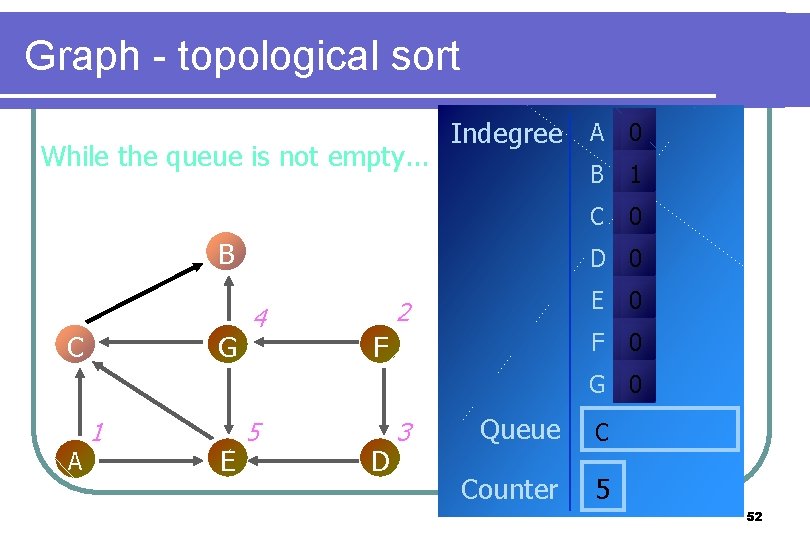
Graph - topological sort While the queue is not empty. . . Indegree A 0 B C G B 1 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue C Counter 5 52
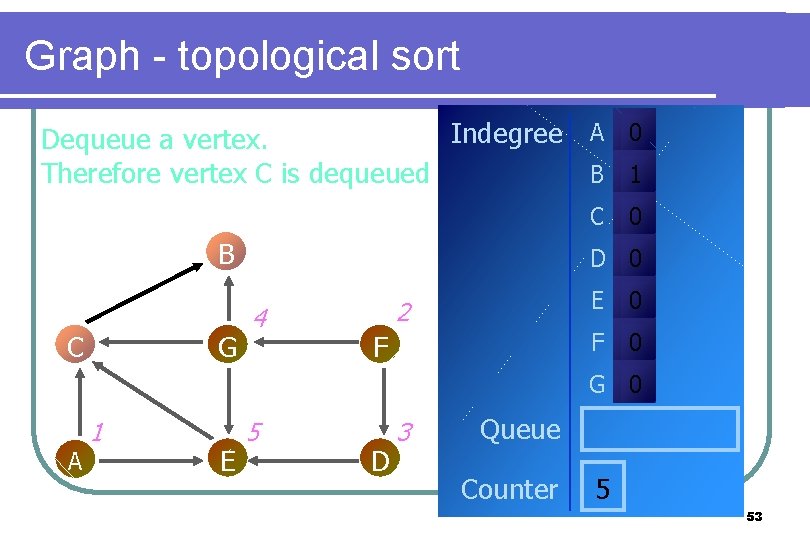
Graph - topological sort Indegree A 0 Dequeue a vertex. Therefore vertex C is dequeued B 1 C B C G 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 5 53
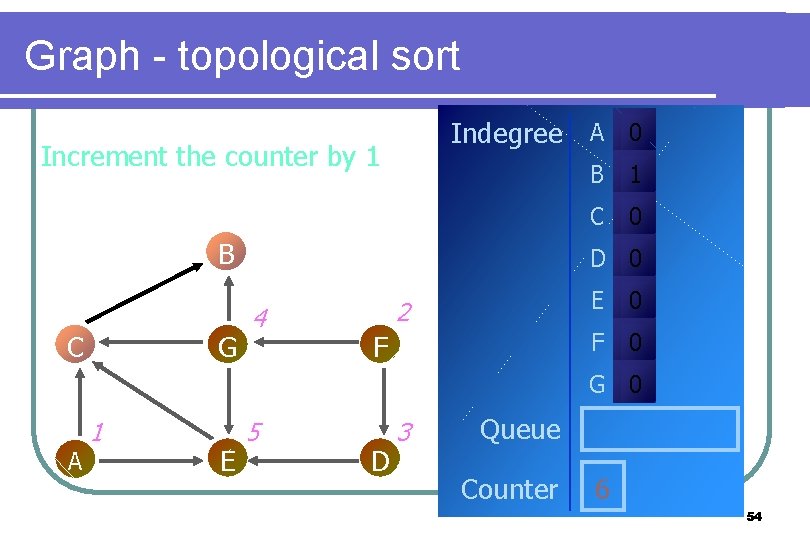
Graph - topological sort Indegree A 0 Increment the counter by 1 B C G B 1 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 6 54
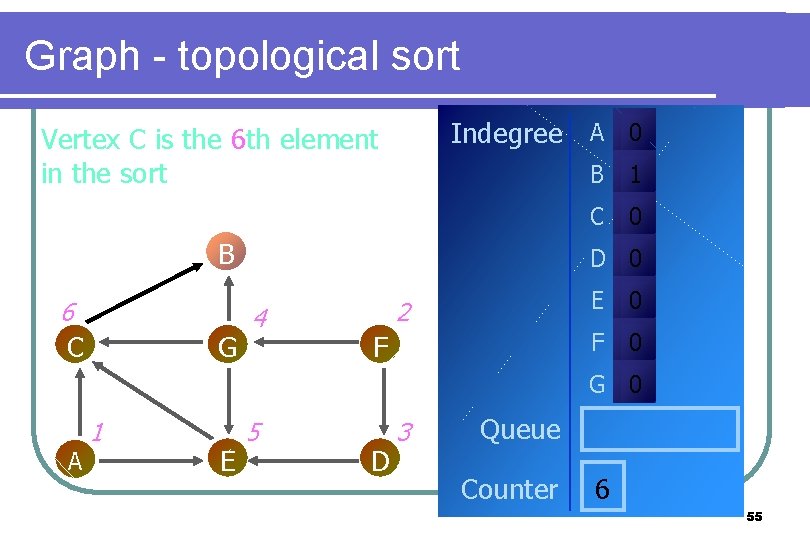
Graph - topological sort Indegree A 0 Vertex C is the 6 th element in the sort B 6 C G B 1 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 6 55
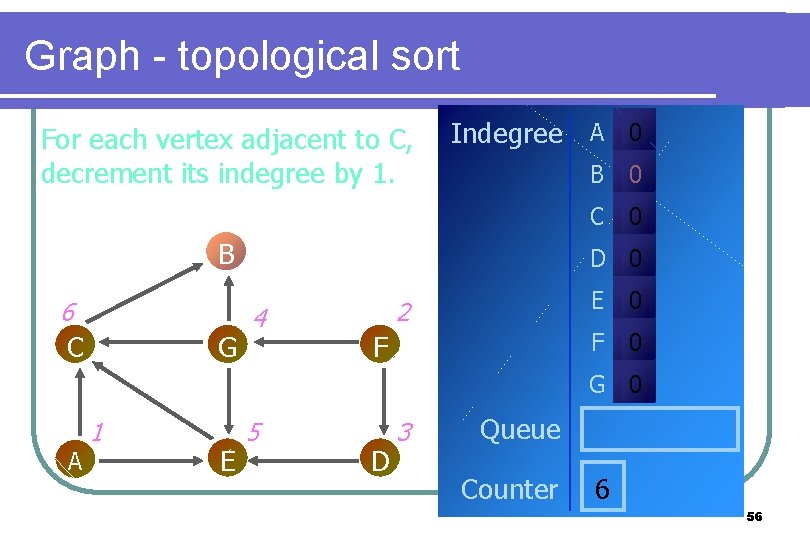
Graph - topological sort For each vertex adjacent to C, decrement its indegree by 1. Indegree A 0 B 6 C G B 0 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 6 56
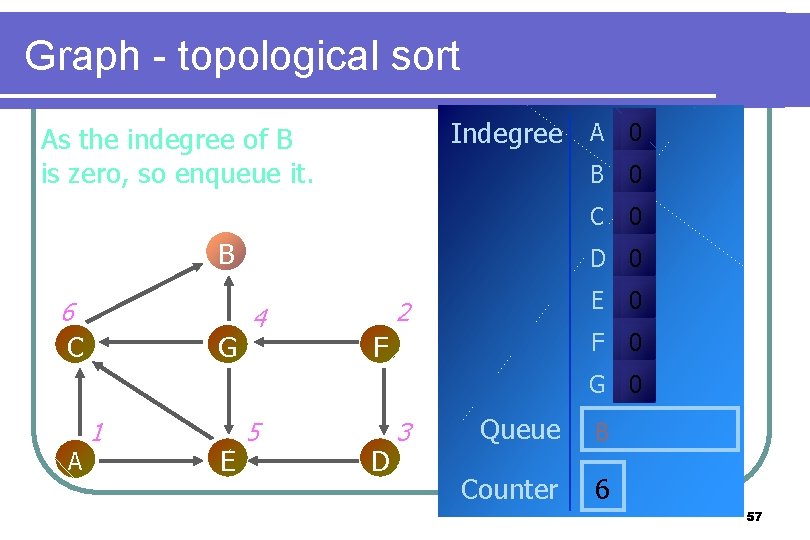
Graph - topological sort Indegree A 0 As the indegree of B is zero, so enqueue it. B 6 C G B 0 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue B Counter 6 57
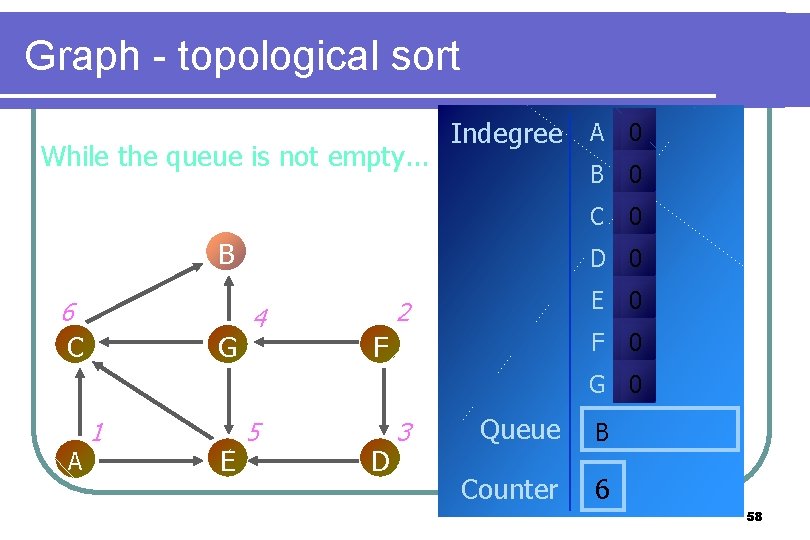
Graph - topological sort While the queue is not empty. . . Indegree A 0 B 6 C G B 0 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue B Counter 6 58
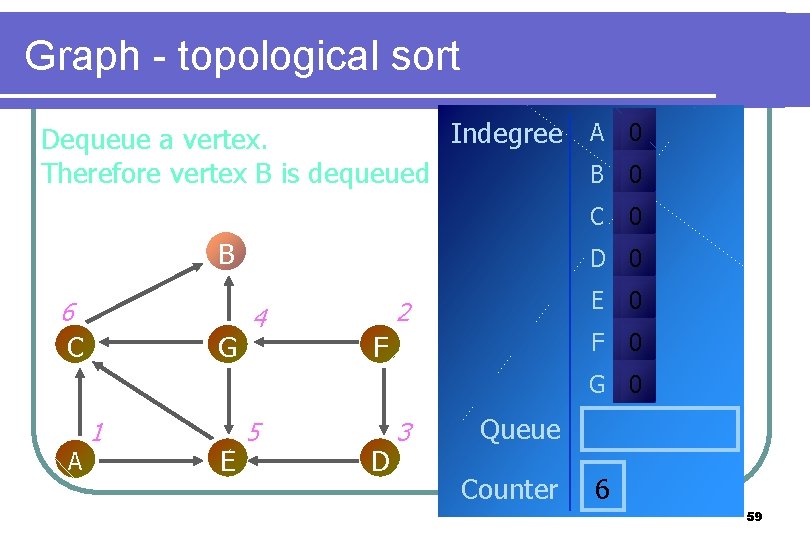
Graph - topological sort Indegree A 0 Dequeue a vertex. Therefore vertex B is dequeued B 0 C B 6 C G 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 6 59
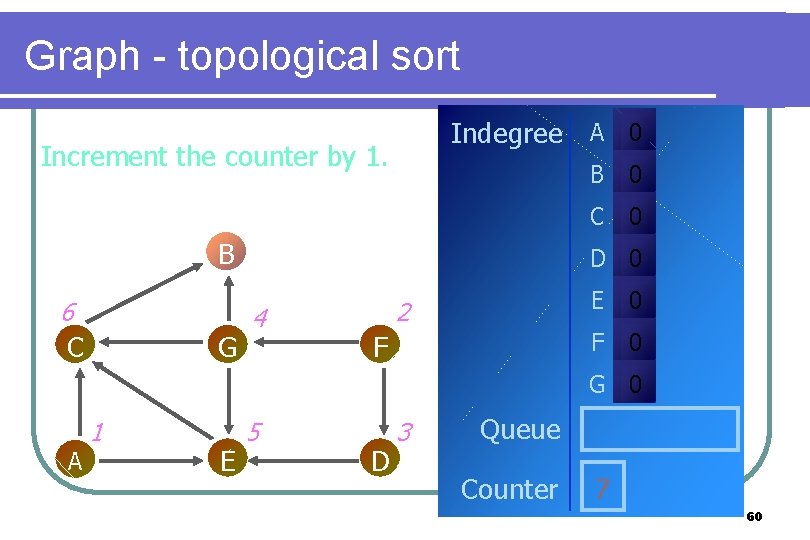
Graph - topological sort Indegree A 0 Increment the counter by 1. B 6 C G B 0 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 7 60
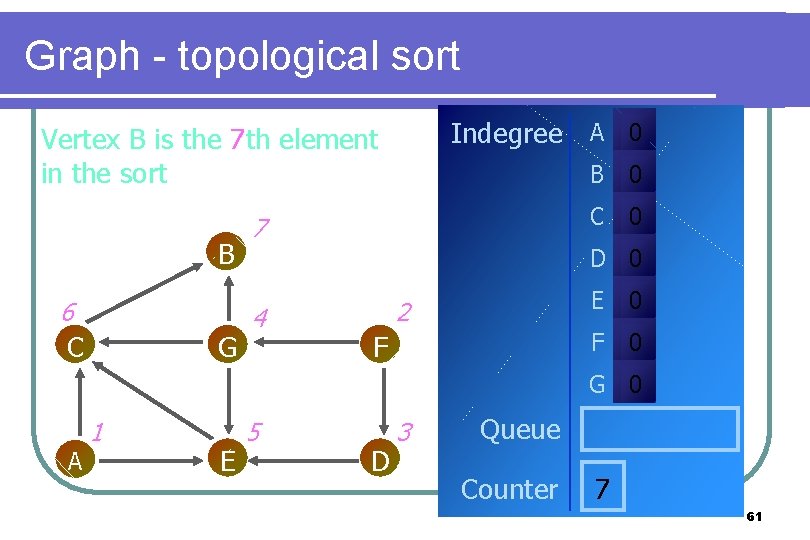
Graph - topological sort Indegree A 0 Vertex B is the 7 th element in the sort B 6 C G 7 B 0 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 7 61
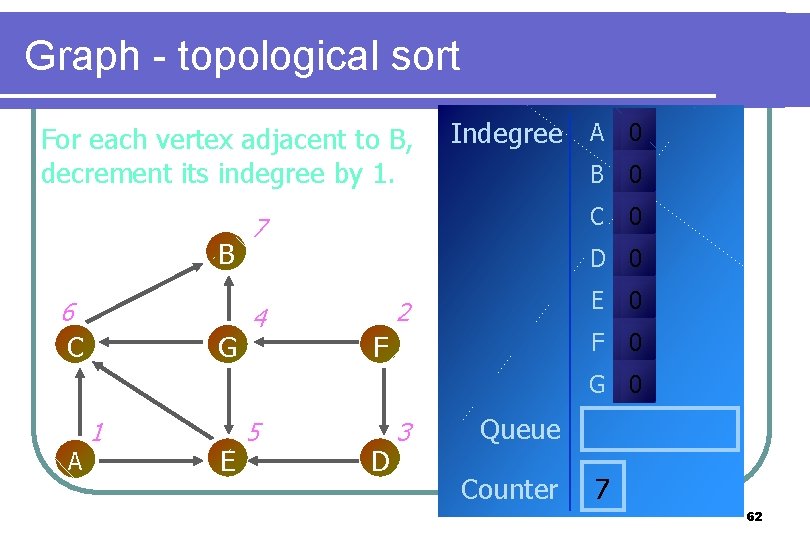
Graph - topological sort For each vertex adjacent to B, decrement its indegree by 1. B 6 C G Indegree A 0 7 B 0 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 7 62
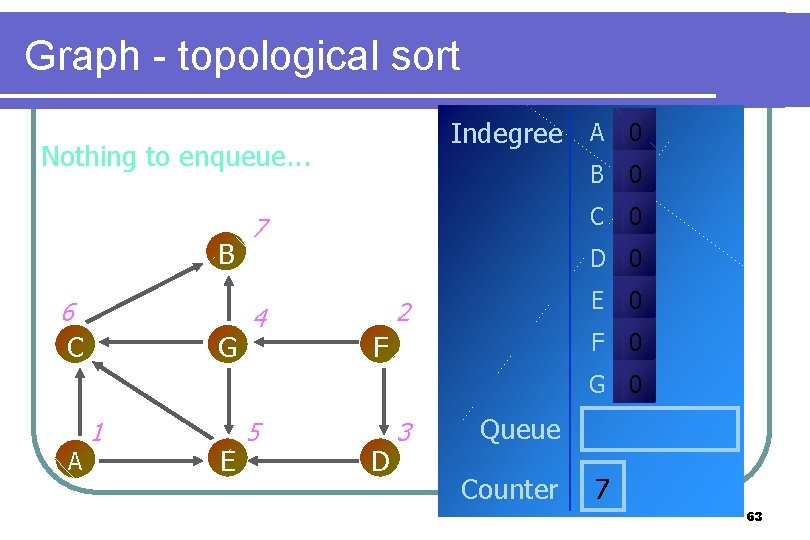
Graph - topological sort Indegree A 0 Nothing to enqueue. . . B 6 C G 7 B 0 C 0 D 0 4 2 F E 0 F 0 G 0 A 1 E 5 D 3 Queue Counter 7 63
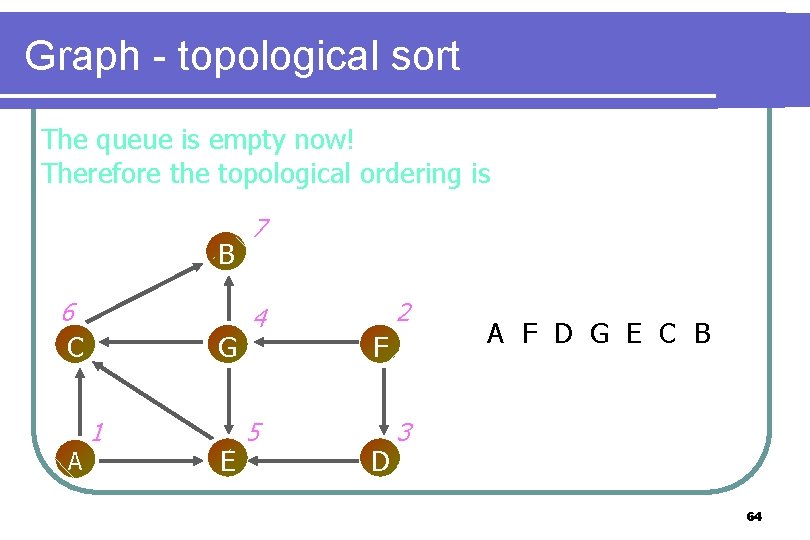
Graph - topological sort The queue is empty now! Therefore the topological ordering is B 6 C A G 1 E 7 4 5 2 F D A F D G E C B 3 64

Graph – single source shortest path l Dijkstra’s algorithm For non-negative weighted graph !!! l For each vertex, we have three variables l A boolean called Known l An integer dv for storing the shortest distance from s l A variable called pv for tracing the shortest path l 65

Graph - shortest path for ( ; ; ) { a = vertex with smallest unknown dv if (no such a) break; T[a]. Known = true; for each b adjacent to a if (T[b]. Known == false) if (T[a]. dv + (distance between a & b) < T[b]. dv) { T[b]. dv = T[a]. dv + (distance between a & b); T[b]. pv = a; } } 66
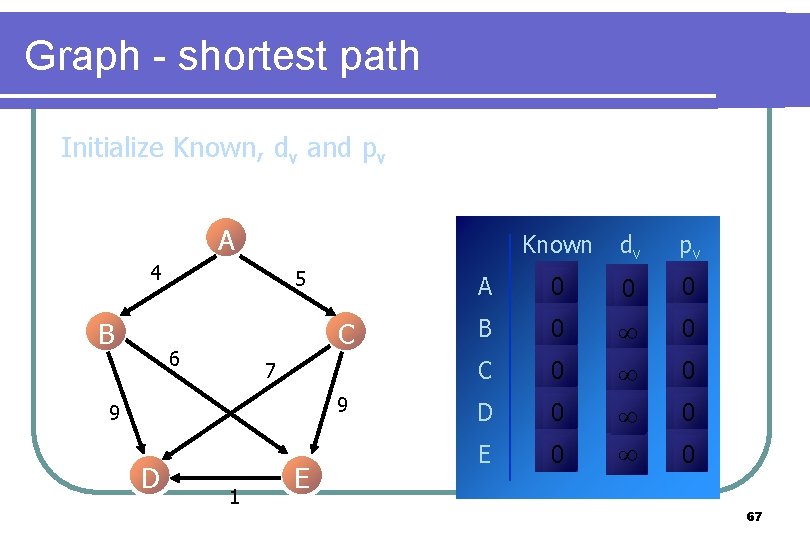
Graph - shortest path Initialize Known, dv and pv A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 0 0 0 B 0 0 C 0 D 0 E 0 0 0 0 67
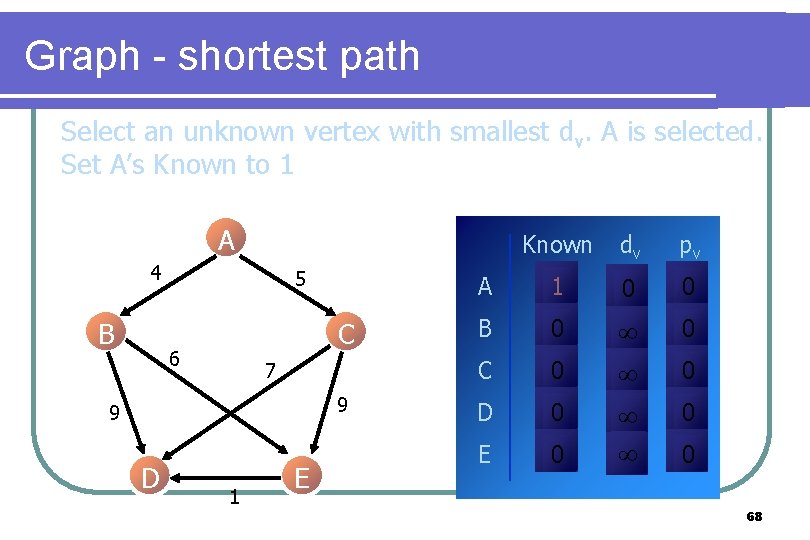
Graph - shortest path Select an unknown vertex with smallest dv. A is selected. Set A’s Known to 1 A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 1 0 0 B 0 0 C 0 D 0 E 0 0 0 0 68
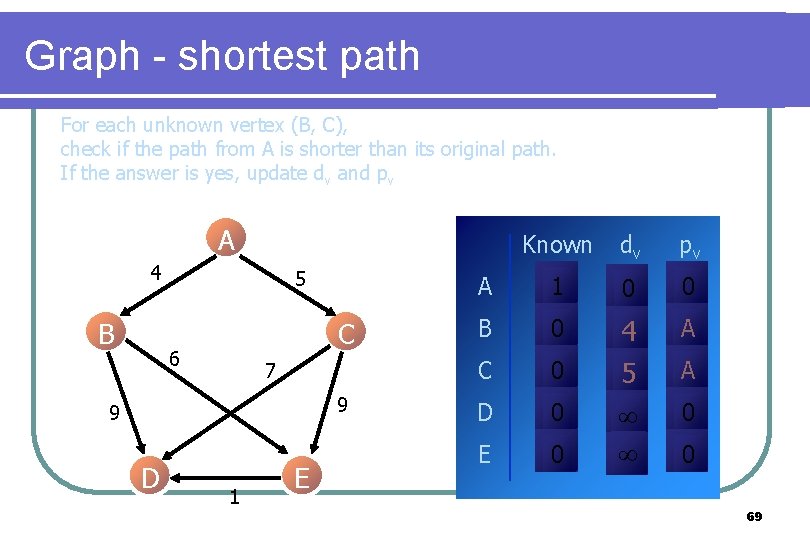
Graph - shortest path For each unknown vertex (B, C), check if the path from A is shorter than its original path. If the answer is yes, update dv and pv A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 1 0 0 B 0 A C 0 D 0 E 0 4 5 A 0 0 69
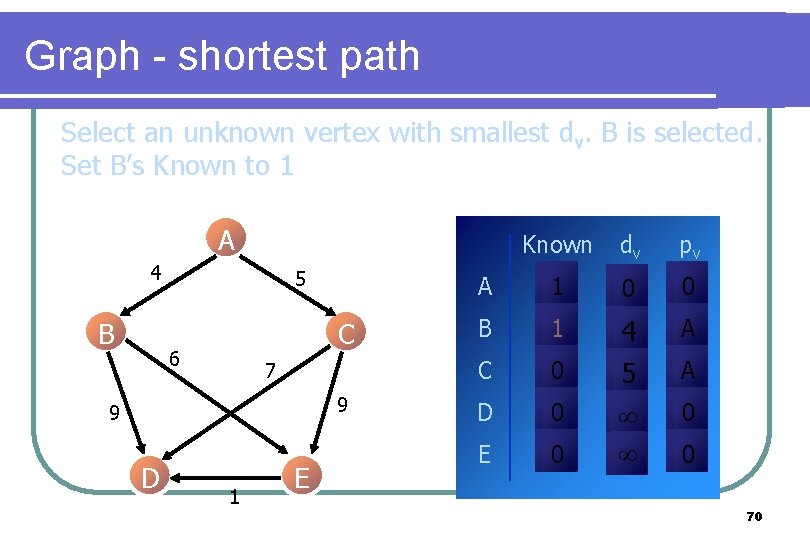
Graph - shortest path Select an unknown vertex with smallest dv. B is selected. Set B’s Known to 1 A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 1 0 0 B 1 A C 0 D 0 E 0 4 5 A 0 0 70
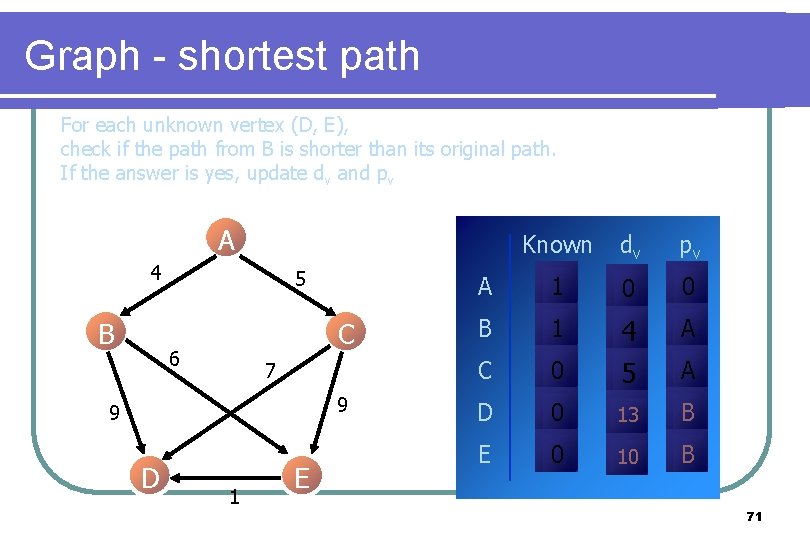
Graph - shortest path For each unknown vertex (D, E), check if the path from B is shorter than its original path. If the answer is yes, update dv and pv A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 1 0 0 B 1 A C 0 4 5 D 0 13 B E 0 10 B A 71
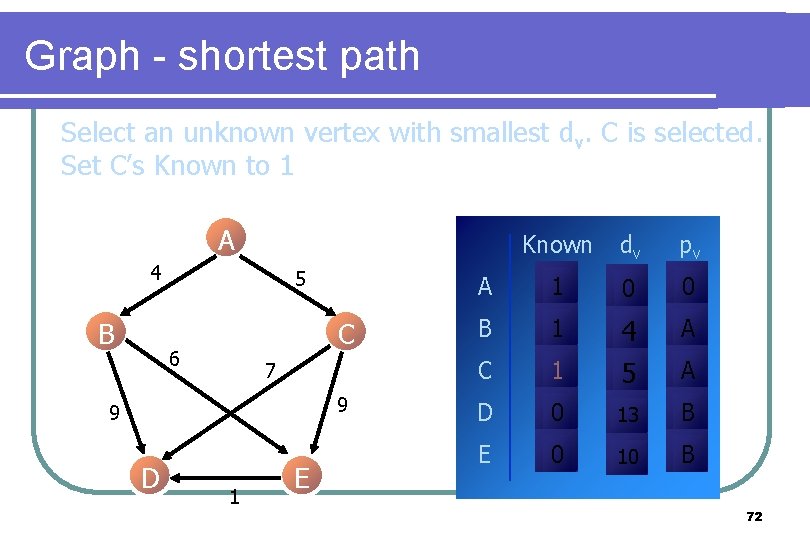
Graph - shortest path Select an unknown vertex with smallest dv. C is selected. Set C’s Known to 1 A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 1 0 0 B 1 A C 1 4 5 D 0 13 B E 0 10 B A 72
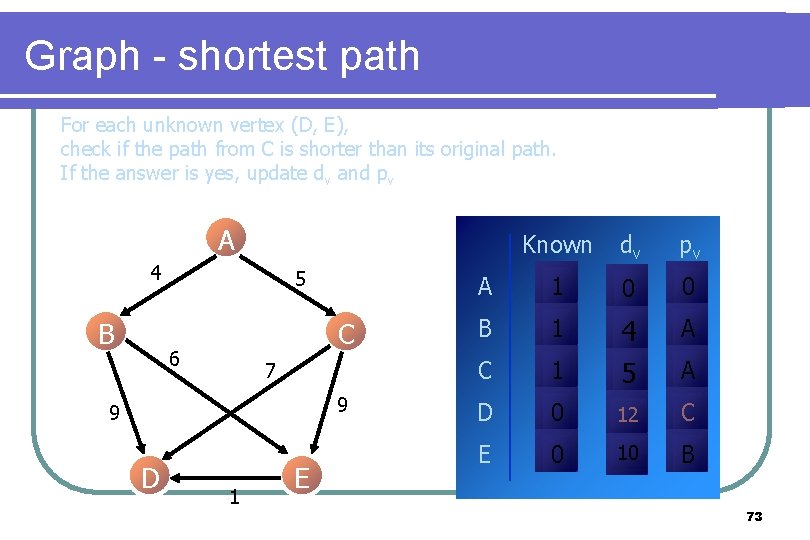
Graph - shortest path For each unknown vertex (D, E), check if the path from C is shorter than its original path. If the answer is yes, update dv and pv A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 1 0 0 B 1 A C 1 4 5 D 0 12 C E 0 10 B A 73
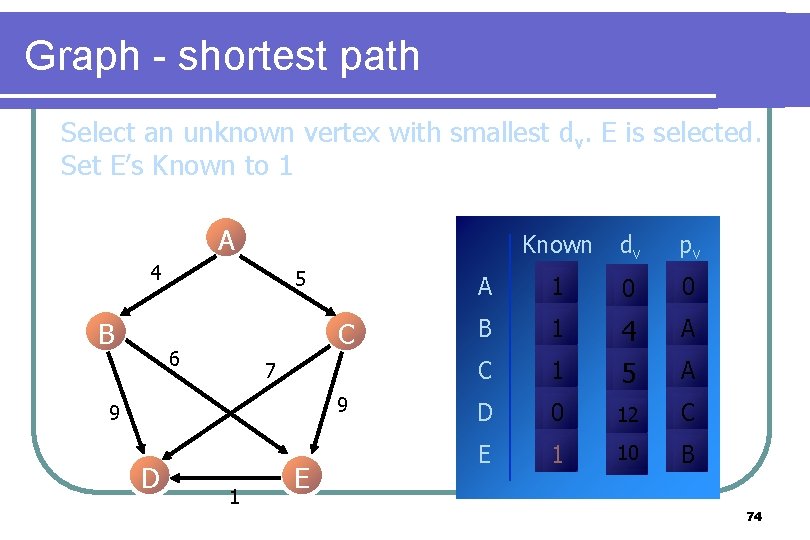
Graph - shortest path Select an unknown vertex with smallest dv. E is selected. Set E’s Known to 1 A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 1 0 0 B 1 A C 1 4 5 D 0 12 C E 1 10 B A 74
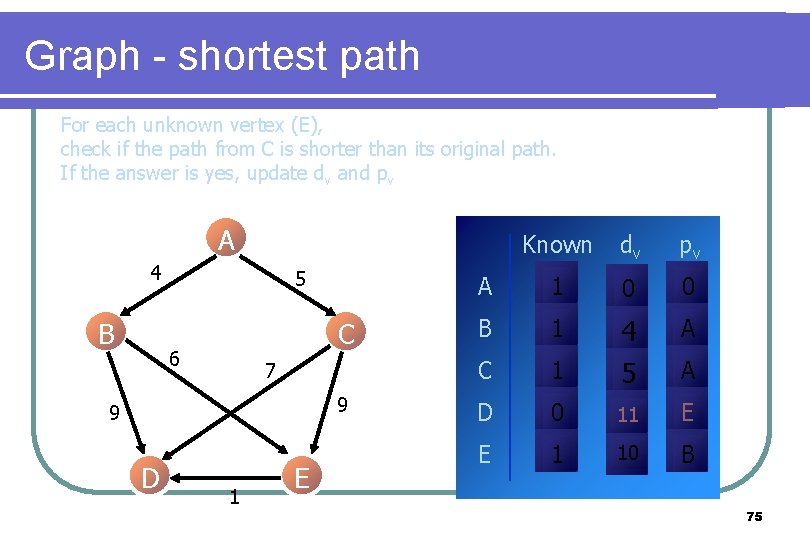
Graph - shortest path For each unknown vertex (E), check if the path from C is shorter than its original path. If the answer is yes, update dv and pv A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 1 0 0 B 1 A C 1 4 5 D 0 11 E E 1 10 B A 75
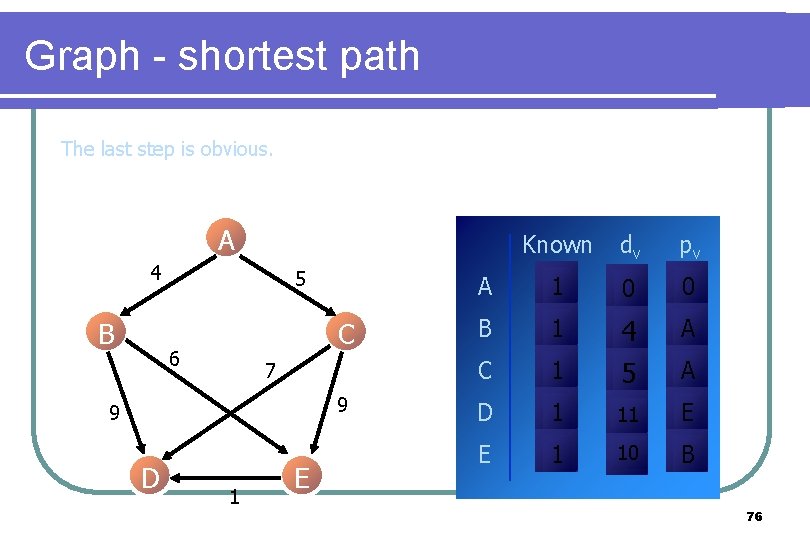
Graph - shortest path The last step is obvious. A 4 B 5 C 6 7 9 9 D 1 E Known dv pv A 1 0 0 B 1 A C 1 4 5 D 1 11 E E 1 10 B A 76
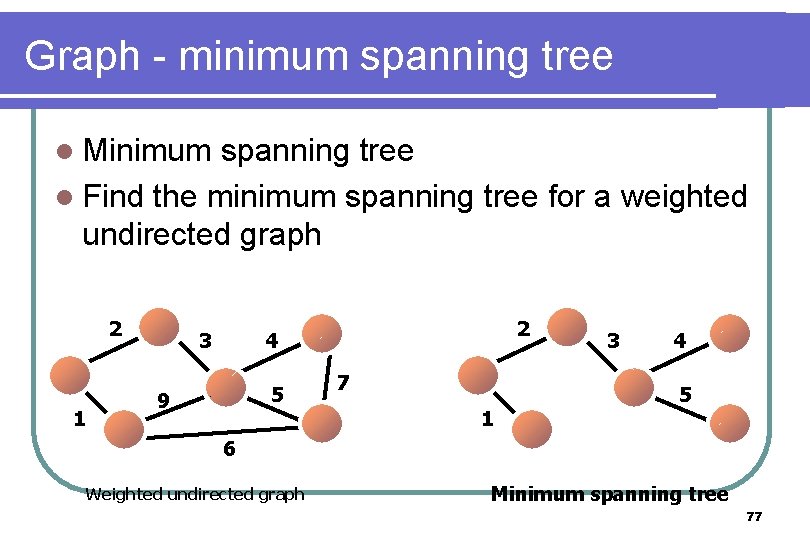
Graph - minimum spanning tree l Minimum spanning tree l Find the minimum spanning tree for a weighted undirected graph 2 1 3 2 4 5 9 7 1 3 4 5 6 Weighted undirected graph Minimum spanning tree 77

Graph - minimum spanning tree l Kruskal’s l algorithm Select the edges in order of smallest weight and accept an edge if it does not cause a cycle 78
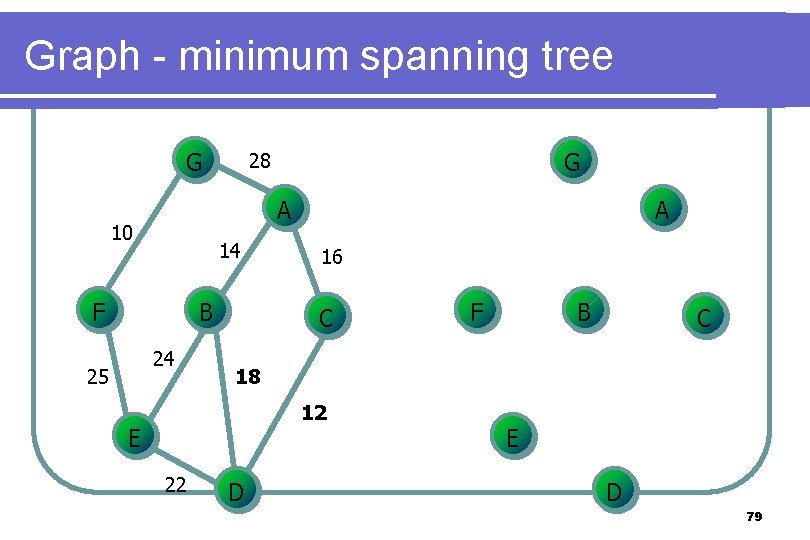
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 A 16 C B C 18 12 E 22 F D E D 79
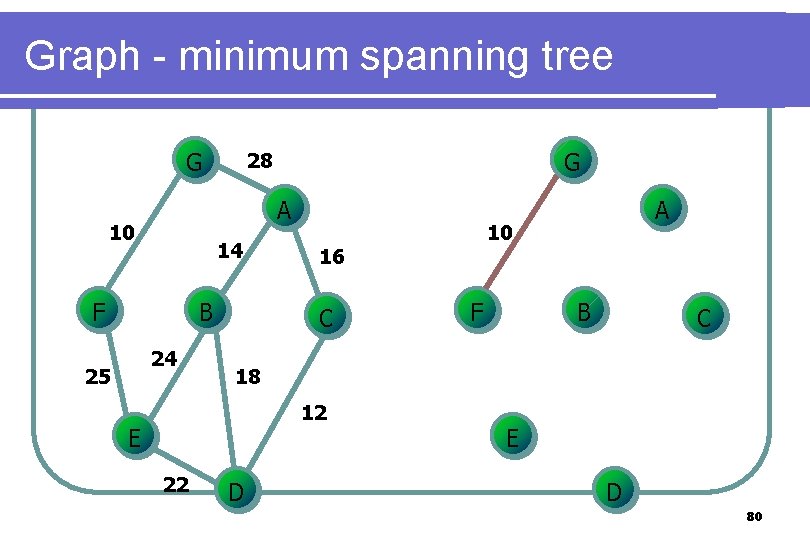
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 F B C 18 12 E 22 10 16 C A D E D 80
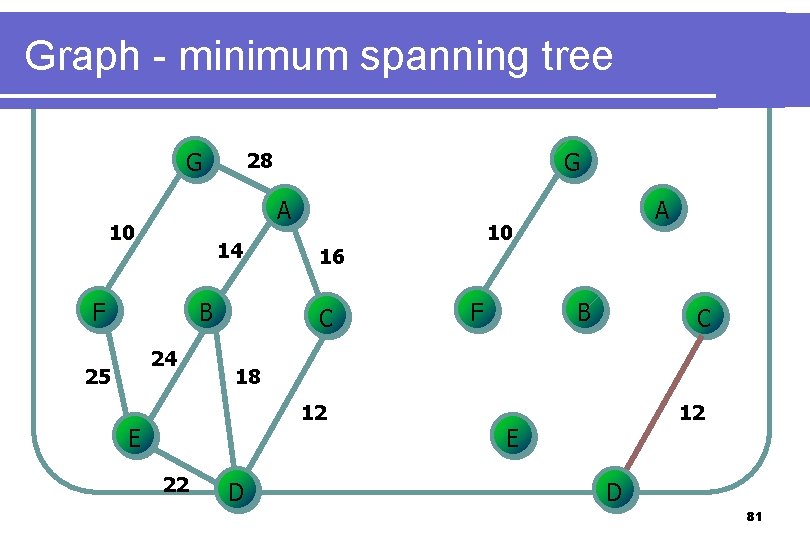
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 F B C 18 12 E 22 10 16 C A D 12 E D 81
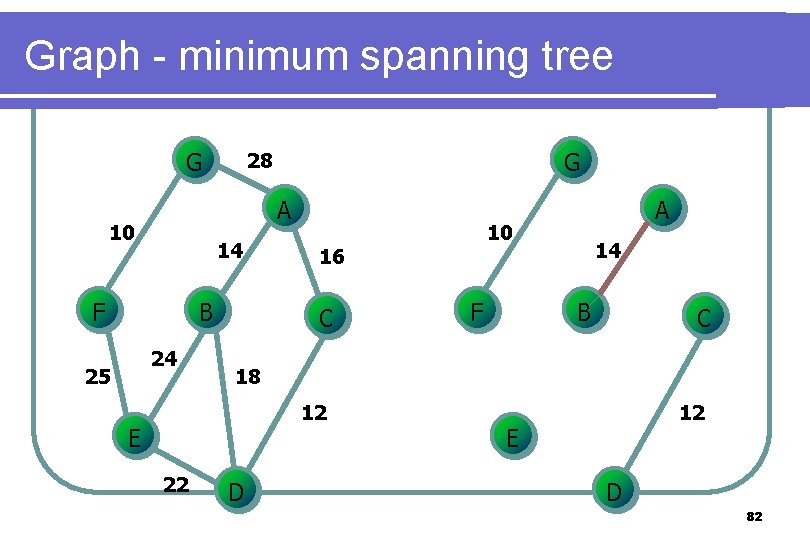
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 F 14 B C 18 12 E 22 10 16 C A D 12 E D 82
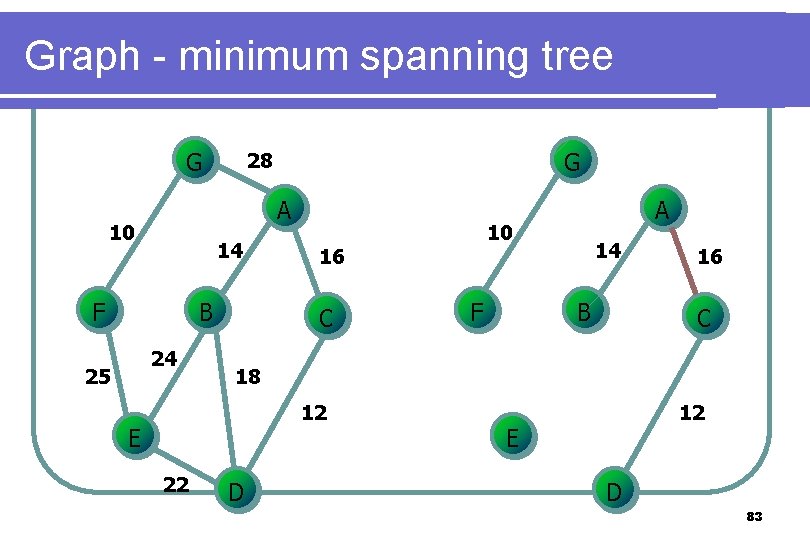
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 F 14 B 16 C 18 12 E 22 10 16 C A D 12 E D 83
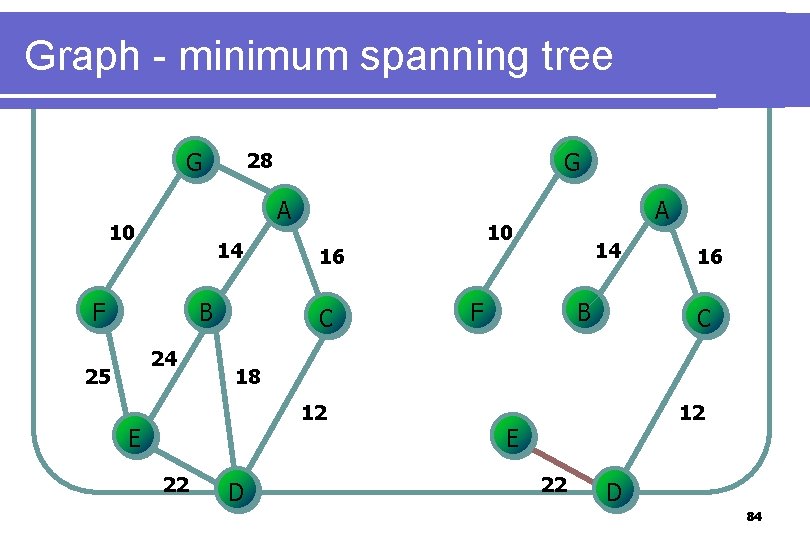
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 14 F B 16 C 18 12 E 22 10 16 C A D 12 E 22 D 84
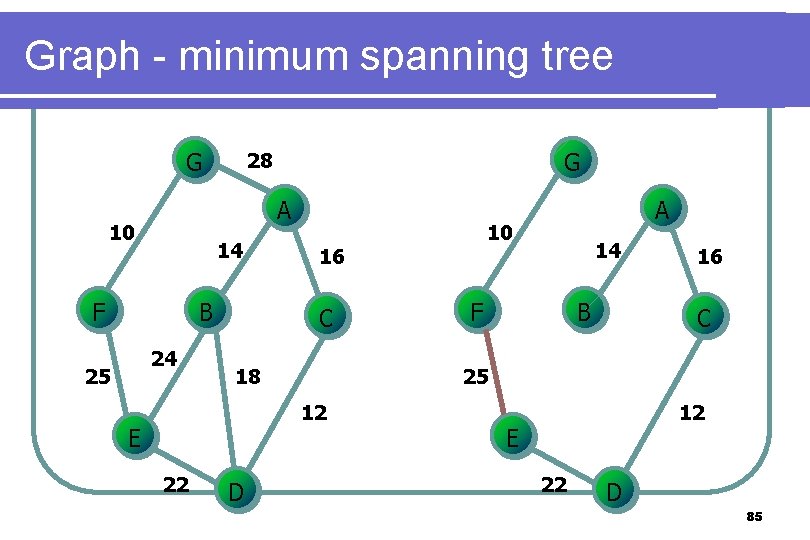
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 18 22 D 14 F B 16 C 25 12 E 10 16 C A 12 E 22 D 85

Graph - minimum spanning tree l Prim’s algorithm Grow the tree in successive stages l At each stage, a new vertex is added to the tree by choosing the edge (u, v) such that the cost of (u, v) is the smallest among all edges where u is in the tree and v is not. l 86
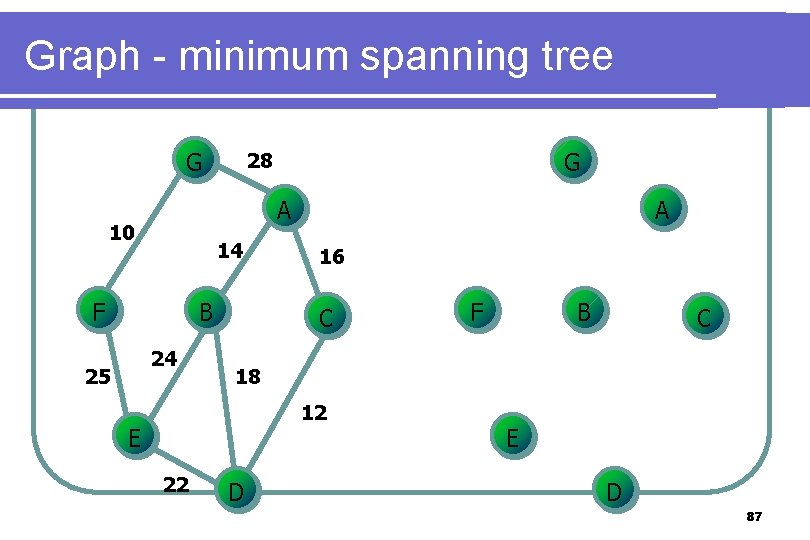
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 A 16 C B C 18 12 E 22 F D E D 87
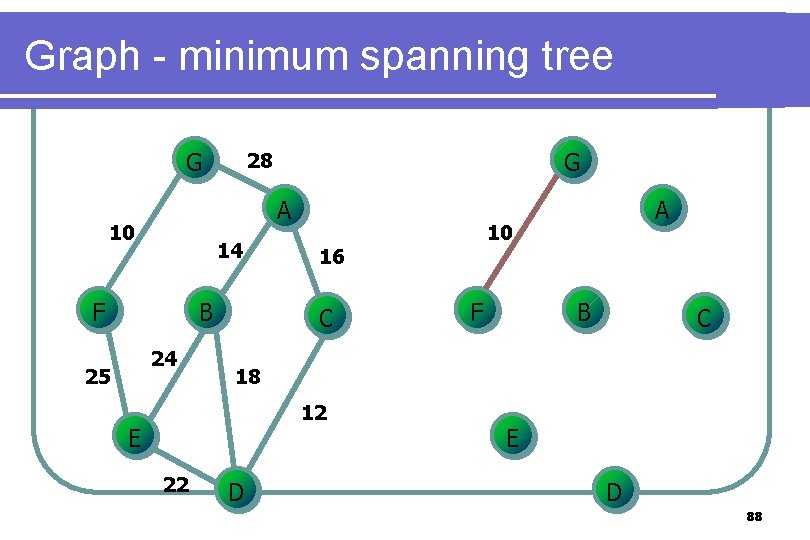
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 F B C 18 12 E 22 10 16 C A D E D 88
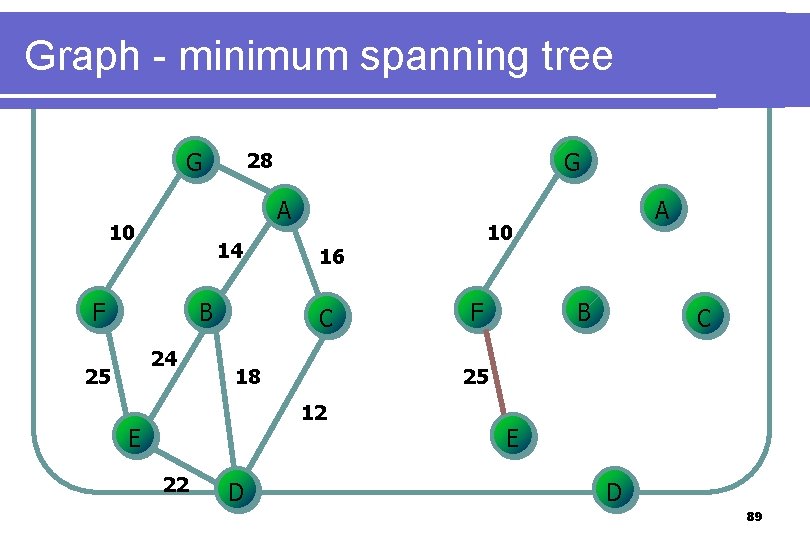
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 18 22 D F B C 25 12 E 10 16 C A E D 89
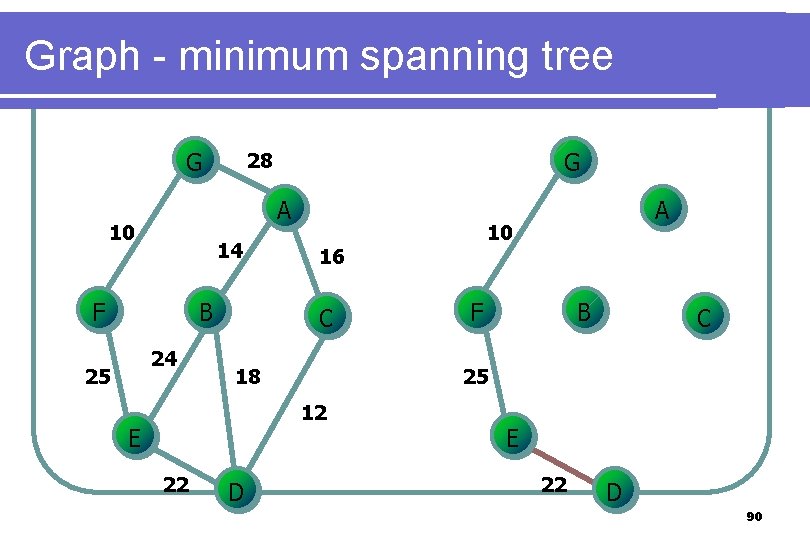
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 18 22 D F B C 25 12 E 10 16 C A E 22 D 90
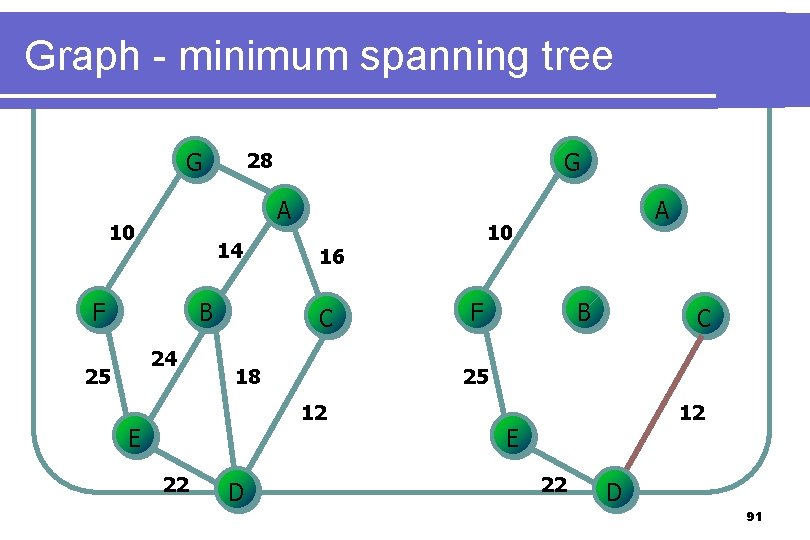
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 18 22 D F B C 25 12 E 10 16 C A 12 E 22 D 91
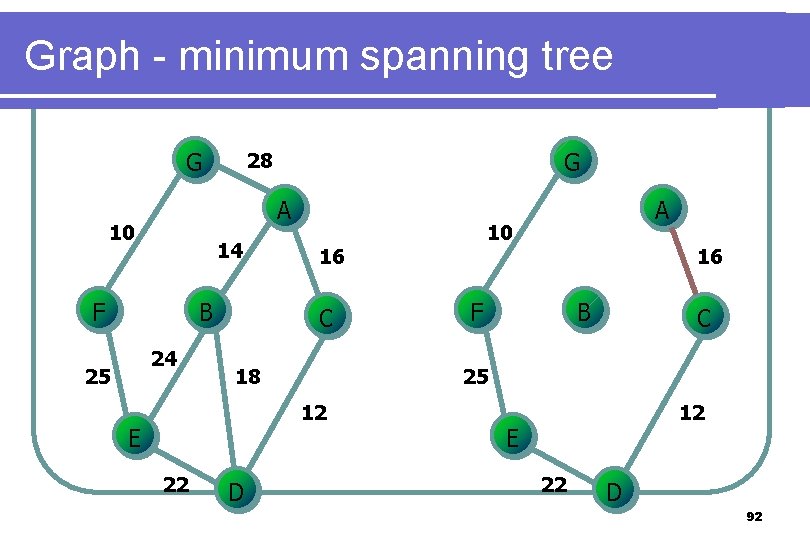
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 18 22 D 16 F B C 25 12 E 10 16 C A 12 E 22 D 92
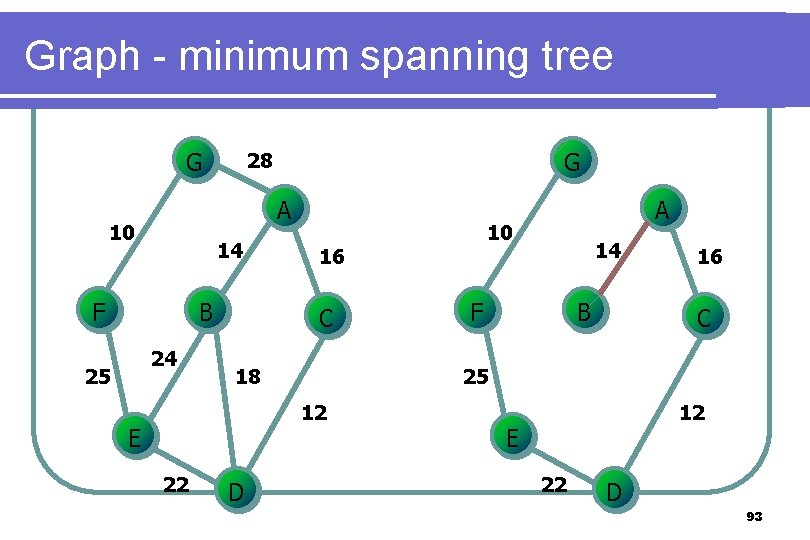
Graph - minimum spanning tree G A 10 14 F B 24 25 G 28 18 22 D 14 F B 16 C 25 12 E 10 16 C A 12 E 22 D 93
- Slides: 93