CSC 2100 B Tutorial 4 AVL Tree Hao

CSC 2100 B Tutorial 4 AVL Tree Hao Ma 1

Definition l An AVL tree (or Height-Balanced tree) is a binary search tree such that: l l The height of the left and right subtrees of the root differ by at most 1. The left and right subtrees of the root are AVL trees. 2

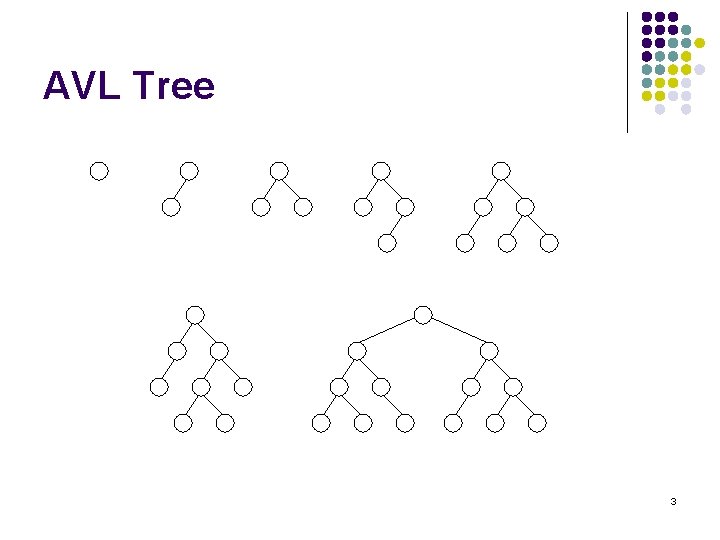
AVL Tree 3

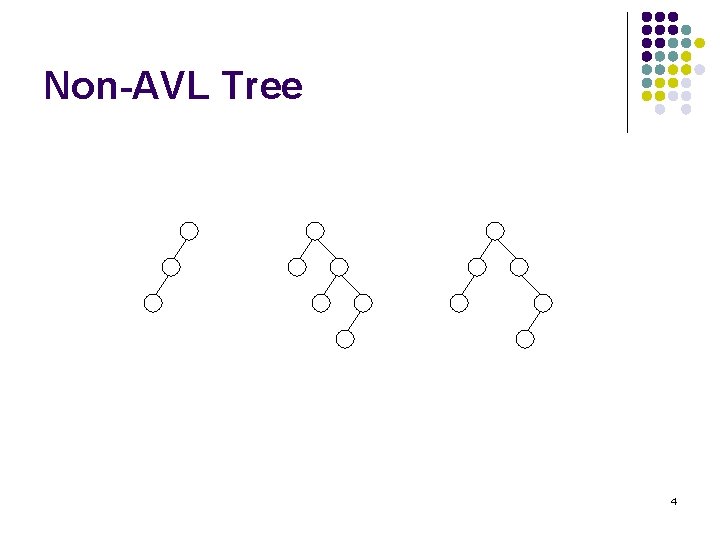
Non-AVL Tree 4

Balance Factor l To keep track of whether a binary search tree is a AVL tree, we associate with each node a balance factor, which is Height(right subtree) – Height(left subtree) 5

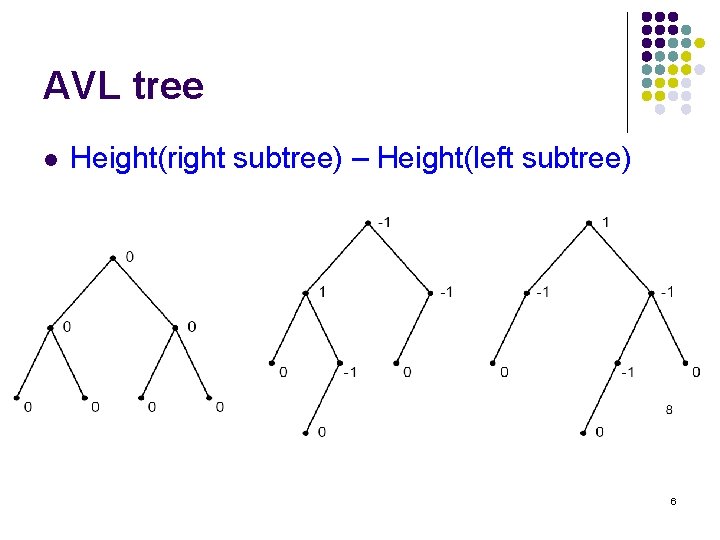
AVL tree l Height(right subtree) – Height(left subtree) 6

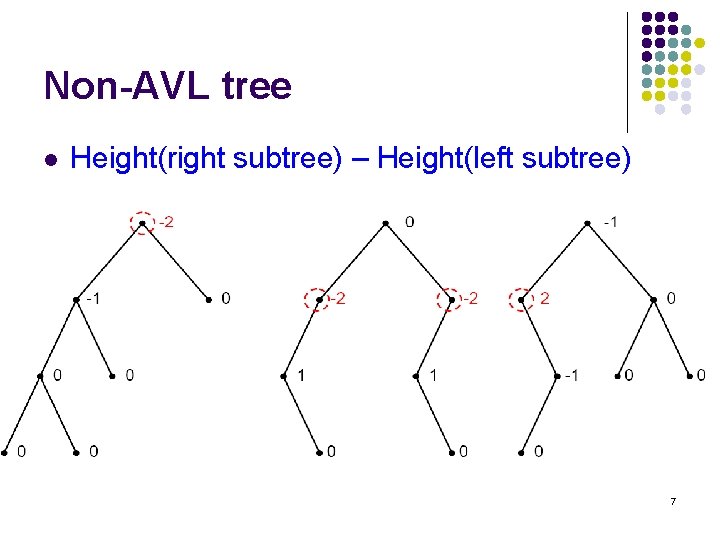
Non-AVL tree l Height(right subtree) – Height(left subtree) 7

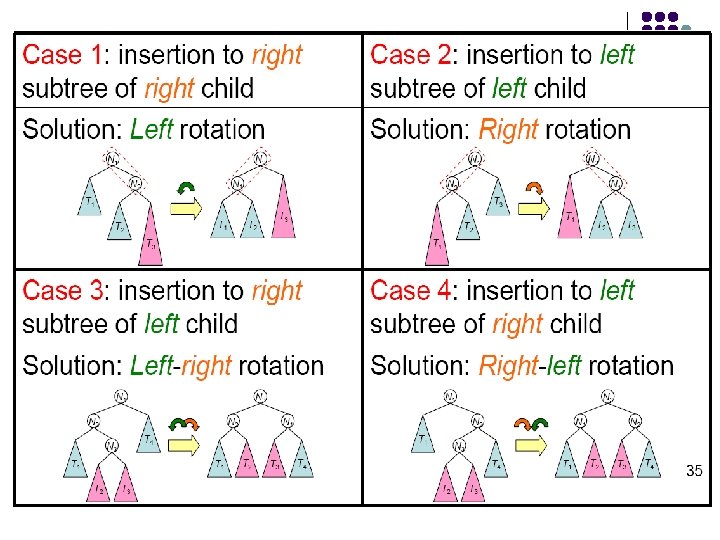
Imbalance l Insertions cause imbalances l Four types of imbalances are introduced. 8

9

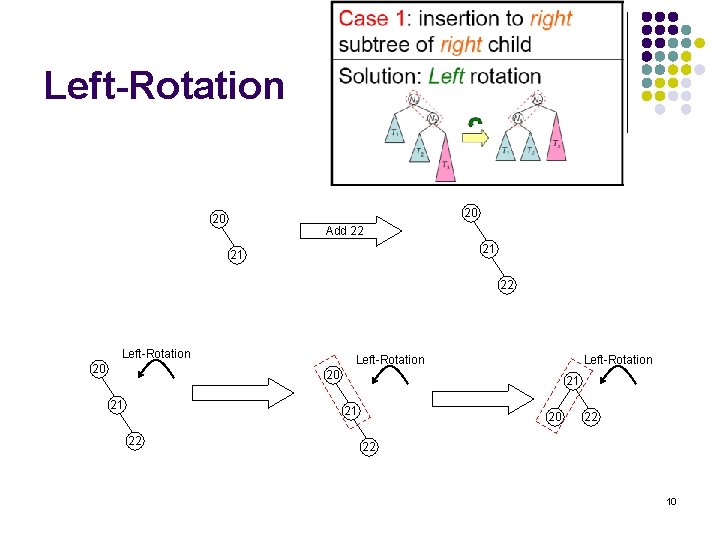
Left-Rotation 20 20 Add 22 21 21 22 Left-Rotation 20 21 21 21 22 20 22 22 10

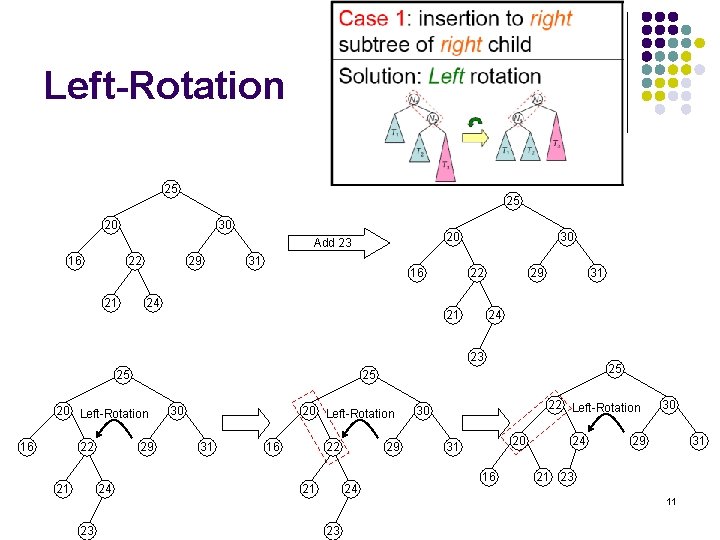
Left-Rotation 25 25 20 30 20 Add 23 16 22 21 29 31 16 24 30 22 21 29 31 24 23 25 20 Left-Rotation 16 22 21 29 24 25 25 30 20 Left-Rotation 31 16 22 21 29 24 22 Left-Rotation 30 20 31 16 24 30 29 31 21 23 11 23 23

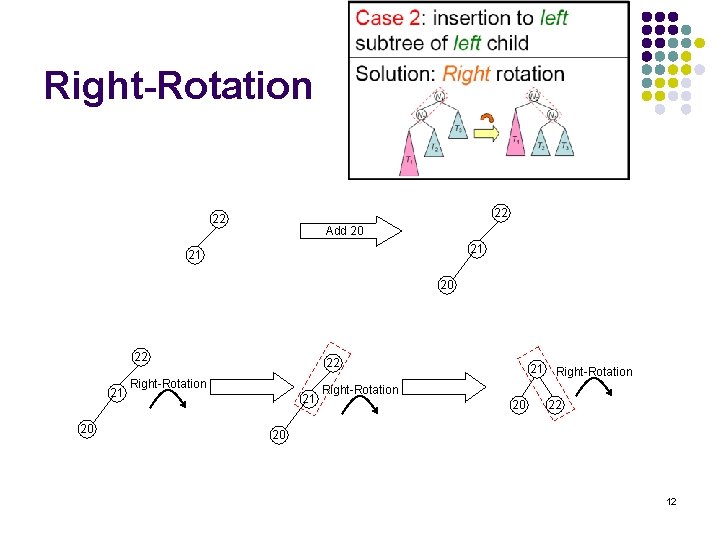
Right-Rotation 22 22 Add 20 21 21 20 22 Right-Rotation 21 21 Right-Rotation 20 22 20 12

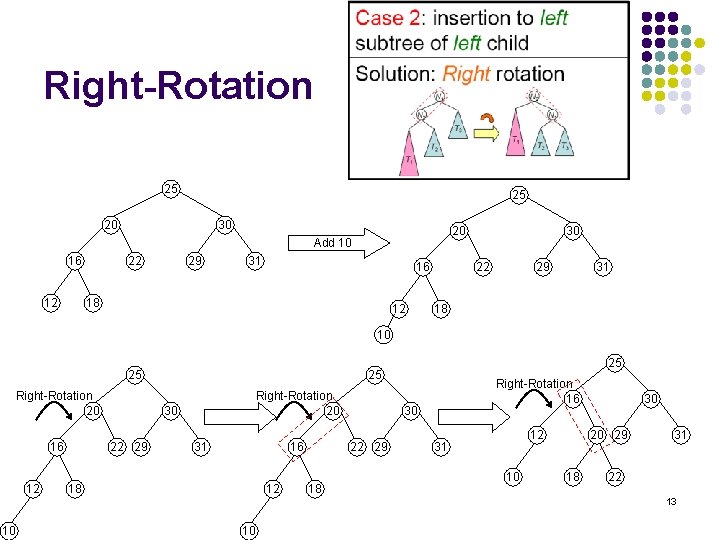
Right-Rotation 25 25 20 30 20 Add 10 16 12 22 29 31 16 18 12 30 22 29 31 18 10 25 Right-Rotation 20 16 12 Right-Rotation 20 30 22 29 25 25 31 16 18 12 30 22 29 18 Right-Rotation 16 12 31 10 30 20 29 18 31 22 13 10 10

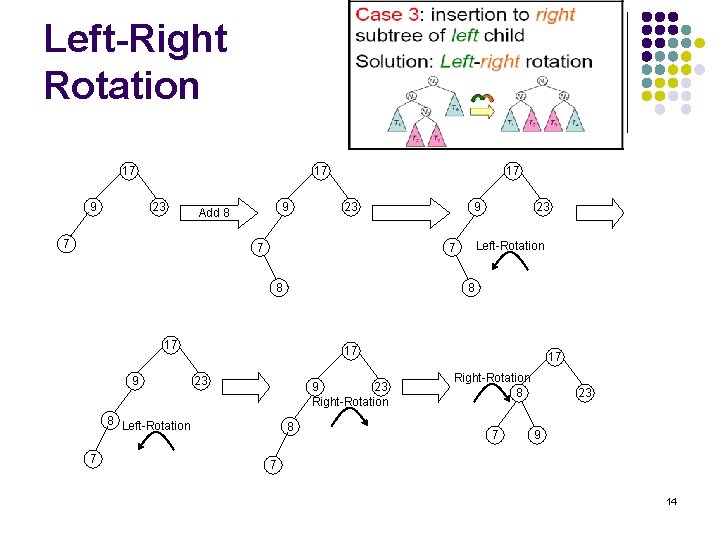
Left-Right Rotation 17 9 17 23 9 Add 8 7 17 23 7 8 17 17 23 9 23 Right-Rotation 8 Left-Rotation 7 23 Left-Rotation 7 8 9 9 8 17 Right-Rotation 8 7 23 9 7 14

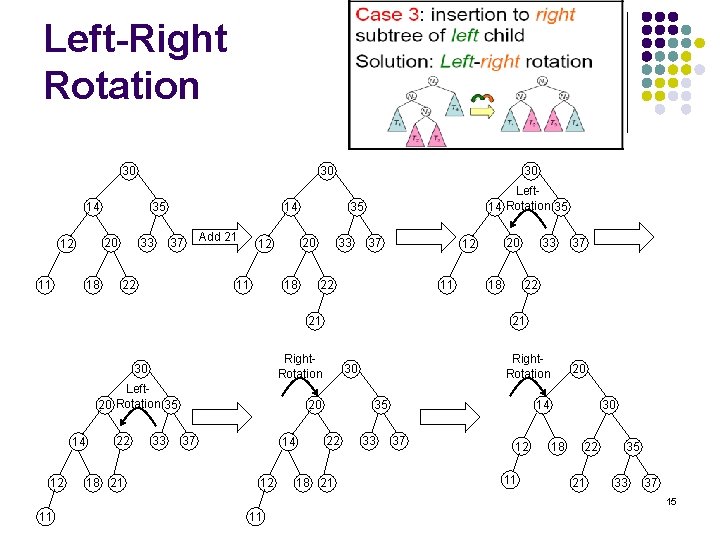
Left-Right Rotation 30 30 14 20 12 11 35 18 33 30 14 37 22 Add 21 11 35 20 12 18 Left 14 Rotation 35 33 37 22 11 21 Left. Rotation 20 35 14 12 22 18 21 33 14 12 37 22 Right. Rotation 30 20 37 18 33 21 Right. Rotation 30 20 12 35 22 18 21 33 20 14 37 12 11 30 18 22 21 35 33 37 15 11 11

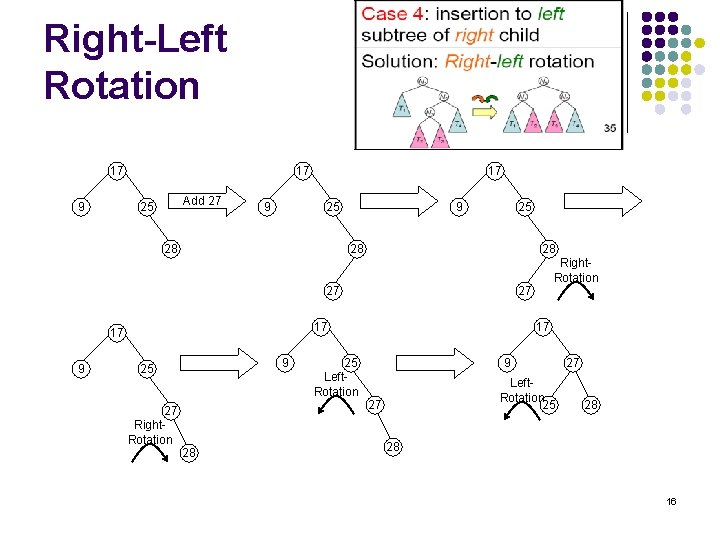
Right-Left Rotation 17 9 17 Add 27 25 9 17 25 28 9 25 28 28 Right. Rotation 27 17 17 9 25 17 25 Left. Rotation 9 Left. Rotation 25 27 27 Right. Rotation 28 27 28 28 16

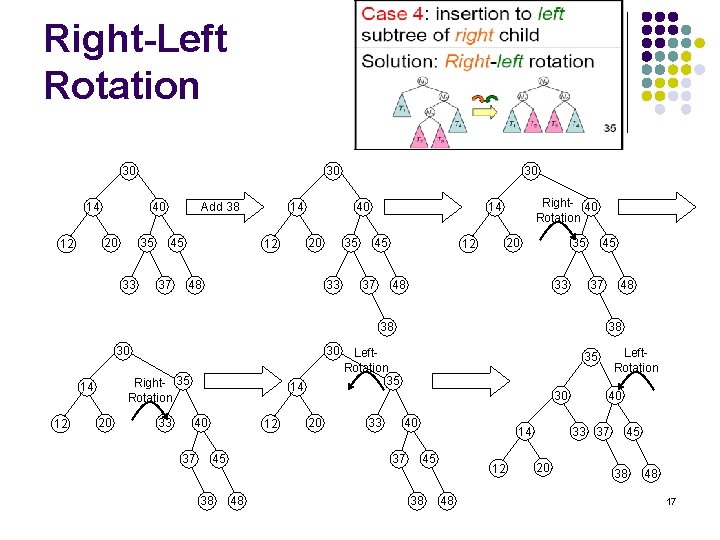
Right-Left Rotation 30 14 40 20 12 30 35 33 14 Add 38 45 37 40 20 12 30 48 35 33 Right- 40 Rotation 14 45 37 20 12 35 48 33 45 37 38 30 Right- 35 Rotation 14 12 30 20 33 14 40 37 12 45 38 38 Left. Rotation 35 33 40 37 48 Left. Rotation 35 30 20 48 14 45 38 12 48 40 33 37 20 45 38 48 17

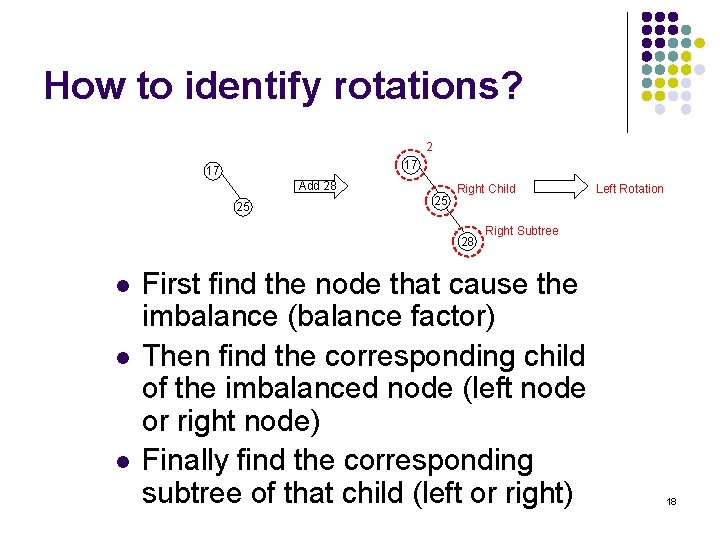
How to identify rotations? 2 17 17 Add 28 25 25 Right Child 28 l l l Left Rotation Right Subtree First find the node that cause the imbalance (balance factor) Then find the corresponding child of the imbalanced node (left node or right node) Finally find the corresponding subtree of that child (left or right) 18

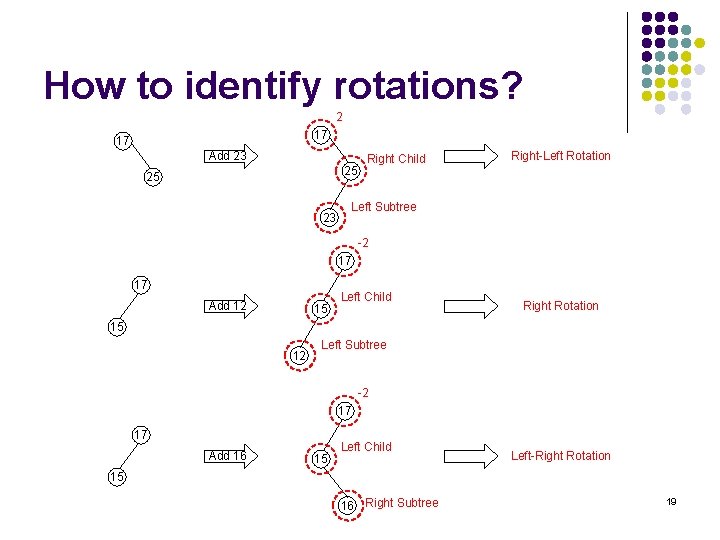
How to identify rotations? 2 17 17 Add 23 25 25 23 Right Child Right-Left Rotation Left Subtree -2 17 17 Add 12 15 Left Child Right Rotation 15 12 Left Subtree -2 17 17 Add 16 15 Left Child Left-Right Rotation 15 16 Right Subtree 19

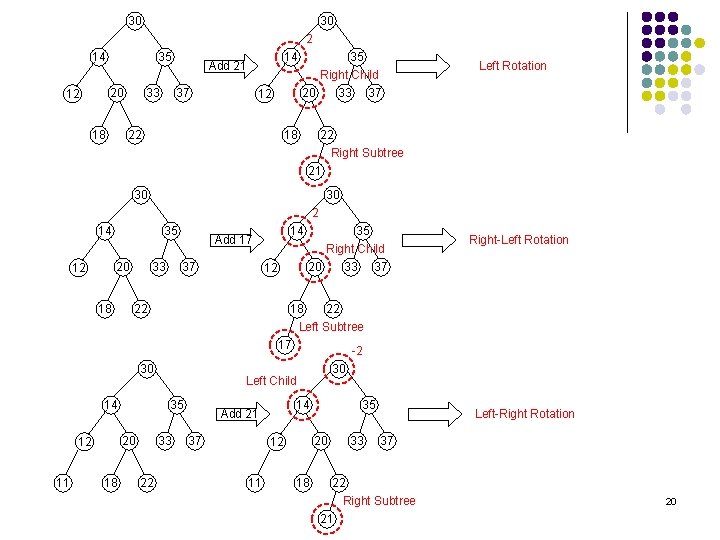
30 30 2 14 35 20 12 18 33 14 Add 21 37 35 Right Child 20 33 37 12 22 18 Left Rotation 22 Right Subtree 21 30 30 2 14 35 20 12 18 33 14 Add 17 37 35 Right Child 20 33 37 12 22 18 Right-Left Rotation 22 Left Subtree 17 30 14 11 18 33 22 30 Left Child 35 20 12 -2 14 Add 21 37 20 12 11 35 18 33 Left-Right Rotation 37 22 Right Subtree 21 20

Useful Tool l A useful tool to help you understand AVL tree http: //www. site. uottawa. ca/~stan/csi 2514/appl ets/avl/BT. html 21

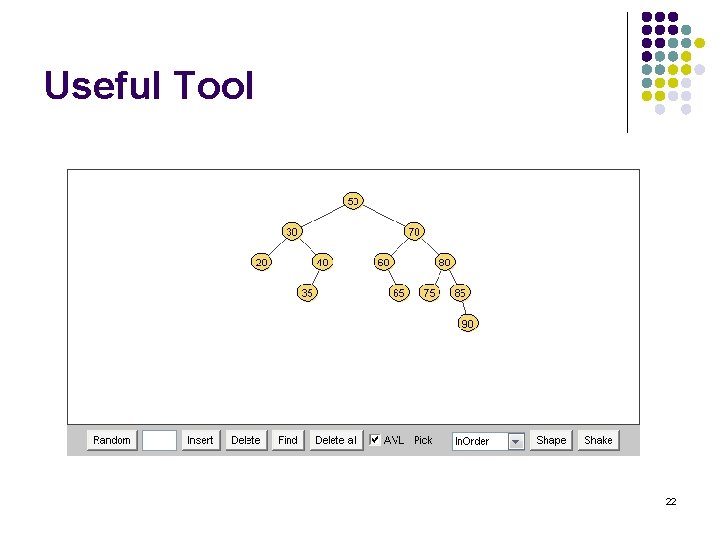
Useful Tool 22

l l l You can insert, delete and locate nodes in the tree using control buttons. The data can be entered manually or randomly generated. By pressing <Insert> button only, you can quickly build a large tree. 23

Demo http: //www. site. uottawa. ca/~stan/csi 2514/appl ets/avl/BT. html 24

The End Any Questions? 25