CSC 1800 Organization of Programming Languages Syntax Questions

CSC 1800 Organization of Programming Languages Syntax

Questions l What is a computer program? l What is a programming language? l Describe the alphabet available to you to create programs 2

Programs, formally l l Let A be the alphabet of a programming language L, hence a subset of all the keyboard-producible characters. Let A* be the set of finite sequences of characters of A. L is a subset of A*. That is, any program P in L is a sequence of characters in A. Why is this definition not completely correct? 3

Syntax l The description of a language specifying structurally correct phrases in the language. As opposed to l Semantics – The meaning of phrases in the language 4

Syntax (2) and l Pragmatics – – – The practical use of the language Communicating algorithms to humans Laying out a program in readable form Purpose of the language User interface to the language including IDE Efficiency of generated code 5

Simple Syntax <letter> : : = a|b|c|d|e|f|g|h|i|j|k|l|m|n|o|p| q|r|s|t|u|v|w|x|y|z Non-terminal: <letter> Terminals: lower case letters (26 choices) | means “or” 6

Simple Syntax (2) <letter seq> : : = <letter> | <letter seq><letter> Notes: l Right recursion (or is it left recursion? ) l Does the recursive order make a difference? l What are permissible lengths of letter sequences? 7

Simple Syntax (3) <digit> : : = 0|1|2|3|4|5|6|7|8|9 <digit string> : : = <digit> | <digit string><digit> Your turn: l Create the syntax specification for an integer 8

BNF l Backus-Naur Form (or Backus Normal Form) – – – l Use for – – l John Backus, developer of Fortran Peter Naur Revised Report on the Algorithmic Language Algol 60, Computer Journal, 5(1963), 349 -367. Checking a symbol string for syntactic correctness Generating a correct symbol string The examples on the previous slide use BNF 9

BNF : : = | < > is defined as or syntactic category, grammatical category 10

Extended BNF For those who dislike recursion: l l l [ ] surround an optional part { } surround a repeated part, repeated 0 or more times ( ) are used to clarify hierarchy 11

Sequences In many instances, we need to specify a sequence of items. This may be done recursively: <seq> : : = <id> | <seq> , <id> or <seq> : : = <id> | <id> , <seq> or (using EBNF) <seq> : : = <id> { , <id> } 12

Context Free Grammar l Defined with four (4) elements: – terminal symbols l l – non-terminal symbols l – each specifies a grammatical category, syntactic category, or set of strings of terminal symbols special non-terminal, the start symbol l – formed as strings of the alphabet of the language lexical elements of the language appears only on LHS of a productions l recursively defines all non-terminal symbols by showing how terminal and non-terminal symbols may be combined 13

Context Free Language l l Defined by a context free grammar The set of all strings of terminal symbols generated by the context free grammar 14

Parse Tree l l A labeled rooted tree Root labeled with start symbol Interior nodes labeled with non-terminal symbols (syntactic categories) Leaves labeled with terminal symbols 15

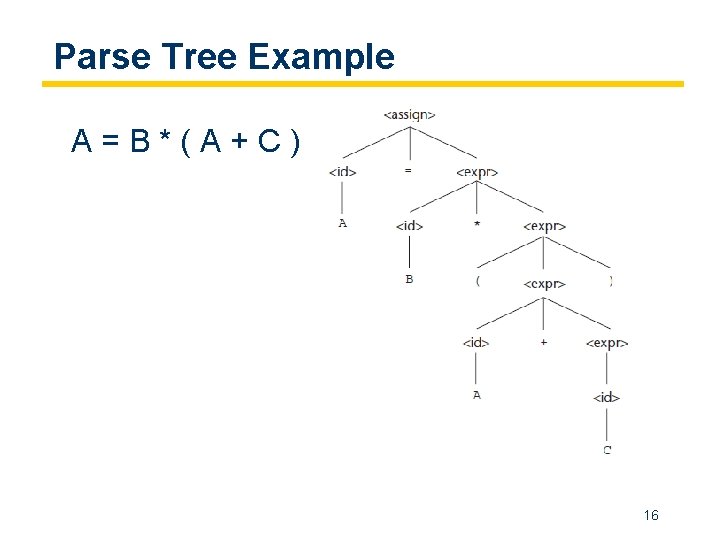
Parse Tree Example A=B*(A+C) 16

Grammar of Expressions Using a simplified EBNF S : : = E E : : = T | E + T | E – T T : : = F | T*F | T/F F : : = (E) | I | N Key: S – statement E – expression T – term F – factor I – identifier N – number What is this language? 17

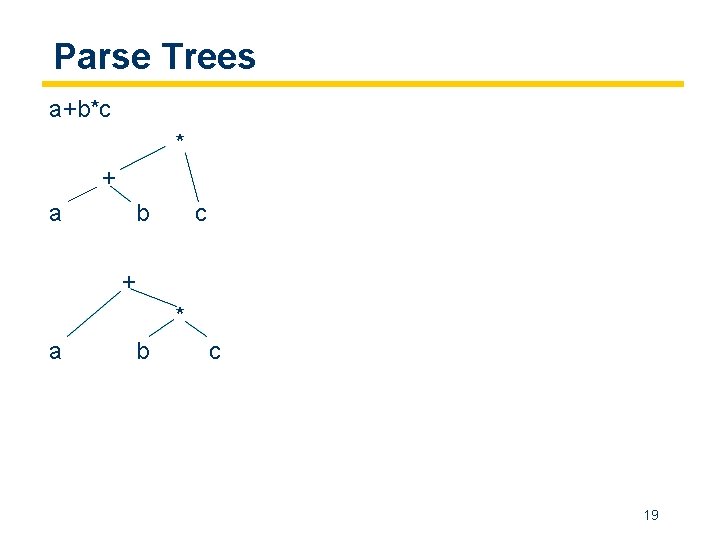
Expression Parse Trees Your turn: 1. 2. Build a parse tree for a+b*c Build a parse tree for a-b-c Infer rules for associativity and distributivity from the structure of the grammar. [Note: example trees on next slide… no peeking] 18

Parse Trees a+b*c * + a b c + * a b c 19

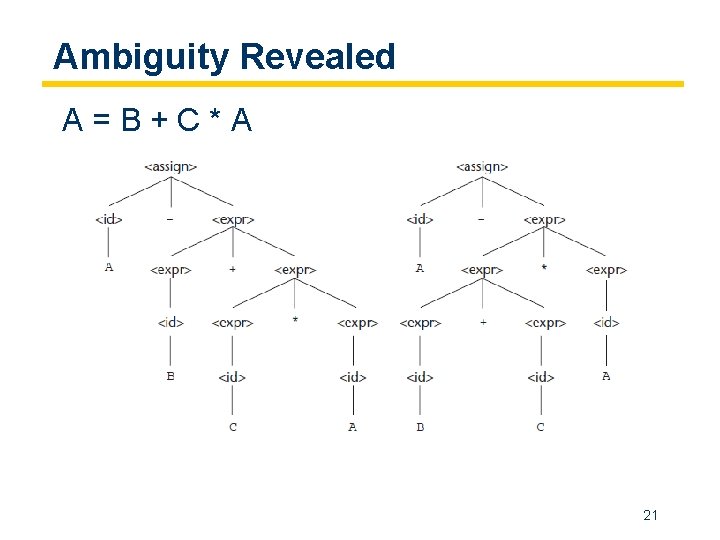
Ambiguity Some grammars lead to distinct parse trees for the same expression. Questions: 1. What does distinct mean? 2. Is this situation bad? 3. What can be done? 20

Ambiguity Revealed A=B+C*A 21