CS U 540 Computer Graphics Prof Harriet Fell

CS U 540 Computer Graphics Prof. Harriet Fell Spring 2007 Lecture 11 – February 1, 2007 ©College of Computer and Information Science, Northeastern University 1

Today’s Topics • Linear Algebra Review § Matrices § Transformations • New Linear Algebra § Homogeneous Coordinates ©College of Computer and Information Science, Northeastern University 2

Matrices • We use 2 x 2, 3 x 3, and 4 x 4 matrices in computer graphics. • We’ll start with a review of 2 D matrices and transformations. ©College of Computer and Information Science, Northeastern University 3

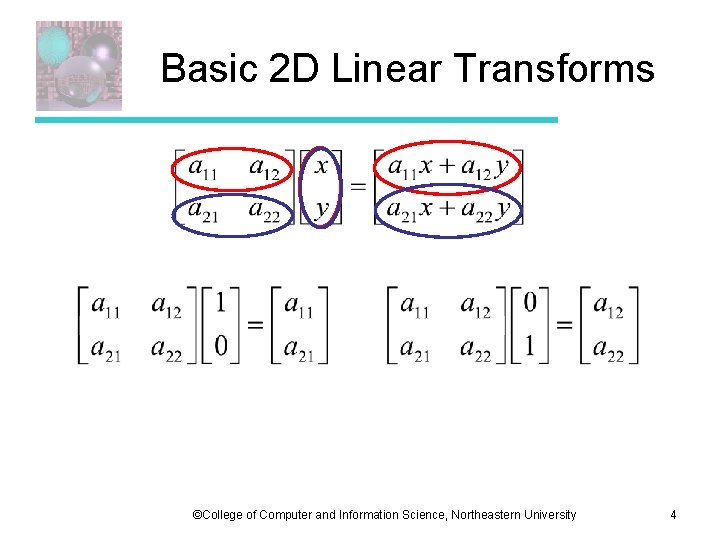
Basic 2 D Linear Transforms ©College of Computer and Information Science, Northeastern University 4

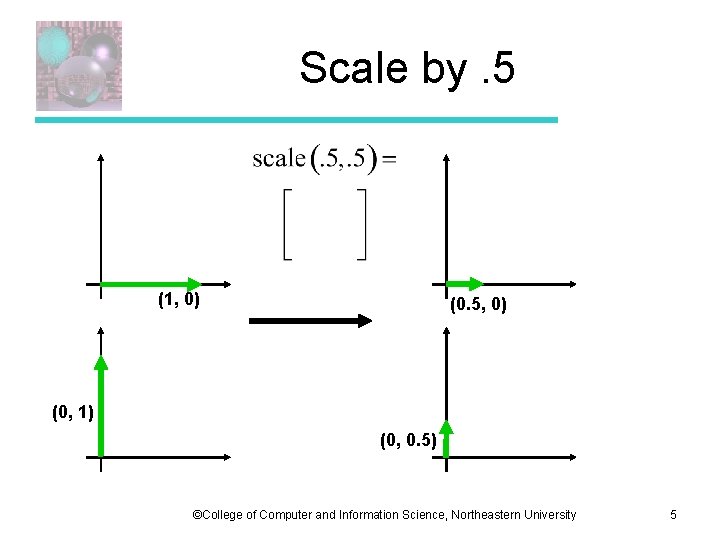
Scale by. 5 (1, 0) (0. 5, 0) (0, 1) (0, 0. 5) ©College of Computer and Information Science, Northeastern University 5

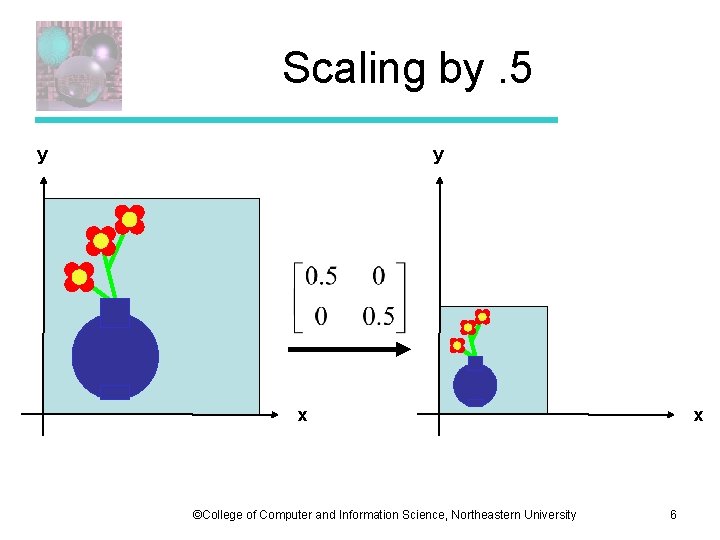
Scaling by. 5 y y x ©College of Computer and Information Science, Northeastern University x 6

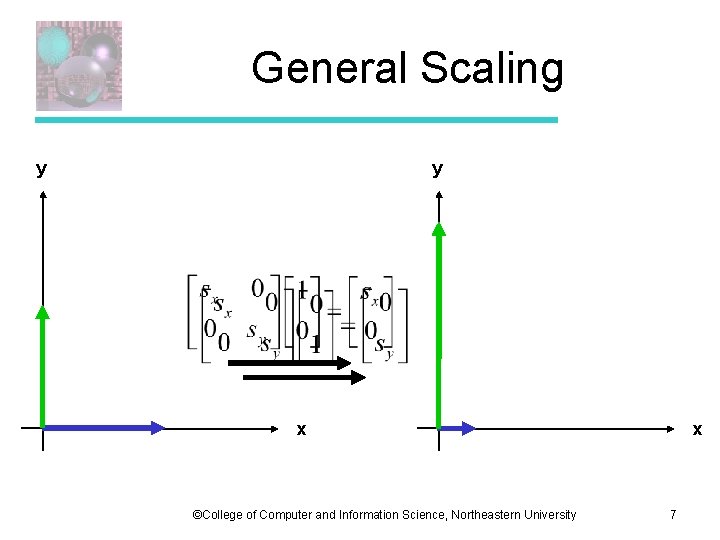
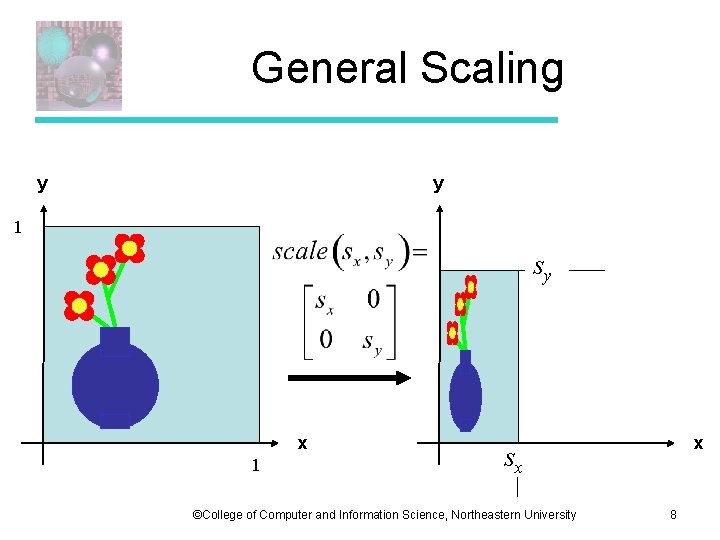
General Scaling y y x ©College of Computer and Information Science, Northeastern University x 7

General Scaling y y 1 sy x 1 x sx ©College of Computer and Information Science, Northeastern University 8

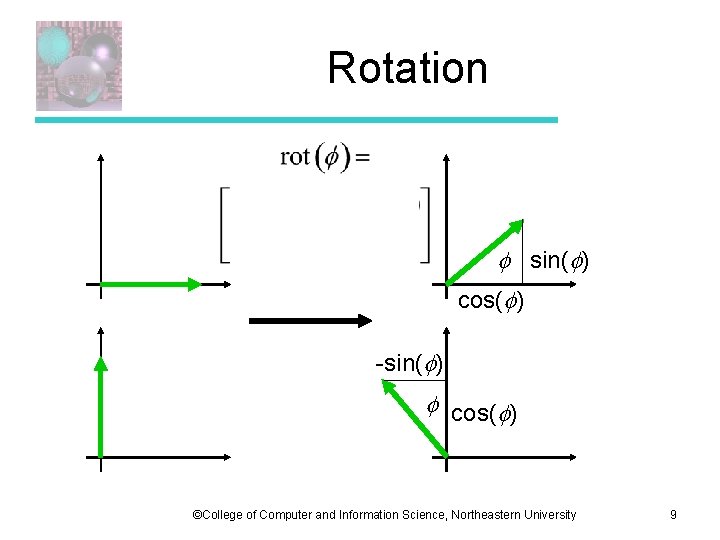
Rotation sin( ) cos( ) -sin( ) cos( ) ©College of Computer and Information Science, Northeastern University 9

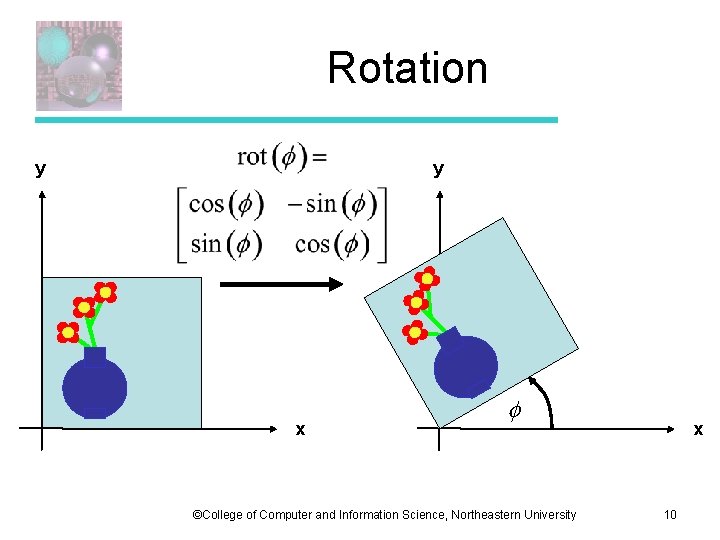
Rotation y y x ©College of Computer and Information Science, Northeastern University x 10

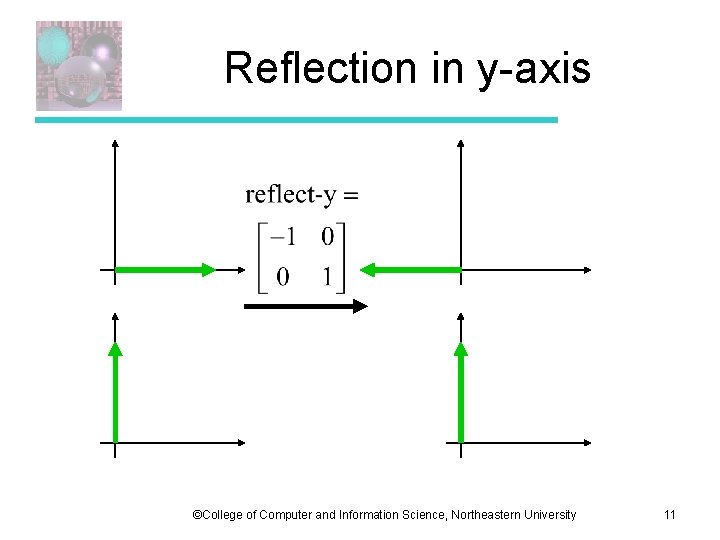
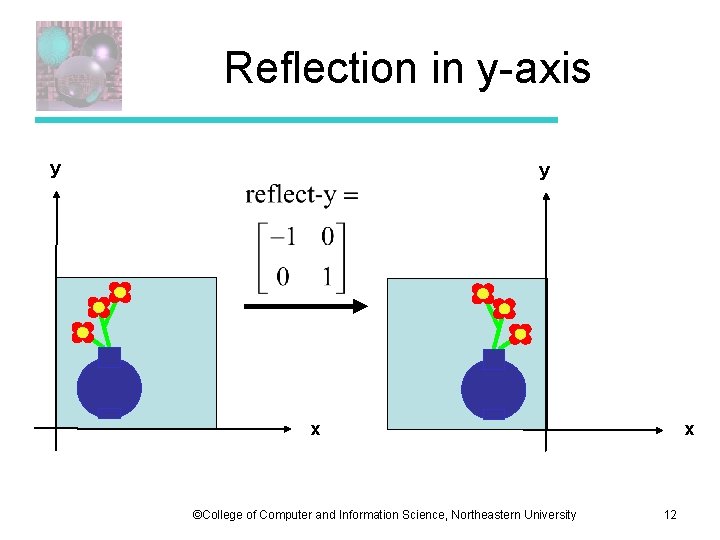
Reflection in y-axis ©College of Computer and Information Science, Northeastern University 11

Reflection in y-axis y y x ©College of Computer and Information Science, Northeastern University x 12

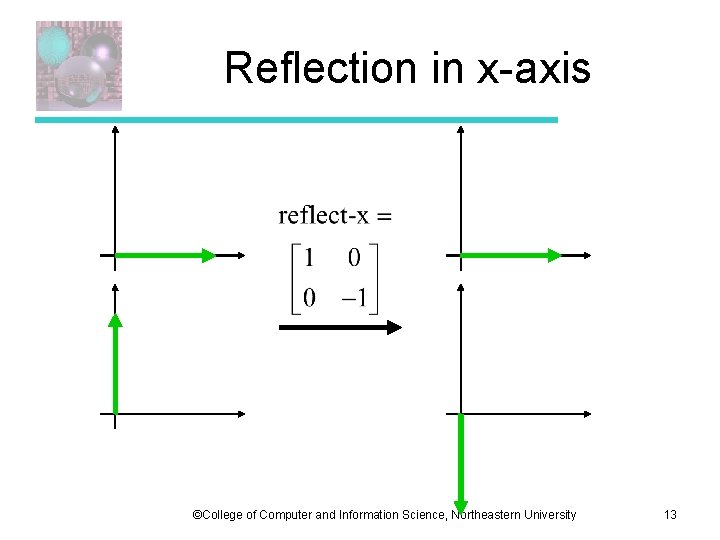
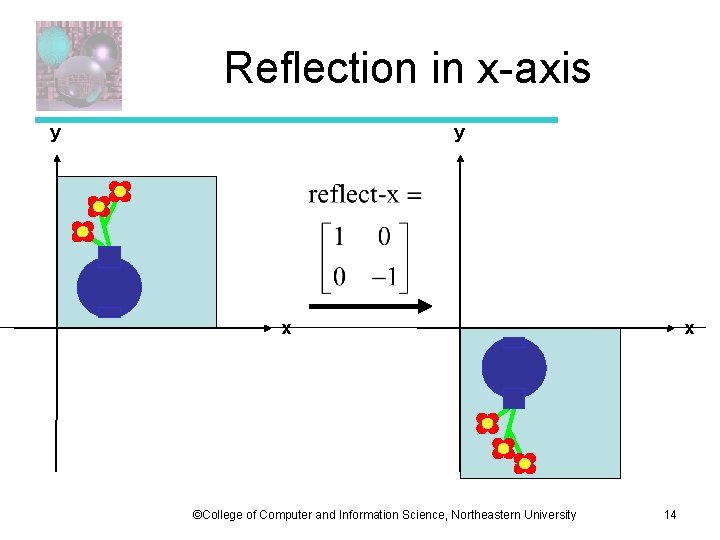
Reflection in x-axis ©College of Computer and Information Science, Northeastern University 13

Reflection in x-axis y y x ©College of Computer and Information Science, Northeastern University x 14

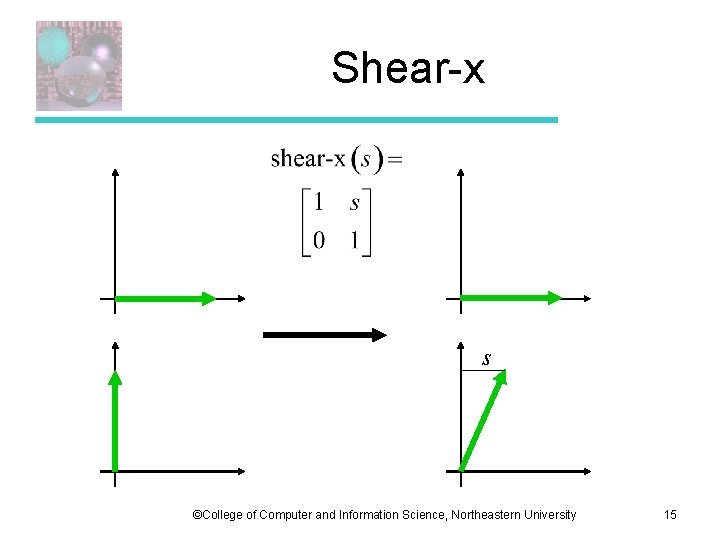
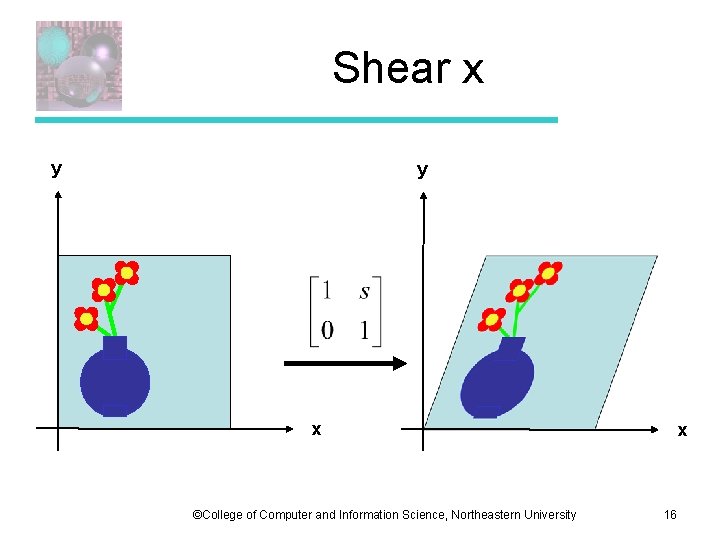
Shear-x s ©College of Computer and Information Science, Northeastern University 15

Shear x y y x ©College of Computer and Information Science, Northeastern University x 16

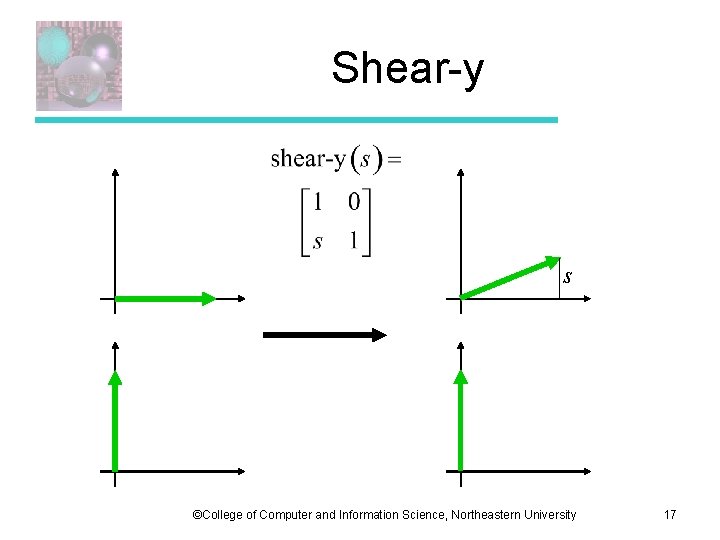
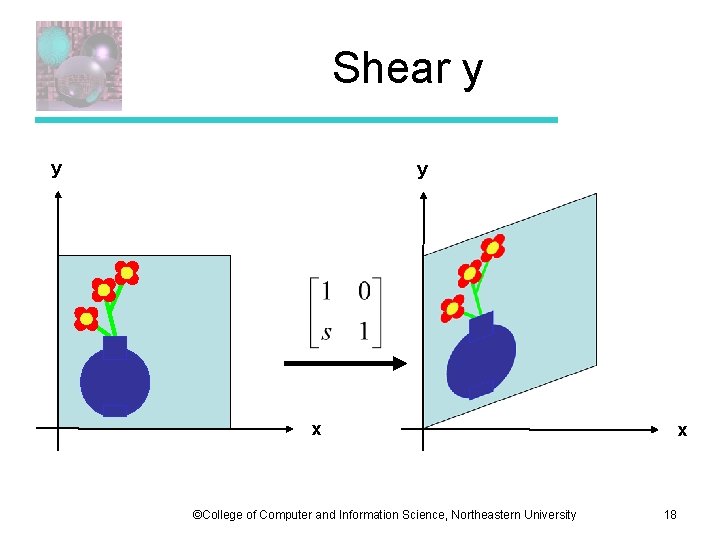
Shear-y s ©College of Computer and Information Science, Northeastern University 17

Shear y y y x ©College of Computer and Information Science, Northeastern University x 18

Linear Transformations • Scale, Reflection, Rotation, and Shear are all linear transformations • They satisfy: T(au + bv) = a. T(u) + b. T(v) § u and v are vectors § a and b are scalars • If T is a linear transformation § T((0, 0)) = (0, 0) ©College of Computer and Information Science, Northeastern University 19

Composing Linear Transformations • If T 1 and T 2 are transformations § T 2 T 1(v) =def T 2( T 1(v)) • If T 1 and T 2 are linear and are represented by matrices M 1 and M 2 § T 2 T 1 is represented by M 2 M 1 § T 2 T 1(v) = T 2( T 1(v)) = (M 2 M 1)(v) ©College of Computer and Information Science, Northeastern University 20

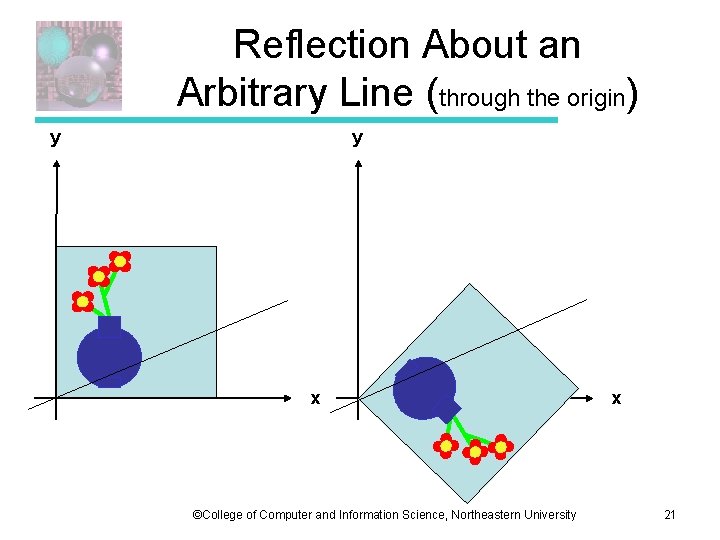
Reflection About an Arbitrary Line (through the origin) y y x ©College of Computer and Information Science, Northeastern University x 21

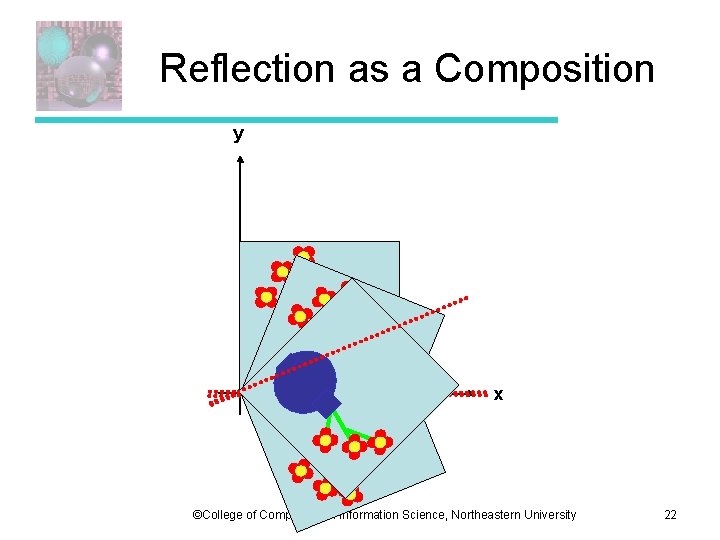
Reflection as a Composition y x ©College of Computer and Information Science, Northeastern University 22

Decomposing Linear Transformations • Any 2 D Linear Transformation can be decomposed into the product of a rotation, a scale, and a rotation if the scale can have negative numbers. • M = R 1 SR 2 ©College of Computer and Information Science, Northeastern University 23

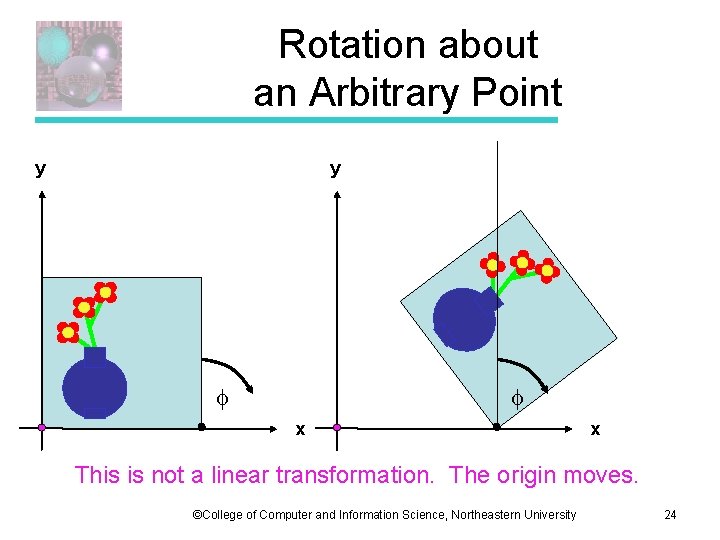
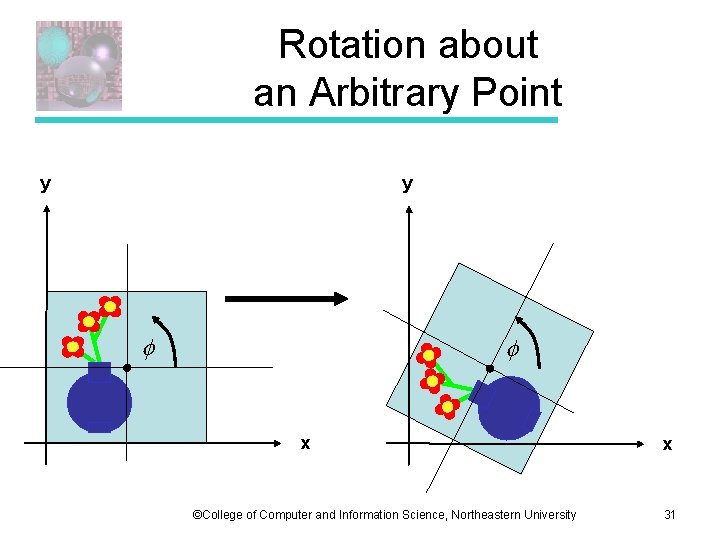
Rotation about an Arbitrary Point y y x x This is not a linear transformation. The origin moves. ©College of Computer and Information Science, Northeastern University 24

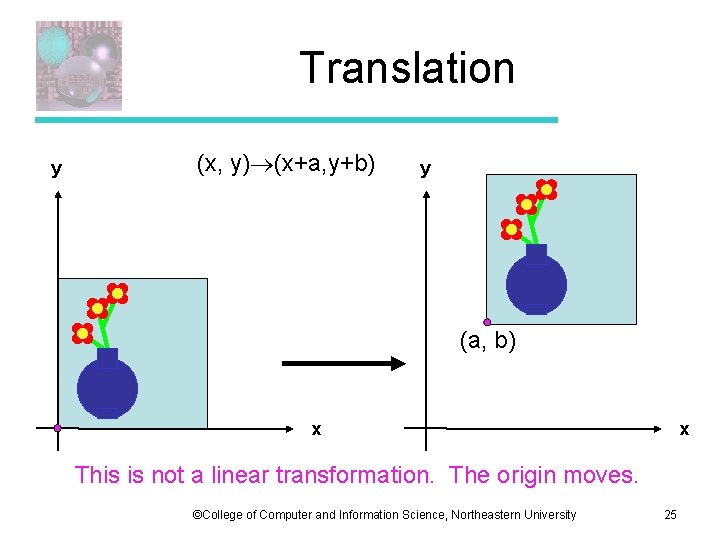
Translation y (x, y) (x+a, y+b) y (a, b) x x This is not a linear transformation. The origin moves. ©College of Computer and Information Science, Northeastern University 25

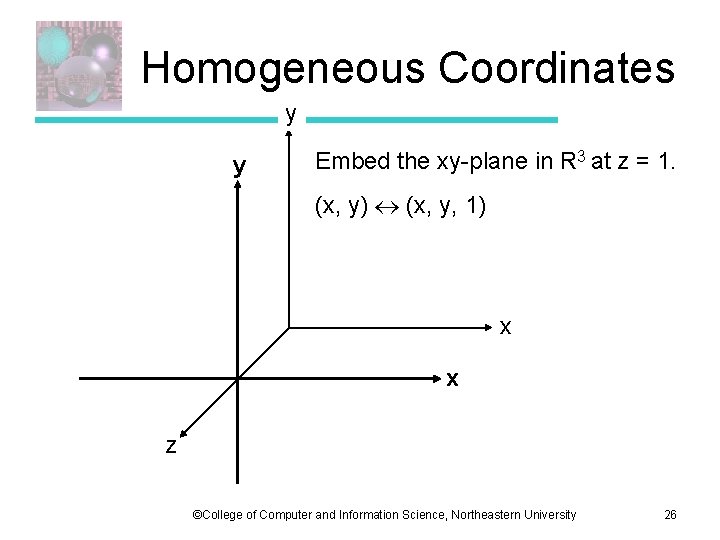
Homogeneous Coordinates y y Embed the xy-plane in R 3 at z = 1. (x, y) (x, y, 1) x x z ©College of Computer and Information Science, Northeastern University 26

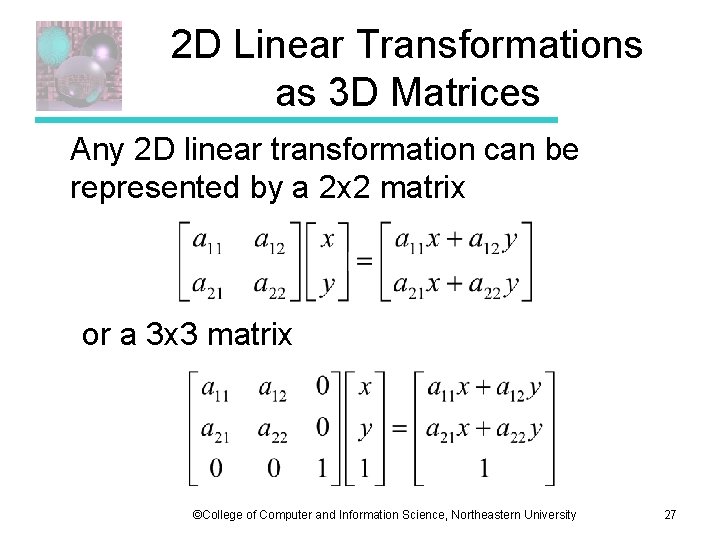
2 D Linear Transformations as 3 D Matrices Any 2 D linear transformation can be represented by a 2 x 2 matrix or a 3 x 3 matrix ©College of Computer and Information Science, Northeastern University 27

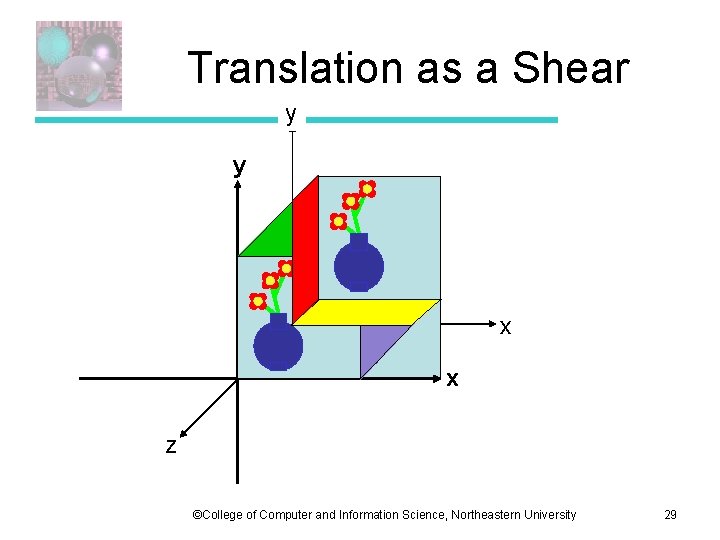
2 D Linear Translations as 3 D Matrices Any 2 D translation can be represented by a 3 x 3 matrix. This is a 3 D shear that acts as a translation on the plane z = 1. ©College of Computer and Information Science, Northeastern University 28

Translation as a Shear y y x x z ©College of Computer and Information Science, Northeastern University 29

2 D Affine Transformations • An affine transformation is any transformation that preserves co-linearity (i. e. , all points lying on a line initially still lie on a line after transformation) and ratios of distances (e. g. , the midpoint of a line segment remains the midpoint after transformation). • With homogeneous coordinates, we can represent all 2 D affine transformations as 3 D linear transformations. • We can then use matrix multiplication to transform objects. ©College of Computer and Information Science, Northeastern University 30

Rotation about an Arbitrary Point y y x ©College of Computer and Information Science, Northeastern University x 31

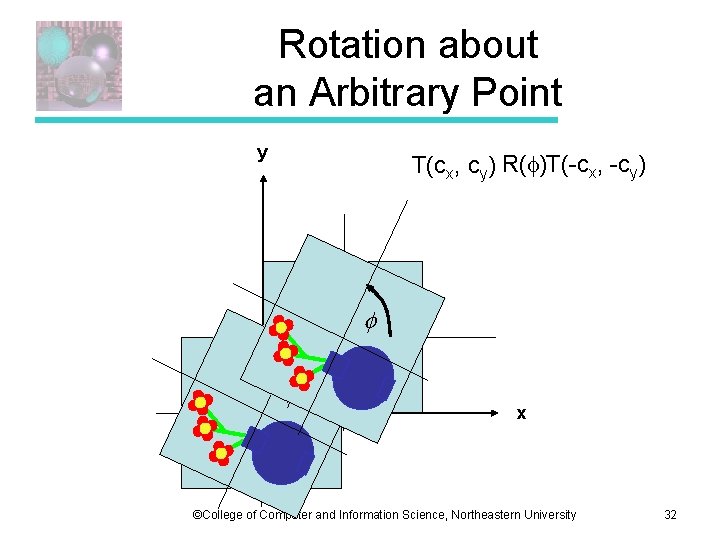
Rotation about an Arbitrary Point y T(cx, cy) R( )T(-cx, -cy) x ©College of Computer and Information Science, Northeastern University 32

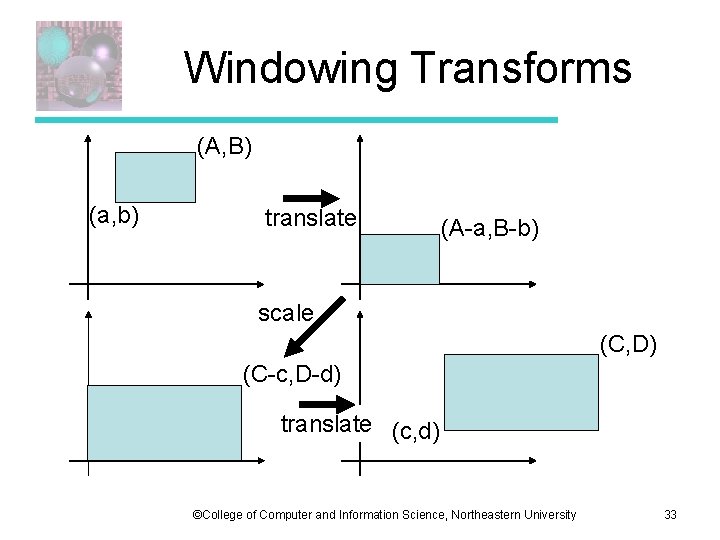
Windowing Transforms (A, B) (a, b) translate (A-a, B-b) scale (C, D) (C-c, D-d) translate (c, d) ©College of Computer and Information Science, Northeastern University 33

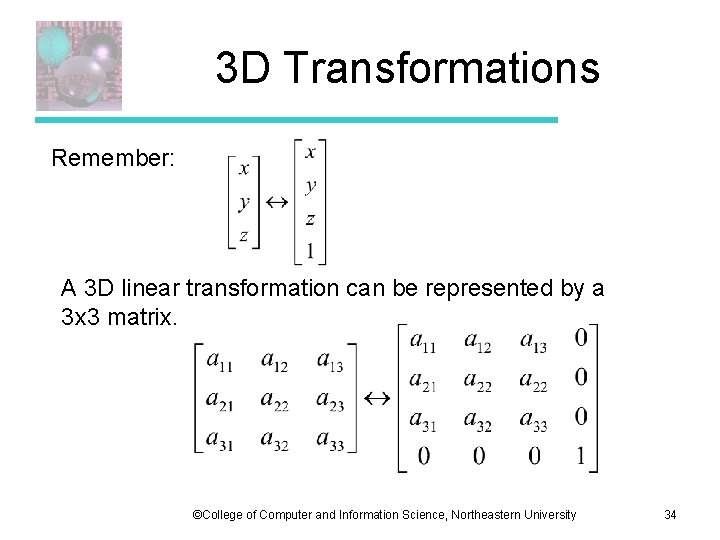
3 D Transformations Remember: A 3 D linear transformation can be represented by a 3 x 3 matrix. ©College of Computer and Information Science, Northeastern University 34

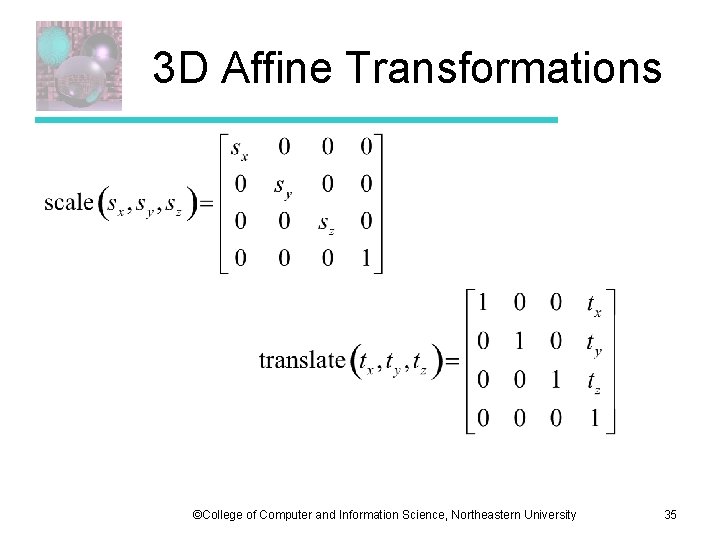
3 D Affine Transformations ©College of Computer and Information Science, Northeastern University 35

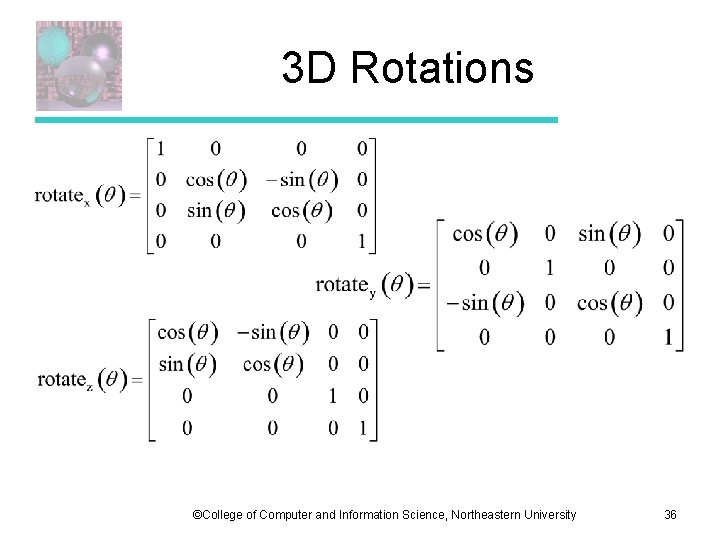
3 D Rotations ©College of Computer and Information Science, Northeastern University 36