CS 655 Computer Graphics The Rendering Equation The

CS 655 – Computer Graphics The Rendering Equation

The Rendering Equation • Developed by Kajiya in 1986 • An attempt to unify rendering so that all rendering has a basic model as a basis • Accounts for all light interactions in an environment

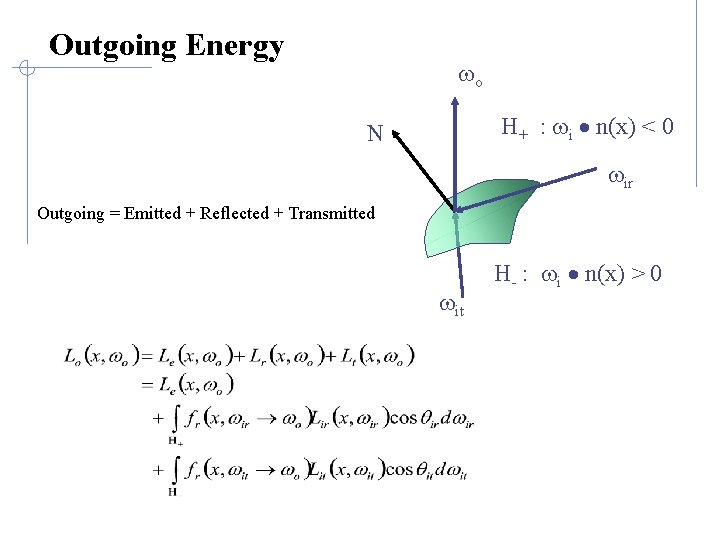
Energy Balance • Outgoing – Incoming = Emitted – Absorbed § The total light energy put into the system must equal the energy leaving the system (usually, via heat). • Outgoing = Emitted + Reflected + Transmitted

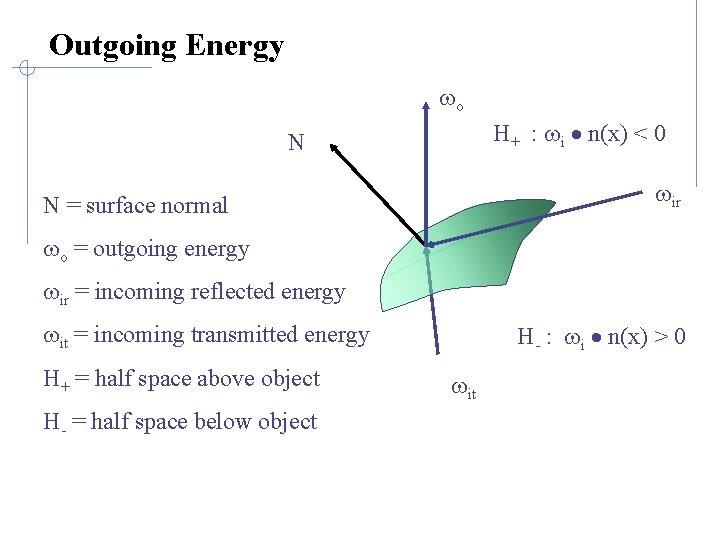
Outgoing Energy wo H+ : wi · n(x) < 0 N wir N = surface normal wo = outgoing energy wir = incoming reflected energy wit = incoming transmitted energy H+ = half space above object H- = half space below object H- : wi · n(x) > 0 wit

Steady State. How come we never notice? How long does it take lighting to stabilize in a 20 x 10 room with a point light in the center of the room? suppose the room has semi-gloss paint which reflects let's say t 0 turn on light 1. 76098 E-08 light hits far corner 4. 81109 E-08 light travels bounces corner to corner 17. 320508 diagonal distance from light (center of ceiling) to corner 983571056 speed of light (ft/sec) 30 diagonal distance from corner to corner 7. 8612 E-08 light travels corner to corner again 1. 09113 E-07 light travels corner to corner again 1. 39614 E-07 light travels corner to corner again 1. 70115 E-07 light travels corner to corner again 2. 00616 E-07 light travels corner to corner again 2. 31118 E-07 light travels corner to corner again 2. 61619 E-07 light travels corner to corner again 2. 9212 E-07 light travels corner to corner again Single bounce time as freq. TV runs at about 60 hz Ears can hear upto 16, 000 Hz 32, 785, 701. 87 32. 8 gigahertz

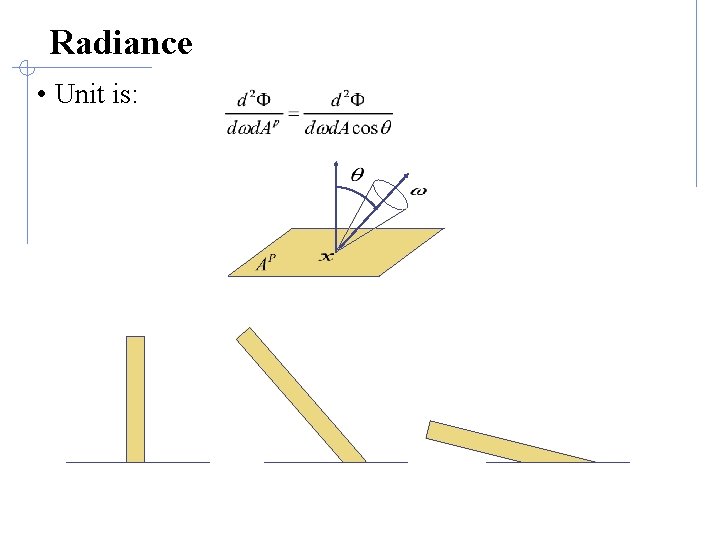
Radiosity vs. Radiance vs. Irradiance vs. Radiant Power • Radiant Power: aka flux, energy flowing to/from a surface per unit time (Watt, aka Joule/sec) • Radiance: exiting power per unit area (Watts/m^2) • Irradiance: incoming power per unit area (Watts/m^2) • Radiosity: exiting power per unit projected area per unit solid angle § § Varies with position and direction. Captures the notion of appearance (for a given location and direction).

Radiance • Unit is:

Basic Equations Radiant power Incident radiant power at x Exitant radiant power at x

BRDF • Bidirectional Reflectance Distribution Function § A measurement of the amount of energy being distributed about all directions from a point.

Diffuse BRDF • Light is reflected equally in all directions

Specular BRDF • Light is reflected only in one direction

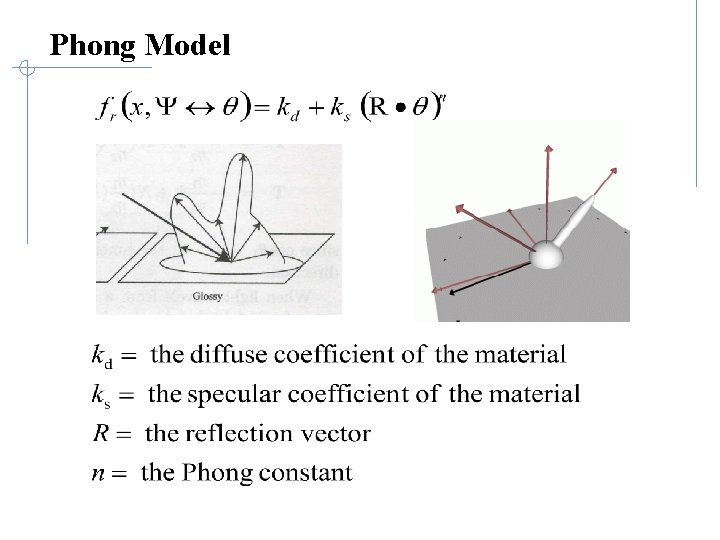
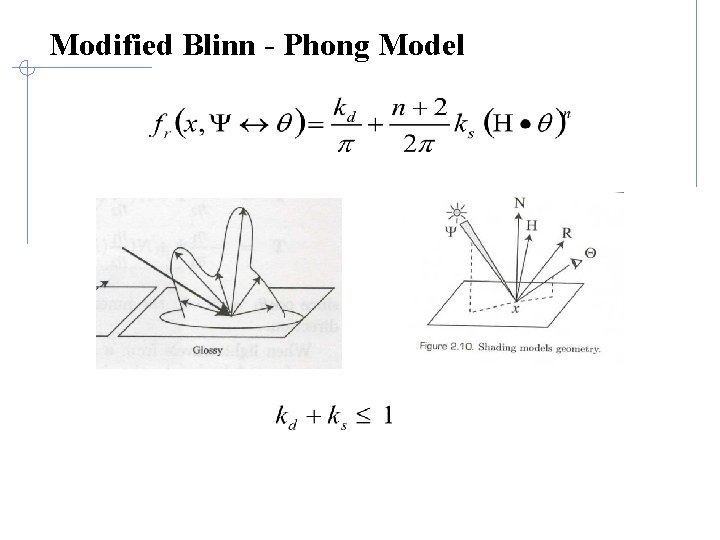
Glossy BRDF • Light is reflected unequally in many directions • Several models exist that attempt to represent glossy BRDFs.

Phong Model

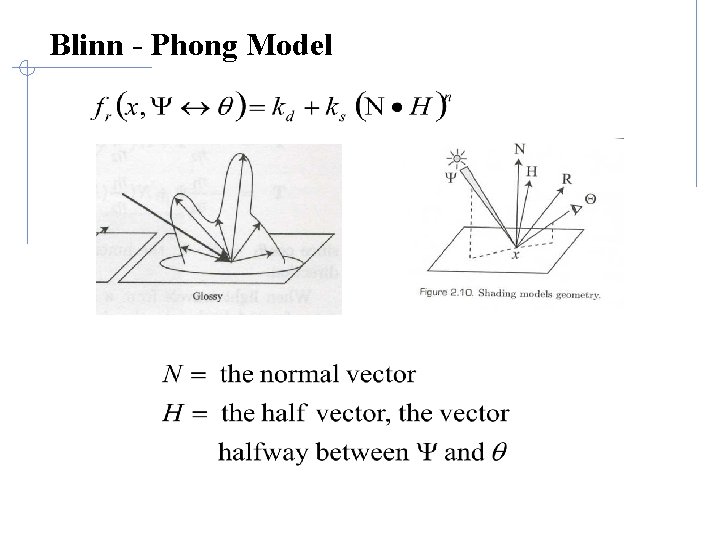
Blinn - Phong Model

Modified Blinn - Phong Model

Outgoing Energy wo H+ : wi · n(x) < 0 N wir Outgoing = Emitted + Reflected + Transmitted wit H- : wi · n(x) > 0

Outgoing Energy Outgoing = Emitted + Reflected + Transmitted

Outgoing Energy Outgoing = Emitted + Reflected + Transmitted

Outgoing Energy N wo H+ H wit - wir

The Rendering Equation Unoccluded two point transfer No participating media If occluded, this is 0 If not occluded, this is the inverse square of the distance between x and x’ Energy emitted from point x’ that reaches point x

The Rendering Equation The intensity of energy originating from x’’, coming through point x’, and terminating at point x The BRDF

The Rendering Equation • In other words, the transport intensity from x’ to x is the sum of the emitted light from x’ that reaches x, plus all of the light from x’’ that eventually gets to x through x’ • We can rewrite the equation as: • Where M is the linear integral operator

Breaking Down the Rendering Equation • Rearranging terms gives:

Breaking Down the Rendering Equation Light to x directly from x’ Light from light source to x’, then to x Light to x via x’ scattered twice Light to x via x’ scattered three times etc.

Applying the Rendering Equation • Local reflection models: • only the first two terms are used • the ge term is non-zero only for light sources • M operates on e rather than g, so shadows are not computed

Applying the Rendering Equation • Basic ray tracing: • Mo is the sum of the reflection and refraction terms • the geo gives shadows, but only for point light sources • Ambient lighting is accounted for in e • M is generally approximated by a small sum