CS 6310 Advanced Data Structures Tree Structures for

OUTLINE Interval Trees � Segment Trees � Trees for the Union of Intervals �

Interval Trees Stores a set of intervals � Returns for any query key all

Interval Trees (Cont. ) If query_key < n_key � we set list to n->left_list

Interval Trees (Cont. ) Every level there is at most one associated node �

Segment Trees Keeping track of a set of n intervals � Performance is worser

Trees for the Union of Intervals It comes with a problem whether it is

Trees for the Union of Intervals Two dimensional measure problems: � � Structure maintaining

Trees for the Union of Intervals We need associated intervals as concept � �

Trees for the Union of Intervals In order to make query easier, we need

Trees for the Union of Intervals � n->transfer // is the pointer to the

Trees for Sums of Weighted Intervals Simple but useful application � Keeps track of

Trees for Sums of Weighted Intervals Some source like electricity � Resource used by

Trees for Sums of Weighted Intervals Easy to built but need extra fields �

Trees for Interval-Restricted Maximum Sum Queries � Same objects, piecewise constant functions or set

Trees for Interval-Restricted Maximum Sum Queries

Trees for Interval-Restricted Maximum Sum Queries Built like Segment Trees � Has additional fields

Slides: 24

Download presentation

CS 6310 Advanced Data Structures Tree Structures for Set of Intervals by Halil Ibrahim DURSUNOGLU

OUTLINE Interval Trees � Segment Trees � Trees for the Union of Intervals � Trees for Sums of Weighted Intervals � Trees for Interval-Restricted Maximum Sum Queries �

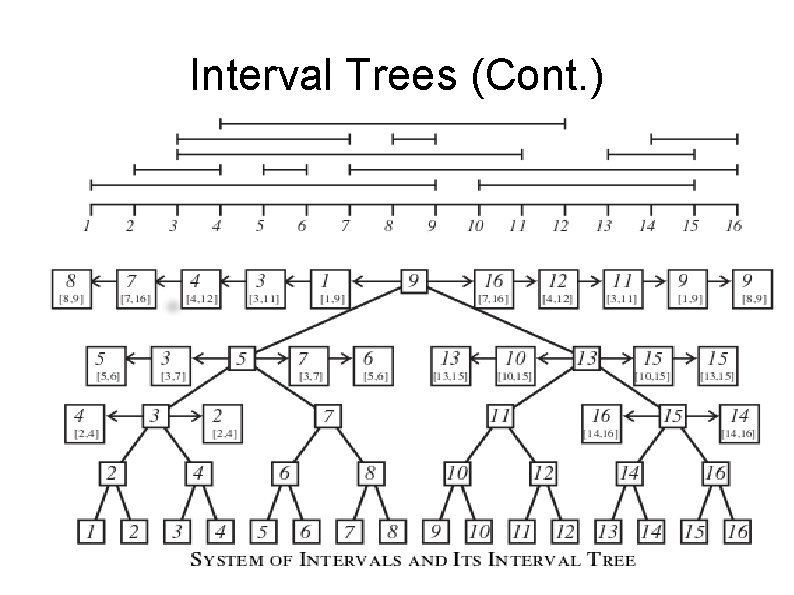
Interval Trees Stores a set of intervals � Returns for any query key all the intervals that contain this query value � Each interval [ai, bi] � � The key of node is contained � The interval is contained in the interrval associated with the node.

Interval Trees (Cont. )

Interval Trees (Cont. ) If query_key < n_key � we set list to n->left_list � while list != NULL and list->key <= query_key � Else query_key >= n->key � we set list to n->right_list � While list!=NULL and list->key >=query_key �

Interval Trees (Cont. ) Every level there is at most one associated node � If query_key < node->key � left endpoint <= query key <= n->key <= right end point � If query_key > node->key � left endpoint <= node->key <= query_key <= right endpoint �

OUTLINE Interval Trees � Segment Trees � Trees for the Union of Intervals � Trees for Sums of Weighted Intervals � Trees for Interval-Restricted Maximum Sum Queries �

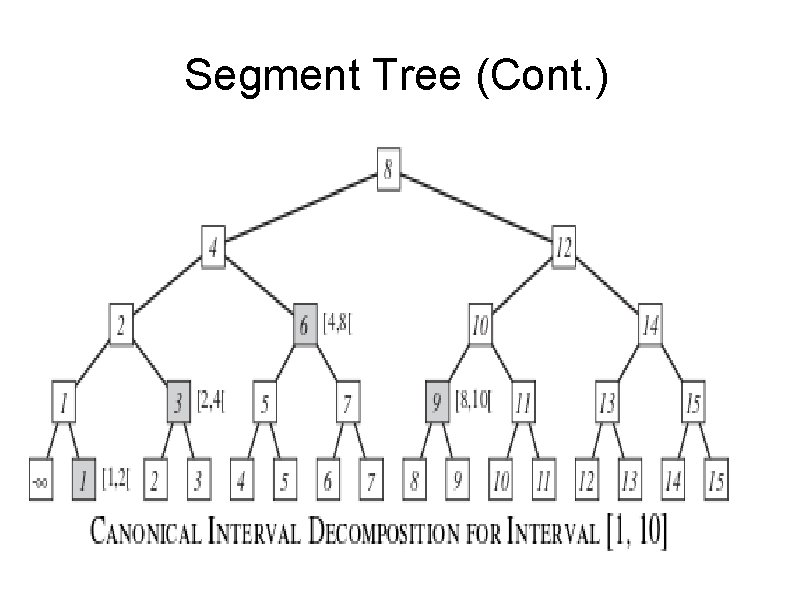
Segment Trees Keeping track of a set of n intervals � Performance is worser than interval tree � A number of more general tasks can be done �

Segment Tree (Cont. )

OUTLINE Interval Trees � Segment Trees � Trees for the Union of Intervals � Trees for Sums of Weighted Intervals � Trees for Interval-Restricted Maximum Sum Queries �

Trees for the Union of Intervals It comes with a problem whether it is possible to determine the measure (length) of a union of n intervals in time better than Theta(n logn). � Simple solution: � � Sort interval endpoints � Sweep from the smallest end point up � Keep track of the number of intervals

Trees for the Union of Intervals Two dimensional measure problems: � � Structure maintaining measure of intervals under insertion and deletion � Each node contains n->measure � if n->interval_list != NULL �n->measure is length of node interval of n � if n is leaf and n->interval_list = NULL �n->measure = 0 � if n is interior and n->interval_list = NULL �n->measure = n->left->measure + n->right->measure

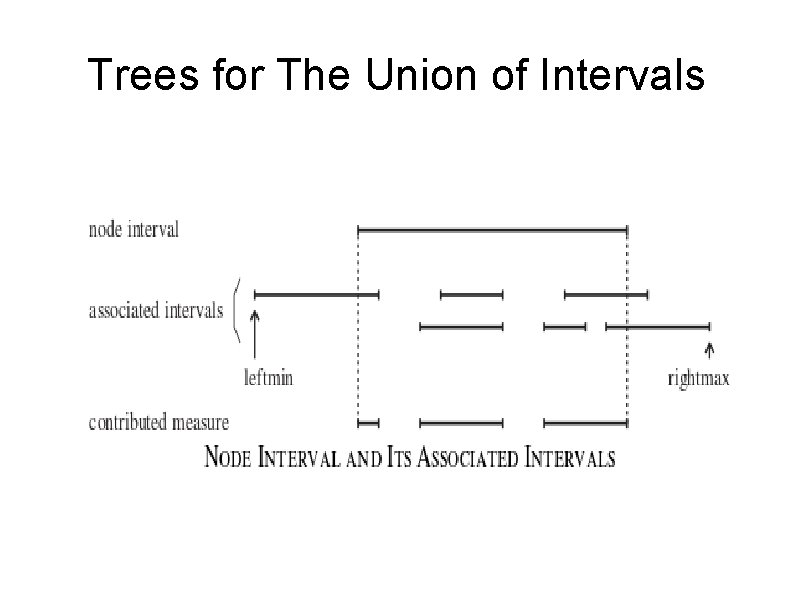
Trees for the Union of Intervals We need associated intervals as concept � � n->measure is the measure of the intersection of the node with the union of all its associated intervals � n->rightmax is the maximum right end point all of interval associated with n � n->leftmin the minimum leftendpoint of all intervals associated with n

Trees for The Union of Intervals

Trees for the Union of Intervals In order to make query easier, we need to some additional fields � � n->leftmin � n->leftmax � n->rigtmin � n->rightmax � n->next // is the pointer to the leaf with next larger key

Trees for the Union of Intervals � n->transfer // is the pointer to the highest node v with � v->left->rightmin = n and � v->left->rightmax->key >= v->key

OUTLINE Interval Trees � Segment Trees � Trees for the Union of Intervals � Trees for Sums of Weighted Intervals � Trees for Interval-Restricted Maximum Sum Queries �

Trees for Sums of Weighted Intervals Simple but useful application � Keeps track of a piecewise constant function �

Trees for Sums of Weighted Intervals Some source like electricity � Resource used by various system � Time interval at a constant level � To construct it, segment tree is used � Ask only for the number of covering intervals �

Trees for Sums of Weighted Intervals Easy to built but need extra fields � n->summand � To insert a weighted interval, firstly insert interval endpoint � �

OUTLINE Interval Trees � Segment Trees � Trees for the Union of Intervals � Trees for Sums of Weighted Intervals � Trees for Interval-Restricted Maximum Sum Queries �

Trees for Interval-Restricted Maximum Sum Queries � Same objects, piecewise constant functions or set of weighted invertal but supporting even stronger queries �

Trees for Interval-Restricted Maximum Sum Queries

Trees for Interval-Restricted Maximum Sum Queries Built like Segment Trees � Has additional fields to Trees for Sums of Weighted Intervals � n->partial_sum � O(logn) �